基于DBN-ELM的聚丙烯熔融指數(shù)的軟測量

王宇紅，狄克松，張姍，尚超，黃德先

?

基于DBN-ELM的聚丙烯熔融指數(shù)的軟測量

王宇紅1，狄克松1，張姍1，尚超2，黃德先2

（1中國石油大學(xué)（華東）信息與控制工程學(xué)院，山東青島 266580；2清華大學(xué)自動化系，北京 100084）

針對聚丙烯熔融指數(shù)軟測量中預(yù)測精度不高的缺點(diǎn)，將基于深度置信網(wǎng)絡(luò)-極限學(xué)習(xí)機(jī)（DBN-ELM）的軟測量方法應(yīng)用到熔融指數(shù)的軟測量中。與傳統(tǒng)深度置信網(wǎng)絡(luò)（DBN）不同的是，該方法將極限學(xué)習(xí)機(jī)（ELM）算法運(yùn)用到深度置信網(wǎng)絡(luò)的訓(xùn)練中。首先用深度置信網(wǎng)絡(luò)對原始數(shù)據(jù)進(jìn)行數(shù)值分析來提取特征，然后將提取的特征輸入到極限學(xué)習(xí)機(jī)中進(jìn)行訓(xùn)練，得到軟測量模型。實(shí)驗(yàn)驗(yàn)證表明，與支持向量機(jī)和單純的深度置信網(wǎng)絡(luò)模型相比，該方法具有更高的測量精度。

深度置信網(wǎng)絡(luò)；算法；極限學(xué)習(xí)機(jī)；數(shù)值分析；特征提取；實(shí)驗(yàn)驗(yàn)證

引 言

熔融指數(shù)是聚丙烯生產(chǎn)過程中一個重要的質(zhì)量指標(biāo)，決定了產(chǎn)品的不同牌號。目前，聚丙烯生產(chǎn)過程中控制產(chǎn)品質(zhì)量的一個主要困難就是沒有對應(yīng)的在線分析儀表。聚丙烯熔融指數(shù)只能通過人工采樣、離線化驗(yàn)分析得到，并且化驗(yàn)周期一般為2～4 h，時間滯后比較大，難以滿足生產(chǎn)質(zhì)量實(shí)時控制的要求，從而導(dǎo)致生產(chǎn)過程的熔融指數(shù)總是處于波動之中，特別是在產(chǎn)品牌號切換過程中會產(chǎn)生大量的不合格產(chǎn)品，帶來很大的經(jīng)濟(jì)損失[1-3]。因此，如果能夠建立實(shí)時反映聚丙烯熔融指數(shù)的軟測量模型，對實(shí)現(xiàn)聚丙烯生產(chǎn)過程的平穩(wěn)操作、提高產(chǎn)品質(zhì)量以及聚丙烯最優(yōu)牌號切換均具有重要的意義[4]。

目前已經(jīng)有很多學(xué)者開展了該領(lǐng)域的研究。文獻(xiàn)[5]提出一種基于支持向量機(jī)的軟測量模型。文獻(xiàn)[6]首次提出將深度學(xué)習(xí)用于軟測量的建模。文獻(xiàn)[7]提出將DBN-ELM用于球磨機(jī)料位的軟測量建模，并取得好的效果。文獻(xiàn)[8]基于生產(chǎn)過程的質(zhì)量平衡和能量平衡建立聚丙烯熔融指數(shù)的預(yù)測模型。文獻(xiàn)[9]針對聚丙烯裝置熔融指數(shù)軟測量中的非線性以及多工況切換問題，提出一種基于卡爾曼濾波-正交最小二乘(Kalman-OLS )的非線性自適應(yīng)軟測量方法。文獻(xiàn)[10]針對聚丙烯生產(chǎn)過程的非線性，提出了一種基于KPCA和組合神經(jīng)網(wǎng)絡(luò)的軟測量方法。文獻(xiàn)[11-12]提出一種模糊技術(shù)與人工神經(jīng)網(wǎng)絡(luò)或支持向量機(jī)的組合模型。文獻(xiàn)[13-14]提出一種混合群智能算法與RBFNN或SVM的組合模型。在聚丙烯的軟測量方面盡管取得了很多的研究成果，但是目前研究工作仍然存在著模型復(fù)雜或預(yù)測精度不高等不足。

最近神經(jīng)網(wǎng)絡(luò)研究成果表明，深度置信網(wǎng)絡(luò)（deep belief network, DBN）作為一種深層神經(jīng)網(wǎng)絡(luò)，具有良好的特征學(xué)習(xí)能力，通過對低層特征的組合形成更加抽象的高層表示，使分類或預(yù)測更容易[15]。另外，DBN在時間序列的預(yù)測方面也有成功的應(yīng)用[16]。在DBN的訓(xùn)練過程中，首先通過無監(jiān)督貪婪訓(xùn)練每一層RBM，將訓(xùn)練后的RBM組合構(gòu)建DBN，然后采用傳統(tǒng)的全局優(yōu)化算法對整個網(wǎng)絡(luò)進(jìn)行微調(diào)，使網(wǎng)絡(luò)達(dá)到最優(yōu)。然而基于梯度的全局優(yōu)化算法會陷入局部最優(yōu)，并不能很好地訓(xùn)練深層神經(jīng)網(wǎng)絡(luò)，并且這樣的全局微調(diào)需要大量的訓(xùn)練時間。因此，將極限學(xué)習(xí)機(jī)算法運(yùn)用到DBN的訓(xùn)練過程中，對DBN進(jìn)行改進(jìn)來改善DBN的性能，提高模型的預(yù)測準(zhǔn)確率。

綜上所述，本文將DBN與ELM相結(jié)合用于聚丙烯熔融指數(shù)的軟測量。實(shí)驗(yàn)結(jié)果表明，相比傳統(tǒng)軟測量方法，該方法具有更高的預(yù)測精度，為聚丙烯熔融指數(shù)軟測量的研究和應(yīng)用提供了新的方法。

1 深度置信網(wǎng)絡(luò)

深度置信網(wǎng)絡(luò)（DBN）作為一種多層網(wǎng)絡(luò)，近來受到廣泛的關(guān)注[17]。對于多層神經(jīng)網(wǎng)絡(luò)來說，單純地采用梯度下降訓(xùn)練很難達(dá)到較好的效果，深度置信網(wǎng)絡(luò)采用深度學(xué)習(xí)算法很好地解決了該問題。深度學(xué)習(xí)算法由兩個階段組成，即無監(jiān)督的預(yù)訓(xùn)練階段和有監(jiān)督的反向傳播階段。在無監(jiān)督的預(yù)訓(xùn)練階段，DBN首先被預(yù)訓(xùn)練作為有監(jiān)督階段的初始權(quán)重；在有監(jiān)督的反向傳播階段，對整個網(wǎng)絡(luò)進(jìn)行調(diào)優(yōu)。

DBN可看作通過疊加若干層受限玻爾茲曼機(jī)（restricted Boltzmann machine, RBM）分級建立而成，如圖1所示。每一層可以看作一個單獨(dú)的RBM。RBM是一種兩層神經(jīng)網(wǎng)絡(luò)，由一層代表輸入的可見層和一層代表隱變量的隱層組成，并且隱變量作為下一個RBM的輸入。DBN采用一種貪婪的逐層訓(xùn)練方法。在圖1中，RBM1首先被訓(xùn)練，并且RBM1的隱層作為RBM2的輸入，然后RBM2被訓(xùn)練，RBM3也以同樣的方式訓(xùn)練。在每一個RBM的訓(xùn)練過程中，隱變量作為特征被從輸入數(shù)據(jù)中提取出來。

相比于傳統(tǒng)的軟測量建模方法，深度置信網(wǎng)絡(luò)一個很大的優(yōu)勢就是快速采樣的過程數(shù)據(jù)可以被充分利用。在工業(yè)過程中，過程變量的采樣速率比質(zhì)量變量的采樣速率要大得多，如圖2所示。結(jié)果，質(zhì)量樣本的數(shù)目要遠(yuǎn)遠(yuǎn)小于過程樣本的數(shù)目。傳統(tǒng)軟測量建模方法只利用了和質(zhì)量變量相同數(shù)目的過程樣本，那些沒有被利用的過程樣本仍然包含豐富的信息。在深度學(xué)習(xí)的過程中，那些沒有被利用的過程變量可以用于非監(jiān)督的預(yù)訓(xùn)練來提取隱變量，有利于促進(jìn)監(jiān)督階段的反向傳播。利用的數(shù)據(jù)越多，挖掘的信息也就越多，建立的模型也就越準(zhǔn)確。因此，采用了深度學(xué)習(xí)算法的深度置信網(wǎng)絡(luò)非常適合用于建立軟測量模型。

2 受限玻爾茲曼機(jī)RBM

2.1 RBM的基本模型

RBM可視為一個無向圖模型，RBM中的可見單元和隱單元可以為任意指數(shù)族單元，如sotfmax單元、高斯單元等[17]。為了方便起見，假設(shè)所有可見單元和隱單元均為二值變量。

假設(shè)一個RBM有個可見單元和個隱單元，和分別代表可見單元和隱單元的狀態(tài)。作為一個系統(tǒng)，當(dāng)給定狀態(tài)（,）時，所具有的能量可表示為[18]

(,)=-T-T-T(1)

其中，為可見層的偏置，為隱層的偏置，為可見層和隱層的連接權(quán)重。

當(dāng)參數(shù)={,,}確定以后，系統(tǒng)的聯(lián)合概率分布可表示為

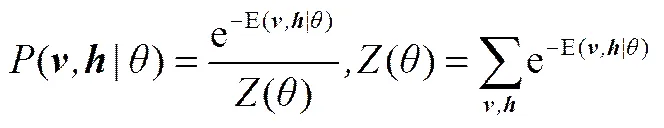
其中，()為歸一化因子。

對于一個實(shí)際問題，主要關(guān)心的是輸入數(shù)據(jù)的分布(|),也稱為對數(shù)似然函數(shù)，即

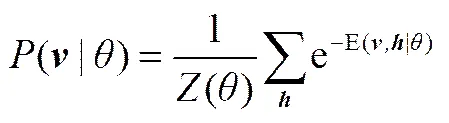
為了確定該分布，需要計(jì)算()，需計(jì)算2+m次，計(jì)算量比較大，因此()比較難計(jì)算。

但是由RBM的特殊結(jié)構(gòu)可知，同層節(jié)點(diǎn)之間的狀態(tài)是相互獨(dú)立的。當(dāng)給定可見節(jié)點(diǎn)的狀態(tài)時，第個隱層節(jié)點(diǎn)的激活概率為

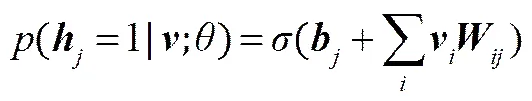
由于RBM的對稱結(jié)構(gòu)，求得隱層節(jié)點(diǎn)后，可見節(jié)點(diǎn)的激活概率為

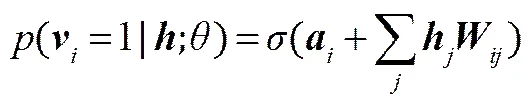
2.2 基于對比散度的RBM訓(xùn)練算法

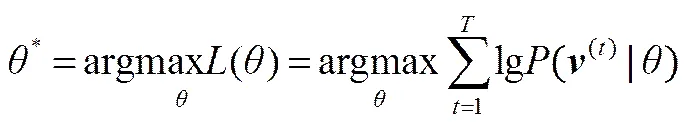
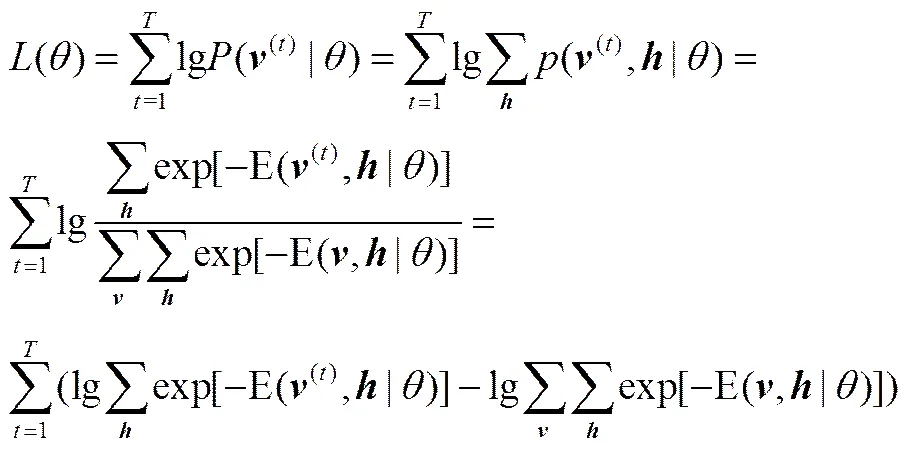
對數(shù)似然函數(shù)關(guān)于參數(shù)的梯度為

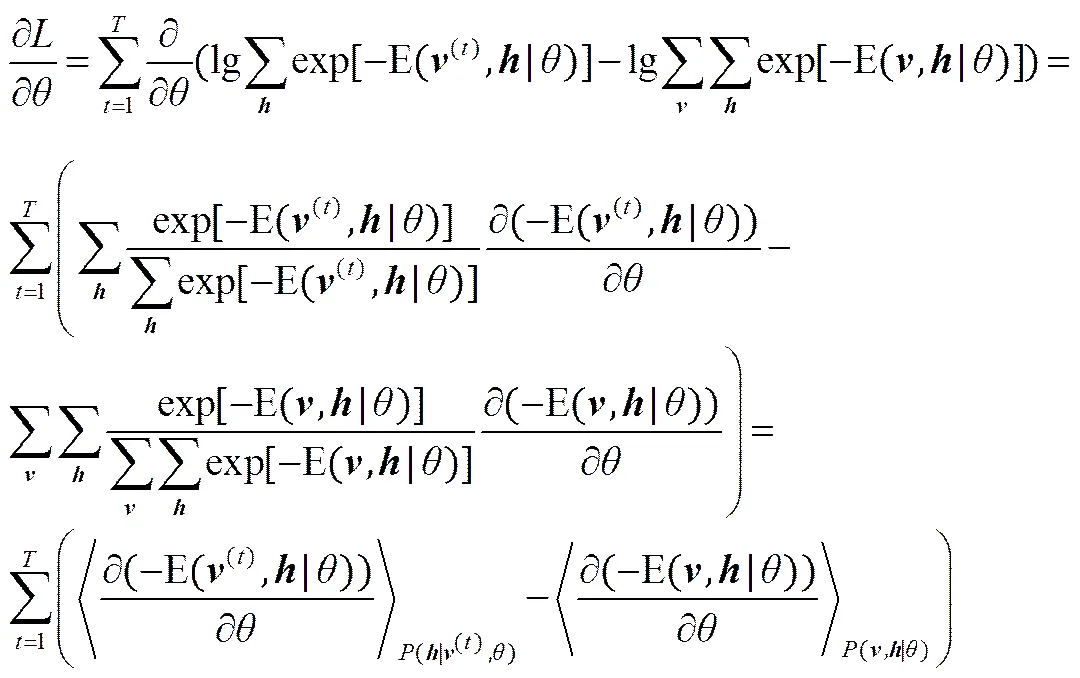
設(shè)表示輸入數(shù)據(jù)，代表隱層向量，代表可見層向量，代表學(xué)習(xí)速率，代表RBM的權(quán)重矩陣，代表輸入層偏置向量，代表輸出層偏置向量。

（1）隨機(jī)初始化模型參數(shù)，并設(shè)定迭代次數(shù)Step。

（2）將原始數(shù)據(jù)賦給可見層向量。

（3）根據(jù)下面兩個公式計(jì)算0、1、1的狀態(tài)值，即隱層和可見層的激活概率為

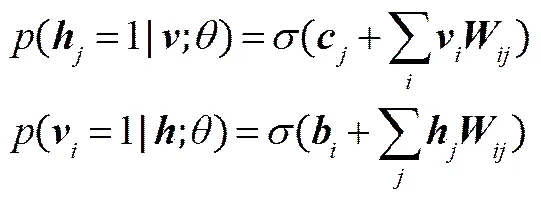
（4）用式（9）對參數(shù)進(jìn)行更新

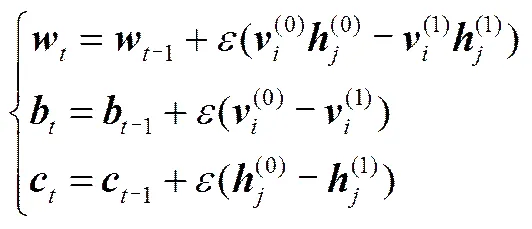
（5）若≥Step，則訓(xùn)練結(jié)束，否則-1將賦給。并轉(zhuǎn)到步驟（3），重新訓(xùn)練。

3 極限學(xué)習(xí)機(jī)ELM

極限學(xué)習(xí)機(jī)是一種適用于單隱層神經(jīng)網(wǎng)絡(luò)的快速學(xué)習(xí)算法。當(dāng)輸入權(quán)重和偏置隨機(jī)初始化以后，輸出權(quán)重也就確定了。

設(shè)一個單隱層神經(jīng)網(wǎng)絡(luò)有個樣本（,t），,。假設(shè)一個單隱層神經(jīng)網(wǎng)絡(luò)有個隱層節(jié)點(diǎn)，則此網(wǎng)絡(luò)可表示為

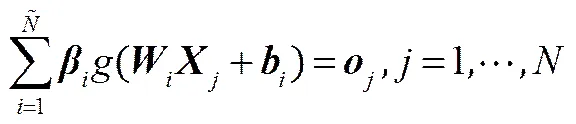
式中，()為激活函數(shù)；=[,1,,2,…,,n]T為輸入權(quán)重；為輸出權(quán)重；為第個隱單元的偏置。

訓(xùn)練單隱層神經(jīng)網(wǎng)絡(luò)的目的是使輸出誤差最小，即

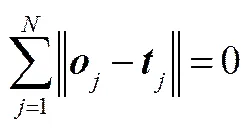
也就是存在特殊的、、，使

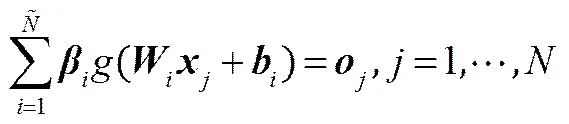
式（12）可以表示為

=

其中，為隱層節(jié)點(diǎn)的輸出；為輸出權(quán)重；為期望輸出。

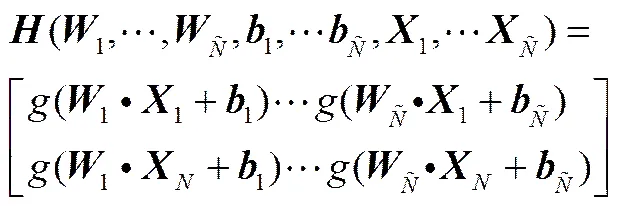
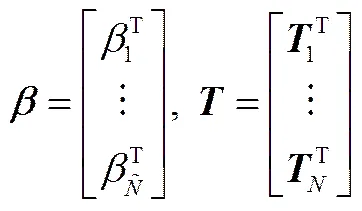
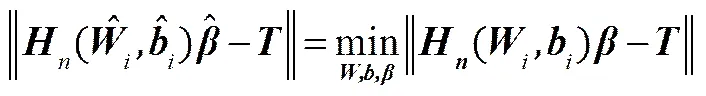
當(dāng)采用ELM算法時，輸入權(quán)重和隱層偏置被隨機(jī)確定后，隱層的輸出矩陣也就確定。此時單隱層神經(jīng)網(wǎng)絡(luò)的訓(xùn)練問題變?yōu)橐粋€線性系統(tǒng)=，輸出權(quán)重即為

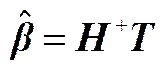
式中，+為矩陣的Moore-Penrose廣義逆。同時，求得的解是最小且唯一。

4 基于DBN的ELM算法

設(shè)一個DBN含有層隱層，通過貪婪的訓(xùn)練方式得到-1個RBM，從輸入層，隱層1，…，隱層-1。而第-1個隱層到第層隱層以及第層隱層到輸出層的權(quán)重和偏置則是由ELM算法確定[20]，改進(jìn)的深度置信網(wǎng)絡(luò)結(jié)構(gòu)如圖3所示。

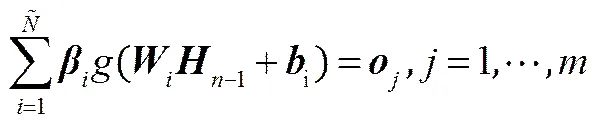
式中，為第-1層隱藏層到第層隱藏層的權(quán)重，為第-1層隱藏層到第層隱藏層的偏置，為第層隱藏層到輸出層的輸出權(quán)重。對于整個網(wǎng)絡(luò)結(jié)構(gòu)來說，目標(biāo)是最小化輸出誤差，可表示為

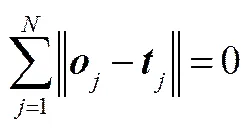
并且存在，使

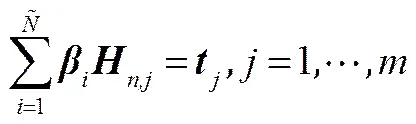
此問題可轉(zhuǎn)化為=。

其中，為DBN第-1層到第層的輸出

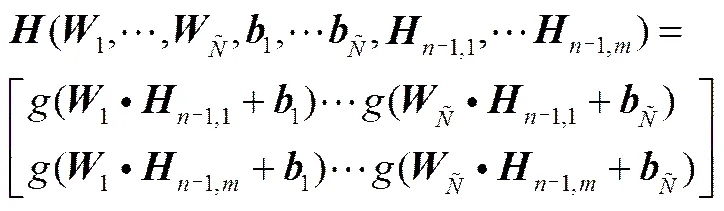
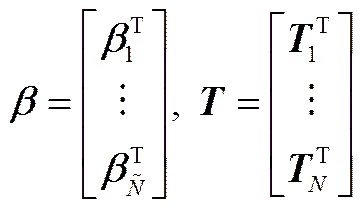
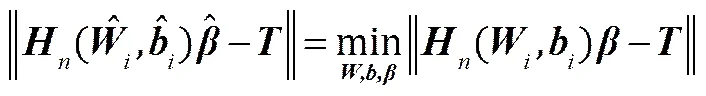
隨機(jī)初始化第-1層隱藏層到第層隱藏層的權(quán)重和偏置，則可以得到隱藏層唯一的輸出矩陣。將深度置信網(wǎng)絡(luò)的訓(xùn)練問題轉(zhuǎn)化成求解線性系統(tǒng)=。同時輸出權(quán)重可被確定為

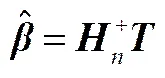
式中，+為矩陣的Moore-Penrose廣義逆。Huang等[21]已經(jīng)證明求得的解最小且唯一。

5 應(yīng)用分析

從現(xiàn)場聚丙烯裝置采集工業(yè)數(shù)據(jù)獲得軟測量所需要的輔助變量，同時從化驗(yàn)車間獲取熔融指數(shù)的化驗(yàn)值,經(jīng)過一系列數(shù)據(jù)預(yù)處理后，最后獲得444組數(shù)據(jù)，將這些數(shù)據(jù)分為兩部分，280組數(shù)據(jù)用于建立軟測量模型，剩余164組數(shù)據(jù)用于模型驗(yàn)證。

本文分別采用SVM、DBN、DBN-ELM的方法建立聚丙烯熔融指數(shù)的軟測量模型，比較不同方法所建立模型的預(yù)測效果，其中，DBN和DBN-ELM的網(wǎng)絡(luò)結(jié)構(gòu)參數(shù)通過交叉驗(yàn)證的方式確定。

3種建模方法所建立模型的預(yù)測結(jié)果列于表1以及圖4～圖6。

表1 3種軟測量建模方法預(yù)測結(jié)果的對比

從表中可以看出，與SVM方法相比，基于DBN所建立的軟測量模型在測試誤差方面，提高并不是很明顯，但是將DBN與ELM結(jié)合后，所建立的基于DBN-ELM的軟測量模型，測試誤差降低了15%。與SVM相比，雖然在訓(xùn)練誤差方面，準(zhǔn)確度有所下降，但是在測試誤差方面，準(zhǔn)確度有了明顯的提高。從軟測量的意義上來說，測試誤差更為重要，有時為了保證較低的測試誤差，有意將訓(xùn)練誤差調(diào)得高一些，使模型的預(yù)測性能更好。因此，總的來說，基于DBN-ELM的軟測量方法具有更高的預(yù)測精度，要優(yōu)于SVM和單獨(dú)的DBN。

6 結(jié) 論

針對聚丙烯熔融指數(shù)難以在線測量的特點(diǎn)以及傳統(tǒng)軟測量方法所存在的預(yù)測精度不足，將DBN-ELM應(yīng)用在聚丙烯熔融指數(shù)的軟測量上。研究結(jié)果表明，基于DBN-ELM所建立的軟測量模型具有更高的預(yù)測精度，有利于過程質(zhì)量的監(jiān)控和先進(jìn)控制的實(shí)施，在聚丙烯生產(chǎn)過程中具有廣闊的應(yīng)用前景。

[1] YI H S, AND J H K, HAN C,. Plantwide optimal grade transition for an industrial high-density polyethylene plant[J]. Industrial & Engineering Chemistry Research, 2003, 42(1): 91-98.

[2] AND F T, BIEGLER L T, SALDíVARGUERRA E. Optimal grade transitions in the high-impact polystyrene polymerization process[J]. Industrial & Engineering Chemistry Research, 2006, 45(18): 6175-6189.

[3] SHARMIN R, SUNDARARAJ U, SHAH S,. Inferential sensors for estimation of polymer quality parameters: industrial application of a PLS-based soft sensor for a LDPE plant[J]. Chemical Engineering Science, 2006, 61(19): 6372-6384.

[4] WEI Y J, JIANG Y H, YAN F,Three-stage decomposition modeling for quality of gas-phase polyethylene process based on adaptive hinging hyperplanes and impulse response template[J]Ind. Eng. Chem. Res., 2013, 52(16): 5747-5756.

[5] 馬勇,黃德先,金以慧.基于支持向量機(jī)的軟測量建模方法[J].信息與控制, 2004, 33(4): 417-421. MA Y, HUANG D X, JIN Y H. Soft-sensor modeling method based on support vector machine[J]. Information and Control, 2004, 33(4): 417-421.

[6] SHANG C, YANG F, HUANG D,. Data-driven soft sensor development based on deep learning technique[J]. Journal of Process Control, 2014, 24(3): 223-233.

[7] 康巖,盧慕超,閻高偉.基于DBN-ELM的球磨機(jī)料位軟測量方法研究[J].儀表技術(shù)與傳感器,2015, (4): 73-75. KANG Y, LU M C, YAN G W. Soft sensor for ball mill fill level based on DBN-ELM model[J]. Instrument Technique and Sensor, 2015, (4): 73-75.

[8] 王平,田華閣,田學(xué)民. Spheripol-Ⅱ雙環(huán)管聚丙烯裝置動態(tài)建模[J].計(jì)算機(jī)與應(yīng)用化學(xué),2008, 25(7): 827-831. WANG P, TIAN H G, TIAN X M. Dynamic modeling of Spheripol-Ⅱ propylene polymerization in dual-loop reactor [J]. Computers and Applied Chemistry, 2008, 25(7): 827-831.

[9] 田華閣,田學(xué)民,鄧曉剛.基于Kalman-OLS的聚丙烯熔融指數(shù)軟測量[J].控制工程,2010, (S1): 83-86. TIAN H G, TIAN X M, DENG X G. Polypropylene melt index soft sensor based on Kalman-Orthogonal least squares[J]. Control Engineering of China, 2010, (S1): 83-86.

[10] 潘澤林,夏陸岳,周猛飛,等. KPCA-SNNs的聚丙烯熔融指數(shù)軟測量[J].計(jì)算機(jī)與應(yīng)用化學(xué),2014, 31(2): 203-206. PAN Z L, XIA L Y, ZHOU M F,. Soft sensor of polypropylene melt index based on KPCA-SNNs[J]. Computers and Applied Chemistry, 2014, 31(2): 203-206.

[11] LIU X, ZHAO C. Melt index prediction based on fuzzy neural networks and PSO algorithm with online correction strategy- s[J]. AIChE Journal, 2012, 58(4): 1194-1202.

[12] ZHANG M, LIU X.A soft sensor based on adaptive fuzzy neural network and support vector regression for industrial melt index prediction[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 126(15): 83-90.

[13] LI J, LIU X, JIANG H,. Melt index prediction by adaptively aggregated RBF neural networks trained with novel ACO algorithm [J]. Journal of Applied Polymer Science, 2012, 125 (2): 829-1656.

[14] 蔣華琴,劉興高.免疫 PSO_WLSSVM最優(yōu)聚丙烯熔融指數(shù)預(yù)報[J]. 化工學(xué)報,2012, 63(3): 866-872. JIANG H Q, LIU X G. Optimal melt index prediction based on ICPSO_WLSSVM algorithm for industrial propylene polymerization[J]. CIESC Journal, 2012, 63(3): 866-872.

[15] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.

[16] LANGKVIST M, KARLSSON L, LOUTFI A.A review of unsupervised feature learning and deep learning for time series modeling[J]. Pattern Recognition Letters, 2014, 42(1): 11-24.

[17] HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J].Neural Computation, 2006, 18(7): 1 527-1554.

[18] 張春霞,姬楠楠,王冠偉.受限波爾茲曼機(jī)[J]. 工程數(shù)學(xué)學(xué)報,2015, (2): 159-173. ZHANG C X, JI N N, WANG G W. Restricted Boltzmann machines[J]. Chinese Journal of Engineering Mathematics, 2015, (2): 159-173.

[19] HUANG G B, ZHOU H, DING X,. Extreme learning maching for regression and multiclass classification[J]. IEEE, Transactions on System, Man, and Cybernetics, 2012, 42(2): 513-529.

[20] 趙志勇,李元香,喻飛,等.基于極限學(xué)習(xí)的深度學(xué)習(xí)算法[J]. 計(jì)算機(jī)工程與設(shè)計(jì), 2015, (4): 1022-1026. ZHAO Z Y, LI Y X, YU F,. Improved deep learning algorithm based on extreme learning machine[J]. Computer Engineering and Design, 2015, (4): 1022-1026.

[21] HUANG G B, ZHOU H, DING X,. Extreme learning machine for regression and multiclass classification.[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2012, 42(42): 513-529.

Melt index prediction of polypropylene based on DBN-ELM

WANG Yuhong1, DI Kesong1, ZHANG Shan1, SHANG Chao2, HUANG Dexian2

(1College of Information and Control Engineering, China University of Petroleum, Qingdao 266580, Shandong, China; 2Department of Automation, Tsinghua University, Beijing 100084, China)

To solve the issue of low accuracy of the traditional soft sensor methods of polypropylene melt index, an approach based on deep belief network and extreme learning machine（DBN-ELM）was used to the melt index prediction of polypropylene. Traditional deep belief network (DBN) applied the deep learning to the learning process of the deep neural networks. Different from traditional deep belief network, this approach applied the extreme learning machine algorithm (ELM) to the learning process of DBN to improve the DBN model. Firstly, deep belief network was employed to extract effective features from vibration data by numerical analysis. Then, the effective features were put into the extreme learning machine to proceed model training to obtain the soft sensor model. The experimental validation showed that the method was more accuracy than the traditional method.

deep belief network; algorithm; extreme learning machine; numerical analysis; feature extraction; experimental validation

date: 2016-09-12.

Prof. WANG Yuhong, Y.H.Wang@upc.edu.cn

10.11949/j.issn.0438-1157.20161280

TP 273

A

0438—1157（2016）12—5163—06

山東省自然科學(xué)基金項(xiàng)目（2013ZRE28089）。

supported by the Natural Science Foundation of Shandong Province (2013ZRE28089).

2016-09-12收到初稿，2016-09-22收到修改稿。

聯(lián)系人及第一作者：王宇紅（1970—），男，博士，教授。