例談高中數(shù)學(xué)課堂中的“數(shù)學(xué)實驗”

連信榕

伽利略的比薩斜塔自由落體實驗，推翻了先賢亞里士多德的落體理論；牛頓的棱鏡分解太陽光實驗讓我們看到了七色的陽光；卡文迪許的扭秤實驗精確測量出了萬有引力常數(shù)……，顯然，物理學(xué)是依賴實驗的科學(xué)，居里夫人經(jīng)典的提取鐳實驗，門捷列夫的元素周期表都離不開化學(xué)實驗，孟德爾更是從豌豆實驗中發(fā)現(xiàn)了曠世的生物遺傳律。

可以說物理、化學(xué)、生物都離不開實驗，那么數(shù)學(xué)呢？數(shù)學(xué)需要實驗嗎？

答案是肯定的！數(shù)學(xué)需要實驗！著名教育家G‘波利亞指出：“數(shù)學(xué)有兩個側(cè)面，一方面它是歐幾里德式的嚴(yán)謹(jǐn)科學(xué)，從這個方面看，數(shù)學(xué)像是一門系統(tǒng)的演繹科學(xué)；但另一方面，創(chuàng)造過程中的數(shù)學(xué)，看起來卻象一門試驗性的歸納科學(xué)，”這里我們主要來談?wù)劦诙€方面，筆者認(rèn)為數(shù)學(xué)實驗是指學(xué)生在教師的引導(dǎo)下，利用各種實驗器材，包括圖形計算器，數(shù)學(xué)軟件等工具，動手實踐，自主探索，從而發(fā)現(xiàn)規(guī)律，提出猜想，并驗證猜想的過程，以下，通過幾個案例談?wù)剶?shù)學(xué)實驗的創(chuàng)設(shè)策略。

案例1直線與平面的垂直判定——有趣的折紙活動蘊含著數(shù)學(xué)定理

實驗器材：三角形紙片、矩形紙片、半圓紙片各一張。

實驗?zāi)康模和ㄟ^翻折紙片讓三種紙片立在桌面上，

問題設(shè)置：（1）這三種紙片都能通過翻折立在桌面上嗎？

（2）翻折一次能做到嗎？

（3）它們的折痕和桌面是什么關(guān)系？

（4）它們的折痕在各自紙片中有什么共同點？

（5）你能將這個實驗轉(zhuǎn)化為數(shù)學(xué)語言嗎？

評析學(xué)生通過折三種類型的紙片歸納出線面垂直的判定定理：若一條直線垂直面內(nèi)的兩交線，則線面垂直，顯然地，通過教師的有效創(chuàng)設(shè)，學(xué)生通過思考、操作、實驗、歸納、猜想、修正，感受了知識的發(fā)生發(fā)展的過程，而學(xué)生親歷數(shù)學(xué)知識的建構(gòu)過程，正體現(xiàn)了以學(xué)生為主體的課程理念，也符合學(xué)生的認(rèn)知規(guī)律，

案例2糖水變甜了嗎？——喝杯糖水讓數(shù)學(xué)課與眾不同

實驗器材：一杯開水和若干糖，

實驗?zāi)康模和ㄟ^往開水中加糖并喝糖水提取數(shù)學(xué)解釋，

問題設(shè)置：（1）往白開水中加一勺糖，味道會發(fā)生什么樣的變化？

（2）繼續(xù)往糖水中加一勺糖，味道與剛才相比發(fā)生怎樣的變化？

（3）你能用數(shù)學(xué)語言解釋這一變化嗎？

（4）你能證明這個數(shù)學(xué)規(guī)律嗎？

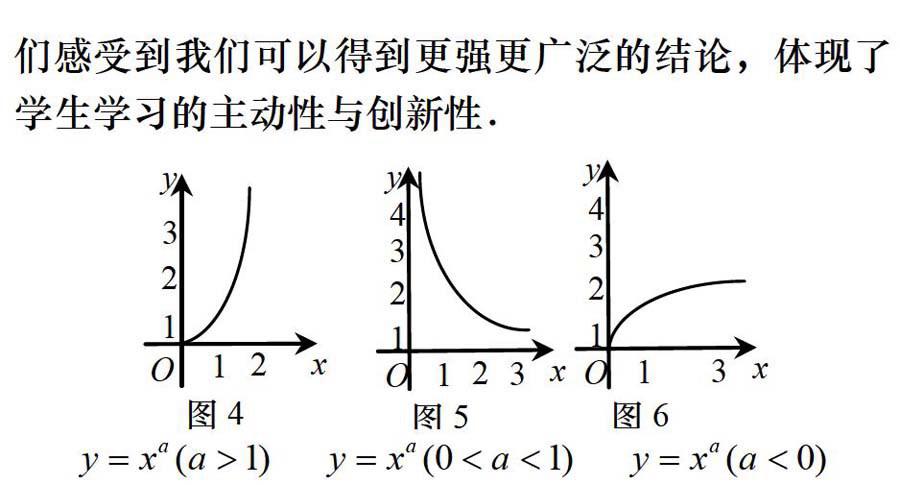
案例3冪函數(shù)圖像的畫法——數(shù)學(xué)軟件帶來的數(shù)學(xué)實驗革命

評析本案例中的函數(shù)圖像對高中學(xué)生而言，無法通過傳統(tǒng)的演繹推理得到，必須通過數(shù)學(xué)實驗完成，而《超級畫板》便為它提供了一個數(shù)學(xué)實驗室，通過操作，學(xué)生驚訝地發(fā)現(xiàn)規(guī)律（如圖4-6），再結(jié)合定義域和奇偶性即可得到任意的有理指數(shù)冪的冪函數(shù)圖像畫法，在該案例中，通過數(shù)學(xué)實驗，讓學(xué)生們感受到我們可以得到更強更廣泛的結(jié)論，體現(xiàn)了學(xué)生學(xué)習(xí)的主動性與創(chuàng)新性。

案例4班級里會出現(xiàn)兩位同學(xué)同年同月同日生嗎？一調(diào)查實驗推翻固有認(rèn)知

實驗器材：調(diào)查問卷

實驗?zāi)康模禾骄堪嗉墸?0人）中至少出現(xiàn)兩位同學(xué)同年同月同日生的概率。

問題設(shè)置：（1）如果兩個人同年同月同日生，是不是一件很神奇的事？

（2）這里的“神奇”二字，用數(shù)學(xué)解釋是什么？

（3）我們班級有50名同學(xué)，認(rèn)為會出現(xiàn)同年同月同日生的同學(xué)請舉手。

（4）請同學(xué)A公布調(diào)查年級六個班的結(jié)果（課前安排）。

（5）調(diào)查結(jié)果是否推翻了你的固有認(rèn)知呢？你能找到它的數(shù)學(xué)解釋嗎？案例5拍了幾次手？一一游戲讓數(shù)學(xué)更具親和力實驗器材：紙和筆（用于記錄）。

實驗?zāi)康模涸O(shè)計拍手游戲，通過游戲方式得到數(shù)學(xué)結(jié)論并加以證明。

問題設(shè)置：設(shè)置拍手游戲如下：5位同學(xué)（ABcDE）圍坐一圈，A報數(shù)l，B報數(shù)l，c報數(shù)2，D報數(shù)3，……，此后按順序每位同學(xué)報的數(shù)是前兩位報數(shù)的總和，當(dāng)報出的數(shù)字為3的倍數(shù)時，該同學(xué)拍手一次。

（1）統(tǒng)計拍手的情況，能發(fā)現(xiàn)規(guī)律嗎？

（2）能將上述規(guī)律提煉出數(shù)學(xué)語言并證明嗎？

（3）當(dāng)報到100個數(shù)時，A同學(xué)一共拍了幾次手？

（09年福建高考數(shù)學(xué)壓軸題）

（4）能理性證明上述問題嗎？

不可否認(rèn)，教學(xué)是一項龐大的工程，方法技巧很多，而數(shù)學(xué)實驗符合新時期教師和學(xué)生的需求，正成為教學(xué)技能中的重要一環(huán)，其實在發(fā)達(dá)國家，數(shù)學(xué)實驗早已成為常見的教學(xué)形式甚至是教學(xué)內(nèi)容，他們不僅有實驗教材，還有專屬的數(shù)學(xué)實驗室，顯然，我們在這方面還有很長的路要走，本文通過若干案例分析了操作性數(shù)學(xué)實驗，思維性數(shù)學(xué)實驗，計算機輔助性數(shù)學(xué)實驗，驗證性數(shù)學(xué)實驗等各類數(shù)學(xué)實驗的形式，不僅豐富了教師的教學(xué)形式，給相對枯燥的數(shù)學(xué)課堂帶來了活動與生機；而且發(fā)展了學(xué)生的數(shù)學(xué)素養(yǎng)，創(chuàng)造性地解決了實際問題，

數(shù)學(xué)是科學(xué)之王，科學(xué)需要實驗，數(shù)學(xué)更需要實驗！