基于時變失效率的繼電保護可靠性

李永亮,何瑞文,晏浩然

(廣東工業大學,廣州 510006)

?

基于時變失效率的繼電保護可靠性

李永亮,何瑞文,晏浩然

(廣東工業大學,廣州 510006)

為了在線評估繼電保護可靠性,提出一種基于時變失效率計算可靠性算法,根據影響繼電保護系統可靠性因素進行建模,并建立以硬件數學模型、軟件數學模型、人員失誤模型及其他影響可靠性因素為對象的狀態空間圖,求解繼電保護系統可靠性指標。最后,以一實際系統保護系統參數為例,進行了求解單套保護系統及雙重化保護系統的可靠性指標計算,結果表明該算法能更精確實時地反應保護系統的可靠性性能指標,并為保護系統的檢修決策提供參考依據。

繼電保護;可靠性評估;時變失效率;狀態空間

電力系統穩定的三道防線的第一道是繼電保護裝置有選擇性的快速、準確切除故障,而且繼電保護的四性中可靠性最為重要,因此對繼電保護可靠性的研究十分必要。

目前，評估繼電保護可靠性的方法有很多種,大多是以恒定失效率為基礎的指標計算和建模[1-4],馬爾科夫狀態空間法是其中最常用的一種,從最早的7狀態馬爾科夫模型[5],到加入人為因素的8狀態模型[6],逐漸細化模型得到計及后備保護和一、二次系統的多模型[7-9],以及到最后對馬爾科夫改進的半馬爾科夫模型[10]。然而,上述工作都是基于保護裝置恒定失效率的估算,而恒定失效率準確性較低,影響可靠性評估的精度,且隨著狀態量的增加對精度的影響越發明顯。另外,基于恒定失效率的可靠性評估得到的可用度指標只能以穩態值的形式存在,不適用于繼電保護的實時在線風險評估,且影響繼電保護裝置最佳檢修周期的準確性。而基于時變失效率[11-14]的可靠性評估能很好的反應繼保系統可靠性狀態隨時間的變化情況,為繼電保護的在線風險評估提供參考依據。所以,本文用馬爾可夫(Markov)狀態空間法定量計算了繼電保護的綜合可用度,并通過線性擬合得到的可用度函數來確定最佳檢修周期。

1 繼電保護可靠性評估

1.1 可靠性指標

繼電保護系統有3種運行狀態:正常狀態、不正常狀態及故障狀態,失效是導致故障的直接原因。失效率的定義:系統在已經正常工作了t時間情況下,在t時間之后的無窮小的時間Δt內發生故障的概率[15],其計算公式為

(1)

式中:T為繼電保護系統正常工作的時間。

可用度是指系統在規定的工況下,t時刻的正常工作概率,其計算公式為

(2)

式中:μ為修復率,λs(t)為故障率。

1.2 硬件失效模型

通過對大量同類型元件的故障數據研究表明繼電保護硬件裝置的故障率曲線呈“浴盆形狀”[15],該曲線由調試期、偶發失效期和老化期3部分組成,如圖1所示。

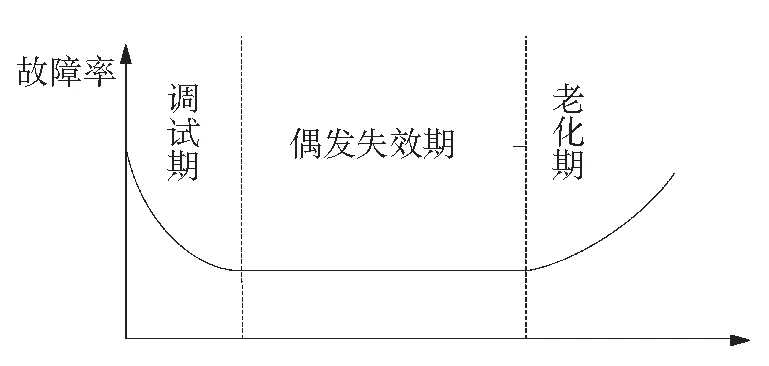
圖1 失效率隨時間變化曲線

調試期內產品由于設計、制造的缺陷以及與外界環境的磨合,因此期間故障率很高，經過一段時間的調試,元件的故障率就會降下來進入偶發失效期。偶發失效期在整個失效期內占主導地位,在偶發失效期內,其失效率函數可近視為一常數。老化期內,由于元件及絕緣層的老化,斷路器、隔離開關等設備的疲勞,接近設備的有效壽命,因此元件的失效率呈指數增長。偶發失效期和老化期的失效率函數有本質的不同,因此在擬合這兩種函數時采用不同的分布函數。

1.2.1 偶發失效估算

繼電保護裝置硬件是由各個元件經各種串并聯組合而成,偶發硬件失效是指由各元件部分或全部發生偶然故障導致整個系統失效的情況(如信號采樣值傳輸的延時、誤碼及丟包導致誤動拒動,不同的運行方式同一個整定值,復用通道受干擾、裝置瞬間缺陷或外界環境引起等)。偶發失效率可近似為一常數,一般采用指數分布函數進行擬合。指數分布函數的概率密度函數和累積分布函數為:

(3)

(4)

用最小二乘擬合方法得到的指數分布函數偶發失效率為

(5)

式中:n為偶發裝置硬件失效總數;∑t1為偶發裝置運行總時間;∑t2為正常運行繼電保護裝置總運行時間。

1.2.2 老化期的失效估算

老化期的失效誘因是裝置的老化、絕緣材料絕緣性能的降低等等。對于繼電保護裝置的老化失效率,目前大多使用二參數的Weibull分布函數進行擬合,其分布函數及失效函數為:

(6)

(7)

式中:m和k分別為函數的形狀和尺度參數。

進一步得到失效率函數為

(8)

式中:R(t)為可靠度函數,R(t)=1-F(t)。

1.2.3 硬件失效總失效率

一般廠家在保護裝置出廠前都經過嚴格、充分的測試,故本文不再考慮繼電保護裝置處于調試期的情況。

在不考慮設備調試期的情況下,得到硬件失效的總失效率為偶發失效率和老化失效率的線性相加,其計算公式為

λ(t)=λ0+λ1(t)

(9)

1.3 軟件失效模型

軟件失效一般指軟件算法的失效,軟件失效和硬件失效都是隨機過程,但軟件失效與硬件失效有些不同,軟件系統不存在老化過程,在調試期結束后投入使用期間,存在的錯誤會很少,且一經修復就不會再發生同樣的錯誤,因此其失效率還會不斷下降,但其變化的幅度不大可以近似為一定值。IEEE把軟件失效定義為在規定的時間、規定的條件軟件發生的故障概率。從20世紀1971年J-M模型的發表到今天至少有幾百種可靠性的模型,比較實用的有G-O模型、Musa模型、Logarithmic exponential模型及John Musa模型。本文采用Logarithmic exponential模型[16],該模型的失效率為

λs=λ1e-θυ

(10)

式中:λ1為初始失效率;θ為失效減少系數;υ為系統運行中累積發現的錯誤。

1.4 人員誤動模型

縱然隨著智能電網的大力發展,電力系統的智能化程度越來越高,無人值守的變電站也越來越多,但只要有人的存在就避免不了人為因素的失效,且隨著裝置硬件和裝置軟件的可靠性不斷提高,人員可靠性的研究就顯得越來越重要。人員可靠性的研究有諸多困難,用于研究人員失效的數據太少,并且具有不確定性。目前人員可靠性分析有兩種:一是對歷史數據的分析得到人員可靠性的模型,二是基于多因素的層次分析人為誤操作率。本文采用第一種,采用通用數據(來自相關行業的人員失誤數據集專家判斷)進行分析,應認知可靠性模型(HCR)三參數的韋布爾分布(Weibull)擬合進行計算[17],其失效率公式為

(11)

式中:t為允許操作人進行響應的時間;T0.5為操作人員的執行時間;α、β、γ為與行為相關的參數。

1.5 其他失效模型

除了上述失效因素,繼電保護的隱形(隱藏)故障也受到廣泛關注。隱形故障對電網的安全運行威脅很大且很難被發現,當系統運行狀態發生變化,如出現擾動、發生故障或因保護系統切除線路而造成潮流重新分配時就被觸發而導致連鎖故障的發生。 隱形故障被定義為“一種保護系統中的永久缺陷,此缺陷將導致繼電保護系統不正確或不適當的切除電路元件,其后果是造成其他的錯誤切除事件[18]”。

目前確定繼電保護隱形故障的具體概率主要有2種途徑:概率統計分析法和現有概率模型法。本文選用概率模型法即保護裝置隱形故障誤切線路的概率模型[19],得到隱形故障的故障率為

(12)

式中:m為保護裝置的數量;j為保護裝置;P(Kj)為保護裝置j的風險區域故障概率;P(fj)為保護裝置j隱形故障發生的概率。

2 狀態空間法求解繼電保護可靠性指標

數字繼保裝置的工作過程可以看成一馬爾科夫隨機過程,因此本文采用狀態空間法來求解其可靠性指標。

在建立系統狀態空間圖時做了一些假設:1)系統運行狀態只考慮正常狀態和工作狀態,不正常運行狀態不考慮。2)假設各個狀態都是獨立的,在任何情況下都只發生一種故障,不會出現2種或2種以上故障狀態。3)本文不考慮檢修狀態,目前檢修都是運行檢修,對系統影響不大。4)可修復的故障在修復后及可立即使用,不引入新的故障。5)不考慮故障的類型(即故障不分拒動和誤動)。6)認為修復率是一個恒定值。

2.1 單套保護系統的綜合可靠性

在以上的假設下得到數字繼保裝置的狀態空間如圖2所示。

狀態0—正常狀態;狀態1—硬件故障導致的狀態;狀態2—軟件故障導致的失效狀態;狀態3—人為導致的失效狀態;狀態4—其他因素導致的失效狀態;λ1(t)—繼電保護系統硬件失效的失效率;μ1—修復率;λ2(t)—軟件失效的失效率;μ2—修復率;λ3(t)—人員失誤的失效率;μ3—修復率;λ4(t)—隱形故障導致的失效率;μ4—修復率。

圖2 單套繼電保護系統狀態空間圖

Fig.2 State space diagram of single set relay protection system

由狀態空間圖2得到系統的狀態轉移密度矩陣A及各狀態的駐留矩陣P為:

(13)

P=[p0,p1,p2,p3,p4]

(14)

PA=0

(15)

(16)

將式(13)(14)帶入式(15)結合式(16)解得:

p0=μ1μ2μ3μ4/(μ1μ2μ3μ4+λ1μ2μ3μ4+μ1λ2μ3μ4+μ1μ2λ3μ4+μ1μ2μ3λ4)

(17)

(18)

正常狀態0的狀態駐留概率p0即為系統的保護綜合可用度。

2.2 雙重化保護系統的綜合可靠性

現假定保護系統采用雙重化配置,且各主保護的各項可靠性指標都一樣,其狀態轉移關系為:狀態1表示兩套保護都正常,狀態2表示保護1故障保護2正常工作,狀態3表示保護2正常工作保護1故障,狀態4表示2套保護都故障,這4種狀態之間的轉換關系(狀態1到狀態4的過渡或狀態2到狀態3的過渡不考慮)如圖3所示。

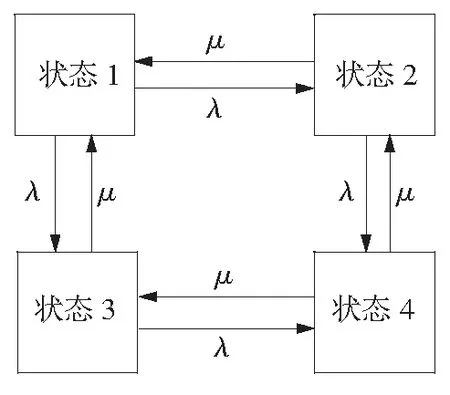
圖3 雙重化繼電保護系統的狀態空間圖

系統的一步轉移矩陣A1及駐留矩陣P1為

P1=[p0,p1,p2,p3]

(19)

(20)

由馬爾科夫理論有P1=[p0,p1,p2,p3]

(21)

(22)

由式(19)(20)(21)(22)得

(23)

系統的綜合可用度為p0。

3 算 例

3.1 數據分析

受數據來源的限制,本文選取某220 kV線路繼電保護系統,收集某地區電網的可靠性數據,并參考文獻[6、14、19、20]的部分可靠性數據。

1) 硬件失效率數據是通過對歷史數據的分析得到的指標如表1所示。

表1 硬件失效參數表格

2) 軟件可靠性參數如表2所示。

表2 軟件失效參數表格

3) 人員可靠性數據選取比較復雜,依據專家判斷選取人員行為類型參數,如表3所示,本文人員可靠性數據采用熟練型,t/T0.5=4.32。

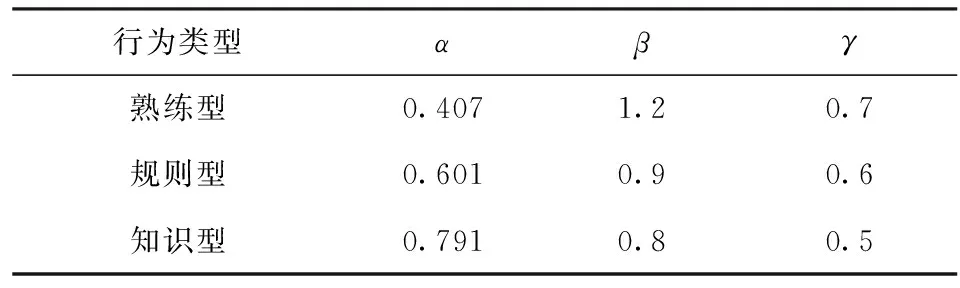
表3 人員行為類型參數選取表

4) 引發隱形故障的因素很多,本文只考慮惡劣環境因素引發的隱形故障。

λy=5.7974×10-6·h-1

5) 根據實際運行的經驗并結合歷史統計數據,得到各種故障的修復率如表4所示。

表4 各種故障的修復率

由表1、2、3及式(5)、(8)、(9)、(10)、(12)得該系統的可靠性指標如表5所示。

表5 各種故障的失效率

3.2 單套、雙重化保護系統可靠性及其對比

3.2.1 單套保護可靠性

因狀態空間法只能求取恒定失效率情況下的可靠性指標,故現將保護裝置的硬件失效率按時間形成離散時間點,結合表4和表5帶入式(17),得到的綜合可用度隨時間變化動態如圖4所示。

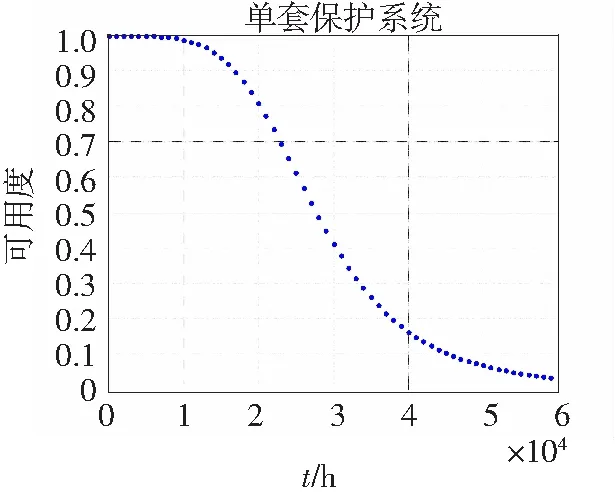
圖4 單套保護系統的綜合可用度值

現將得到的可靠度離散點通過MATLAB擬合工具箱線性回歸擬合得到函數為

(24)

擬合的得到的曲線如圖5所示。

圖5 單套保護系統的擬合函數圖

為了評價擬合函數的誤差,現引入可決系數R2來評定擬合優度。

(25)

經計算得到該函數的可決系數R2=0.9999,可以看出此函數能很好的擬合單套保護系統可靠度隨時間變化的趨勢。

在確定最佳檢修周期時,可以假設當系統的綜合可用度小于0.99時需要停運檢修。令

f(t)≤0.99

(26)

則得：當時間t=9500 h時就需要檢修。

3.2.2 雙重化保護可靠性計算

單套保護系統的綜合失效率可以看成系統從正常狀態轉移到所有故障狀態的失效率之和。因此單套保護系統的綜合失效率為

λ=λ1+λ2+λ3+λ4

(27)

單套繼電保護系統總的故障修復率為

(28)

將式(27) (28)帶入式(23)得到雙重化保護綜合可用度,如圖6所示。

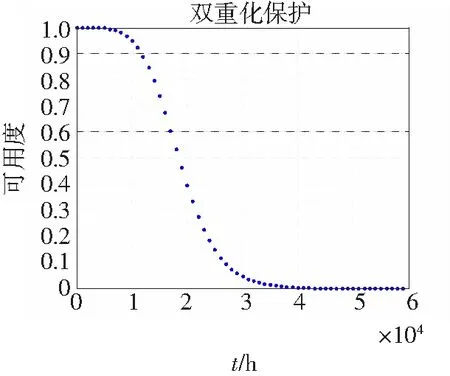
圖6 雙重化保護系統的綜合可用度值

通過線性擬合得到的可用度函數為

(29)

擬合的得到的曲線如圖7所示。

圖7 雙重化保護系統的擬合函數圖

經計算得到該函數擬合優度R2=0.9998。

假設當系統綜合可用度低于0.99時需要檢修,帶入式(29)可得:當t=6820 h就需要停運檢修。

兩種保護配置數據的交叉比較如圖8示。

圖8 不同保護配置方案的比較

從圖8可以看出,雙重化保護在前4517 h的總可用度比單套保護的高,但由于系統的復雜化導致在4517 h之后雙重化保護系統的可靠性會低于單套保護系統,且其投資成本會成倍增加。在同等條件下雙重化保護的檢修周期要比單套保護的檢修周期要短。一般情況,認為220 kV及以上電壓等級系統都要采用雙重化配置,由此可以看出較重要系統為了滿足其高可靠性的條件下會犧牲一部分經濟性。

4 結 論

本文在前人可靠性研究的基礎上針對恒定失效率不能滿足繼電保護系統實時運行的風險評估問題,提出了基于時變失效率的可靠性評估方法。在硬件模型搭建方面做了一些改進,相比其他文章硬件的恒定失效上加入老化失效,能更真實的反映硬件失效特性。

2012年和2013年全國220 kV及以上電壓等級交流系統繼電保護正確動作率分別為99.89%和99.92%[20],而本文在考慮如今電力電子設備的可靠性大幅提高及人員技術的成熟度越來越高等因素上,算出的兩套系統在投入運行的前期的綜合可用度分別為99.84%與99.97%,對比數據可知,該算法得到的結果符合實際情況。

[1] 張沛超, 高翔.全數字化保護系統的可靠性及元件重要度分析[J].中國電機工程學報,2008,1(28):77-82.ZHANG Peichao,GAO Xiang.Analysis of reliability and component importance for all-digital protective systems [J].Proceeding of the CSEE,2008,1(28):77-82.

[2] JIANG Kai,SINGH C.Reliability modeling of all-digital protection system including impact of repair [J].IEEE Trans on Power Delivery,2010,25(2):579-587.

[3] DAI Zhihui,WANG Zengping.Protection dynamic reliability analysis system based on 3RF technique[J].IEEE Trans on Power System,2011,26(3):1137-1144.

[4] SCHWEITZER E O,ANDERSON P M,et al..Reliability analysis of transmission protection using fault tree method[C]//Protection of the 24thAnnual Western Protective Relay Conference,October 21-23,1997,Spokance WA,USA:1-17.

[5] 王鋼,丁茂生,李曉華,等.數字繼電保護裝置可靠性研究[J].中國電機工程學報, 2004,24(7):48-53.WANG Gang,DING Maosheng,LI Xiaohua,et al.Reliability analysis of digital protection[J].Proceeding of the CSEE,2004,24(7):48-53.

[6] 陳少華,馬碧燕,雷宇,等.綜合定量計算繼電保護系統可靠性[J].電力系統自動化,2007,31 (15):111-115.CHEN Shaohua,MA Biyan,LEI Yu,et al.Integrative and quantitative calculation of reliability for relay protection system[J].Automation of Electric Power Systems,2007,31(15)::111-115.

[7] 王樹春.雙重化繼電保護系統可靠性分析的數學模型[J].繼電器,2005,23(18):6-10.WANG Shuchun.Markov model for reliability analysis of dual-redundant relays[J].Relay,2005,23(18):6-10.

[8] 熊小伏,陳飛,周家啟,等.計及不同保護配置方案的繼電保護系統可靠性[J].電力系統自動化,,2008,32(7):21-24.XIONG Xiaofu,CHEN Fei,ZHOU Jiaqi,et al.Reliability of protection relay systems with different configurations[J].Automation of Electric Power Systems,2008,32(7):21-24.

[9] 付聰,安靈旭,方華亮,等.繼電保護系統對一次設備可靠性的影響研究[J].電力系統保護與控制,2013,41(11):38-44.FU Cong,AN Lingxu,FANG Huangliang,et al.Study on the influence of protection system on reliability of primary equipment[J].Power System Protection and Control,2013,41(11):38-44.

[10] 汪隆君,王鋼,李博,等.基于半馬爾可夫過程的繼電保護可靠性建模[J].電力系統自動化,2010,34(18):6-10.WANG Longjun,WANG Gang,LI Bo,et al.Reliability modeling of a protection system based on semi Markov process[J].Automation of Electric Power Systems,2010,34(18):6-10.

[11] FARAG A S,WANG C.Failure analysis of composite dielectric of power capacitors in distribution system[J].IEEE Trans on Dielectrics and Electrical Insulation,1998,5(4):583-585.

[12] MOON J F,KIM J C,LEE H T.Time-varying failure rate extraction in electric power distribution equipment[C]//Proceedings of the 19th International Conference on Probabilistic Methods Applied to Power Systems, June 11-15,2006, Stockholm,Sweden.

[13] CHU C M,MOON J F,LEE H T,et al.Extraction of time-varying failure rates on electric power distribution equipment considering failure modes and regional effects[J].International Journal of Electrical Power &Energy systems,2010,32(6):721-727.

[14] 王睿琛,薛安成,畢天姝,等.繼電保護裝置時變失效率估算及其區域性差異分析[J].電力系統自動化,2012,36(5):11-15.WANG Ruichen,XUE Ancheng,BI Tianshu,et al.Time-varying failure rate estimation of relay protection devices and their regional differences analysis[J].Automation of Electric Power Systems,2012,36(5):11-15.

[15] 郭永基.可靠性工程原理[M].北京:清華大學出版社,2002.GUO Yongji.Principle of reliability engineering[M].Beijing:Tsinghu University Press, 2002.

[16] BOWLES JB.A combined hardware,software and usage model of network reliability and availability,1990.Proceedings of Ninth Annual International Phoenix Conference on Computers and Communications.21-23 March 1990 Pages:649-654.

[17] 張力,黃曙東,何愛武,等.人因可靠性分析方法[J].中國安全科學學報,2001, 11(3):6-16.ZHANG Li,HUANG Shudong,HE Aiwu,et al.Methods for human reliability analysis[J].China safety science journal,2001,11(3):6-16.

[18] TAMRONGLAK S.Analysis of power system disturbances due to relay hidden failures[D].Blacksburg,VA,USA:Virginia polytechnic and State University,1994.

[19] 熊小伏,蔡偉賢,周家啟,等.繼電保護隱藏故障造成輸電線路連鎖跳閘的概率模型[J].電力系統自動化,2008,32(14):6-10.XIONG Xiao fu,CAI Wei xian,ZHOU Jia qi,et al.Probabilistic model for transmission lines cascading trips caused by hidden failure in relay protection[J].Automation of Electric Power Systems,2008,32(14):6-10.

[20] 張烈,呂鵬飛,申華,等.2013年國家電網公司220 kV及以上電壓等級交流系統繼電保護設備及其運行情況分析[J].電網技術,2015,39(4):1153-1159.ZHANG Lie,LV Pengfei,SHEN Hua,et al.Analysis on protective relaying and its operation conditions of SGCC in 220 kV and above voltage AC systems in 2013[J].Power System Technology,2015,39(4):1153-1159.

(責任編輯 郭金光)

Reliabilityan alysis of relay protection based on time-varying failure rate

LI Yongliang, HE Ruiwen, Yan Haoran

(Guangdong University of Technology, Guangzhou 510006, China)

This paper proposed a new reliability algorithm based on time-varying failure for online evaluation on the reliability of relay protection.According to the factorsinfluencing the reliability of the relay protection system, this paper established the model,withthe state space diagram based on the mathematical model of hardware andsoftware,human error models and other factors influencing the reliability, and solved the reliability index of the relayprotection system.Finally, takingpractical system parameters astheexample, it calculated the reliability index of the single-setand the dual protection systems.The results demonstrate that the proposed algorithm can more accuratelyreflect the reliability performanceindex of protection system in real time, providing the

for the maintenance decision of protection system.

relay protection;reliability evaluation;time-varying failure rate;state space

2016-07-18。

國家自然科學基金(基金編號51377026)。

李永亮(1990—),男,碩士研究生,主要研究方向為繼電保護可靠性。

TM77

A

2095-6843(2016)05-0405-07