電勵磁爪極發(fā)電機氣隙磁場解析模型

左曙光, 吳雙龍, 吳旭東, 林 福, 鄧文哲

(同濟大學 新能源汽車工程中心,上海 201804)

?

電勵磁爪極發(fā)電機氣隙磁場解析模型

左曙光, 吳雙龍, 吳旭東, 林 福, 鄧文哲

(同濟大學 新能源汽車工程中心,上海 201804)

為了對電勵磁爪極發(fā)電機的性能進行快速計算和分析,提出一種新的氣隙磁場解析計算模型.利用傅里葉級數(shù)分解推導空載氣隙磁動勢、電樞反應磁動勢和氣隙磁導,基于磁勢和磁導得到空載氣隙磁場和電樞反應磁場,同時引入修正系數(shù)考慮轉子極爪形狀和定子開槽的影響.通過有限元方法和試驗結果驗證了該解析模型的準確性.該模型建立了爪極電機的氣隙磁場與電機參數(shù)之間的關系,適合在爪極發(fā)電機的初始設計階段對其氣隙磁場進行快速計算和性能優(yōu)化.

爪極發(fā)電機；磁動勢；磁導；氣隙磁場；解析模型

爪極發(fā)電機不但具有制造工藝簡單和成本低的特點,而且特殊的爪極轉子結構使其具有較高的功率密度,從而在汽車發(fā)電機領域得到了廣泛的應用[1-2].然而電勵磁爪極發(fā)電機也存在一些顯著的缺點：效率低、輸出特性差、噪聲大[3-4].尤其是作為汽車發(fā)電機使用時,一方面由于汽車發(fā)動機等傳統(tǒng)主要噪聲源的噪聲已經(jīng)得到了有效的控制,發(fā)電機已成為汽車主要噪聲源之一；另一方面汽車電子設備的大量應用,對發(fā)電機的發(fā)電性能提出了更高的要求.無論是噪聲的控制還是發(fā)電性能的提高,都與氣隙磁場密切相關,因此有必要對爪極發(fā)電機的氣隙磁場展開研究.

與普通電機不同,爪極電機的結構和磁路分布具有典型的三維性,這就給電機的設計和分析帶來了一定的困難.目前對爪極電機的研究主要采用三維有限元法和等效磁網(wǎng)絡法[5].Guo等[6-9]采用三維有限元法對爪極電機的參數(shù)和性能進行分析,雖然有限元法能對爪極電機進行精確建模,但該方法計算耗時長且不利于對電機參數(shù)進行分析,尤其是在電機設計的初始階段.相比之下,等效磁網(wǎng)絡法能夠對爪極電機的性能等進行快速計算.Ibala等[10-11]采用等效磁網(wǎng)絡法對爪極電機空載和負載下的特性進行分析,同時還考慮了飽和效應的影響.喬東偉等[12]采用等效磁網(wǎng)絡法計算了混合勵磁無刷爪極發(fā)電機的發(fā)電性能.張鳳閣等[13]建立了外永磁轉子爪極電機的等效磁路模型并進行了參數(shù)計算.Shen等[14]采用集總參數(shù)磁網(wǎng)絡模型對爪極電機進行了設計.Ibala等[15]對4種不同結構形式的爪極電機的等效磁網(wǎng)絡模型進行對比和分析.Elloumi等[16]建立了爪極電機的動態(tài)磁網(wǎng)絡模型,該模型可以考慮轉子位置的變化.Lee等[17]采用改進的磁網(wǎng)絡模型對爪極電機的特性進行分析.王群京等[18]采用三維等效磁網(wǎng)絡模型計算了混合勵磁爪極發(fā)電機的負載特性.綜合上述文獻可知,雖然等效磁網(wǎng)絡模型能夠快速計算爪極電機的性能并保證一定的精度,但由于爪極電機的結構和磁路呈三維分布,其等效磁路模型比較復雜,模型中各部分參數(shù)不易獲取,而且無法分析氣隙磁場的分布情況.

以上2種方法均不能得到氣隙磁場和電機結構參數(shù)之間的關系,不利于對爪極電機的性能進行優(yōu)化,因此有必要建立爪極電機氣隙磁場的解析計算模型.本文首先推導轉子勵磁磁動勢、電樞反應磁動勢和氣隙磁導，基于氣隙合成磁動勢和磁導得到氣隙磁場，并對氣隙磁場的頻率特性和空間階次進行分析，最后通過有限元仿真和反電動勢試驗驗證該解析模型的準確性.

1 電勵磁爪極發(fā)電機的結構和磁路

電勵磁爪極發(fā)電機的具體結構如圖1所示,包括定子鐵芯、電樞繞組、爪極轉子、勵磁繞組和轉軸等部分,其中電樞繞組繞制在定子槽中,勵磁繞組則通過支架等繞制在轉子磁軛上.當發(fā)電機工作時,勵磁繞組中通直流電產(chǎn)生軸向勵磁磁場,該軸向磁場通過轉子極爪的作用轉換成徑向磁場,具體的磁通路徑[19]如圖2所示.主磁通經(jīng)轉子爪極N極、氣隙、定子齒到達定子軛,然后經(jīng)定子齒、氣隙到達爪極S極,最后經(jīng)過轉子磁軛再回到爪極N極,從而形成一個閉合回路.

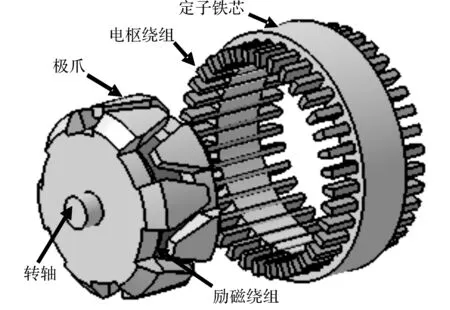
圖1 電勵磁爪極發(fā)電機結構圖Fig.1 Exploded view of electric excitation claw pole alternator

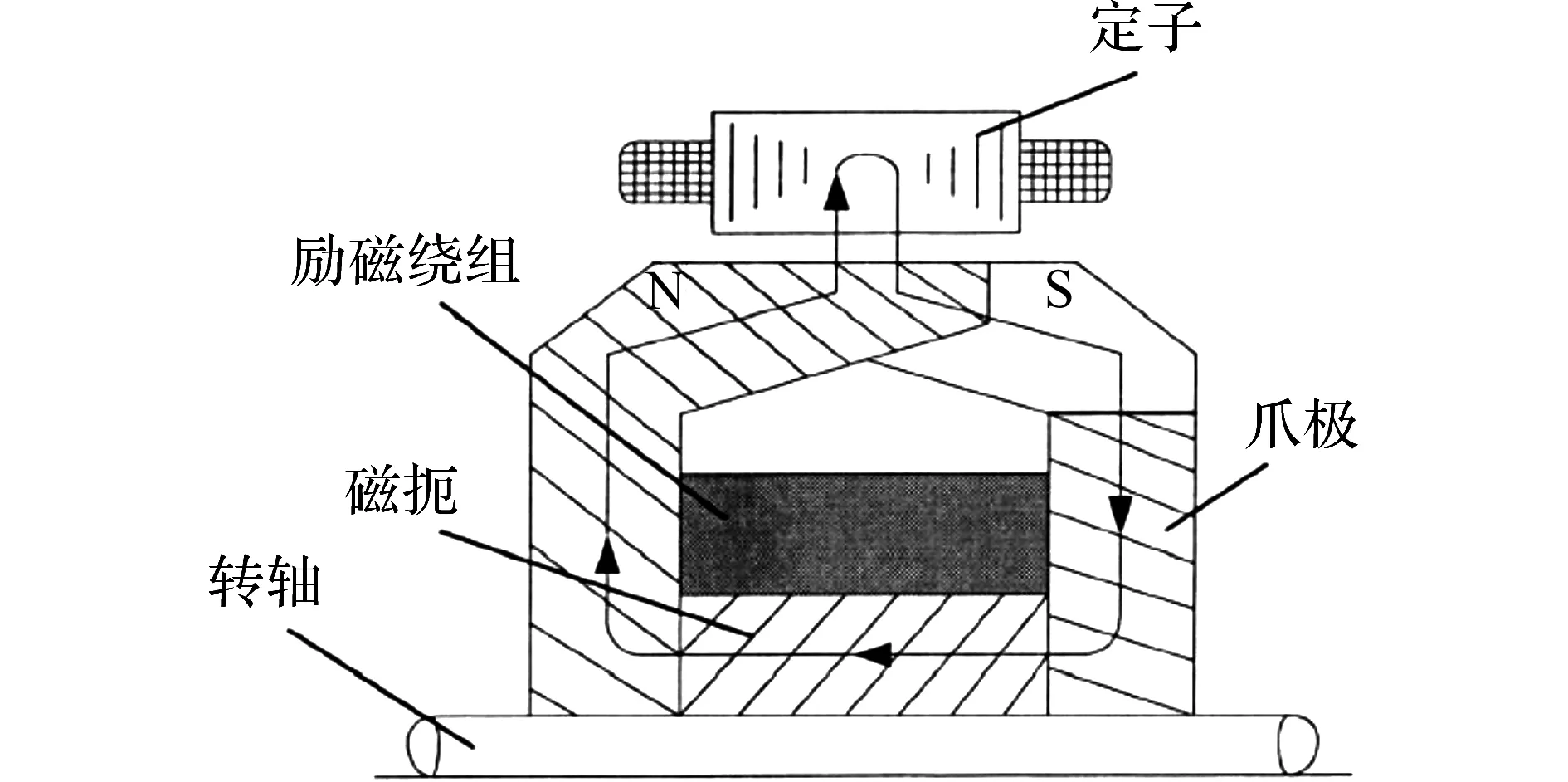
圖2 電勵磁爪極發(fā)電機主磁通磁路Fig.2 Magnetic path of main flux in electric excitation claw pole alternator

2 氣隙磁場解析推導

2.1 轉子勵磁磁動勢

根據(jù)爪極轉子的結構,將其沿周向展開,取一對極,得到如圖3所示的展開圖.假設轉子極爪長度為L,極爪兩端的寬度分別為b1和b2,在任意軸向位置z處,N極和S極的寬度分別為bN和bS.

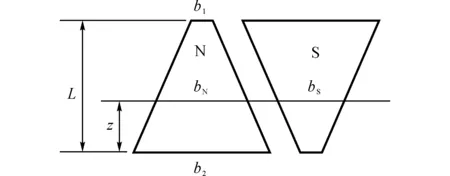
圖3 爪極轉子展開圖Fig.3 Expansion plan of claw pole rotor

由幾何關系得

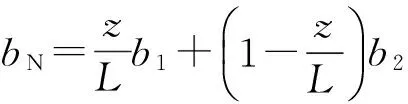
(1)

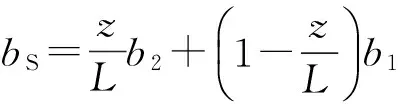
(2)

爪極電機的極距為

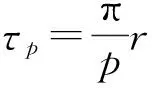
(3)

式中：r為轉子外徑；p為電機極對數(shù).任意軸向位置z處N極和S極的極弧系數(shù)分別為

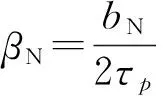
(4)

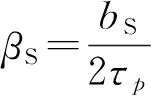
(5)

假設爪極電機定轉子鐵芯的磁導率為無窮大并且忽略漏磁的影響,根據(jù)爪極轉子的特點,勵磁繞組產(chǎn)生的勵磁磁動勢將全部通過每一對極爪[20],從而可以得到任意軸向位置處的轉子勵磁磁動勢在氣隙中的空間分布情況,具體如圖4所示.其中，F(xiàn)f為轉子上的勵磁繞組產(chǎn)生的磁動勢.

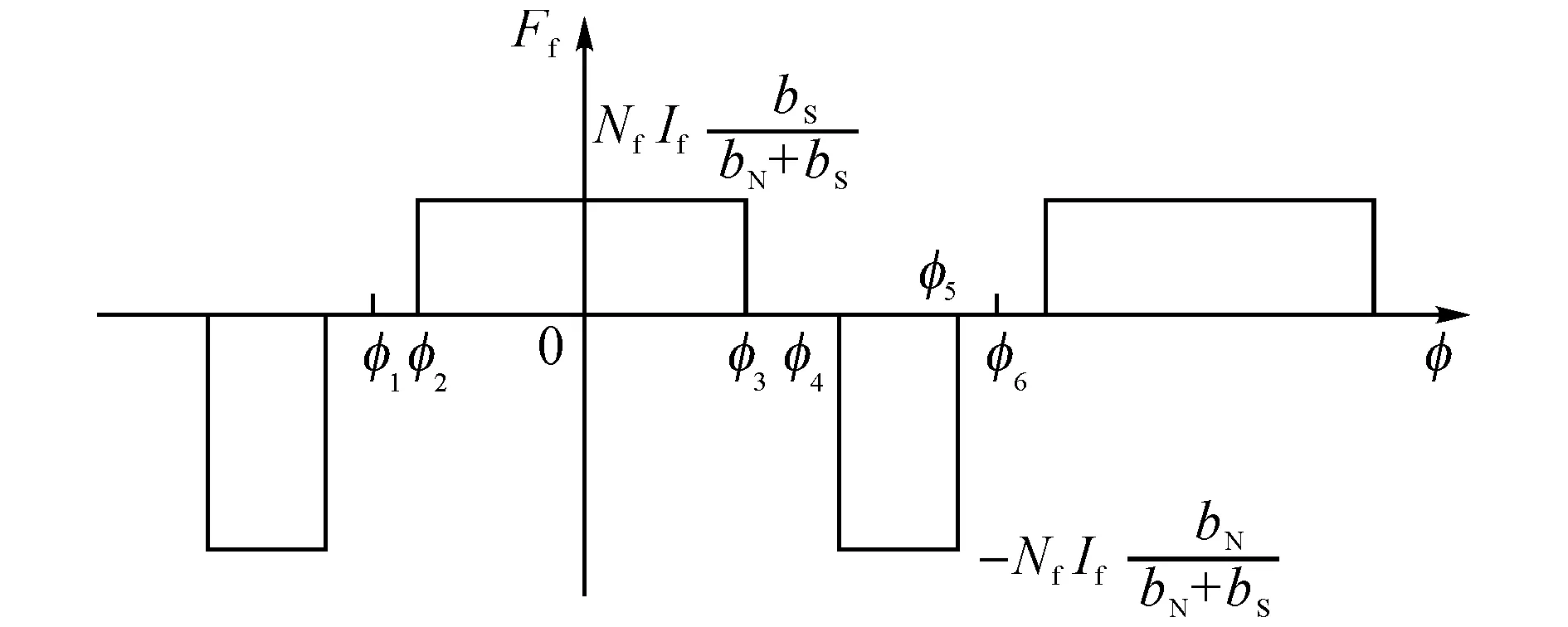
圖4 轉子繞組磁動勢Fig.4 Magnetomotive force of rotor coil

由幾何關系得

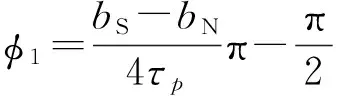
(6)

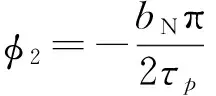
(7)

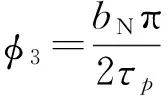
(8)

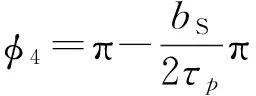
(9)

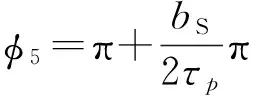
(10)

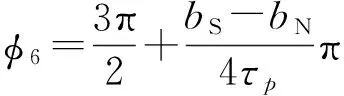
(11)

對轉子勵磁磁動勢圓周空間分布進行傅里葉級數(shù)分解,僅含余弦項：

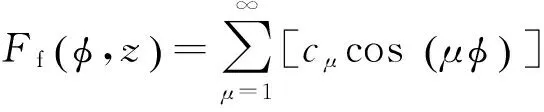
(12)

其中：

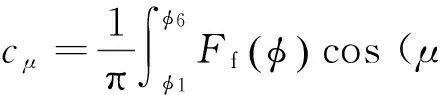
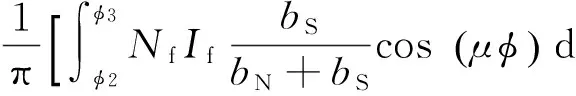
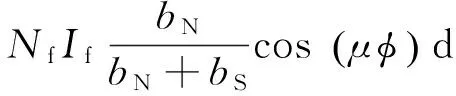
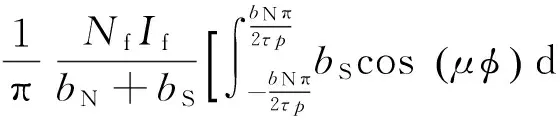
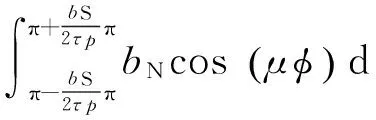
(13)

式中:φ為電角度,Nf為轉子勵磁繞組匝數(shù),If為勵磁電流.

又φ=pθ-ωet,則t時刻任意軸向位置z處的勵磁磁動勢為

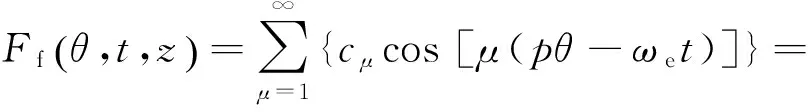
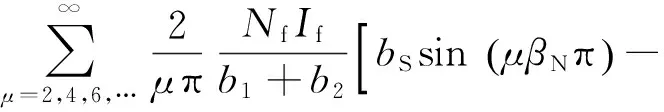
(14)

其中,

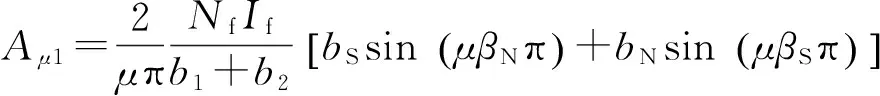
(15)

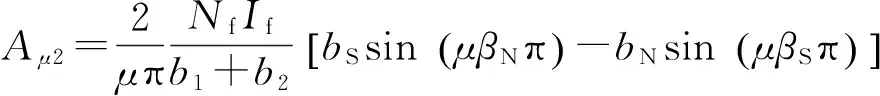
(16)

式中：θ為電機周向位置,ωe為電角速度.

由式(14)可知,爪極電機轉子磁動勢是關于時間t、電機周向位置θ和軸向位置z3個變量的函數(shù).

2.2 電樞反應磁動勢

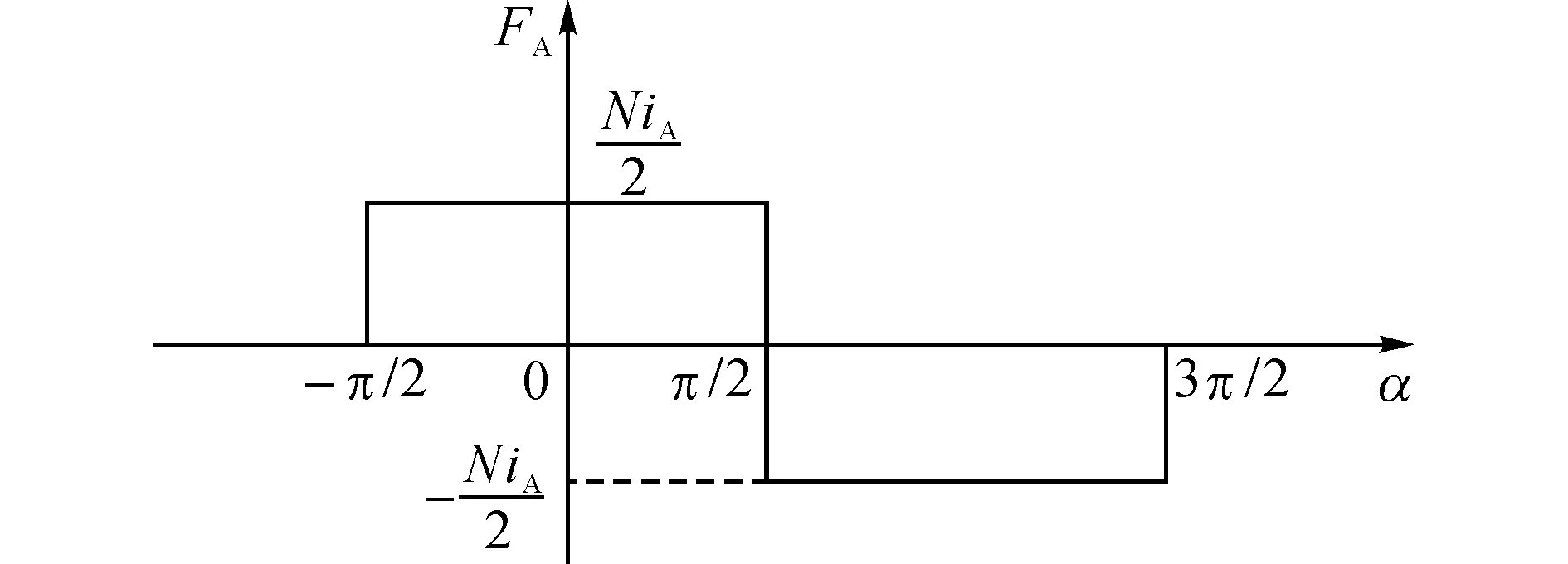
圖5 A相定子繞組磁動勢Fig.5 Magnetomotive force of stator coil of phase A

爪極發(fā)電機一般采用三相整數(shù)槽集中整距繞組,其A相繞組磁動勢的空間分布如圖5所示.對A相繞組磁動勢的空間分布進行傅里葉級數(shù)分解,僅含余弦項：

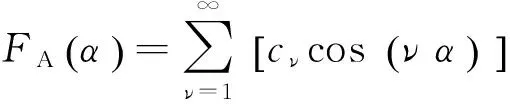
(17)

式中：

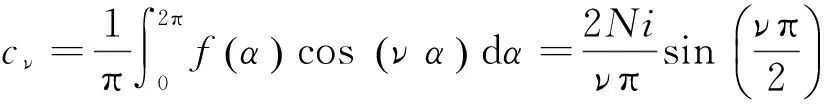
(18)

又α=pθ,故A相繞組磁動勢為

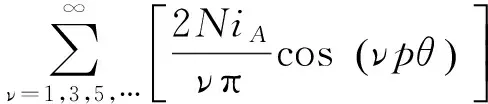
(19)

式中:α為電角度,N為定子每槽繞組匝數(shù).

忽略定子繞組電流諧波的影響,假設其三相電流為正弦波電流,即：

(20)

式中:Im為相電流幅值,φ為電流初始相位角.

ABC三相磁動勢分別為

(21)

定子繞組三相合成磁動勢為

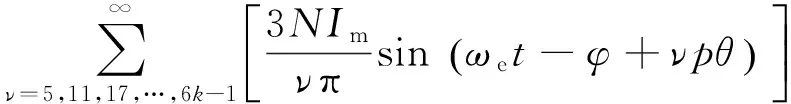
(22)

由式(22)可知,爪極電機定子繞組磁動勢是關于時間t和電機周向位置θ兩個變量的函數(shù),與軸向位置z無關.

2.3 氣隙磁導

爪極電機的轉子由N極極爪和S極極爪相互交錯排列組成,由于相鄰兩極之間存在氣隙,不能像普通徑向電機那樣把轉子看成是一個光滑的圓柱體.此外定子上還有開槽,因此氣隙磁導的計算必須同時考慮爪極轉子結構和定子開槽的影響.

2.3.1 假設定子不開槽,單獨由爪極轉子引起的氣隙磁導 假設轉子極爪間的氣隙足夠大,即該處的磁導為0,則0時刻氣隙中任意軸向位置z處的磁導分布如圖6所示.

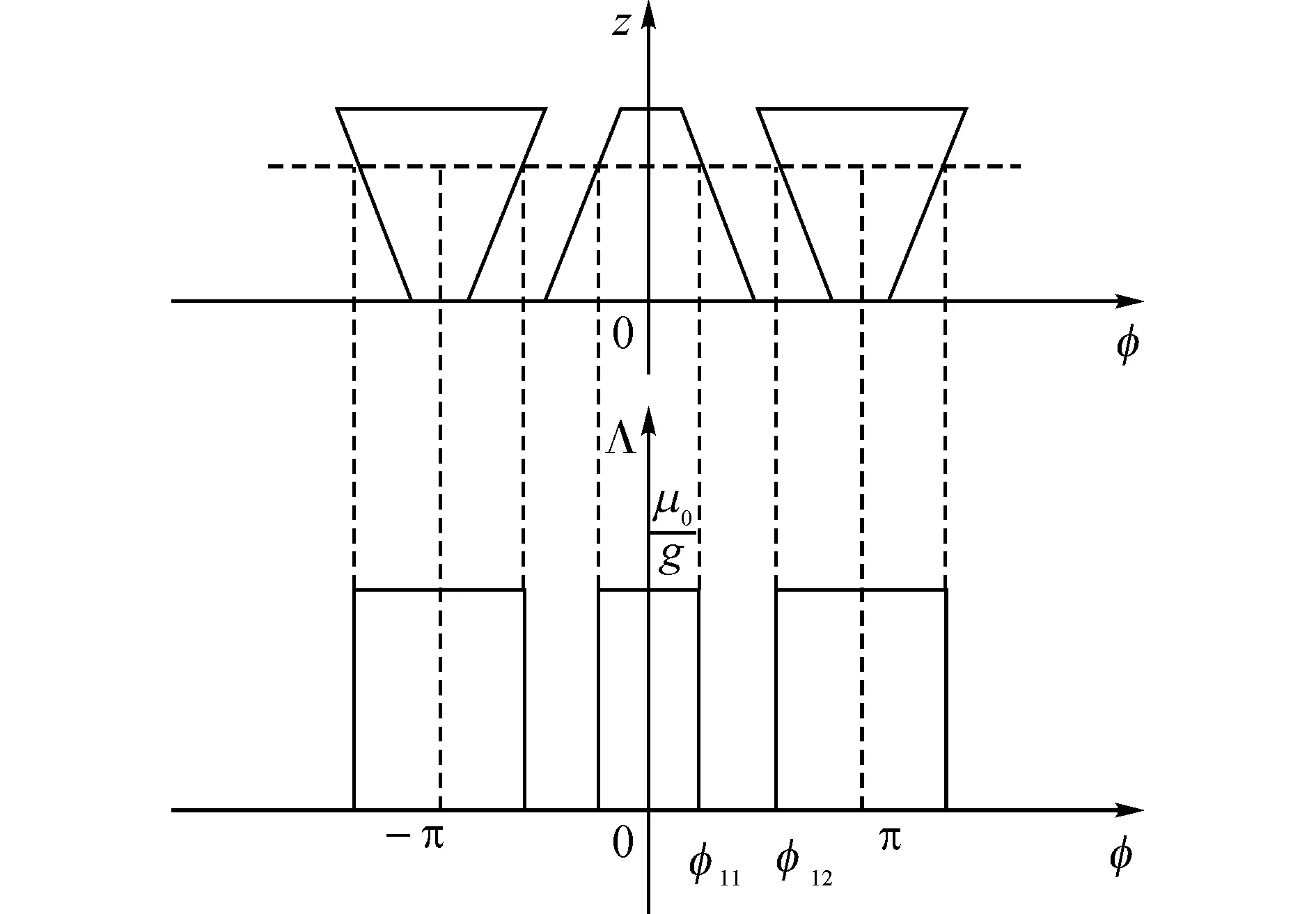
圖6 任意軸向位置處的氣隙磁導空間分布Fig.6 Spatial distribution of air gap permeance

由幾何關系得

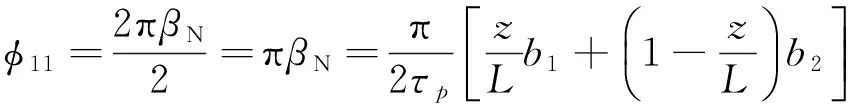
(23)

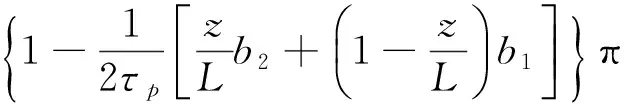
(24)

對氣隙磁導的圓周空間分布進行傅里葉級數(shù)分解：

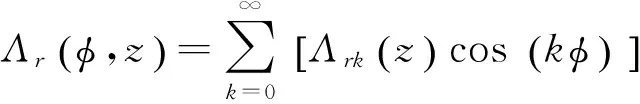
(25)

式中：

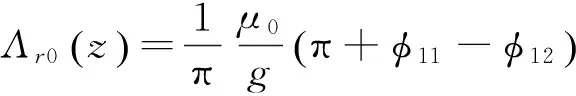
(26)

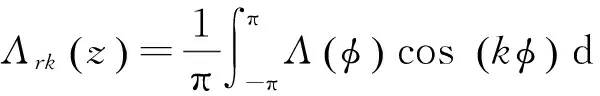
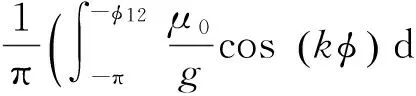
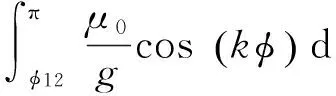
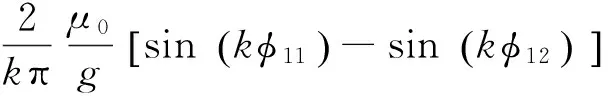
(27)

又φ=pθ-ωet,則t時刻任意軸向位置z處的氣隙磁導為

(28)

2.3.2 考慮定子開槽的影響,引入修正系數(shù) 修正系數(shù)在定子齒所對應的位置上定義為1,在定子槽口對應的位置上定義為λ,λ為定子槽口中心處的磁密與定子齒中心處的磁密的比值[21],修正系數(shù)的波形如圖7所示.

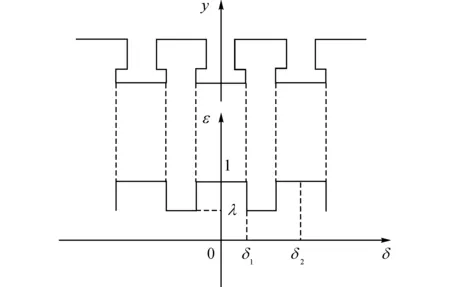
圖7 由定子開槽引起的修正系數(shù)Fig.7 Correction factor for permaeance due to stator slots

由幾何關系得

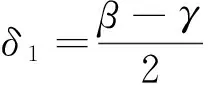
(29)

δ2=β.

(30)

式中:β=2π/S, 為槽距角；γ=b0/r,為槽口寬度角；S為定子槽數(shù)；b0為槽口寬度；r為轉子外徑.

由圖7可知,氣隙磁導修正系數(shù)是以δ2為周期的偶函數(shù),對其進行傅里葉級數(shù)分解得

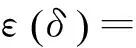
(31)

式中：

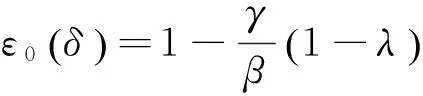
(32)

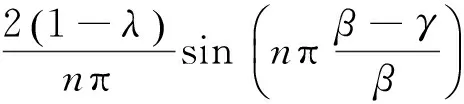
(33)

又δ=θ,則任意軸向位置z處的氣隙磁導修正系數(shù)為

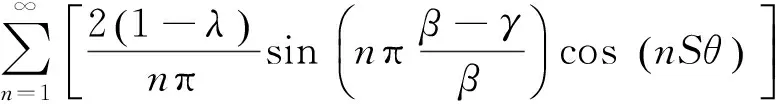
(34)

2.3.3 綜合考慮爪極轉子和定子開槽的氣隙磁導 綜合式(28)和(34)可得

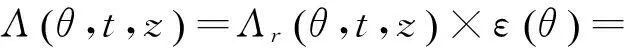
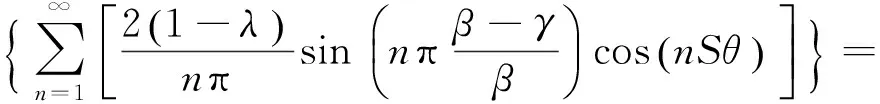
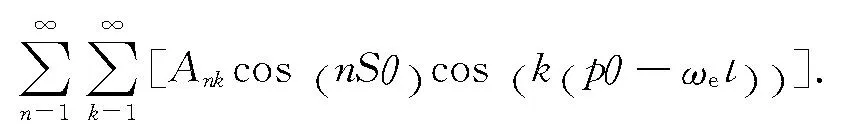
(35)

式中：

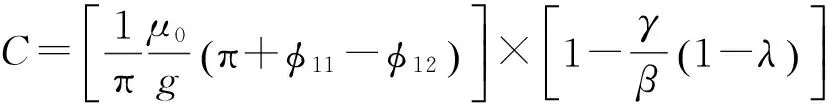
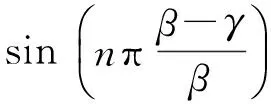
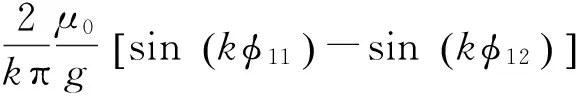
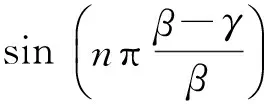
(36)

由式(35)可知,爪極電機氣隙磁導是關于時間t、電機周向位置θ和軸向位置z3個變量的函數(shù).在任意軸向位置z處,氣隙磁導均由以下4部分組成：1)氣隙均勻時的氣隙磁導,為常量；2)單獨由定子開槽引起的氣隙磁導,為周向位置θ的函數(shù)；3)單獨由爪極轉子引起的氣隙磁導,為時間t和電機周向位置θ的函數(shù)；4)由爪極轉子和定子開槽相互作用引起的氣隙磁導,為時間t和電機周向位置θ的函數(shù).

2.4 氣隙磁場

電機氣隙磁場可以由磁動勢和磁導相乘得到.其中轉子勵磁磁場為轉子勵磁磁動勢與氣隙磁導相乘,電樞反應磁場為電樞反應磁動勢與氣隙磁導相乘,忽略磁路飽和,則爪極電機氣隙磁場為轉子勵磁磁場和定子電樞反應磁場的線性疊加.

1)轉子勵磁磁場.

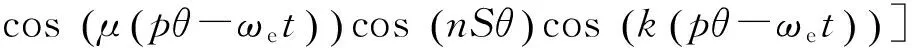
(37)

2)電樞反應磁場.

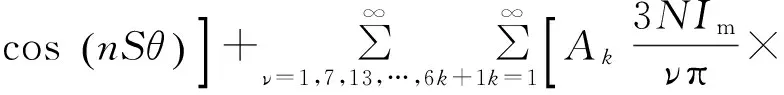
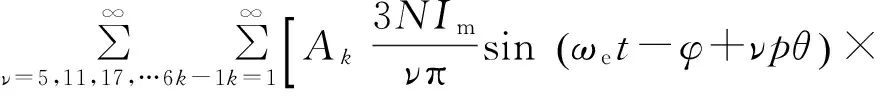
(38)

3)氣隙合成磁場.

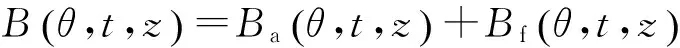
(39)

由上式可知,爪極電機氣隙磁場是關于時間t、電機周向位置θ和軸向位置z3個變量的函數(shù).

對爪極發(fā)電機氣隙磁場的各階磁密幅值和頻率特性進行總結,如表1所示.

3 有限元和試驗驗證

為了驗證上述解析模型的準確性,本文以電勵磁爪極發(fā)電機虛擬樣機為例進行分析.根據(jù)單元電機理論,只要建立該電機的1/6模型進行驗證,其有限元模型如圖8所示,電機具體參數(shù)如表2所示.

根據(jù)爪極發(fā)電機的工作狀態(tài),對虛擬樣機在空載、電樞反應以及負載3種狀態(tài)下分別進行仿真計算,然后提取氣隙中間處(r=49.337 5mm)的徑向磁密分量并將其與解析結果進行對比,如圖9和10所示，其中，Brf為轉子勵磁磁場徑向分量，Bra為電樞反應磁場徑向分量，Br為氣隙合成磁場徑向分量.圖9為t=0時刻,在電機軸向中間位置z=11mm處的徑向氣隙磁密；圖10為t=0.003s時刻,在電機軸向位置z=6mm處的徑向氣隙磁密.由對比結果可知,解析計算結果與有限元結果總體吻合得比較好,證明了該解析模型的準確性.

表1 各階磁密的幅值與頻率特性

Tab.1Amplitudeandfrequencycharacteristicsofeachorderfluxdensity

頻率階次幅值feνp∑∞ν=1,5,7,…6k±1C3NImνπfeνp±nS∑∞ν=1,5,7,…6k±1∑∞n=1An3NIm2νπ()k±1()feν±k()p∑∞ν=1,5,7,…6k±1∑∞k=1Ak3NIm2νπ()k±1()feνp±kp±nS∑∞ν=1,5,7,…6k±1∑∞n=1∑∞k=1Ank3NIm4νπ()μfeμp∑∞μ=1,3,5,…CAμ1∑∞μ=2,4,6,…CAμ2μfeμp±nS∑∞μ=1,3,5,…∑∞n=112Anμ1()∑∞μ=2,4,6,…∑∞n=112Anμ2()μ±k()feμ±k()p∑∞μ=1,3,5,…∑∞k=112AkAμ1()∑∞μ=2,4,6,…∑∞k=112AkAμ2()μ±k()feμp±kp±nS∑∞μ=1,3,5,…∑∞n=1∑∞k=114AnkAμ1()∑∞μ=2,4,6,…∑∞n=1∑∞k=114AnkAμ2()

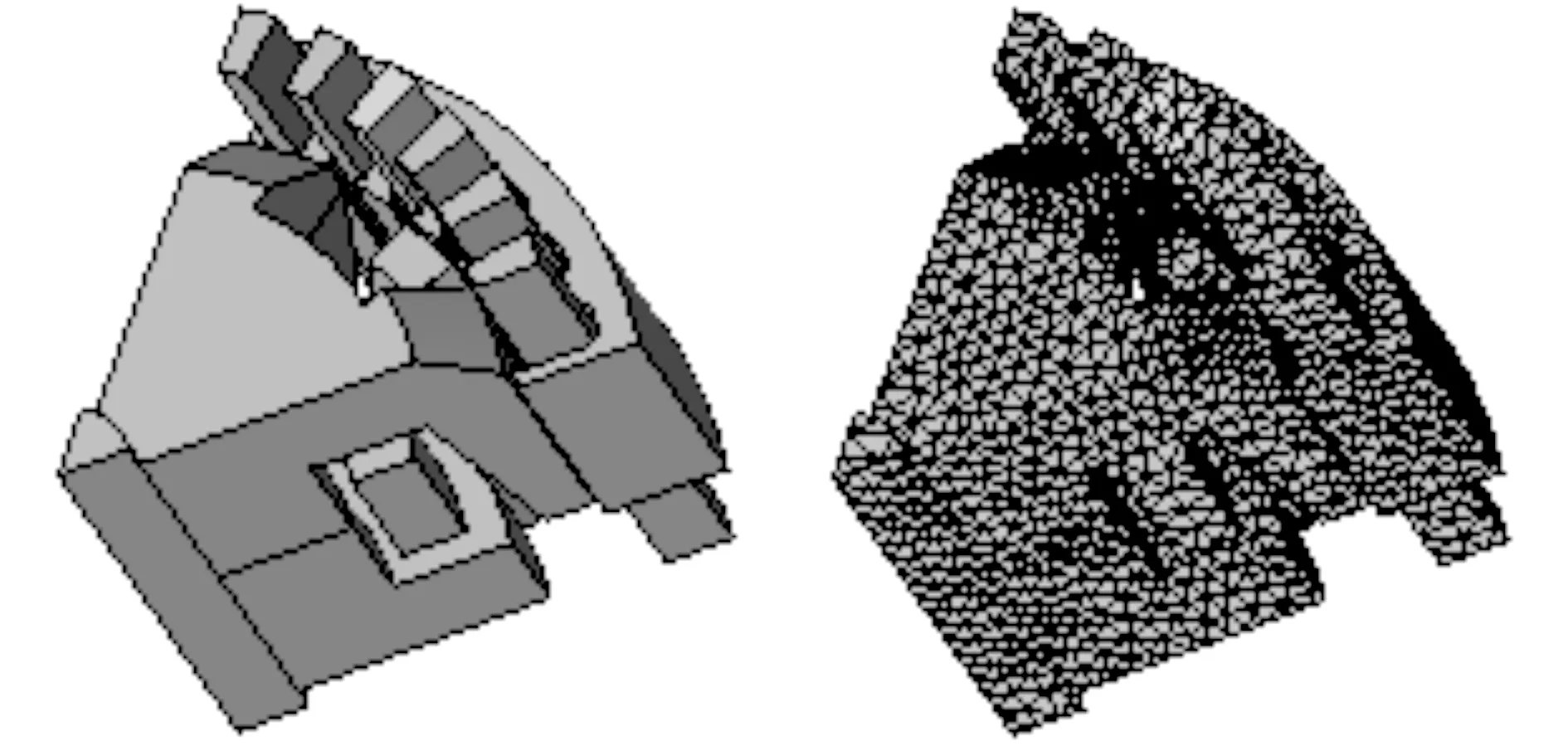
圖8 電勵磁爪極發(fā)電機三維有限元模型Fig.8 3D finite element model of electric excitation claw pole alternator

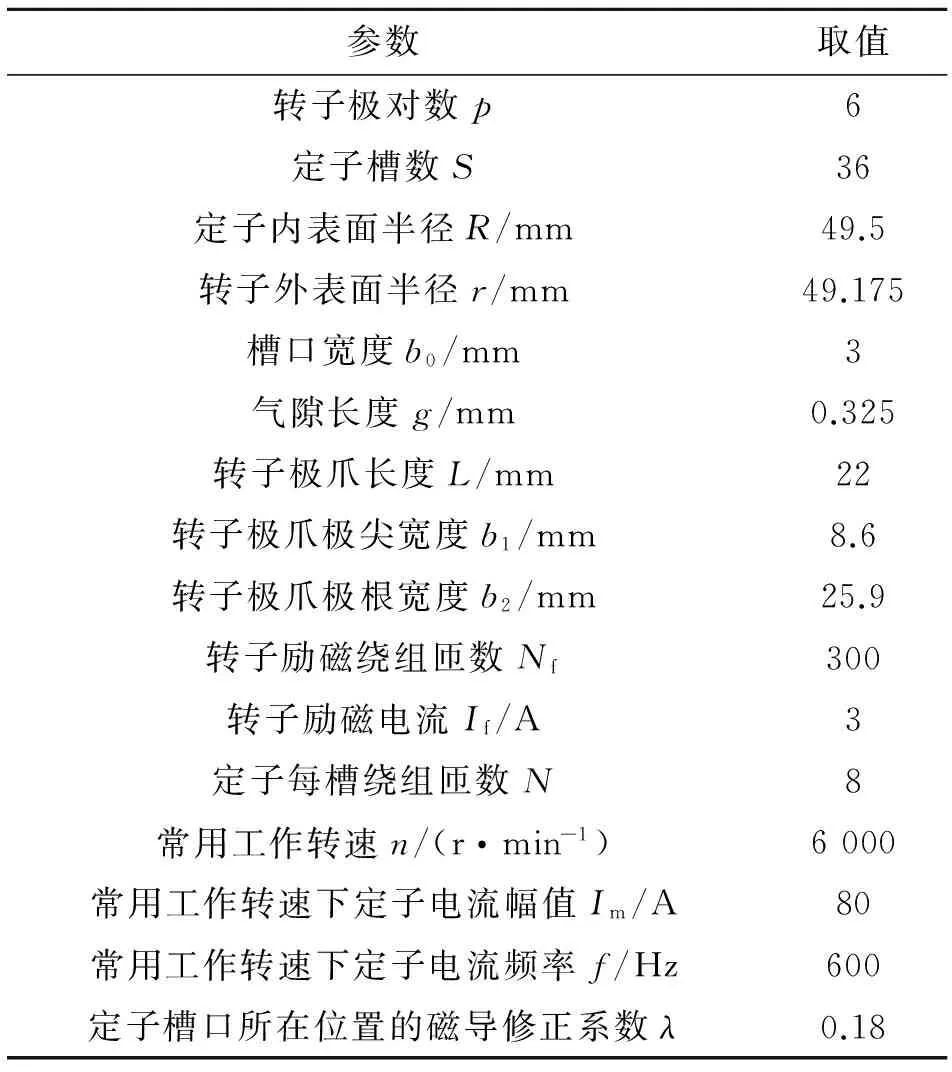
表2 電勵磁爪極發(fā)電機參數(shù)Tab.2 Parameters of electric excitation claw pole alternator

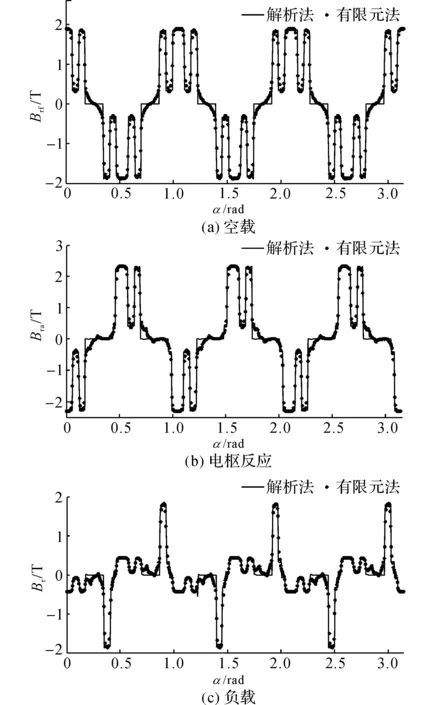
圖9 徑向氣隙磁密(t=0 s, z=11 mm)Fig.9 Radial components of magnetic flux density

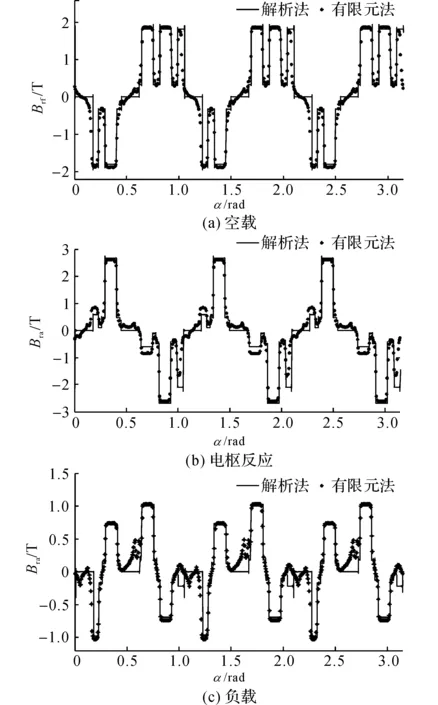
圖10 徑向氣隙磁密(t=0.003 s,z=6 mm)Fig.10 Radial components of magnetic flux density

圖11 負載徑向氣隙磁密空間諧波(t=0 s,z=11 mm)Fig.11 Harmonics of raidal magnetic flux density in load

同時，由圖9和10也可看出，在轉子極爪以及定子齒槽邊緣處解析結果和有限元結果出現(xiàn)了較大的偏差.這主要是由前面的轉子磁導模型引起的,由于爪極電機轉子結構復雜,在這里直接假設轉子極爪間氣隙處的磁導均勻且為0,而氣隙處的磁導實際上是不均勻的,越靠近鐵芯磁導越大.由圖11的諧波分析可知,其中υ為磁場的空間階次.這些誤差并不會明顯改變磁場的空間分布,只是對某些諧波的幅值有一定的影響,并且這些影響很小,幾乎可以忽略不計.

為了進一步驗證本文解析模型的準確性,試驗測量了一臺車用電勵磁爪極發(fā)電機在勵磁電流為3A,轉速為1 500r/min時的反電動勢,測量裝置如圖12所示,并將試驗測量結果與有限元結果進行對比如圖13所示，其中E為反電動勢.從圖13可以看出,有限元結果和試驗測量結果幾乎完全吻合,證明了有限元方法的準確性,從而也間接證明了本文推導的解析模型的準確性.

圖12 反電動勢試驗測量Fig.12 Experimental system to measure the back-EMF

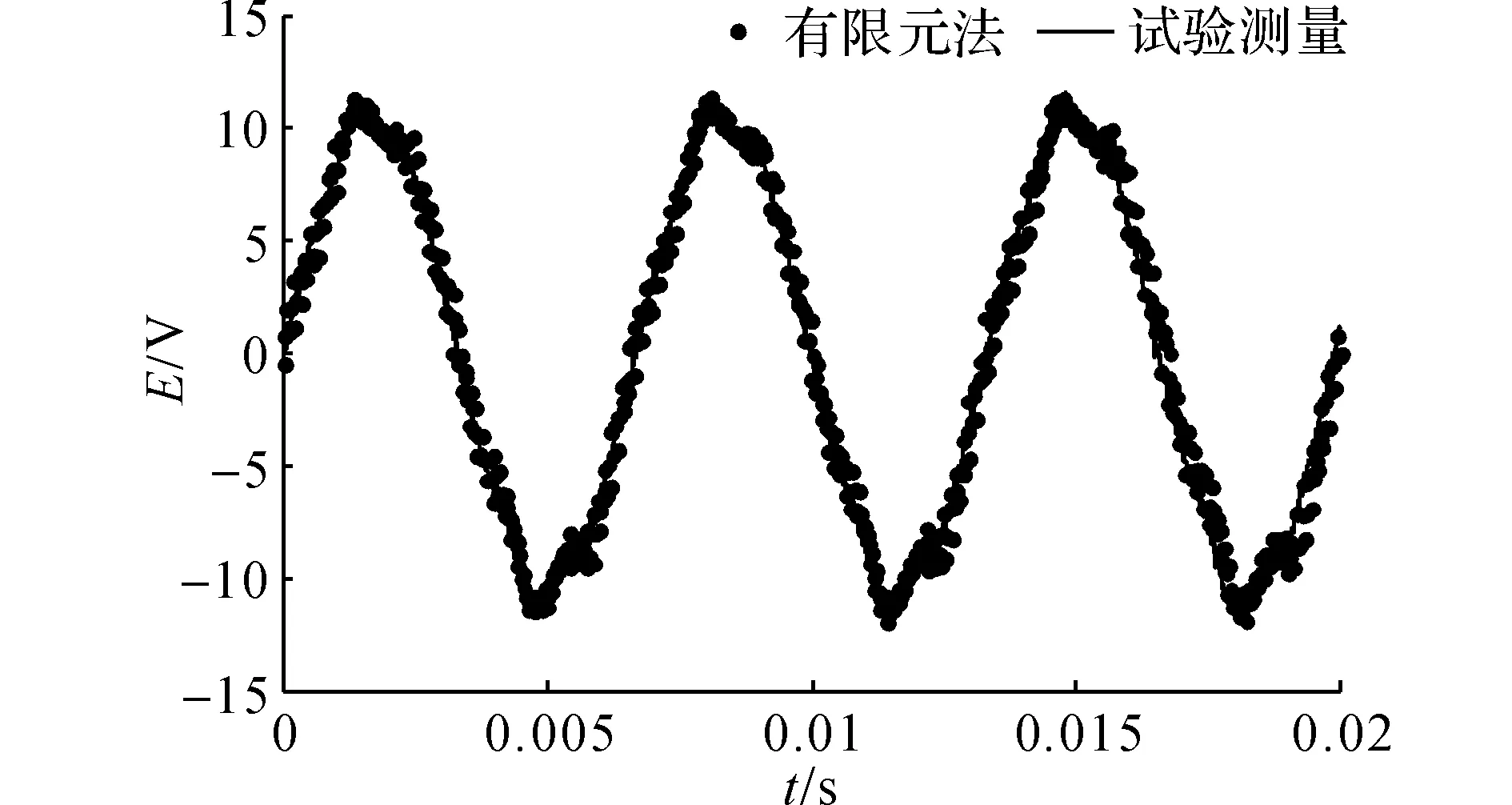
圖13 A相繞組反電動勢Fig.13 Back-EMF of phase A

4 結 語

本文基于磁動勢和氣隙磁導建立了電勵磁爪極發(fā)電機氣隙磁場的解析計算模型,并通過三維有限元法和反電動勢試驗驗證了該模型的準確性.本文的解析模型具有以下幾個特點：

1) 相比耗時的三維有限元法和復雜的等效磁網(wǎng)絡模型,本文的解析模型可以對爪極發(fā)電機的氣隙磁場進行快速準確計算,特別適合用于電機初始設計階段的分析；

2) 可以快速準確計算任意時刻在電機不同軸向位置處空載、電樞反應和負載3種狀態(tài)下的氣隙磁場分布,同時還可以分析磁場諧波的來源及其幅值與頻率特性；

3) 給出了氣隙磁場與電機結構參數(shù)及電磁參數(shù)之間的關系,為爪極電機的性能優(yōu)化奠定了理論基礎.

由于該模型是基于電機定轉子鐵芯磁導率無窮大的假設,下一步可以考慮漏磁和飽和的影響,使模型的準確性進一步提高.

[1]CROSJ,VIAROUGEP.Newstructuresofpolyphaseclaw-polemachines[J].IEEETransactionsonIndustryApplications, 2004, 40(1): 113-120.

[2]REBHIR,IBALAA,MASMOUDIA.Anattempttoimprovethegeneratingcapabilitiesofahybridclawpolemachine[C] ∥ProceedingsofICEMS2011.Beijing:IEEE, 2011: 1-5.

[3]ZHANGFG,ZHANGSF,BAIHJ,etal.Magneticfieldanalysisandperformancecalculationfornewtypeofclawpolemotorwithpermanentmagnetouterrotor[C] ∥ProceedingsofIPEMC2006.Shanghai:IEEE, 2006: 1-5.

[4]LIL,KEDOUSA,FOGGIAA,etal.Influenceofmagneticmaterialsonclawpolemachinesbehavior[J].IEEETransactionsonMagnetics, 2010, 46 (2): 574-577.

[5] 劉光偉,張鳳閣,魏瀚陽,等.外永磁轉子爪極電機空載氣隙磁場解析計算[J]. 電工技術學報,2014, 29(1): 52-59.LIUGuang-wei,ZHANGFeng-ge,WEIHan-yang,etal.Analyticmodelofnoloadairgapmagneticfieldforclawpolemotorwithouterpermanentmagnetrotor[J].TransactionsofChinaElectrotechnicalSociety, 2014,29(1): 52-59.

[6]GUOYG,ZHUJG,LUHY.Accuratedeterminationofparametersofaclaw-polemotorwithSMCstatorcorebyfiniteelementmagnetic-fieldanalysis[J].IEEEProceedings-ElectricPowerApplications, 2006, 153 (4): 568-574.

[7]LIMSB,JUNGDS,KIMKC,etal.Characteristicanalysisofpermanent-magnet-typesteppingmotorwithclawpolesbyusing3dimensionalfiniteelementmethod[J].IEEETransactionsonMagnetics, 2007, 43 (6): 2519-2521.

[8]DOUY,GUOY,ZHUZ,etal.Effectofarmaturereactionofapermanent-magnetclawpoleSMCmotor[J].IEEETransactionsonMagnetics, 2007, 43 (6):2561-2563.

[9]CRISTIANB,CONSTANTINO,CHIVERO,etal.Theadvantagesofnumericalanalysisforclawpolealternator[C] ∥ProceedingsofEPE2014.Lasi:IEEE, 2014: 353-357.

[10]IBALAA,MASMOUDIA.Accountingforthearmaturemagneticreactionandsaturationeffectsinthereluctancemodelofanewconceptofclaw-polealternator[J].IEEETransactionsonMagnetics, 2010, 46 (11): 3955-3961.

[11]REBHIR,IBALAA,MASMOUDIA.MEC-basedsizingofahybrid-excitedclawpolealternator[J].IEEETransactionsonMagnetics, 2015, 51 (1): 211-223.

[12] 喬東偉,王秀和,朱常青.基于等效磁網(wǎng)絡法的新型混合勵磁無刷爪極發(fā)電機的性能計算[J].電機與控制學報,2012, 16(11): 11-16.QIAODong-wei,WANGXiu-he,ZHUChang-qing.Performancecalculationofnovelhybridexcitationbrushlessclaw-polealternatorusingequivalentmagneticcircuitnetworkmethod[J].ElectricMachinesandcontrol, 2012, 16(11): 11-16.

[13] 張鳳閣,劉光偉,白海軍.外永磁轉子爪極電機磁路模型的建立與參數(shù)計算[J].電工技術學報,2012, 27(6): 19-24.ZHANGFeng-ge,LIUGuang-wei,BAIHai-jun.MagneticcircuitmodelandparametercalculationofaclawpolemachinewithouterPMrotor[J].TransactionsofChinaElectrotechnicalSociety, 2012, 27(6): 19-24.

[14]SHENY,ZHUZQ,CHENJT,etal.Analysisofclaw-polerotorbrushlessmachinewithDCexcitationbylumped-parametermagneticcircuitmode[C] ∥ProceedingsofPEDES2012.Bengaluru:IEEE, 2012: 1-6.

[15]IBALAA,REBHIR,MASMOUDIA.Magneticequivalentcircuitbasedmodelingofclawpolemachines:aSurvey[C] ∥ProceedingsofICEMS2011.Beijing:IEEE, 2011: 1-6.

[16]ELLOUMID,IBALAA,REBHIR,etal.DynamicMECmodelingofclawpolealternators[C] ∥ProceedingsofEVER2014.Monte-Carlo:IEEE, 2014: 1-6.

[17]LEESH,KWONSO,LEEJJ,etal.Characteristicanalysisofclaw-polemachineusingimprovedequivalentmagneticcircuit[J].IEEETransactionsonMagnetics, 2009, 45 (10): 4570-4573.

[18] 王群京,倪有源,張學,等.基于三維等效磁網(wǎng)絡法計算混合勵磁爪極發(fā)電機負載特性[J].電工技術學報,2006, 21(6): 96-100.WANGQun-jing,NIYou-yuan,ZHANGXue,etal.Loadcharacteristicscomputationofahybridexcitationclaw-polealternatorusinga3-DMECmethod[J].TransactionsofChinaElectrotechnicalSociety, 2006, 21(6): 96-100.

[19] 王群京,倪有源,李國麗.爪極電機的結構、理論及應用[M].合肥:中國科學技術大學出版社,2006: 40-42.

[20]LUNDMARKS.Applicationof3-Dcomputationofmagneticfieldstothedesignofclawpolemotors[D].Sweden:ChalmersUniversityofTechnology, 2005.

[21]BAIH,PEKAREKS,TICHENORJ,etal.Incorporatingtheeffectsofmagneticsaturationinacoupled-circuitmodelofaclaw-polealternator[J].IEEETransactionsonEnergyConversion, 2007, 22 (2):290-298.

Analytical model of air gap magnetic field for electric excitation claw pole alternators

ZUO Shu-guang, WU Shuang-long, WU Xu-dong, LIN Fu, Deng Wen-zhe

(CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804,China)

A new analytical model was presented to calculate the air gap magnetic field in order to realize the quick computation and analysis of the performance of electric excitation claw pole alternators. Firstly, Fourier series decomposition was applied to compute the no-load air gap magnetomotive force (MMF), armature reaction MMF and air gap permeance. Then, no-load air gap magnetic field and armature reaction field were derived based on the MMF and permeance. Correction factor was introduced to consider the influence of rotor claw shape and stator slots. Finally, 3D finite element analysis and experimental results were presented for verifying the accuracy of the proposed model. The model established the relationship between the air gap magnetic field and motor parameters. It is suitable for fast computation of the magnetic field in the initial design stage and performance optimization of the claw pole alternators.

claw pole alternators; magnetomotive force; permeance; air gap magnetic field; analyticalmodel

2015-04-23.

國家自然科學基金資助項目(51375343)；國家重大科學儀器開發(fā)專項(2012YQ150256).

左曙光(1968—)，男，教授，從事汽車振動與噪聲控制的研究. ORCID: 0000-0002-7403-9341. E-mail: sgzuo@tongji.edu.cn 通信聯(lián)系人：吳旭東，男，助理教授. ORCID: 0000-0003-1066-6183. Email: wuxudong@tongji.edu.cn

10.3785/j.issn.1008-973X.2016.12.021

TM 359.9

A

1008-973X(2016)12-2400-09