構造數學模型妙解三角函數最值
2016-12-16 02:51:06江西省贛州市石城縣石城中學342700
數理化解題研究 2016年22期
關鍵詞:模型
江西省贛州市石城縣石城中學(342700)
黃天揚●
?
構造數學模型妙解三角函數最值
江西省贛州市石城縣石城中學(342700)
黃天揚●
1.構造函數模型
利用函數在某一區間上具有單調性求最值




利用均值不等式等號不成立時,可化為雙勾函數,應用雙勾函數單調性去解決.

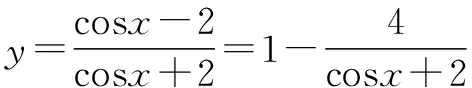
歸納 含有同名的三角函數求最值時,要有意識地將問題的結構特征與函數聯系起來,構造函數模型.
2.構造均值不等式模型
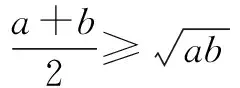
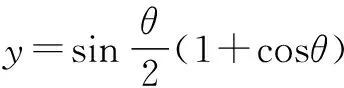
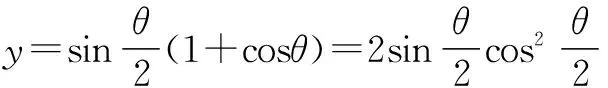
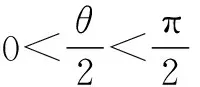
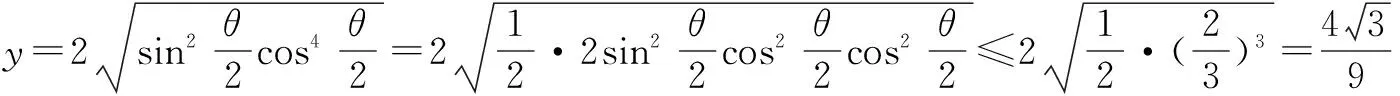
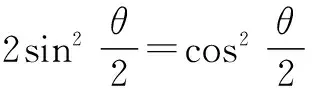
注意:利用均值不等式要觀察等號成立的條件.
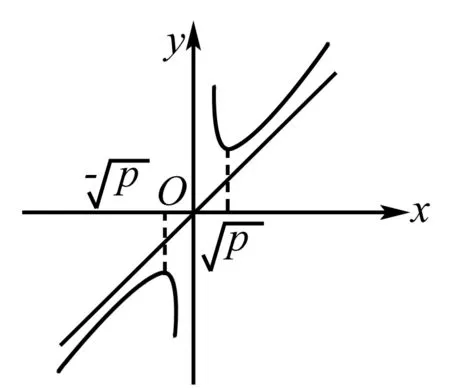
3.構造斜率模型

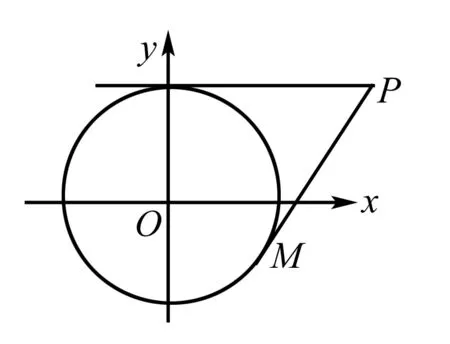
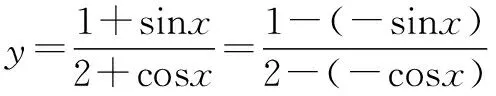
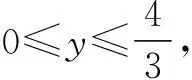
歸納:
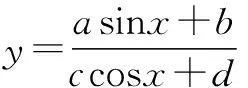
4.構造問題結構的向量模型
由數量積a·b=|a||b|cosθ, 有|a·b|≤|a||b|.
例5 求函數y=sin2x+2sinxcosx+3cos2x的最值.
解 原函數可化為y=2+sin2x+cos2x,所以只須求sin2x+cos2x的最值.設a=(sin2x,cos2x),b=(1,1).
∴|a·b|≤|a||b|,

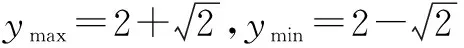
歸納 用向量解三角問題,關鍵在于巧妙地構造向量,為此需要我們有意識地將問題的結構特征與向量的有關運算及表示法聯系起來.
總之,在求三角函數的最值中,靈活運用數學的各種方法,會使問題的解答簡捷,明了.
G632
B
1008-0333(2016)22-0031-01
猜你喜歡
童話王國·奇妙邏輯推理(2024年5期)2024-06-19 16:03:38
網絡安全與數據管理(2022年1期)2022-08-29 03:15:20
導航定位學報(2022年4期)2022-08-15 08:27:00
中學生數理化·中考版(2022年8期)2022-06-14 06:55:24
新世紀智能(數學備考)(2021年9期)2021-11-24 01:14:36
成都醫學院學報(2021年2期)2021-07-19 08:35:14
新世紀智能(數學備考)(2020年9期)2021-01-04 00:25:14
中學生數理化·七年級數學人教版(2020年10期)2020-11-26 08:24:50
數學物理學報(2020年2期)2020-06-02 11:29:24
光學精密工程(2016年6期)2016-11-07 09:07:19

