問診解三角形問題中的幾類高頻錯解
四川省資陽市外國語實驗學校 (641300)
蔡勇全●
?
問診解三角形問題中的幾類高頻錯解
四川省資陽市外國語實驗學校 (641300)
蔡勇全●
解三角形是高中數學教學中的重點和難點,也是歷年高考的必考點和命題熱點,但面對利用正余弦定理或三角函數關系所產生的各類解,學生往往缺乏必要的甄別意識和區分技能,從而造成“會而不對,對而不全”的現象時有發生.本文結合實例辨析解三角形問題中的幾類高頻錯解,供大家參考.
一、忽視三角形三內角關系而致錯

(Ⅰ)求sinB的值;
(Ⅱ)求sin(2B+30°)的值.


評注 “任意三角形中三內角之和必為180°”是求解所有三角形問題時都應重視的一個隱含條件,也往往是解決此類問題的關鍵.
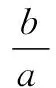

二、忽視三角形角之間的內在制約而致錯
例2 在△ABC中,c=4,C=60°,求△ABC周長的最大值.





評注 三角形角之間的內在制約的前提是上文提到的內角和定理,在此基礎上,如果已知某一個角,那么余下兩角之和必為定值,這就形成了一種制約關系.

三、忽視對解的個數的判斷而致錯

辨析 本題的根本錯因在于忽視了對三角形解的個數的判斷,因為已知兩邊長與其中一邊的對角解三角形可能出現兩解、一解、無解三種情況,因此在利用正弦定理解三角形時要根據解的個數進行判斷以避免出現錯誤.

評注 對三角形解的個數的判斷往往是建立在使用正余弦定理的基礎上,借助邊邊關系影響角角關系或角角關系影響邊邊關系來確定解的個數.

四、忽視三邊關系定理而致錯
例4 已知2a+1,a,2a-1是鈍角三角形的三邊長度,求a的取值范圍.


評注 三邊關系定理“任意三角形中,兩邊之和大于第三邊,兩邊之差小于第三邊”是解三角形問題的隱含條件,也是求解本題的關鍵.
變式 已知銳角三角形的三邊長分別為 1、3、a,求a的取值范圍.
?

五、忽視三角形的內角范圍而致錯
例5 在△ABC中,已知sin2A=sin2B,試判斷此三角形的形狀.
錯解 因為sin2A=sin2B,所以2A=2B,A=B,△ABC為等腰三角形.
辨析 上面由“sin2A=sin2B”到“2A=2B”不是等價轉化,因未考慮三角形中角的范圍而致錯.

評注 任意三角形中,正是因為三內角之和等于180°,所以才會有三個內角均介于0°~180°之間這樣的隱含信息.

G632
B
1008-0333(2016)22-0021-03

