基于鄰域離散度的異常點檢測算法*

沈琰輝，劉華文，徐曉丹，趙建民，陳中育

浙江師范大學 數理與信息工程學院，浙江 金華 321004

基于鄰域離散度的異常點檢測算法*

沈琰輝，劉華文+，徐曉丹，趙建民，陳中育

浙江師范大學 數理與信息工程學院，浙江 金華 321004

SHEN Yanhui,LIU Huawen,XU Xiaodan,et al.Outlier detection algorithm based on dispersion of neighbors.Journal of Frontiers of Computer Science and Technology,2016,10(12)：1763-1772.

異常點檢測在機器學習和數據挖掘領域中有著十分重要的作用。當前異常點檢測算法的一大缺陷是正常數據在邊緣處異常度較高，導致在某些情況下誤判異常點。為了解決該問題，提出了一種新的基于鄰域離散度的異常點檢測算法。該算法將數據點所在鄰域的離散度作為該數據點的異常度，既能有效避免邊緣數據點的異常度過高，又能較好地區分正常點與異常點。實驗結果表明，該算法能夠有效地檢測數據中的異常點，并且算法對參數選擇不敏感，性能較為穩定。

異常點檢測；機器學習；數據挖掘；主成分分析

1 引言

隨著數字化技術的發展，人們收集到的數據越來越多。然而由于儀器故障、信號干擾、反常行為等因素，數據中通常存在異常點。異常點和其余數據點之間存在顯著差異，一方面會干擾特征提取、模式識別等機器學習任務，另一方面又有助于發現信用卡欺詐、基因突變、網絡入侵等異常現象[1-2]。因此，異常點檢測引起了研究學者的廣泛關注。

當前，許多異常點檢測算法通過距離或密度來度量數據點之間的差異性，例如LOF（local outlier factor）算法[3]、LDOF（local distance-based outlier factor）算法[4]等。然而這些算法的主要問題是邊緣數據點的異常度較高，由于某些情況下邊緣數據點并非異常點，這種效應會影響異常點檢測效果。例如對于均勻分布的數據（如圖1），其中并沒有異常點，但是在上述幾個算法下，點A和B的異常度卻高于其他數據點。如果數據是高斯分布的，這種效應還將進一步放大。顯然這種效應對異常點檢測是不利的，因為它會模糊正常點和異常點之間的界限。并且在無監督學習的場景下，由于異常點的個數未知，一個有效的異常點檢測算法不但要適用于含有異常點的數據集，對于不含有異常點的數據集也要給出合理的結果。

為了解決上述問題，本文提出了基于鄰域離散度的異常點檢測算法。該算法將數據點所在鄰域的離散度作為其異常度，因此對于均勻分布的正常數據點，該算法給出的每個數據點的異常度都是相同的，不存在邊緣放大效應。實驗結果顯示，該算法能夠更有效地檢測數據集中的異常點。

本文組織結構如下：第2章介紹了異常點檢測的相關工作；第3章介紹了主成分分析（principal component analysis，PCA）及其與奇異值分解（singular value decomposition，SVD）的關聯；第4章介紹了本文算法的具體原理、算法步驟、算法復雜度以及參數的選擇；第5章將本文算法和其他幾種算法做了對比實驗，分析了算法效果；第6章對全文進行了總結。

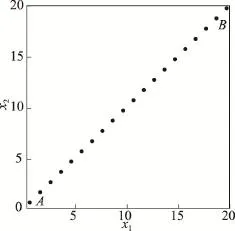
Fig.1 Uniformly distributeddata圖1 均勻分布的數據

2 相關工作

異常點檢測的主要目的是檢測數據集中的少數類，目前已經提出了許多異常點檢測算法。根據模型的不同，大致可以分為基于統計模型的異常點檢測、基于鄰近度的異常點檢測、基于子空間的異常點檢測和基于集成學習的異常點檢測。

基于統計模型的異常點檢測算法早在計算機發明以前就有不少統計學家進行了研究。該模型假設數據在總體上服從某種分布，并將每個數據點與該分布的契合程度作為其異常度，因此這類方法得出的通常是全局意義上的異常點。一種具有代表性的方法是基于深度的異常點檢測算法[5]，它假設數據在空間中是由內到外一層一層包裹而成，通過計算出凸多邊形包圍盒，將數據層層剝離，越處在外層多邊形上的數據點異常度越高，但這種方法對超過三維的數據就不甚理想。近年來，Kriegel等人提出了ABOD（angle based outlier detection）算法[6]。該算法的基本設想是：若某個數據點位于數據分布越稀疏的區域，那么以該點為頂點，任取其余兩個點與該點分別作直線，所形成的個夾角的方差越小。該算法主要優點是無需設置參數，受數據維數的影響較小，然而該算法的時間復雜度為O(dn3)，當數據量很大時，計算開銷難以接受。為此Pham等人提出了FastVOA（fast variance of angles）算法[7]。該算法通過隨機投影和AMS Sketch方法對ABOD算法作近似處理，在一定誤差內，可以將時間復雜度降低到O(n lbn(d+lb2n))。

基于鄰近度的異常點檢測算法側重于尋找局部異常點。這類方法的基本假設是，數據集中可能包含多個數據種類，每類數據的分布性質不同，從全局角度尋找異常點不一定有效。因此這類方法在計算數據點的異常度時，只選擇對應的局部鄰域作為參照集，而不考慮數據的整體分布。這類方法中最具代表性的是基于距離的異常點檢測算法和基于密度的異常點檢測算法。基于距離的異常點檢測算法最早由Knorr等人提出[8-9]，該算法的基本設想是：若某個數據點在半徑為?的區域內的近鄰占總數據點的比例不超過π，則該數據點為異常點。該算法的主要缺點是，實際應用中很難估計參數?。Ramaswamy等人提出了基于k近鄰的算法[10]，該算法將數據點到第k個近鄰的距離作為該點的異常度。基于距離的異常點檢測算法的主要缺陷是，如果數據集同時包含多個密度不同的簇，那么密度較小的簇所包含的數據點容易被誤判為異常點。為了克服此問題，Breunig等人提出了LOF算法[3]。該算法的基本設想是：如果某數據點處的密度低于其鄰域內其他數據點處的平均密度，則該點為異常點，反之則為正常點。該算法的主要問題是對k的取值比較敏感。Kriegel等人提出了LoOP（local outlier probabilities）算法[11]，該算法將LOF算法的思想與概率論相結合，使得算法對帶噪聲的數據更健壯，并且該算法給出的異常度等價于某數據點為異常點的概率，更具有直觀意義。Zhang等人提出了LDOF算法[4]，該算法在某種程度上借鑒了LOF算法相對密度的思想，它把某個數據點到k個近鄰的距離的均值稱作KNN distance，把k個近鄰彼此之間的距離的均值稱作KNN inner distance，然后把這兩種距離的比值作為該數據點的異常度。

傳統的基于鄰近度的異常點檢測算法都會受到“維數災”的影響[12]。為了克服此問題，Agrawal對LOF算法進行了改進[13]，提出了基于局部子空間的異常點檢測算法。該算法的基本設想是：若數據點的近鄰在某個屬性上的方差越小，則在該屬性上越容易發現異常點，應該提高該屬性的權重，因此該算法使用加權歐式距離代替LOF算法中的距離函數。Keller等人通過對數據集在不同子空間內屬性的邊際分布進行研究，發現異常點只有在某些高對比度子空間內才較為顯著，因此提出了HiCS（high contrast subspaces）算法[14]。該算法分兩階段進行：第一階段搜索高對比度子空間，本質上是特征選擇的過程；第二階段在特定的子空間內使用傳統方法進行異常點檢測。實驗結果顯示，基于這一改進的LOF算法在高維數據上的效果有了一定改善。然而這種方法的缺點是搜索子空間較為耗時，并且由于各個數據點所適用的子空間不一定相同，若只用一個子空間會影響各數據點異常度的準確性。Kriegel等人提出了SOD[15]subspace outlier degree）算法和COP[16]（correlation outlier probability）算法，這兩個算法能夠對每個數據點選擇最佳的子空間進行異常度計算，但是算法復雜度較高。

基于集成學習的異常點檢測是近年來出現的一個新的研究熱點。這類方法通過構造多個不同的異常點檢測器，然后合并所有檢測器的輸出，使得檢測效果比任一單個的檢測器更好[17-19]。這類方法的有效性主要取決于3個因素：檢測器本身的準確度，檢測器之間的差異性，如何集成各個檢測器的輸出[20]。

3 PCA

PCA是無監督學習中常用的一種數據分析方法，其主要思想是：在降低數據維數的同時，保持數據中對方差貢獻最大的特征；其基本方法是：通過正交線性變換，將原數據投影到一個新的坐標系統中，使得新數據在各個主分量（principal component，PC）上投影的方差最大化。

更具體地說，假設數據矩陣為X∈?n×d，且每列均值為0。PCA尋求一組標準正交基W=(w1,w2,…,wp)，其中wk∈?d，使得：

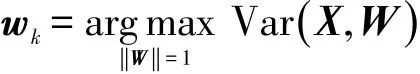
為了求解上式，先將其展開為矩陣形式：

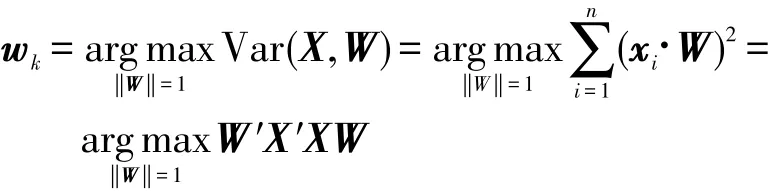
通過拉格朗日乘子法得到：

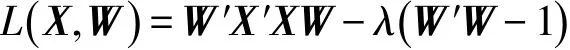
令L(X,W)關于W的偏導數為0，并計算化簡得：

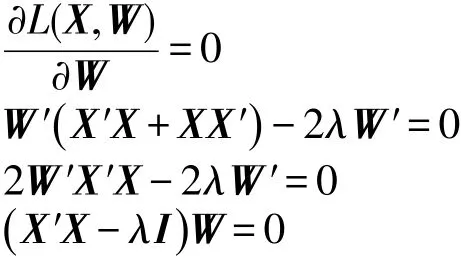
由于X的協方差矩陣Σ=X′X，于是有：

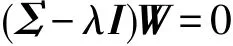
顯然上式是一個特征方程。由于協方差矩陣Σ是實對稱矩陣，能夠對其對進行特征分解，所得的特征向量即為標準正交基，各個特征值即為方差。

然而在實際計算中，為了保證數值穩定性，PCA通常借助奇異值分解來實現。奇異值分解指的是把矩陣X分解為如下形式：

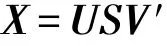
其中，U為n×n階正交矩陣，每列稱為左奇異值向量；V為d×d階正交矩陣，每列稱為右奇異值向量；S為n×d階對角矩陣，對角線上的元素Sij稱為奇異值。將協方差矩陣Σ按奇異值分解的方式展開：

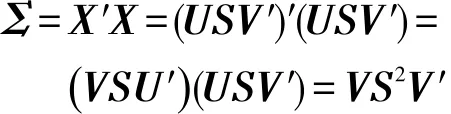
可見PCA所求的標準正交基W就是矩陣X的右奇異值向量V，對應的方差就是矩陣X的各個奇異值的平方。因此直接對矩陣X進行奇異值分解就能間接實現PCA，無需通過計算協方差矩陣然后對其特征分解來實現。

4 基于鄰域離散度的異常點檢測算法

4.1 離散度

一般而言，數據中的異常點分布較為稀疏，正常點較為密集，如圖2所示。為了便于討論數據點在局部空間內的分布情況，本文先給出鄰域的定義。

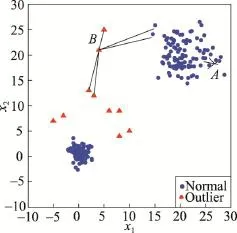
Fig.2 Data contaminated with outliers圖2 含異常點的數據

定義1（鄰域）對于數據點xi∈?d，若其k階近鄰依次為，其中。則稱點集為數據點xi的鄰域，點集為數據點xi的去心鄰域。

在一定的k取值下，正常點的鄰域主要包含其他正常點以及少量噪聲點，因此正常點的鄰域所占空間較小，鄰域較為緊致；而異常點的鄰域包含其他異常點甚至正常點，因此異常點的鄰域所占空間較大，數據點在該空間內的離散度較高。如圖2所示，正常數據點A的去心鄰域都是正常點，異常數據點B的去心鄰域既包含正常點也包含其他異常點。利用這一特性，只要度量各個數據點所在鄰域的離散度，就能實現異常點檢測。

可見本文對離散度的定義本質上等同于跡范數（trace norm），因而。根據文獻[21]的證明，矩陣的跡范數具有以下性質：

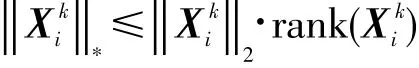
該性質表明，跡范數的上界是譜范數與秩的乘積。若跡范數越大，則譜范數或秩越大，說明構成鄰域的數據點較為離散；若跡范數越小，則譜范數和秩都較小，說明鄰域在整體上較為緊致。因此定義2能夠有效地刻畫鄰域的離散度。

為了進一步驗證定義2對正常點和異常點的區分能力，本文對圖2所示的數據集做了初步的實驗：取k=5，分別計算正常點和異常點的鄰域離散度，然后將離散度視為隨機變量，通過核密度估計分別繪制出相應的概率密度函數。最終如圖3所示，其中藍色實線代表正常點的鄰域離散度概率密度函數，紅色虛線代表異常點的鄰域離散度概率密度函數，可見兩個分布的重疊部分較小，因此定義2能夠有效區分正常點和異常點。

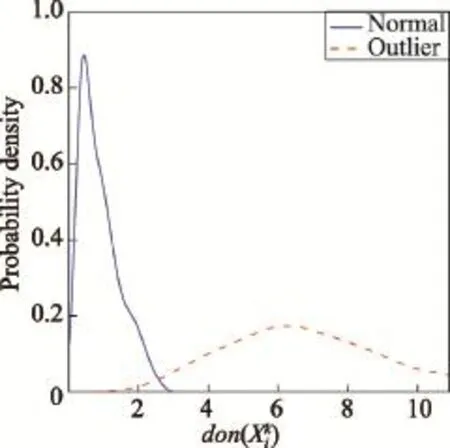
Fig.3 Probability density function of dispersion圖3 離散度的概率密度函數

4.2 基于鄰域離散度的異常點檢測算法

由前文的討論可知，正常點的鄰域離散度較小，而異常點的鄰域離散度較大，通過計算數據點所在鄰域的離散度，就能得知該數據點的異常度。因此，本文對數據點的異常度定義如下。

定義3（異常度）數據點xi的異常度即為該點所在的k階鄰域的離散度。若某個數據點的異常度越高，則該數據點越有可能是異常點。

根據上述定義，通過計算每個數據點的異常度，按數值高低進行排序，最后輸出異常度最高的t個數據點，就可以實現異常點檢測。具體算法如下：

算法1 DON算法

本算法通過一次循環就能完成。對每個數據點來說，主要的計算量在于兩部分：第一部分是尋找數據點xi的k近鄰，通過使用k-d樹[22]作為數據結構，查詢k近鄰的時間復雜度為O(dnlbn)。第二部分是對鄰域做主成分分析，由于主成分分析是基于奇異值分解實現的，時間復雜度為O(min(kd2,k2d))。因此當k的取值不超過數據維數時，每個數據點的計算復雜度與維數的關系仍然是線性的。

參數k的選取對算法效果有著最直接的影響。由定義1可知，當k=n時，任意數據點所在鄰域等同于整個數據集X，因此鄰域的離散度等同于整個數據集的離散度，算法將失去區分能力，從而k的選取并不是越大越好。事實上，如果整個數據集落在m維（m＜d）的低維流形上，那么任意局部鄰域的有效維數m′都不會超過m，這就意味著取k=m就足以刻畫大部分正常點所在鄰域的特性。而確定整個數據集的有效維數可以通過對整個數據集做主成分分析來確定，如果前m個主成分的可解釋變異量（explained variance）足夠高，就可以舍棄其余主成分，認為數據集的有效維數是m。

參數t的選取也十分重要。在實際的應用場景中，由于沒有Ground Truth，無法得知真實異常點的個數，但是可以通過統計的方法估計t的大小。設正常點的異常度為隨機變量Y1，異常點的異常度為隨機變量Y2，所有數據點的異常度為隨機變量Y。若Y1與Y2均服從高斯分布，那么Y就服從混合高斯分布：

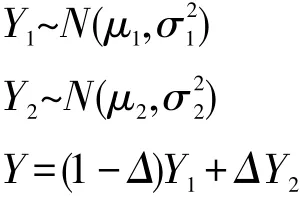
其中Δ∈{0,1},Pr(Δ=1)=π。通過EM算法[23]，給定適當的初始值和收斂條件，經過數次迭代就能求出隱變量π，即為異常點的比例，因此可以取。

5 實驗

5.1 實驗設置

實驗采用UCI數據集[24]，具體屬性如表1所示。其中Iris、Wine數據集由3種類別的樣本構成，因此將其中一類數據進行采樣，使其所占比例低于10%，并標記為異常點。

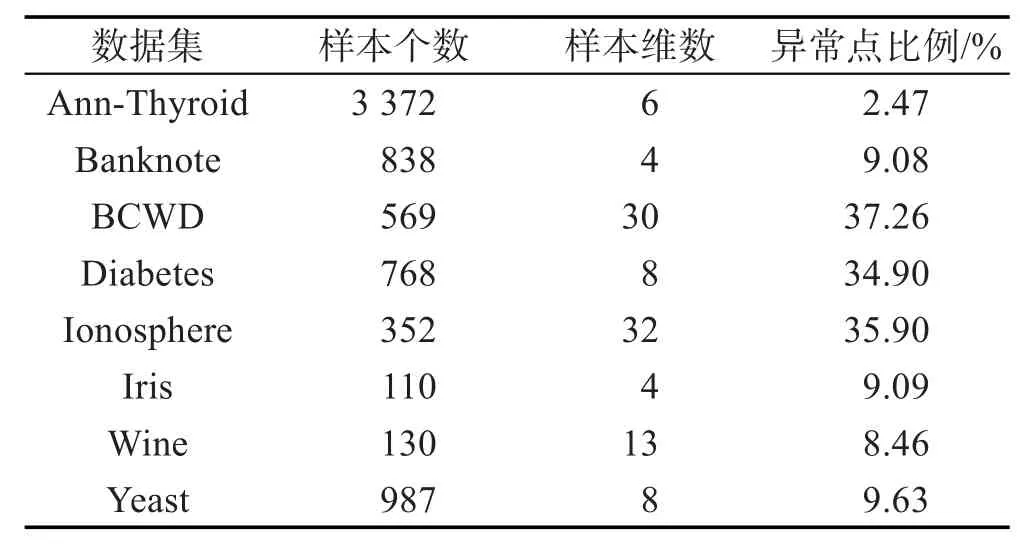
Table 1 Properties of dataset表1 數據集屬性

為了驗證本文算法的有效性，將DON算法與其他幾種流行的異常點檢測算法進行對比，這些算法分別是LOF算法[3]、LDOF算法[4]、LoOP算法[11]、HiCS算法[14]、SOD算法[15]。其中LOF和LoOP是基于密度的異常點檢測算法，LDOF是基于距離的異常點檢測算法，HiCS和SOD是基于子空間的異常點檢測算法。這幾種算法的實現均來自于ELKI數據挖掘框架[25]。

由于所有對比算法本質上都是依據數據點的局部鄰域來計算異常度，對算法效果影響最大參數是k。因此本實驗對所有算法分別取k=5,6,…,100進行測試。對于SOD算法，根據文獻中的建議[15]，實驗將參數l設置為k，α設置為0.8。

5.2 評價標準

為了更好地對比各個算法在不同參數下的檢測效果，本文采用AUC（area under curve）作為評價標準。AUC指的是ROC（receiver operating characteristic）曲線下方的面積，而ROC曲線的參數式方程如下：

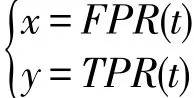
假設所有數據點為集合D，真實異常點為集合G，算法輸出的前t個異常度最高的數據點為集合S(t)，則TPR(t)和FPR(t)的計算公式如下：

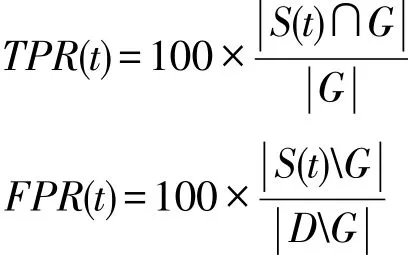
5.3 實驗結果與分析

各個算法在不同k值下的AUC如圖4所示。

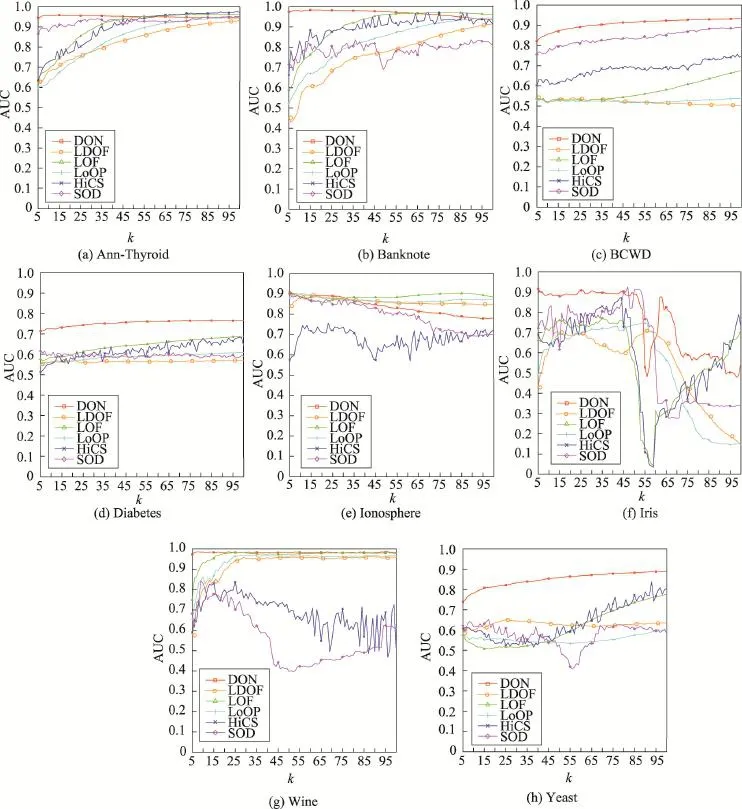
Fig.4 AUC trends with differentksettings of DON,LDOF,LOF,LoOP,HiCS,SOD圖4 k取不同值時DON、LDOF、LOF、LoOP、HiCS、SOD算法的AUC變化

對于Ann-Thyroid、Banknote兩個數據集來說（如圖4（a）、（b）），DON算法在k增大時，AUC呈現出一定的降低趨勢，但總體來說AUC仍然維持在0.9以上，算法比較穩定。SOD算法的AUC波動也不大，但是在各種k取值下，算法有效性均不及DON算法。而其余的算法在k≥100之后，AUC才趨于穩定。因為隨著k值增大，算法運行時間也越長，而且對無監督學習來說，算法在實際應用時沒有Ground Truth，難以調整算法參數，所以相比之下DON算法具有一定優勢。

對于BCWD、Diabetes、Yeast數據集來說（如圖4（c）、（d）、（h）），由于這3個數據集的異常點比例在30%以上，取較大的k值才能刻畫數據點的局部特性。因此大部分算法的AUC總體上隨著k的增大而增大，但是DON算法的AUC高于其他算法，并且曲線走勢較為穩健。

對于Ionosphere數據集來說（如圖4（e）），DON算法在k≤30時效果較好，之后呈現出下降趨勢。LOF和LDOF算法在k=5附近取得最好效果，之后也逐漸下降。而LoOP算法則在k≥85附近才取得最好效果。HiCS算法總體上效果不佳，而且波動較大。

對于Iris數據集來說（如圖4（f）），大部分算法在k＞50之后，AUC開始顯著下降。考慮到該數據集由兩種數量為50的正常點以及10個異常點構成，當k＞50時，正常點的鄰域必然包含異常點或是另一類別的數據點，導致正常點的異常度增大，與真實異常點之間的區分度降低，因此AUC的下降是合理的。

對Wine數據集來說（如圖4（g）），DON算法在取不同的k時AUC較高，且波動較小。而LOF、LDOF、LoOP算法則在k≥25之后，AUC才逐漸趨于穩定。相比之下，HiCS、SOD算法的表現不太理想，尤其是k≥25之后，AUC嚴重降低。

綜上分析，DON算法在7個數據集上都取得了較好的效果，在不同參數下表現也較為穩定，AUC基本不會隨著k值的變化出現較大波動。

6 總結與未來工作

本文提出了一種新的基于鄰域離散度的異常點檢測算法，該算法能夠有效克服正常數據在邊緣處異常度過高的問題。實驗結果表明，本文算法能夠更有效地檢測數據集中的異常點，并且對參數選擇不敏感，性能較為穩定。進一步的工作包括分析本文的異常點定義與其他文獻中的異常點定義之間的內在聯系，研究使用集成學習的方式進一步提高異常點檢測的準確率。

[1]Yang Chao,Chen Guoliang,Shen Yifei.Outlier analysis for gene expression data[J].Journal of Computer Science and Technology,2004,19(1):13-21.

[2]Prakobphol K,Zhan J.A novel outlier detection scheme for network intrusion detection systems[C]//Proceedings of the 2008 International Conference on Information Security and Assurance,Busan,Korea,Apr 24-26,2008.Piscataway,USA: IEEE,2008:555-560.

[3]Breunig M M,Kriegel H P,Ng R T,et al.LOF:identifying density-based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data,Dallas,USA,May 15-18,2000.New York:ACM,2000: 93-104.

[4]Zhang Ke,Hutter M,Jin Huidong.A new local distancebased outlier detection approach for scattered real-world data [C]//LNCS 5476:Proceedings of the 13th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining,Bangkok,Thailand,Apr 27-30,2009.Berlin,Heidelberg:Springer,2009:813-822.

[5]Johnson T,Kwok I,Ng R T.Fast computation of 2-dimensional depth contours[C]//Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining, New York,Aug 27-31,1998.Menlo Park,USA:AAAI,1998: 224-228.

[6]Kriegel H P,Shubert M,Zimek A.Angle-based outlier detection in high-dimensional data[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Las Vegas,USA,Aug 24-27,2008.New York:ACM,2008:444-452.

[7]Pham N,Pagh R.A near-linear time approximation algorithm for angle-based outlier detection in high-dimensional data[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing,Aug 12-16,2012.New York:ACM,2012:877-885. [8]Knorr E M,Ng R T.A unified approach for mining outliers [C]//Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining,Newport Beach, USA,Aug 14-17,1997.Menlo Park,USA:AAAI,1997: 219-222.

[9]Knorr E M,Ng R T.Algorithms for mining distance-based outliers in large datasets[C]//Proceedings of the 24rd Inter-national Conference on Very Large Data Bases,New York, Aug 24-27,1998.San Francisco,USA:Morgan Kaufmann Publishers Inc,1998:392-403.

[10]Ramaswamy S,Rastogi R,Shim K.Efficient algorithms for mining outliers from largedata sets[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data,Dallas,USA,May 15-18,2000.New York: ACM,2000:427-438.

[11]Kriegel H P,Kr?ger P,Schubert E,et al.LoOP:local outlier probabilities[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management,Hong Kong, China,Nov 2-6,2009.New York:ACM,2009:1649-1652.

[12]Beyer K,Goldstein J,Ramakrishnan R,et al.When is“nearest neighbor"meaningful?[C]//LNCS 1540:Proceedings of the 7th International Conference on Database Theory,Jerusalem,Israel,Jan 10-12,1999.Berlin,Heidelberg:Springer, 1999:217-235.

[13]Agrawal A.Local subspace based outlier detection[C]//Proceedings of the 2nd International Conference on Contemporary Computing,Noida,India,Aug 17-19,2009.Berlin,Heidelberg:Springer,2009:149-157.

[14]Keller F,Muller E,Bohm K.HiCS:high contrast subspaces for density-based outlierranking[C]//Proceedings of the 2012 IEEE 28th International Conference on Data Engineering, Arlington,USA,Apr 1-5,2012.Piscataway,USA:IEEE, 2012:1037-1048.

[15]Kriegel H P,Kr?ger P,Schubert E,et al.Outlier detection in axis-parallel subspacesof high dimensional data[C]//Proceedings of the 13th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining,Bangkok,Thailand,Apr 27-30,2009.Berlin,Heidelberg:Springer,2009: 831-838.

[16]Kriegel H P,Kr?ger P,Schubert E,et al.Outlier detection in arbitrarily oriented subspaces[C]//Proceedings of the 12th IEEE International Conference on Data Mining,Brussels, Belgium,Dec 10-13,2012.Piscataway,USA:IEEE,2012: 379-388.

[17]LazarevicA,Kumar V.Feature bagging for outlier detection [C]//Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago,USA,Aug 21-24,2005.New York:ACM,2005: 157-166.

[18]Liu F T,Ting K M,Zhou Zhihua.Isolation-based anomaly detection[J].ACM Transactions on Knowledge Discovery from Data,2012,6(1):3.

[19]Zimek A,Gaudet M,Campello R J,et al.Subsampling for efficient and effective unsupervised outlier detection ensembles[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago,USA,Aug 11-14,2013.New York:ACM,2013: 428-436.

[20]Zimek A,Campello R J,Sander J,Ensembles for unsupervised outlier detection:challenges and research questions a position paper[J].ACM SIGKDD Explorations Newsletter, 2013,15(1):11-22.

[21]Fazel M.Matrix rank minimization with applications[D]. Serra Mall,Stanford,USA:Stanford University,2002.

[22]Arya S,Mount D M,Netanyahu N S,et al.An optimal algorithm for approximate nearest neighbor searching fixed dimensions[J].Journal of theACM,1998,45(6):891-923.

[23]Hastie T,Tibshirani R,Friedman J.The elements of statistical learning[M].New York:Springer,2001:272-282.

[24]Lichman M.UCI machine learning repository[Z].2013.

[25]Achtert E,Kriegel H P,Zimek A.ELKI:a software system for evaluation of subspace clustering algorithms[C]//LNCS 5069:Proceedings of the 20th International Conference on Scientific and Statistical Database Management,Hong Kong, China,Jul 9-11,2008.Berlin,Heidelberg:Springer,2008: 580-585.

SHEN Yanhui was born in 1987.He is an M.S.candidate at Zhejiang Normal University.His research interests include machine learning and data mining,etc.

沈琰輝（1987—），男，江蘇宜興人，浙江師范大學碩士研究生，主要研究領域為機器學習，數據挖掘等。

LIU Huawen was born in 1977.He received the Ph.D.degree in computer science from Jilin University in 2010. Now he is an associate professor at Zhejiang Normal University.His research interests include data mining and machine learning,etc.

劉華文（1977—），男，江西樂安人，2010年于吉林大學獲得計算機博士學位，現為浙江師范大學副教授，主要研究領域為數據挖掘，機器學習等。發表學術論文20余篇，其中SCI檢索13篇，主持或承擔過多項國家自然科學基金、浙江省自然科學基金、中國博士后基金和國家重點實驗室開放項目等。

XU Xiaodan was born in 1978.She is a lecturer at Zhejiang Normal University.Her research interests include machine learning and data mining,etc.

徐曉丹（1978—），女，浙江東陽人，浙江師范大學講師，主要研究領域為機器學習，數據挖掘等。發表學術論文10余篇，主持或參與過多項浙江省自然科學基金、浙江省教育廳項目等。

ZHAO Jianmin was born in 1950.He received the M.S.degree in computer science from Zhejiang University in 2000.Now he is a professor and Ph.D.supervisor at Zhejiang Normal University.His research interests include machine learning,cloud computing and Internet of things,etc.

趙建民（1950—），男，上海人，2000年于浙江大學獲得碩士學位，現為浙江師范大學教授、博士生導師，主要研究領域為機器學習，云計算，物聯網等。發表學術論文50余篇，主持或承擔過多項國家自然科學基金、浙江省自然科學基金重大項目、國家公安部項目等。

CHEN Zhongyu was born in 1965.He received the Ph.D.degree in computer science from Shanghai University in 2010.Now he is a professor at Zhejiang Normal University.His research interests include machine learning and data mining,etc.

陳中育（1965—），男，浙江浦江人，2010年于上海大學獲得計算機博士學位，現為浙江師范大學教授，主要研究領域為機器學習，數據挖掘等。發表學術論文30余篇，主持或承擔過多項國家自然科學基金、浙江省自然科學基金、浙江省科技廳重點項目等。

Outlier DetectionAlgorithm Based on Dispersion of Neighbors*

SHEN Yanhui,LIU Huawen+,XU Xiaodan,ZHAO Jianmin,CHEN Zhongyu
College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua,Zhejiang 321004,China
+Corresponding author:E-mail:hwliu@zjnu.edu.cn

Outlier detection is an important task of machine learning and data mining.A major limitation of the existing outlier detection methods is that the outlierness of border points may be very high,leading to yield misleading results in some situations.To cope with this problem,this paper proposes a novel outlier detection algorithm based on the dispersion of neighbors.The proposed algorithm adopts the dispersion of a data point's neighbors as its outlier degree, thus the outlierness of border points will not be very high while the normal data and outliers can still be well distinguished.The experimental results show the proposed algorithm is more effective in detecting outliers,less sensitive to parameter settings and is stable in terms of performance.

outlier detection;machine learning;data mining;principal component analysis

10.3778/j.issn.1673-9418.1509075

A

TP181

*The National Natural Science Foundation of China under Grant Nos.61272007,61272468,61572443(國家自然科學基金);the Natural Science Foundation of Zhejiang Province under Grant No.LY14F020012(浙江省自然科學基金);the Foundation of Zhejiang Educational Committee under Grant No.Y201328291(浙江省教育廳項目).

Received 2015-07,Accepted 2015-09.

CNKI網絡優先出版:2015-10-20,http://www.cnki.net/kcms/detail/11.5602.TP.20151020.1041.002.html