基于星載高速調制器的射頻功放線性化技術研究

向 前,李惠媛,楊津浦

(上海航天電子技術研究所,上海201109)

?

基于星載高速調制器的射頻功放線性化技術研究

向 前,李惠媛,楊津浦

(上海航天電子技術研究所,上海201109)

為補償射頻功放非線性失真對高速寬帶數傳系統的影響，對全數字基帶預失真算法進行了研究和改進。用Matlab仿真工具對預失真的最小均方(LMS)、遞歸最小二乘(RLS)算法進行了分析和比較，提出了一種新的變步長迭代收斂算法。在接收端對調制的中頻信號直接采樣，無需采集發端數據，用寬帶鎖相環和相關峰技術實現收、發信息同步，對整個信道的線性和非線性失真進行補償處理。仿真表明該算法可提高預失真的性能和收斂速度。在星載高速調制器和行波管功放系統中對改進算法后的預失真技術進行了測試，16QAM寬帶信號驗證結果表明該方案可提高系統性能，減小功放非線性對系統的影響。

星載高速數據傳輸； 寬帶數字預失真； 非線性失真； 調制器； 線性化； 變步長迭代收斂

0 引言

隨著遙感衛星及其有效載荷技術的發展，航天器產品獲取的信息量和數據量出現了突飛猛進的增長，對提高星地傳輸速率的需求尤為迫切。為滿足未來星地高速數據傳輸要求，擴大對地觀測衛星的應用領域，解決寬帶信號頻率資源緊張問題，研究高頻帶利用率的高階調制數傳技術有重要意義[1]。高階調制的高速數傳系統中，采用的16QAM，32APSK等高階調制方式具非恒定包絡調制的特性，星載行波管功放(TWTA)或固態功放(SSPA)的線性化技術是衛星高速數傳研究的關鍵技術瓶頸[2]。信道的非線性對高階調制信號產生頻譜擴展、星座圖扭曲和非線性碼間干擾等不利影響，嚴重降低了高速數據傳輸系統的性能[3]。為消除信道中非線性器件(功率放大器、行波管放大器等)對信號造成的非線性失真，需針對通道設計預失真補償算法，根據非線性器件實測指標的特點，設計高速、寬帶和低復雜度的預失真算法，完成數字預失真功能仿真與硬件實現，并最終完成性能的優化，以及在高速數據傳輸系統中的應用[4]。

在高速數傳射頻通道補償中，采用自適應均衡方法消除信道的線性失真，可減少對非線性預失真方案的影響，并在此前提下對通道內非線性失真進行補償。傳統的數字預失真算法在求解相關參數時，采用收、發同源的閉環鏈路實現載波同步，但在星載航天器高速寬帶的數傳系統中，由于星載寬帶高速接收解調設備較復雜，高速解調不適于航天器使用，只能在地面實現，很難實現收、發同源。如前饋法方案有較寬的補償工作帶寬，但需額外的輔助補償放大器，且要求此輔助放大器自身的預失真特性應與被補償放大器互補，技術難度較大，實現效率較低；安捷倫公司的數字預失真(DPD)硬件測試系統，發端的信號發生器必須單獨送一路10 MHz參考時鐘至收端的信號分析設備，以保持收、發載波同步，但星載數傳設備不可能單獨向地面提供一路載波時鐘信號。本文對星載高速寬帶數據傳輸系統提出一種寬帶數字預失真方案，在接收端對調制后的中頻信號直接采樣，無需采集發端數據，采用寬帶鎖相環和相關峰技術實現收、發信息同步，對整個信道的線性和非線性失真做補償處理，求出其通道失真的補償系數，利用Matlab的Simulink平臺和高速硬件FPGA資源實現高速數據傳輸系統的預失真技術。

1 鏈路補償方案設計

高速數據傳輸系統的射頻通道如圖1所示。根據射頻通道的器件特性劃分信道的線性失真區和非線性失真區。高速數字預失真算法可補償由放大器、行波管功放等產生的非線性失真。

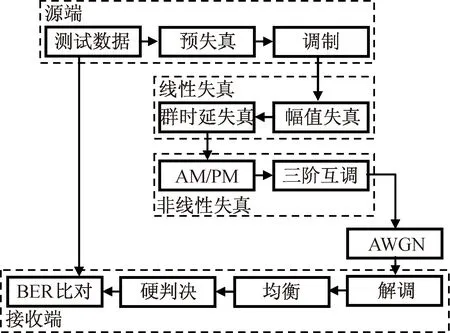
圖1 高速數傳發射機射頻通道Fig.1 RF channel in high-speed data transmitter

源端包括數據生成模塊、映射模塊、預失真模塊和調制模塊，可實現測試數據的產生、預失真和調制；信道模擬包括線性失真模塊(含幅值和群時延失真)、非線性失真模塊(含AM/PM和三階互調效應)和AWGN模塊，可模擬衛星傳輸信道，添加幅值失真、群時延失真，以及由TWTA造成的AM/PM效應和三階互調效應，之后添加高斯白噪聲；接收端包括解調模塊、均衡模塊、硬判決模塊和BER比對模塊，實現數據的接收、解調、均衡、判決及最后的誤碼率比對[5]。因16QAM較16PSK有4 dB的信噪比增益，綜合考慮頻帶利用率、功率效率和實現復雜度，本文采用16QAM作為高階數傳傳輸調制方式。

2 預失真算法分析

本文預失真算法用于高速數傳通信系統。在寬帶應用中，功放的記憶效應變得尤為明顯，功放輸出不再是輸入信號的即時函數，而與過去的輸入有關，這嚴重影響通信系統的正常傳輸，此時無記憶預失真就不再適用[6]。綜合考慮兼顧算法復雜度和寬帶信號的算法性能，選用有記憶性的記憶多項式模型作為預失真模型[7]。

2.1 預失真參數求解

經典記憶多項式模型可表示為

(1)

式中：x(n)為輸入信號；z(n)為輸出信號；K，Q分別為非線性的階數和記憶深度；akq為模型系數[8]。令Z為預失真器輸出矢量，A為預失真系數矢量，U為預失真器輸入矢量，則式(1)可表示為

Z=UA.

(2)

式中：

U=[XnXn+1…Xn+l-1]T；

(3)

Z=

[z(n)z(n+1) …z(n+l-1)]T.

(4)

此處：

Xn=

[X1…Xq…Xq(k-1)-1…Xqk].

(5)

其中：X1=x(n)|x(n)|0；X2=x(n-1)|x(n-1)|0；Xq=x(n-q)|x(n-q)|0；Xq(k-1)=x(n)|x(n)|k-1；Xq=x(n-q)|x(n-q)|k-1。

用LMS和RLS算法識別預失真系數。

2.1.1 基于LMS迭代的預失真算法

以n=0，1，2，…，L-1為一組的輸入序列，若預失真模型經測試和驗證在多項式階數為k、記憶深度為q時性能最佳，則預失真系數的個數m=kq[9-10]。LMS步驟如下：

a)初始化wm(0)=0；

d)系數矢量更新wm(n+1)=wm(n)+μU′lm(n)e(n)。

式中：μ為步長因子，用于控制穩定性和收斂速度，一般0<μ<2/λmax；wm為m維預失真系數向量；U為經功放記憶效應后的輸入信號矩陣；e(n)為第n個輸入數據的誤差值。此處：λmax為輸入序列自相關矩陣的最大特征值。

2.1.2 基于RLS迭代的預失真算法

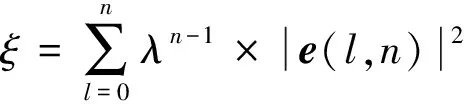
d)計算卡爾曼增益矢量

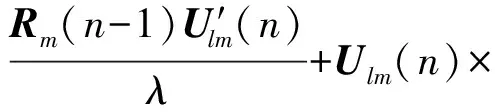
e)更新相關矩陣的逆

Rm(n)=(Rm(n-1)-Kml(n)Ulm(n)×Rm(n-1))/λ；

在整個醫學檢驗質量控制工作中，醫學檢驗人員發揮著至關重要的作用，其是實現醫學檢驗高質量、高效率的基礎。但是就目前來看，很多醫療機構內的檢驗人員在進行醫學檢驗的時候，很容易會出現疏忽大意的情況，沒有對醫學檢驗質量進行嚴格的控制，從而導致醫學檢驗質量大幅下降，使檢驗結果的準確性得不到有效的保障。

f)系數矢量更新

wm(n+1)=wm(n)+Kml(n)el(n).

式中：δ為很小的正數；Rm為信號(估計)相關矩陣的逆；Im為對Rm初始化的單位陣。

由此可知：LMS中系數矢量的更新為wm(n+1)=wm(n)+μU′lm(n)e(n)，μ是唯一可變參數；RLS中系數增益變量是誤差乘以增益向量Km(n)，而Km(n)為M維，因此每個系數都被增益向量的1個元素調整，算法的收斂更快。

2.2 預失真算法改進

對LMS而言，當步長較大時，權系數會加快收斂速度向最佳系數靠攏，而步長較小時，權系數會以較慢的速度向權系數平穩靠攏，步長選取直接影響LMS的性能。對LMS算法進行仿真研究了步長的影響，發現即使在通過迭代收斂后，不同組的預失真系數對系統的影響仍有較大差距，這說明求最佳預失真系數的算法還不夠穩定。本文提出一種簡單的算法修正算法中的步長因子，變步長μ(n)的更新可表示為

w(n+1)=w(n)+μ(n)e(n)U(n).

(6)

式中：U(n)為輸入預失真器的信號矩陣；μ(n)e(n)·U(n)=Δw(n)為濾波權系數矢量迭代更新的調整量。為實現快速收斂，須合適選擇μ(n)的值，常用的方法有多種，多是將步長構造為隨迭代次數而變的函數，再進行仿真分析。但類似的構造方法不易獲得預失真系數的最佳值，因為函數本身的局限性和復雜性導致需求的參數較難選取。本文用簡單易實現的分區間設定步長的方法提高收斂性能，具體方法如下。設經原迭代算法驗證的最佳步長為μopt(0<μopt<2)，迭代總次數為Ntot，則

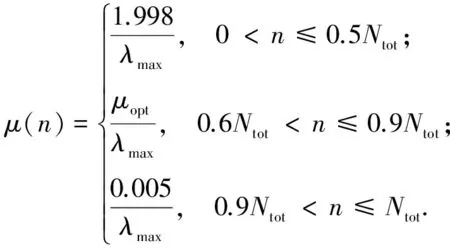
(7)

采用的λmax為經驗值，可根據實際需求調整其大小，原則是先用大步長使算法盡快收斂，再用適中步長繼續收斂至平穩，最后用較小步長細化增量，實現穩態收斂。該法靈活性大，可根據需要細化分段區間。仿真驗證該法在不改動原算法的基礎上，通過細化分段區間替換步長可使經預失真后的帶外抑制提高約3 dB，這是因為由原算法所得系數并非最佳值，改進算法可更接近最優系數，而預失真對系數選取較敏感，因此提升了預失真的非線性補償效果。

3 預失真方案仿真實現

3.1 預失真方案的Matlab仿真

本文仿真的發射端用M文件編寫了高階調制的發射序列，接收端采用了Simulink中頻仿真程序。將調制后的中頻信號直接采樣送接收端處理，用寬帶鎖相環和相關峰技術實現收發信息同步。因高速率數據傳輸受采樣率限制，且實際應用中發送端經功放后均經過帶通濾波器進行濾波，故不考慮信號帶寬遠端的頻譜帶外抑制，主要分析近端(3倍帶寬內)的頻譜特性。

LMS算法的數據跟蹤結果分別如圖2、3所示。由圖可知：LMS算法在約400個數據點后開始收斂，收斂后數據跟蹤良好。由圖2可發現，收斂后的誤差波動較大，而預失真系統對模型系數較敏感，需進一步提高算法收斂后的穩定性，使系數隨迭代達到最優值。由圖3可發現，LMS算法使經過預失真器的實際輸出值與理想的期望值間誤差較小，說明了算法的正確性。但須在全部迭代中選取一組最佳系數，因此局部的數據吻合并不能使整體的數據效果達到最佳，要求使算法能更穩定地收斂于系數最優解。

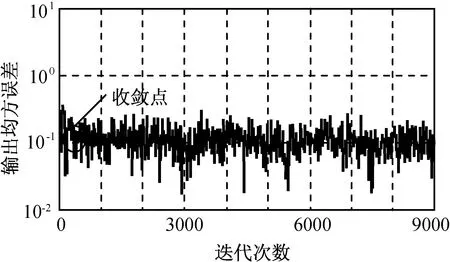
圖2 LMS算法的誤差收斂Fig.2 Error converging performance of LMS algorithm

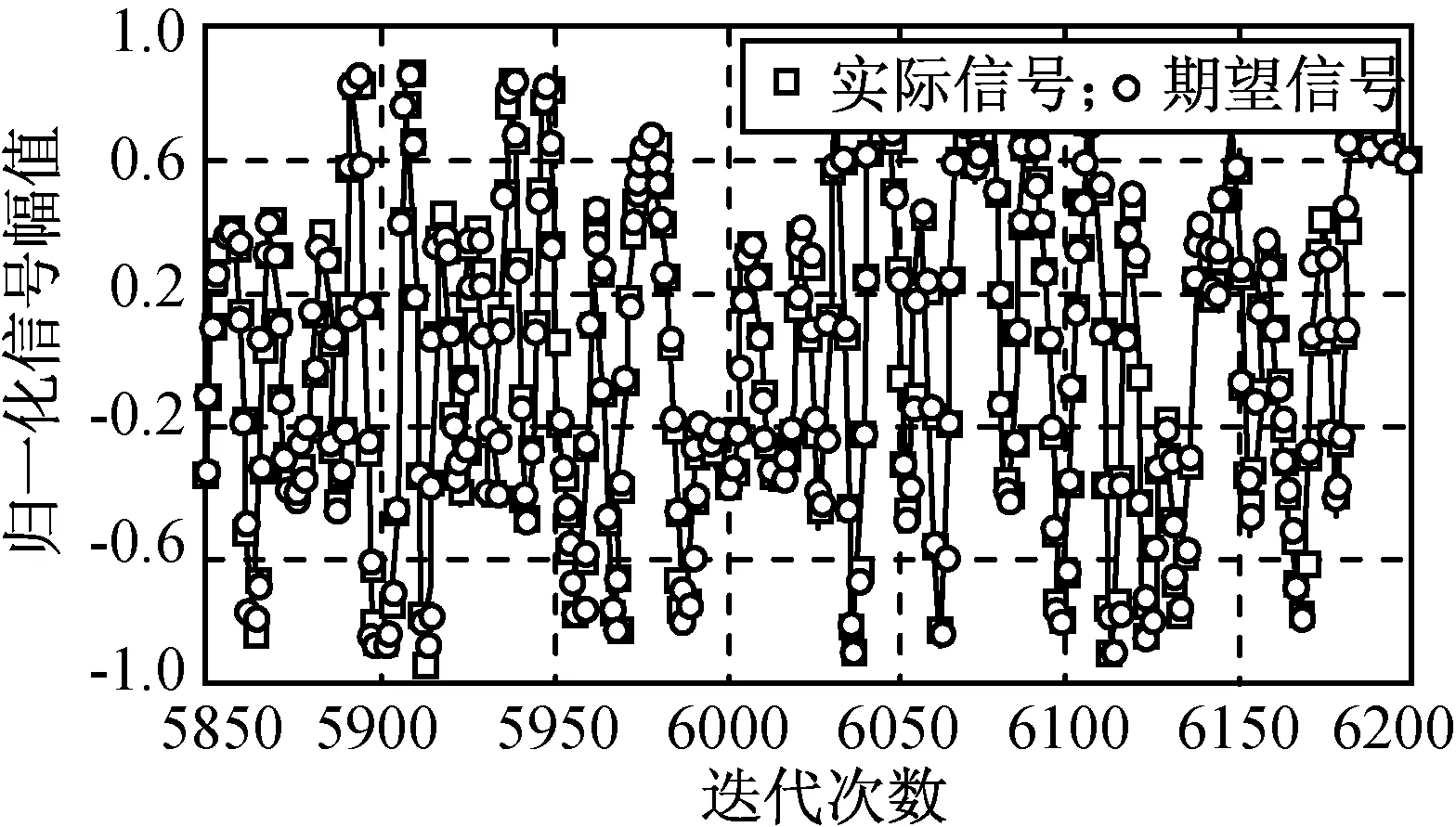
圖3 LMS算法的數據跟蹤Fig.3 Data tracking performance of LMS algorithm

RLS算法的數據跟蹤結果分別如圖4、5所示。由圖可知：RLS算法在100個數據點內開始收斂，收斂后數據跟蹤良好。仿真結果如前文所述，RLS算法中系數更新受m維元素的控制，其收斂較LMS算法更快。除收斂速度較快外，RLS算法的誤差收斂結果和實際信號與期望信號間的吻合性與LMS算法接近。

圖4 RLS算法的誤差收斂Fig.4 Error converging performance of RLS algorithm

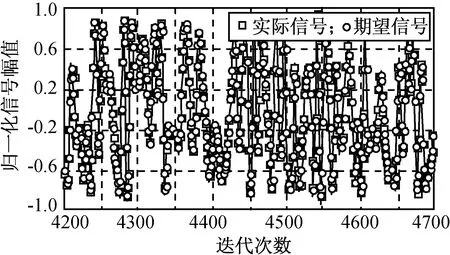
圖5 RLS算法的數據跟蹤Fig.5 Data tracking performance of RLS algorithm

原始信號與經功放的信號，以及用LMS，RLS算法求解的預失真后頻譜如圖6所示。由圖6可知：LMS算法仿真求出的預失真系數可使系統帶外抑制提高17.5 dB，而經RLS算法仿真求出的預失真系數可使系統帶外抑制提高17.1 dB，兩者間并無明顯差別。雖然預失真對功放的非線性給予了明顯的補償，但與理想信號相比仍有提高余地。

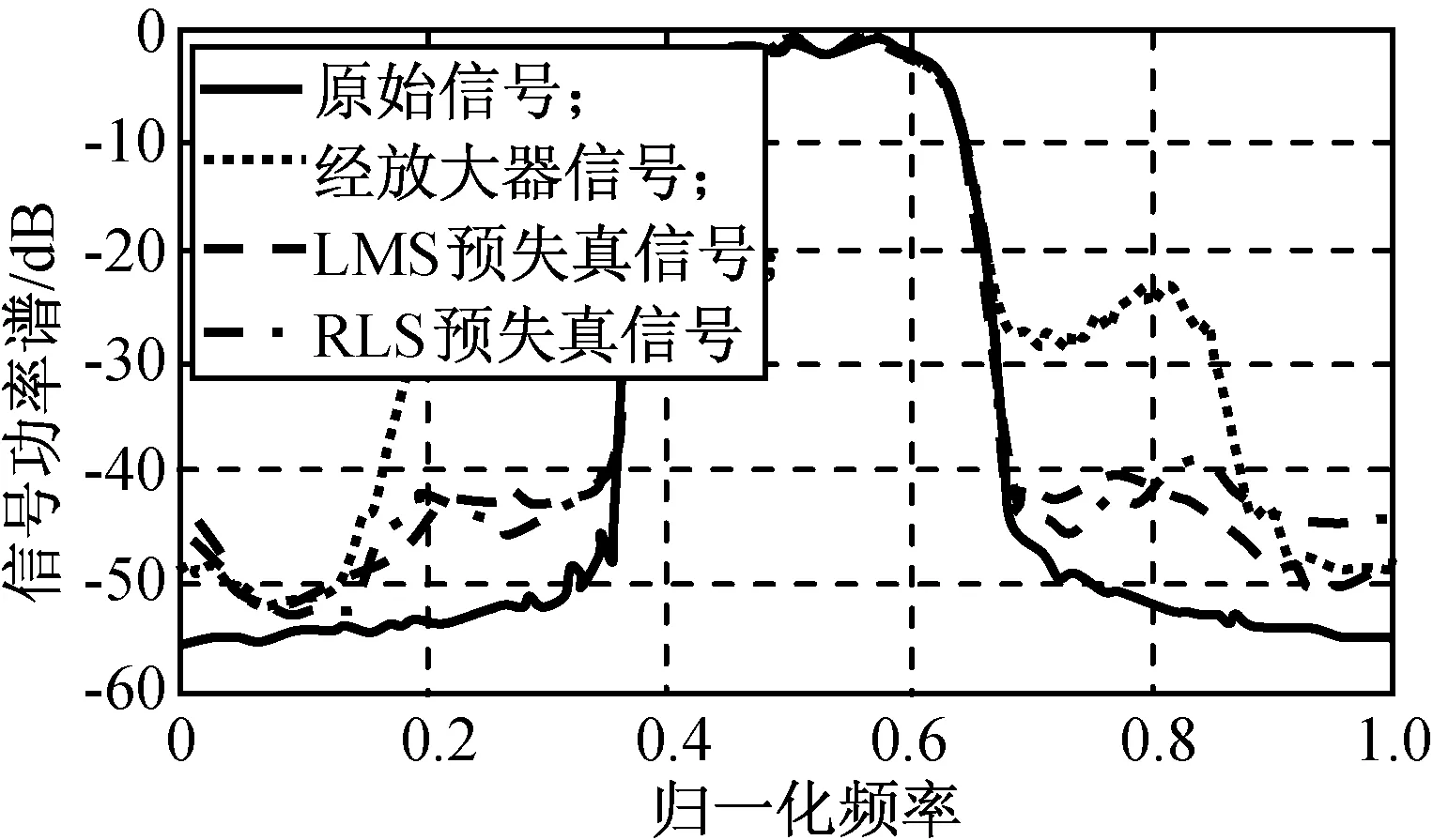
圖6 LMS，RLS算法性能Fig.6 Performance analysis of LMS and RLS algorithms

變步長改進后的算法與原LMS算法比較如圖7～9所示。由圖7、8可知：經預失真所得的實際信號與理想信號幾乎完全重合，誤差非常小且收斂平穩。由圖9可知：改進后算法的帶外抑制較LMS算法高3 dB，這是因為改進后的算法在開始時采用了大步長快速收斂于穩定狀態，以提高收斂速度，之后采用原算法最佳步長在過渡區間繼續收斂并平穩，最后在剩余區間內用較小步長穩定收斂性能，使收斂后誤差波動達到最小，更接近于最優解，預失真系統達到更優的補償狀態。

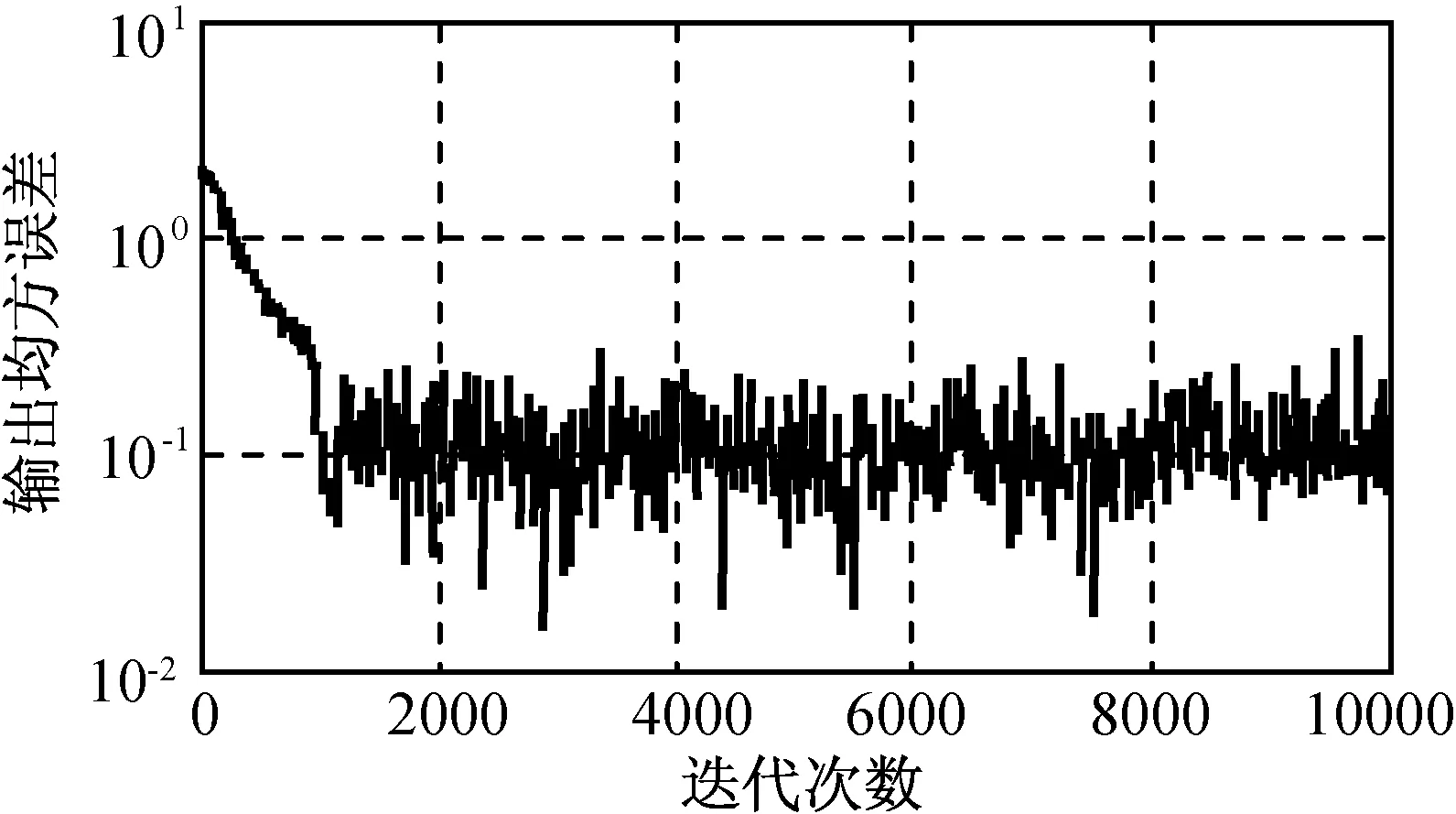
圖7 變步長改進算法誤差收斂Fig.7 Error converging performance of modified LMS algorithm with variable step

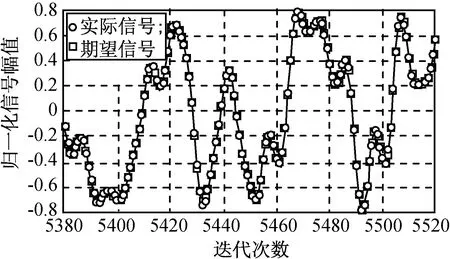
圖8 變步長改進算法數據跟蹤Fig.8 Data tracking performance of modified LMS algorithm with variable step

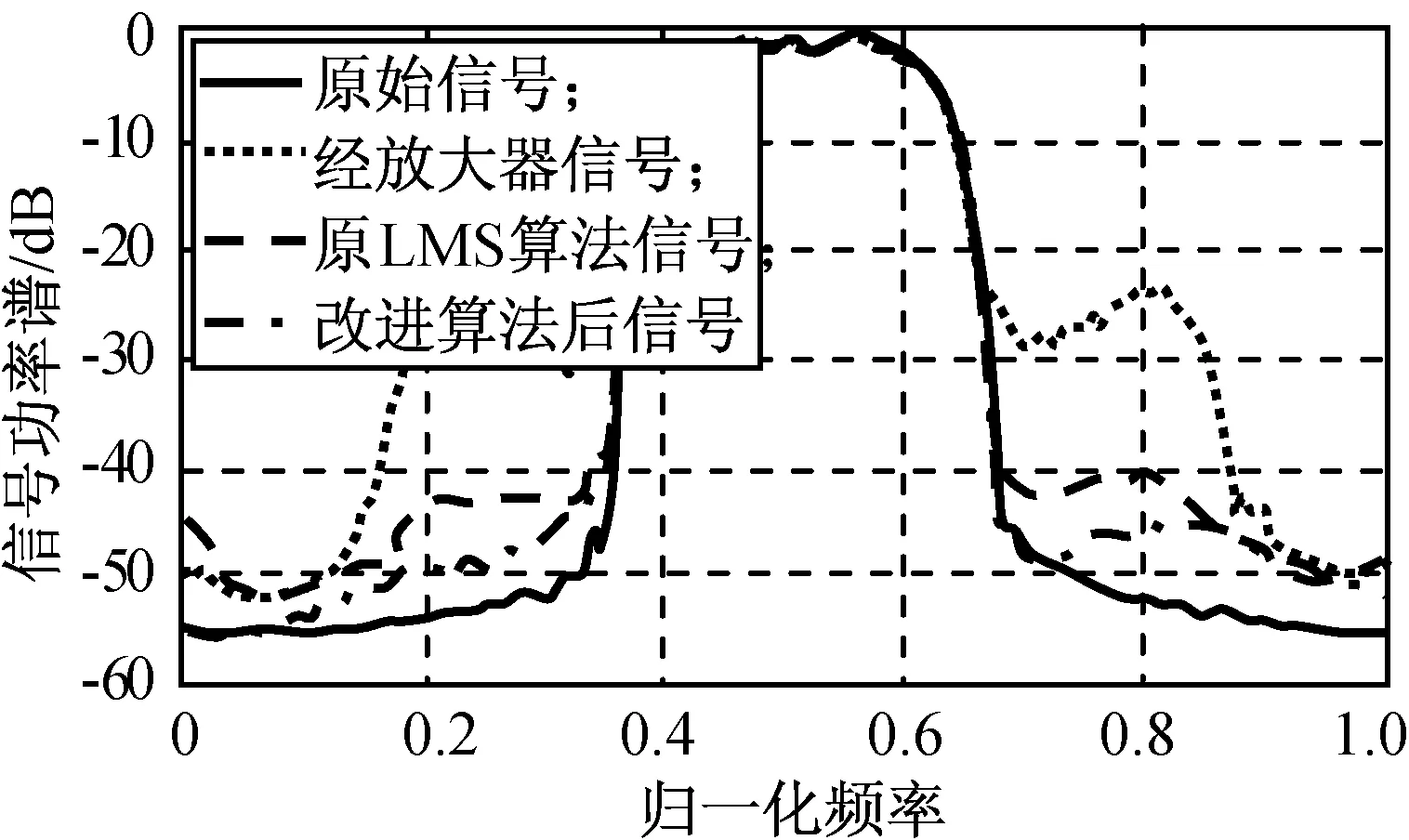
圖9 變步長改進算法與LMS算法性能Fig.9 Performance of LMS and modified algorithms

3.2 改進算法預失真實測結果

為驗證算法在實際應用中可行性，將設計的高速數字預失真算法用于高速數傳發射系統。該測試系統主要由星載高速調制器、星載50 W飽和輸出行波管功放、下變頻器和中頻高速解調器組成。

功放的非線性會導致系統性能出現兩方面的惡化，一是在帶外產生頻譜擴散，產生鄰信道干擾，二是在帶內產生失真，致使系統的EVM和信噪比性能下降，繼而使系統誤碼率性能下降[11]。本文采用16QAM調制方式，平方根升余弦，滾降系數0.5，實測單通道數據傳輸速率2 Gb/s，調制帶寬750 MHz。將行波管功放的輸出功率推至接近飽和區的非線性區域，取輸入回退功率(IBO)-3 dB，在Ka頻段測試，測試結果見表1、2和如圖10～13所示。

由圖10、12可知：未加數字預失真的調制信號在經過行波管放大器后出現了幅值失真，星座圖扭曲(AM/AM，AM/PM效應)，同時非線性器件引起的三階交調失真導致信號的頻譜出現了起伏，這樣的信號在接收端難以正常解調，系統誤碼率性能大幅降低。

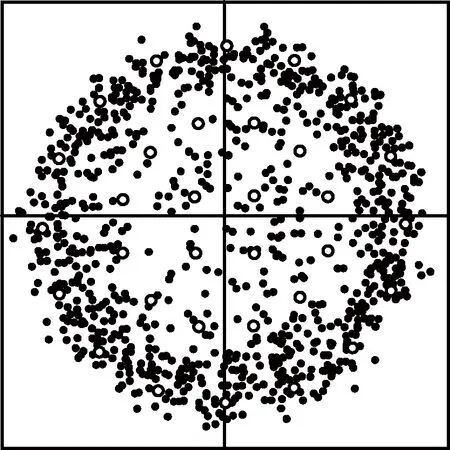
圖10 未加預失真星座圖測試結果Fig.10 Constellation of system without pre-distortion

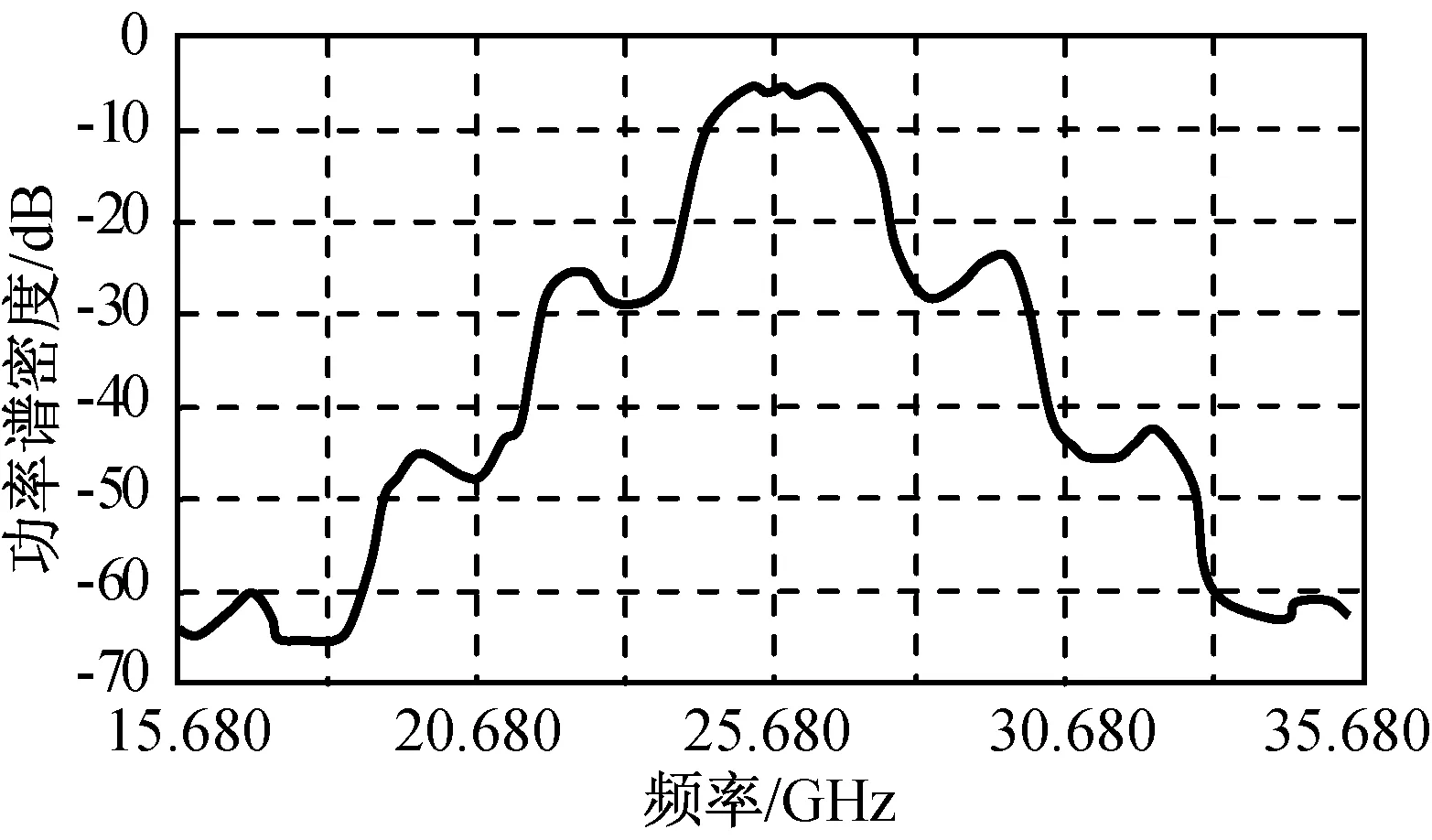
圖12 未加預失真的頻譜測試結果Fig.12 Spectrum performance of system without pre-distortion

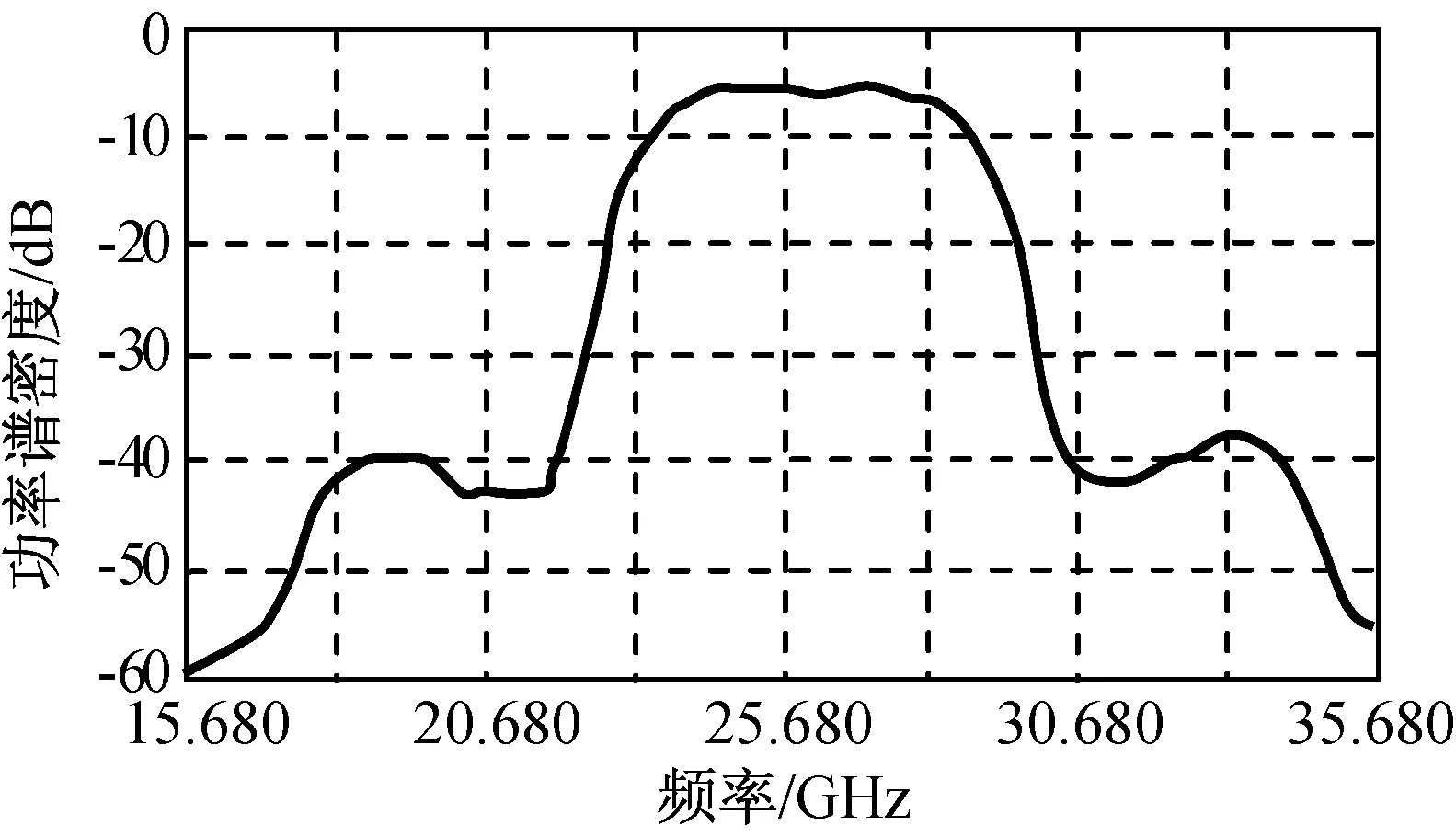
圖13 加改進算法后的預失真頻譜測試結果Fig.13 Spectrum performance of system with modified pre-distortion

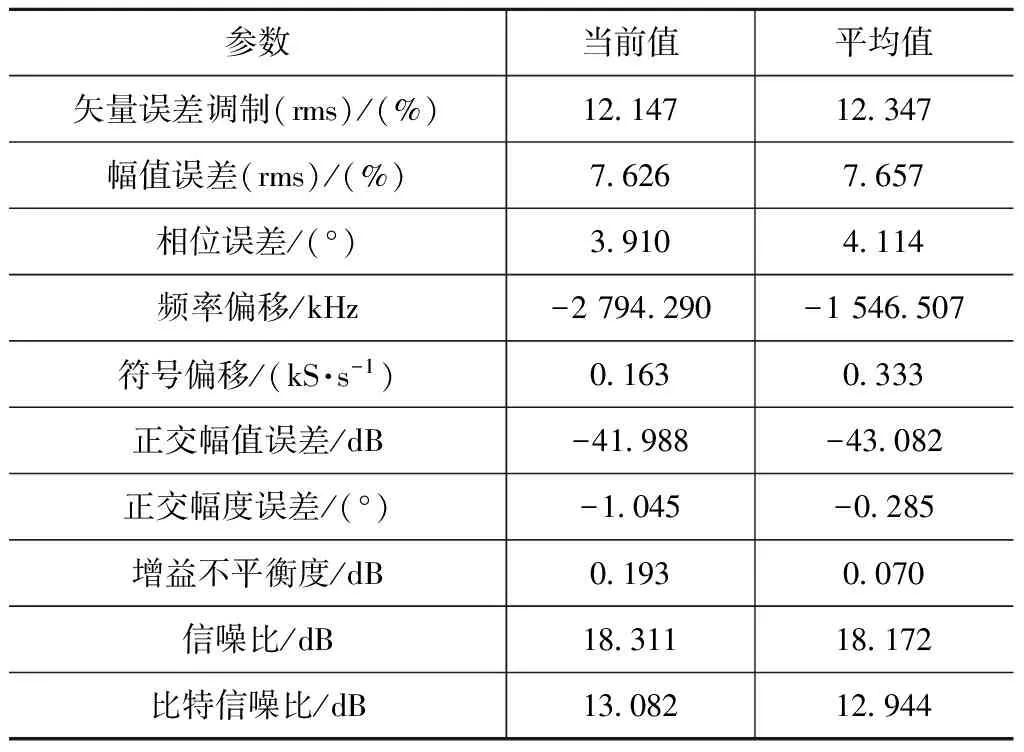
表1 未加預失真系統性能

由圖11、13可知：加本文的改進型預失真算法后，星座圖獲得了明顯改善，且三階帶寬內的頻譜起伏被較好地控制。

由表1、2可知：數據傳輸速率2 Gb/s的寬帶16QAM信號解調的矢量誤差調制(EVM)提高了5.87%(由12.15%提高至6.28%)，信噪比提升5.72 dB(由18.31 dB提高至24.03 dB)；帶外頻譜在未加預失真前，3階交調造成的帶外抑制為18 dB，加預失真程序后帶外抑制為30 dB，提高13 dB。

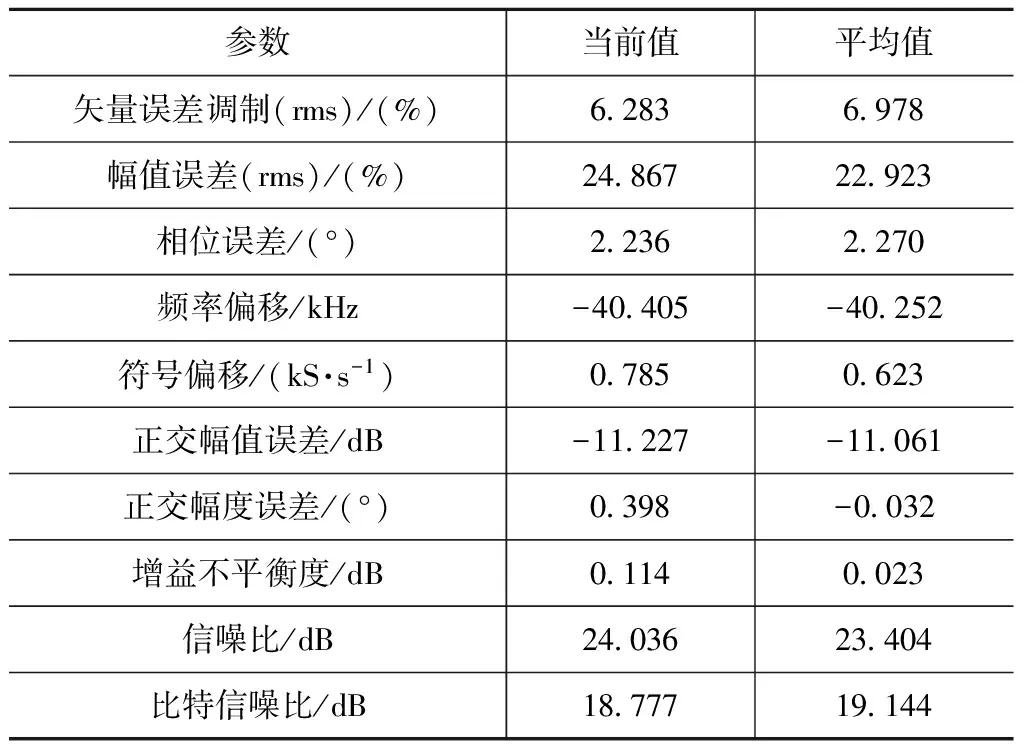
表2 加改進算法后預失真系統性能

綜上，應用本文改進型預失真算法，調制信號帶寬內的信號幅值、相位失真得到了校正，EVM和信噪比指標大幅提高，同時帶寬外的頻譜抑制也得到了明顯改善，整體提升了數傳系統的性能。

4 結束語

本文對星載行波管等功放器件的高速、高帶寬的數字基帶預失真技術進行了研究。提出了一種合理可行的星載數傳應用鏈路補償方案，可方便靈活地進行星載數傳的預失真測試和參數提取；采用并改進了收斂迭代算法，加快了收斂速度，并降低了收斂后的誤差波動，提升了預失真補償性能；搭建了預失真測試系統平臺，并對單通道數據傳輸速率最高達2 Gb/s的16QAM寬帶調制信號的非線性補償效果進行實測，驗證了算法的性能，獲得了較好的非線性補償糾正效果。本文研究提出的改進預失真方案有效解決了衛星高速數據傳輸系統中的射頻通道非線性失真問題，提升了數傳系統的整體性能，可普遍用于功放的非線性失真補償，非線性模型和補償算法與功放具體特性無關。研究為未來星載高階調制方式奠定了基礎。后續，還需研究發送端功能更強大的聯合預失真算法，設想可建立數學模型，通過設置少量參數就能生成一個全新的記憶性聯合預失真特性曲線，通過產生的特性曲線形成濾波系數查找表進行并行高速流水線相加運算，這樣就可用少量的遙控參數產生任意的聯合預失真效果，避免了原先查找表系數固定，聯合預失真系數不能改變的問題，以此形成星上數傳長壽命產品強大的預失真補償功能，提高失真補償的智能性和對射頻通道及傳輸信道的自適應性。

[1] 魏致坤， 強龍凱， 劉波， 等. 高速OQPSK調制技術的濾波器選擇[J].上海航天， 2014， 31(4)： 54-58.

[2] 胡俊杰. 衛星數據傳輸高速調制器關鍵技術研究[D]. 北京： 中國科學院空間科學與應用研究中心, 2011.

[3] 侶秀杰. 記憶功率放大器數字預失真技術研究[D]. 大連: 大連理工大學, 2012.

[4] 董明洋. 寬帶高速數字預失真實現技術研究[D]. 北京: 北京郵電大學, 2012.

[5] ALADR’ EN L, GARCIA P, LUIS CARRO P. Digital predistortion based on zernike polynomial functions for rf nonlinear power amplifiers[J]. ISWCS, 2012： 865-869.

[6] WOO Y Y, KIM J, YI J, et al. Adaptive digital feedback predistortion technique for linearizing power amplifiers, microwave theory and techniques[J]. IEEE Transactions, 2007, 55(5): 932-940.

[7] ALADR’ E N L, GARCIA P, CARRO P L. Digital predistortion based on Zernike polynomial functions for RF nonlinear power amplifiers[J]. ISWCS, 2012: 865-869.

[8] 鄭斌. WCDMA直放站系統中數字預失真技術的設計與實現[D]. 北京: 北京郵電大學, 2010.

[9] PROAKIS J G, MANOLAKIS D G. Digital signal processing principles, algorithms, and applications[M]. 4thEdition. 北京: 電子工業出版社, 2012: 665-682.

[10] PROAKIS J G. Digital communications[M]. 4thEdition. 北京: 電子工業出版社, 2007: 477-507.

[11] 胡欣, 王剛, 王自成. 查找表聯合記憶效應補償技術的寬帶自適應預失真算法[J]. 電子與信息學報, 2012, 34(3): 733-738.

Predistortion Linearizer for RF Power Amplifiers in Spaceborne High-Speed Modulator

XIANG Qian, LI Hui-yuan, YANG Jin-pu

(Shanghai Aerospace Electronic Technology Institute, Shanghai 201109, China)

In order to make up the influence of RF nonlinear power amplifiers in high-speed data transmission system, the digital baseband pre-distortion algorithm was studied and improved in this paper. The LMS and RLS algorithms were analyzed by Matlab simulation. A new method of variable step in iterative convergence algorithm was proposed. The modulated intermediate frequency signal was sampled directly at receving end. The wideband phase-locked loop and relative peak were applied to realize the information synchronism of receiving and transmitting without transmitting data sampling. The linear and nonlinear distortions in the whole channel were compensted. The simulation showed that it would improve the performance and convergence speed. The test results of the 16QAM wide-band signal in a spaceborne high-speed modulator and TWTA system showed that the performance of system with the modified predistortion would be improved, and the influence of RF power amplifiers in high-speed data transmission system was reduced.

Spaceborne high-speed data transmission; Wide-band digital pre-distortion; Nonlinear distortion; Modulator; Linearizer; Variable step in iterative covergence

1006-1630(2016)04-0088-07

2015-09-02；

2015-10-17

總裝備部高分辨率對地觀測系統重大專項(GFZX04013204)

向 前(1980—)，男，高級工程師，主要研究方向為高速調制與解調。

TN914

A

10.19328/j.cnki.1006-1630.2016.04.015