剩余可采儲量采油速度與Arps遞減規律關系
朱圣舉,張皎生,安小平
(1.中國石油長慶油田分公司,陜西 西安 710018;2.低滲透油氣田勘探開發國家工程實驗室,陜西 西安 710018)
?
剩余可采儲量采油速度與Arps遞減規律關系
朱圣舉1,2,張皎生1,2,安小平1,2
(1.中國石油長慶油田分公司,陜西 西安 710018;2.低滲透油氣田勘探開發國家工程實驗室,陜西 西安 710018)
針對鄂爾多斯盆地巖性油藏剩余可采儲量采油速度變化規律難以評價的問題,從定義剩余可采儲量采油速度入手,結合Arps遞減方程,推導出不同遞減規律條件下的剩余可采儲量采油速度方程,并以鄂爾多斯盆地具體油藏為實例進行分析。結果表明:在指數型遞減規律下,剩余可采儲量采油速度等于初始遞減率,為常數;在雙曲線型遞減規律下,剩余可采儲量采油速度隨時間的增大而呈“凹”型下降曲線,與遞減率呈正線性相關,其斜率為1-n(n為遞減指數);在調和型遞減規律下,剩余可采儲量采油速度隨時間呈“凹”型變化規律,且存在極小值,與遞減率呈“凹”型相關,即當時間小于某一點(駐點)時,剩余可采儲量采油速度隨時間的增大(或遞減率的降低)而呈“凹”型降低;當時間大于某一點(駐點)時,剩余可采儲量采油速度隨時間的增大(或遞減率的降低)而呈“凹”型升高。研究成果在巖性油藏以及其他開發規律類似的油藏均可推廣應用。
巖性油藏;剩余儲量;可采儲量;采油速度;產量;Arps遞減;鄂爾多斯盆地
0 引 言
采油速度是評價油藏是否高效合理開發的重要指標,主要包括地質儲量采油速度、可采儲量采油速度及剩余可采儲量采油速度3種[1]。以往在水驅油藏開發效果的評價研究中,有的僅研究了地質儲量采油速度和可采儲量采油速度指標,這些指標中的地質儲量和可采儲量基本是定值,而實際開發過程中的剩余可采儲量在不斷變化[2-3];有的雖然研究了剩余可采儲量采油速度,但并未深入研究其變化規律,且研究不全面[4-7]。
產量遞減規律的研究已經比較成熟,自從Arps提出指數型遞減、雙曲線型遞減及調和型遞減規律以來[8-9],有的學者對這3種遞減規律的滲流理論基礎進行進一步研究[10-14],有的學者對其應用方法進行了研究[15-18]。
鑒于此,從定義剩余可采儲量采油速度入手,結合3種主要遞減方程,推導出了不同遞減規律條件下的剩余可采儲量采油速度方程,并對其變化規律進行了系統的研究,為更加科學地評價油藏開發效果提供了一條新的途徑。
1 3種典型遞減規律的剩余可采儲量采油速度變化規律
1.1 指數型遞減條件
指數型遞減產量公式[13]:
Qt=Qie-Dit
(1)
式中:Qt為原油年產量,t/a;Di為油藏產油量初始遞減率,a-1;t為油藏進入遞減開發期后的時間,a;Qi為產量遞減期t=0時對應的初始產量,t。
指數型遞減累計產量公式[13]:
(2)
式中:Np1為遞減階段原油累計產量,t。
當t→∞時,可得指數型遞減階段可采儲量公式:
(3)
式中:NR1為油藏遞減階段可采儲量,t。
指數型遞減公式[13]:
D=Di
(4)
式中:D為油藏產油量遞減率,a-1。
式(4)表示指數型的遞減率始終保持不變,為Di。則油藏開發全過程可采儲量為:
(5)
式中:NR為油藏開發全過程可采儲量,t;Np0為t=0時的油藏累計產量,t。
為了研究問題的方便,定義遞減階段剩余可采儲量采油速度為:
(6)
將式(1)~(4)代入式(6),得:
υor=Di=D
(7)
式(7)說明,在指數型遞減條件下,剩余可采儲量采油速度保持不變,等于初始遞減率。
1.2 雙曲線型遞減條件
雙曲線型遞減產量公式[13]:
Qt=Qi(1+nDit)-1/n
(8)
式中:n為遞減指數(0 雙曲線型遞減累計產量公式[13]: (9) 當t→∞時,可得雙曲線型遞減階段可采儲量公式: (10) 雙曲線型遞減公式[13]: (11) 式(11)表示雙曲線型的遞減率隨著時間的增大而減小。 則油藏開發全過程可采儲量為: (12) 將式(8)~(10)代入式(6),得: (13) 將式(11)代入式(13),得: υor=(1-n)D (14) 由式(14)可知:在雙曲線型遞減條件下,剩余可采儲量采油速度與遞減率呈正線性相關,其斜率為1-n。 式(13)兩邊同時對時間t求導數: (15) 式(15)兩邊再同時對時間t求導數: (16) 式中:υ″or為υor對t的二階導數。 1.3 調和型遞減條件 調和型遞減產量公式[13]: (17) 調和型遞減累計產量公式[13]: (18) 調和型遞減公式[13]: (19) 式(19)表示調和型的遞減率隨著時間的增大而減小。 將式(17)、(18)代入式(6),得: (20) 將式(19)代入式(20),得: (21) 式(20)兩邊同時對時間t求導數: (22) X隨著t的增大而減小。則式(22)可變為: (23) 式(23)兩邊同時對時間t求導數: (24) (25) 式中:tb為駐點,a。 將式(25)代入式(24),得: (26) 在t=tb點,剩余可采儲量采油速度υor存在極小值,即當開發時間達到某一點(駐點)時,剩余可采儲量采油速度達到極小值。 又由式(19)可知,調和遞減的遞減率是隨著開發時間的增大而逐漸減小的,所以在調和遞減條件下,剩余可采儲量采油速度與遞減率呈“凹”型相關,即當時間小于某一點(駐點)時,剩余可采儲量采油速度隨遞減率的降低而降低;當時間大于某一點(駐點)時,剩余可采儲量采油速度隨遞減率的降低而升高。 由上述分析可知,指數型遞減規律中,剩余可采儲量采油速度等于初始遞減率,是不變的。所以,只列舉分析雙曲線型和調和型遞減規律中的剩余可采儲量采油速度變化規律。 實際應用中,先由式(1)、(8)、(17)對實際數據進行擬合,確定具體符合哪一種遞減規律。如果符合指數遞減規律,則可由式(7)求出υor;如果符合雙曲線遞減規律,則可由式(13)求出υor—t的變化規律,由式(14)求出υor—D的變化規律;如果符合調和遞減規律,則可由式(20)求出υor—t的變化規律,由式(21)求出υor—D的變化規律。 鄂爾多斯盆地X砂巖油藏,油層有效厚度為9.2m,空氣滲透率為254×10-3μm2,孔隙度為17%,原始含油飽和度為0.60,地層原油黏度為5.23mPa·s,原始溶解氣油比為13.3m3/t,注水開發,遞減規律符合雙曲線遞減規律,其剩余可采儲量采油速度(υor)隨時間(t)的增大呈逐漸遞減趨勢(圖1),實際值與理論計算值相對誤差為1.2%;剩余可采儲量采油速度與遞減率呈正線性相關,實際值與理論計算值相對誤差為2.1%(圖2)。 圖1 不同遞減規律下υor隨t變化規律 圖2 不同遞減規律下υor隨D變化規律 鄂爾多斯盆地H砂巖油藏,油層有效厚度為9.5m,空氣滲透率為3.49×10-3μm2,孔隙度為15%,原始含油飽和度為0.64,地層原油黏度為1.15mPa·s,原始溶解氣油比為103.6m3/t,注水開發,遞減規律符合調和遞減規律,剩余可采儲量采油速度隨時間的增大呈先下降后上升的趨勢,實際值與理論計算值相對誤差為3.4%。在某一點處(tb=20.48a),剩余可采儲量采油速度有極小值(0.033 9)(圖1);剩余可采儲量采油速度與遞減率呈“凹”型相關,實際值與理論計算值相對誤差為3.6%(圖2)。 由于剩余可采儲量采油速度是主動可調的,而遞減率是被動產生的,因此,在油藏開發過程中,剩余可采儲量采油速度的調整應遵循具體油藏的實際開發規律。X油藏和H油藏的剩余可采儲量采油速度始終在趨勢線附近,其遞減規律也按趨勢線運行,保持了較好的開發效果。X油藏的地質儲量采出程度已達到27%,預計采收率可達到35%;H油藏的地質儲量采出程度已達到12%,預計采收率可達到25%。 (1) 在指數型遞減規律下,剩余可采儲量采油速度等于常數(即初始遞減率)。 (2) 當油藏產量呈雙曲線型遞減規律時,剩余可采儲量采油速度隨時間的增大呈“凹”型下降曲線;當油藏產量呈調和型遞減規律時,剩余可采儲量采油速度隨時間的增大呈先“凹”型下降后“凹”型上升的變化規律,在某一點處,剩余可采儲量采油速度存在極小值。 (3) 當油藏產量呈雙曲線遞減規律時,剩余可采儲量采油速度與遞減率呈正線性相關。 (4) 當油藏產量呈調和型遞減規律時,剩余可采儲量采油速度與遞減率呈“凹”型相關。當開發時間小于某一點(駐點)時,剩余可采儲量采油速度隨遞減率的降低而降低;當開發時間大于某一點(駐點)時,剩余可采儲量采油速度隨遞減率的降低而升高。 [1] 王玉普,劉義坤,鄧慶軍.中國陸相砂巖油田特高含水期開發現狀及對策[J].東北石油大學學報,2014,38(1):1-9. [2] 蔣有偉.遼河油區注水開發油田產液量變化規律認識[J].特種油氣藏,2005,12(4):58-59. [3] 王學忠.應用可采儲量采油速度法劃分多層砂巖油藏開發階段[J].特種油氣藏,2004,11(6):50-51. [4] 孫娜.低滲透油藏水驅開發效果綜合評價方法研究與應用[J].特種油氣藏,2008,15(6):56-58. [5] 張崇剛.模糊層次評價法在海南3斷塊的應用[J].特種油氣藏,2009,16(6):52-54. [6] 王敏,陳民鋒,劉廣為,等.主成分分析法確定海上油田水驅效果評價關鍵指標[J].油氣地質與采收率,2015,22(2):112-116. [7] 俞啟泰,李文興.一種新的預測油田產量變化的方法——剩余可采儲量采油速度法[J].石油勘探與開發,1997,24(6):82-85. [8]ARPSJJ.Analysisofdeclinecurve[J].Trans.A.I.M.E,1945(160):228-247.[9]ARPSJJ.Estimationofprimaryoilreserves[J].Trans.A.I.M.E,1956(207):182-186.[10] 計秉玉.產量遞減方程的滲流理論基礎[J].石油學報,1995,16(3):86-91. [11] 白玉湖,王小林,陳桂華,等.流動階段頁巖油氣典型曲線分段預測方法[J].特種油氣藏,2014,21(6):112-114. [12] 孔憲政.薩南開發區水驅遞減率預測[J]. 大慶石油地質與開發,2014,33 (4):84-86. [13] 黃炳光,劉蜀知.實用油藏工程與動態分析方法[M].北京:石油工業出版社,1998:174-176. [14] 顧喬元,張繼風,張大鵬,等.D油田東河砂巖組產量遞減規律[J].大慶石油地質與開發,2014,33(1):62-65. [15] 劉雄志,楊兆平,惠學智,等.小孔剩余油受力分析及數學模型的改進[J].大慶石油地質與開發,2014,33(2):77-82. [16] 侯健,羅福全,李振泉,等.巖心微觀與油藏宏觀剩余油臨界描述尺度研究[J].油氣地質與采收率,2014,21(6):95-98. [17] 裴連君,王仲林.Arps遞減曲線與甲型水驅曲線的相關性及參數計算[J].石油勘探與開發,1996,26(3):62-65. [18] 孔憲政.薩南開發區水驅遞減率預測[J].大慶石油地質與開發,2014,33(4):84-86. 編輯 張耀星 20151227;改回日期:20160301 國家科技重大專項“鄂爾多斯盆地大型低滲透巖性地層油氣藏開發示范工程”(2011ZX05044) 朱圣舉(1963-),男,高級工程師,1984年畢業于江漢石油學院采油工程專業,1996年畢業于該校油氣田開發工程專業,獲碩士學位,現主要從事油藏工程研究、低滲透油田開發、提高采收率等相關研究工作。 10.3969/j.issn.1006-6535.2016.04.024 TE A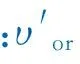
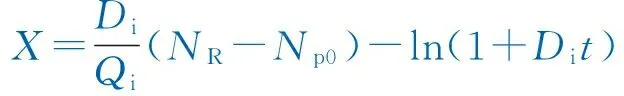
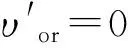
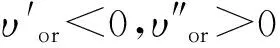
2 實例分析
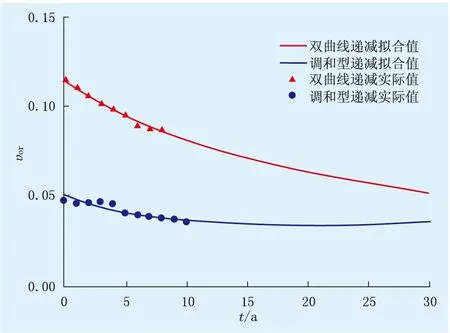
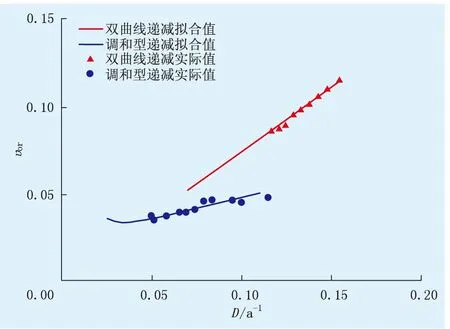
3 結 論

