攜能通信協作認知網絡穩態吞吐量分析和優化

闊永紅，賀冰濤，陳 健

(西安電子科技大學 通信工程學院，陜西 西安 710071)

?

攜能通信協作認知網絡穩態吞吐量分析和優化

闊永紅，賀冰濤，陳 健

(西安電子科技大學 通信工程學院，陜西 西安 710071)

在攜能通信協作認知網絡中，針對主用戶和認知用戶的非飽和數據傳輸問題，研究主用戶網絡和認知用戶網絡穩態吞吐量之間的相互作用關系，并對認知網絡進行穩態吞吐量的優化．首先，提出一種“概率協作”的傳輸策略，采用排隊論的方法對該場景進行網絡層建模和分析，求解出系統的穩態吞吐量域，并以此反映主用戶網絡和認知用戶網絡的相互作用關系．其次，通過求解“概率協作”策略中認知用戶的最優協作傳輸概率，在保證主用戶系統穩定的情況下，最大化認知用戶的穩態吞吐量．仿真結果和分析表明，采用“概率協作”的傳輸策略能使認知用戶獲得最大的穩態吞吐量，同時，主用戶網絡相比于無協作時的系統性能也有了較大的提升．

攜能通信;認知無線電;協作通信;穩態吞吐量

協作認知無線電網絡(Cooperative Cognitive Radio Network， CCRN)中認知節點通過對授權節點協作與授權網絡共享頻段，是一種高頻譜利用率的雙贏通信技術[1-2]．然而，在現實中充當協作中繼的認知用戶并不是充足供能的基站，而是一些低功耗的節點[3]，這些節點由于僅裝載儲能有限的電池進行通信，很大程度上制約了網絡的生存時間[4]．基于攜能通信的協作認知網絡[3]在傳統的CCRN中采用無線攜能通信技術(Simultaneous Wireless Information and Power Transfer， SWIPT)，可使認知用戶在感知和接收主用戶射頻信號的同時，通過能量回收技術(Energy Harvesting， EH)從承載信息的無線電射頻信號中獲得傳輸能量，實現能量與信息的并行傳輸，可有效解決CCRN中節點能量受限的問題，延長節點生存時間，為進一步提升譜效和能效提供了有效的手段．

在采用攜能通信技術的CCRN中已有大量文獻[3，5-6]采用香農容量來表征系統的最大可達速率，并以此來衡量和分析系統性能．在實際的數據傳輸中主用戶和認知用戶并非時刻都有數據需要傳輸，即數據包的產生時刻和傳輸持續的時間具有不確定性，這使得用戶緩存器中的數據包隊列是非飽和的，而采用香農容量并不能描述在該情況下系統的長程性能(隊列的穩定性及時延等[7])．針對數據的非飽和傳輸問題，文獻[8]在基于攜能通信認知網絡中采用排隊論的方法進行了網絡層的系統性能優化，在保證主用戶系統穩定的同時，通過優化認知網絡的傳輸概率使認知網絡的穩態吞吐量最大化．然而，該研究并未涉及主用戶與認知用戶間的相互協作．針對協作通信中非飽和數據傳輸問題的研究，文獻[9]在三節點的攜能通信協作中繼網絡中，分析了中繼節點能量收集與數據包協作傳輸間的切換對系統性能的影響．文獻[2，10]在傳統的CCRN中分別對單認知用戶節點和多認知用戶節點的協作場景，通過穩態吞吐量域直觀反映了該多接入網絡中，主用戶穩態吞吐量和認知用戶穩態吞吐量之間的相互作用關系．在采用攜能通信的CCRN中，認知用戶的穩態吞吐量不僅會受到主用戶業務傳輸強度的影響，同時也會受到自身傳輸能量的制約．一方面，隨著主用戶傳輸的頻繁，認知用戶可以更多地從主用戶傳輸的信號中獲得傳輸能量用于自身的數據傳輸，但主用戶頻繁占用信道使得認知用戶的傳輸機會減少; 另一方面，由于認知用戶對主用戶的協作增大了認知用戶的傳輸機會，但同時認知網絡又要消耗部分的能量進行協作傳輸．因此，在非飽和通信情況下，對攜能通信的CCRN的穩態吞吐量的分析，需要聯合考慮主用戶活動、認知用戶能量狀態及認知用戶的傳輸機會．

綜上所述，針對攜能通信的協作認知網絡中的非飽和數據通信問題，筆者分析主用戶網絡和認知用戶網絡穩態吞吐量之間的相互作用關系，并最大化認知網絡系統的穩態吞吐量，使認知網絡能夠承載較高的數據包到達率．首先，在該場景中提出一種部分協作策略[11]，即對主用戶進行概率性的協作，并采用排隊論求解出該系統的穩態吞吐量域，來反映主用戶網絡和認知用戶網絡穩態吞吐量之間的相互作用關系; 其次，在保證主用戶網絡隊列穩定的前提下，通過求解最優協作概率c，使認知網絡的穩態吞吐量最大化; 最后，通過仿真分析了在不同協作策略下系統的穩態吞吐量域，及不同能量轉化效率對系統性能的影響．

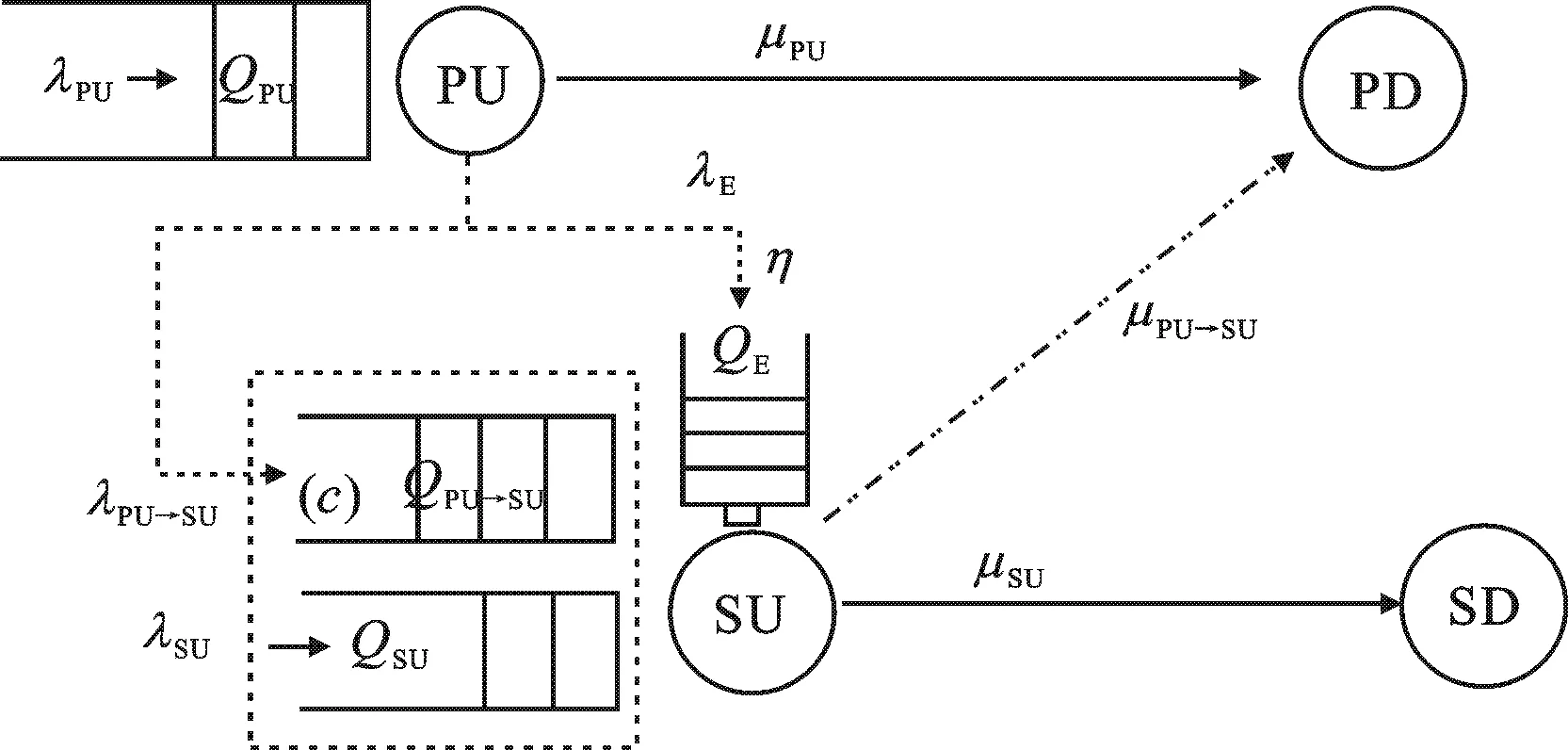
圖1 系統模型

1 系統模型

在圖1所示的系統中，由主用戶基站PU、主用戶接收端PD和認知用戶節點SU、認知用戶接收端SD構成．圖中PU有1個無限長緩存器QPU，用來存儲主用戶隨機到達的等長數據包．SU有2個無限長緩存器，QPU→SU用來存儲主用戶目的端PD未成功接收而SU成功接收的主用戶數據包;QSU用來儲存認知用戶隨機到達的等長數據包．QPU、QSU中數據包的到達過程均為伯努利過程．PU為能量非受限節點，SU僅通過射頻能量回收技術從PU發送的射頻信號中獲取能量，并儲存在無限長的能量儲存裝置QE中，其能量的轉化效率為η[8]．

主用戶和認知用戶的信道接入方式設定如下[8，10]:

(1) 當主用戶有數據傳輸時(緩存器QPU的數據包隊列非空)會占用授權信道進行傳輸，認知用戶只能在未被主用戶占用的時段內進行數據傳輸．

(2) 主用戶或認知用戶的目的端成功接收到各自用戶發送的信息后，會通過完美的反饋信道來廣播ACK應答消息; 若未成功接收，則廣播NACK，且在下一個時隙內進行數據包的重傳．

(3) 對主用戶目的端未成功接收到的數據包，若該數據包能成功被認知用戶接收，認知用戶可選擇不協作而直接將該數據包丟棄，此時主用戶需進行重傳．也可選擇協作主用戶重傳，將該數據包儲存在協作緩存器QPU→SU，并等待空閑時刻傳出，此時主用戶會將該傳輸失敗的數據包從隊列中移除不重傳該數據包．

(4) 認知用戶的傳輸包含兩個緩存器的傳輸(QPU→SU、QSU)，當認知用戶獲得空閑時間進行數據傳輸時，要優先傳輸儲存在節點中主用戶的數據，即只有當協作緩存器QPU→SU中沒有數據包時才可傳輸自己的數據包．同時認知用戶能量受限，因此，只有當能量儲存裝置QE非空時，才能進行數據傳輸．

(5)pPU→PD、pPU→SU、pSU→PD、pSU→SD分別表示主用戶PU數據包成功被目的端PD接收的概率、主用戶PU數據包成功被認知用戶SU接收的概率、儲存在QPU→SU中的數據包成功被主用戶目的端PD接收的概率、認知用戶自身數據包成功被認知用戶目的端SD接收的概率．

筆者將一個等長數據包傳輸的時間作為一個時隙，且一個數據包傳輸所消耗的能量為一個單元塊，相比于傳輸所消耗的能量，可忽略感知和信號處理所消耗的能量[12]．

2 穩態吞吐量的建模和分析

本節對攜能通信的協作認知網絡的系統穩定性進行分析，并求出系統的穩態吞吐量域．由Loynes定理可得系統能夠處于穩定狀態的條件:

其中，λPU、λPU→SU和λSU分別為主用戶數據包的到達率、協作數據包的到達率和認知用戶數據包的到達率；μPU、μPU→SU和μSU分別為主用戶數據包的服務率、協作數據包的服務率和認知用戶數據包的服務率．主用戶和認知用戶的最大穩態吞吐量可定義為滿足系統穩定性條件下，主用戶節點和認知用戶節點所分別能承載的數據包的最大到達強度，即λPU及λSU的上界．系統的吞吐量域為所有滿足系統穩定條件的服務率對(λPU， λSU)所組成的集合．下面針對主用戶網絡和認知用戶網絡分別求出μPU和μSU及系統的吞吐量域．

2.1 主用戶網絡

在該協作場景中，主用戶網絡的平均服務率μPU可表示為

當PU發送的數據包未能被PD成功解碼而被SU成功解碼后，SU可以概率c選擇協助主用戶傳輸該數據包．c ∈ [0，1]，當c取0時，表示認知用戶不協助主用戶；當c取1時，表示認知用戶完全對主用戶進行協作．認知用戶通過協作可盡快清空主用戶隊列為認知用戶創造更多傳輸機會，但由于節點的能量受限，使得一部分空閑時間并不能被用來傳輸認知用戶的數據．因此，在下一節會對c進行優化，使認知用戶的傳輸能量和傳輸機會達到最優折中．

主用戶的數據包的到達率為λPU，則主用戶占用信道的概率UPU可以表示為主用戶隊列QPU非空的概率，由Little定理可得

2.2 認知用戶網絡

認知用戶網絡的平均服務率μSU可表示為

其中，Pr[QPU=0]=1-UPU．為求得認知用戶協作緩存器中隊列為空的概率Pr[QPU→SU=0]，應求出協作緩存器中數據包的到達率λPU→SU及服務率μPU→SU．

其中，ψ表示數據包未成功被PD接收，但成功被SU接收事件；Pr[QE≠ 0]為認知用戶能量隊列非空概率，即認知用戶有能量進行傳輸的概率．由于認知用戶是通過主用戶發射的信號獲取能量，在一個時隙內可接收到單位能量的概率為UPU．認知用戶的能量到達率 λE= UPUη，η為能量轉化效率，認知用戶能量隊列非空的概率Pr[QE≠ 0]可由文獻[13]得到:

綜上可得，認知用戶網絡的平均服務率μSU為

2.3 系統穩態吞吐量域

由系統的穩定條件可得系統的穩態吞吐量域為

其中，Δ=c pPU→SU(1-pPU→PD)．在該系統中主用戶網絡所能達到的最大穩態吞吐量受協作概率c的影響，認知用戶可達到的最大穩態吞吐量由主用戶的業務傳輸強度(數據包到達率λPU)、協作概率c和能量轉化率η共同決定．對于固定能量轉化率的認知用戶為使其能達到最優的性能，需要根據主用戶的傳輸行為來自適應地調整自己的協作策略，從而最大化自身的穩態吞吐量．

3 協作概率優化

由上述分析，下面在保證主用戶隊列穩定的前提下，通過優化協作概率c，最大化認知網絡的穩態吞吐量，即

將式(10)寫為有關λPU和λSU的表達式為

分別將F(1)、F(2)對c求導，有

通過求導可知，F(1)為單調遞減函數，F(2)的增減性只取決于pPU→PD和pSU→PD的關系．下面針對 pPU→PD> pSU→PD和 pPU→PD≤ pSU→PD兩種情況分別對最優的協作概率c進行求解．

(1) pPU→PD>pSU→PD: 主用戶自身傳輸成功的概率高于認知用戶協助傳輸成功的概率，此時λPU的取值范圍為(0，pPU→PD)．F(1)、F(2)均為單調遞減函數，在該條件下最大化問題即為根據約束條件求c的下界．將約束條件式(11b)、(11c)和式(11d)寫為如下形式:

對于任意的λPU∈(0，pPU→PD)，由式(14a)與式(14d)可求得c的下界為負數，又 c ∈ [0，1]，最優的協作概率c均為其下界取值0．這表明當主用戶自身傳輸成功的概率高于認知用戶協助傳輸成功的概率時，為使認知用戶穩態吞吐量最大化，認知用戶不應當對主用戶進行協作．這是因為，雖然認知用戶對主用戶協作能盡快清空主用戶的數據包使認知用戶獲得更多的頻譜接入時間，但在空閑的時間內認知用戶要優先傳輸主用戶未能成功傳輸的數據包，而認知用戶協作主用戶重傳所耗費的時間卻高于主用戶自身重傳所耗費的時間，這樣一方面使得認知用戶傳輸自己數據包的機會減小，另一方面，使認知用戶只能用更少的能量來傳輸自身數據包．

(2) pPU→PD≤pSU→PD: 即認知用戶協助傳輸成功的概率高于主用戶自身傳輸成功的概率，此時λPU的取值范圍為(0，pSU→PD)．F(1)為單調遞減函數，F(2)為單調非減函數，μSU的最大值可在F(1)和F(2)的交點處取得．令 F(1)= F(2)，可求得交點處對應的協作概率c，記作cst1．

在該條件下μSU的最大化問題，需根據約束條件求c的取值范圍并判斷cst1與c的取值范圍的關系來求解最優的協作概率c．將約束條件式(11d)化簡，可得

不等式(16)左右兩邊的正負性會受到λPU取值的影響從而使c的取值范圍發生變化，下面將在λPU不同的取值區間分別對最優的協作概率c進行求解．

(1) 當pSU→PD> λPU>pPU→PD時，可將約束條件式(11b)、(11c)和式(11d)寫為如下形式:

為保證系統穩定，應有cst3> cst2，cst3> cst4，由此可得

可由約束條件求得c的上界為min(cst3，1)，c的下界為max(0，cst2，cst4)．當交點cst1大于c的上界時，最優的c應取上界; 當交點cst1處于c取值范圍內時，最優的c應取交點cst1; 當交點cst1小于c的下界時，最優的c應取下界．在該條件下的最優協作概率c可表示為

(2) 當pPU→PD≥λPU時，可將約束條件式(11b)、(11c)和式(11d)簡化為如下形式:

同理可得，在該條件下的最優協作概率c為

認知用戶的最優協作概率受主用戶的傳輸和能量轉化率的聯合約束，下面結合仿真結果做具體分析．

4 仿真結果與分析

從上面的分析中可知，在pPU→PD>pSU→PD時，認知用戶最優的協作概率恒為0．為研究協作對系統性能的影響，下面將對主用戶傳輸成功概率低于認知用戶協助傳輸成功概率 (pPU→PD≤ pSU→PD)的情況進行仿真．不同傳輸路徑下數據包成功傳輸的概率假設如下: pPU→PD= 0.5，pPU→SU= 0.8，pSU→PD= 0.9，pSU→SD= 0.8[2]．

圖2給出了在能量轉化率η=0.8時，不同協作策略下系統穩態吞吐量域．圖3給出了在能量轉化率 η=0.8 時，不同協作策略下主用戶未占用信道的概率和認知用戶能量非空的概率曲線．從圖2中可看出，采用最優協作概率的“概率協作傳輸”策略相比于無協作傳輸和完全協作傳輸策略有更大的穩態吞吐量域．

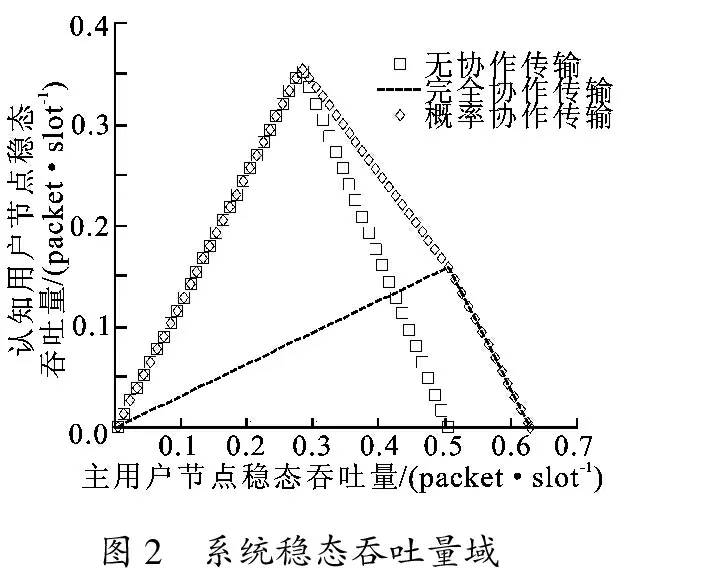
圖2 系統穩態吞吐量域

圖3 信道占用狀態與能量狀態

結合圖2和圖3進行分析，當λPU≤0.28(式(22)中cst1≤0)時，“概率協作傳輸”策略的最優協作概率為0，即“無協作傳輸”．由圖3可知，此時認知用戶雖有大量傳輸機會，但認知用戶可獲得的射頻能量較少導致系統穩態吞吐量較低．當λPU由0.00增大到0.28時，認知用戶損失了部分傳輸機會，卻獲得更多能量用于自身數據包傳輸，使認知用戶的吞吐量逐漸上升．當λPU繼續增大時，認知用戶可獲得的傳輸能量逐漸趨于飽和態，即能量隊列中總有剩余能量，但主用戶更多地占用信道卻使認知用戶的傳輸機會大幅減少．“概率協作傳輸”策略將以一定的概率協作主用戶清空主用戶隊列，“完全協作傳輸”策略相比于“概率協作傳輸”策略可使認知用戶獲得更多傳輸機會，但一方面使認知用戶從主用戶信號中獲得總能量的頻率減少，另一方面卻需消耗更多能量進行協作傳輸．“概率協作傳輸”策略通過動態調整認知用戶的協作概率，將認知用戶的傳輸能量和傳輸機會很好地折中．當 λPU≥ 0.5時，認知用戶最優協作概率為1，即“完全協作傳輸”．

圖4給出了不同能量轉化率下認知用戶的最優協作概率取值．圖中λPU的取值受到式(11)的約束，因此，在不同能量轉化率下的可取的最大值不同．當能量轉化率較低 (η= 0.1，η= 0.4)時，認知用戶的最大協作概率均不能達到1，即不能采用“完全協作傳輸”策略，這是由于在較低的能量轉化率下認知用戶獲得的能量較少，認知用戶只能對主用戶傳輸失敗的部分數據包進行協作．若對主用戶傳輸失敗的所有數據包都進行協作，則會使認知用戶的服務率小于數據包的到達率，不能滿足QPU→SU隊列的穩定條件．從圖中可看出，隨η的增大，c的曲線會在更小的λPU下有數值且以更快的速度增長到1．這是由于在較高的能量轉化率下，認知用戶在較小的λPU便可獲得較為充足的能量， 因此， 可以將一部分能量用來協助主用戶傳輸， 盡快清空主用戶的數據包，使自身獲得更多傳輸機會，并利用協作所獲得的傳輸機會來傳輸自身的數據包．

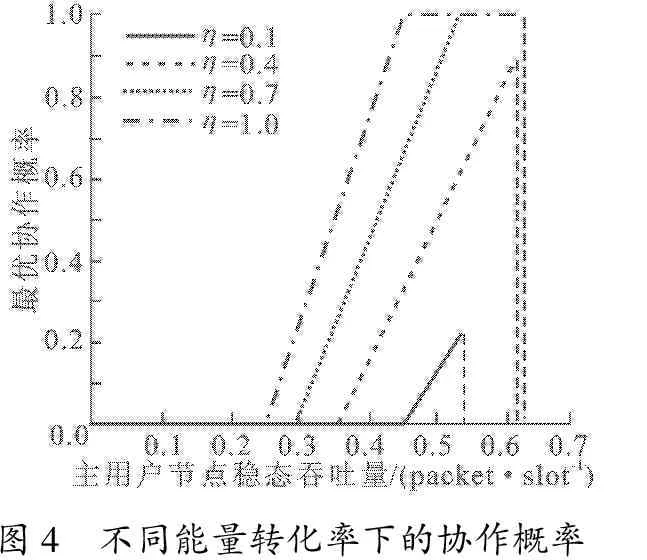
圖4 不同能量轉化率下的協作概率

圖5 不同能量轉化率下的系統穩態吞吐量域

圖5給出了采用概率協作策略時，不同能量轉化率下的系統穩態吞吐量域．能量轉化率越高，系統可獲得的吞吐量域越大．但從圖中可看出，認知用戶的穩態吞吐量增加的幅度越來越小．在較低的能量轉化率下，增大能量轉化率意味著認知用戶有更多的能量來傳輸自己的數據包，但隨著轉化率的不斷增大，傳輸機會的限制使得認知用戶并不能將收集到的全部能量用于自身的數據傳輸．

5 結 束 語

在攜能通信協作認知網絡中考慮更為實際的非飽和通信，對該系統進行網絡層的建模分析．通過求解該系統的穩態吞吐量域直觀反映主用戶和認知用戶吞吐量之間的相互影響．針對認知用戶的傳輸機會和能量之間的折中問題，提出概率協作傳輸策略最大化認知用戶的穩態吞吐量．通過仿真分析，在保證主用戶隊列穩定的前提下，采用“概率協作”傳輸策略的系統的性能優于“無協作傳輸”和“完全協作傳輸”策略; 增大能量轉化效率可提升認知用戶的穩態吞吐量，但這種影響會隨著能量轉化率的增大而減弱．

[1] CAO B, MARK J W, ZHANG Q Y, et al. On Optimal Communication Strategies for Cooperative Cognitive Radio Networking [C]//Proceedings of IEEE International Conference on Computer Communications. Piscataway: IEEE, 2013: 1726-1734.

[2]KOMPELLA S, NGUYEN G D, WIESELTHIER J E, et al. Stable Throughput Tradeoffs in Cognitive Shared Channels with Cooperative Relaying [C]//Proceedings of IEEE International Conference on Computer Communications. Piscataway: IEEE, 2011: 1961-1969.

[3]ZHENG G, HO Z, JORSWIECK E A, et al. Information and Energy Cooperation in Cognitive Radio Networks [J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2290-2303.

[4]LIU L, ZHANG R, CHUA K C. Wireless Information Transfer with Opportunistic Energy Harvesting [J]. IEEE Transactions on Wireless Communications, 2013,12 (1):288-300.

[5]WANG Z H, CHEN Z Y, LUO L, et al. Outage Analysis of Cognitive Relay Networks with Energy Harvesting and Information Transfer [C]//2014 IEEE International Conference on Communications. Piscataway: IEEE Computer Society, 2014: 4348-4353.

[6]KRIKIDIS I, TIMOTHEOU S, NIKOLAOU S, et al. Simultaneous Wireless Information and Power Transfer in Modern Communication Systems [J]. IEEE Communications Magazine, 2014, 52(11): 104-110.

[7]SADEK A K, LIU K J R, EPHREMIDES A. Cognitive Multiple Access via Cooperation: Protocol Design and Performance Analysis [J]. IEEE Transactions on Information Theory, 2007, 53(10): 3677-3696.

[8]LU Y, WANG W, ZHANG Z Y, et al. Random Access for a Cognitive Radio Transmitter with RF Energy Harvesting [C]//2014 IEEE Global Communications Conference. Piscataway: IEEE, 2014: 923-928.

[9]KRIKIDIS I, TIMOTHEOU S, SASAKI S. RF Energy Transfer for Cooperative Networks: Data Relaying or Energy Harvesting? [J]. IEEE Communications Letters, 2012, 16(11): 1772-1775.

[10]FANOUS A, EPHREMIDES A. Stable Throughput in a Cognitive Wireless Network [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(3): 523-533.

[11]PAPPAS N, JEON J, EPHREMIDES A, et al. Wireless Network-level Partial Relay Cooperation [C]//Proceedings of IEEE International Symposium on Information Theory. Piscataway: IEEE, 2012: 1122-1126.

[12]JEON J, EPHREMIDES A. On the Stability of Random Multiple Access with Stochastic Energy Harvesting [J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 571-584.

[13]KASHEF M, EPHREMIDES A. Optimal Partial Relaying for Energy Harvesting Wireless Networks [J]. IEEE/ACM Transactions on Networking, 2016, 24(1): 113-122.

(編輯：李恩科)

Stable-throughput analysis and optimization of cooperative cognitive radio networks based on information and energy cooperation

KUOYonghong，HEBingtao，CHENJian

(School of Telecommunications Engineering, Xidian Univ., Xi’an 710071, China)

According to the unsaturated data traffic in wireless communications, this paper studies the interaction between primary users (PUs) and secondary users (SUs) in a cooperative cognitive radio network which is based on information and energy cooperation, and optimizes the stable-throughput of SUs. A probabilistic cooperation scheme has been proposed and the stable-throughput region has been characterized in order to reflect the interaction between PUs and SUs by using the Queuing Theory. Then by deriving the optimal value of the relaying probability, the stable-throughput of secondary users can be maximized under the constraint of the primary queue stability. Simulation results and theoretical analysis show that the probabilistic cooperation scheme can achieve maximal stable-throughputs for SUs, and meanwhile PUs can also have a better performance compared to the non-cooperative case.

simultaneous wireless information and power transfer;cognitive radio;cooperative communication;stable-throughput

2015-06-27

時間：2016-04-01

國家自然科學基金資助項目(61440056)；高等學校學科創新引智計劃資助項目(B08038)

闊永紅(1967-), 女，教授，博士，E-mail：yhkuo@mail.xidian.edu.cn．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.002.html

10.3969/j.issn.1001-2400.2016.06.001

TN92

A

1001-2400(2016)06-0001-07