西湖凹陷致密低滲砂巖測井解釋模型

李鈞軻，李德勇

（中國海洋大學海洋地球科學學院，山東青島266100）

西湖凹陷致密低滲砂巖測井解釋模型

李鈞軻*，李德勇

（中國海洋大學海洋地球科學學院，山東青島266100）

在巖石結構復雜的低孔滲儲層中，如何根據已有的巖芯、測井等資料來更加精確地求取儲層物性參數是十分重要也十分困難的。不同工區的地質特征、流體性質、儲集特征各不相同，因此也應對不同的測井解釋模型。在借鑒前人研究的基礎上，根據本工區的巖芯、測井資料，利用交會圖和直方圖技術建立了針對本工區的儲層測井解釋模型，提高了本工區低孔滲儲層的測井解釋精度，為后期勘探開發工作提供了嶄新思路和可靠依據。

西湖凹陷；測井解釋模型；孔隙度；滲透率；含水飽和度

西湖凹陷位于東海盆地陸架邊緣，是東海盆地中面積最大、勘探程度最高的沉積凹陷，呈北北東—北東走向，南北長約420km，東西寬約100km，面積約4.27× 104km2。西湖凹陷自老到新發育有古新統、下始新統、中上始新統（平湖組）、漸新統（花港組段）、中新統（龍井組、玉泉組和柳浪組）、上新統（三潭組）及第四系（東海群）。其中，龍井組、花港組、平湖組地層為西湖凹陷勘探的目的層，而花港組是本文研究的重點地層。花港組主要發育于浙東坳陷，厚1000～2000m。

1 概述

儲層測井解釋的主要任務是將自然伽馬、縱橫波聲波時差、電阻率、密度、自然電位等測井曲線依據不同的地質特征選取合適的解釋模型，計算成泥質含量、孔隙度、滲透率、含水飽和度等物性參數。最后，根據這些地質參數，研究儲層及其巖性、物性和含油性，包括儲油性能、滲濾特性、流體性質及產烴能力，以便對地下地質情況、產層特征、油氣層分布與生產能力做出全面評價及符合地下原貌的模擬，從而在宏觀上顯示出較高的精度和較好的經濟效益[1]。為了提高儲層測井解釋模型的計算精度，在針對此工區進行儲層測井解釋模型時，對關鍵井儲層巖芯基本資料進行分析并進行巖芯歸位等處理。對該工區測井資料進行環境校正、深度校正、濾波處理、標準化及歸一化處理，最終建立該工區精確的儲層測井解釋模型。

2 測井解釋模型

2.1 地層泥質含量

地層泥質含量是評價儲層物性及巖性的一個重要參數，是由各種細粉砂、粘土礦物、直徑小于0.01mm的非粘土礦物細顆粒組成的復雜混合物。因此準確計算地層泥質含量是一個必要和復雜的問題[2]。此次工區研究層位為含泥質砂巖，通過對比前人研究成果并結合西湖凹陷地區儲層特征，認為自然伽馬測井能較好地反映地層泥質含量，因此選取自然伽馬測井曲線（GR）計算地層泥質含量（Vsh）。

在實際計算過程中，采取（1）、（2）式計算泥質含量。

式中：GR——自然伽馬測井值，API；

SH——曲線相對值，又稱泥質含量指數，若SH≤0,SH=0.001，若SH≥1,SH=1；

Gmin——純砂巖的自然伽馬測井值，API；

Gmax——純泥頁巖的自然伽馬測井值，API；

GCUR——地層年代系數,第三系以下老地層取2，新地層取3.7，花港組為新地層，故選擇為3.7。

X1井、X2井自然伽馬曲線計算地層泥質含量圖如圖1、圖2所示。

圖1、圖2分別為X1井、X2井利用自然伽馬曲線計算地層泥質含量的歸一化數值。X1井選取3650～4050m共400m儲層進行示意，X2井選取3200～3600m共400m儲層進行示意。從圖中可以看到，自然伽馬曲線與地層泥質含量具有良好的正相關性，即自然伽馬曲線數值較高處地層泥質含量也較高。利用所計算地層泥質含量可以精確劃分儲層并有效評價儲層的性質和質量。

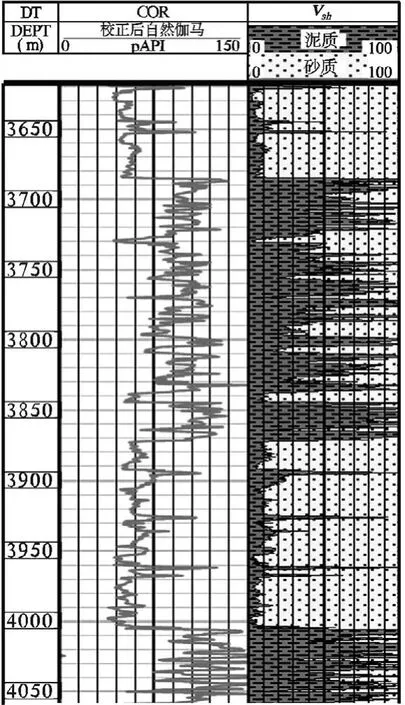
圖1 X1井自然伽馬曲線計算地層泥質含量圖

圖2 X2井自然伽馬曲線計算地層泥質含量圖

2.2 孔隙度解釋模型

孔隙度是反映儲層物性的重要參數，也是儲量、產能計算及測井解釋不可缺少的參數之一[3]。由于孔隙度曲線的測井地質基礎及測井機理不盡相同，孔隙度曲線縱橫向分辨率受井眼及儲層流體性質等非孔隙性因素的影響程度有較大差異[4]。

此項工作利用實驗室進行巖芯分析資料所得到的孔隙度與測井所得到的縱波聲波時差—密度曲線進行回歸分析。將巖芯歸位后的孔隙度與縱波聲波時差—密度交會，得到交會圖及二元一次回歸方程：

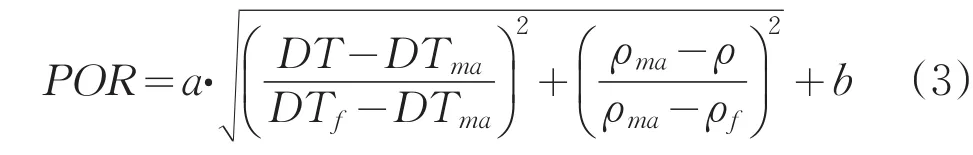
式中：DTma——目的層聲波時差值，55.47μs/ft；

DTf--巖石骨架聲波時差值，188.98μs/ft；

DT——流體時差值，μs/ft；

ρ——目的層密度值，g/cm3；

ρma——巖石骨架密度值，2.65g/cm3；

ρf——流體密度值，1.0g/cm3。

巖芯分析所得孔隙度與縱波聲波時差—密度交會圖如圖3、圖4所示。

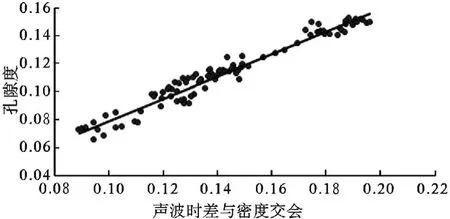
圖3 X1井聲波時差與密度交會法

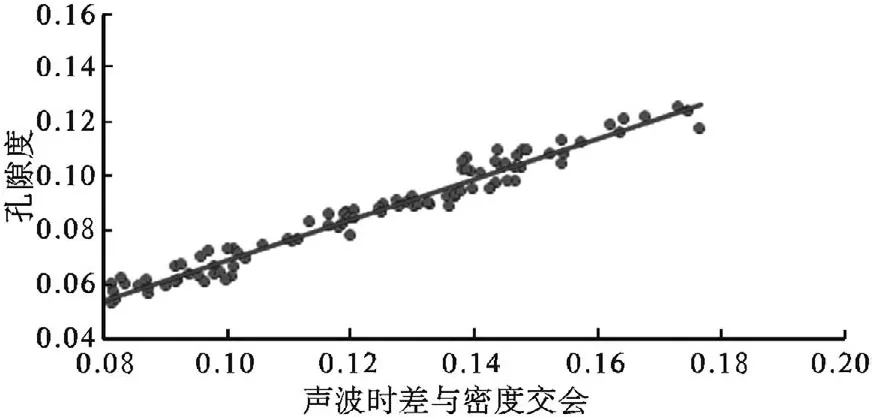
圖4 X2井聲波時差與密度交會法

圖3、圖4是利用西湖凹陷某區塊X1、X2井的經過巖芯歸位、標準化處理、歸一化處理的某層位的縱波聲波時差DT、密度RHOB與實驗室巖芯分析得到的孔隙度POR進行交會得到的關系圖，得到的回歸方程為：

POR=0.7945×

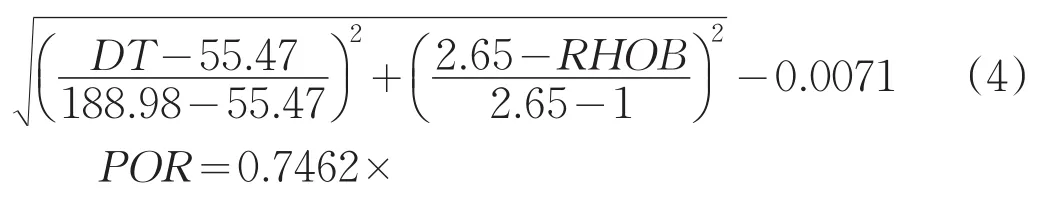
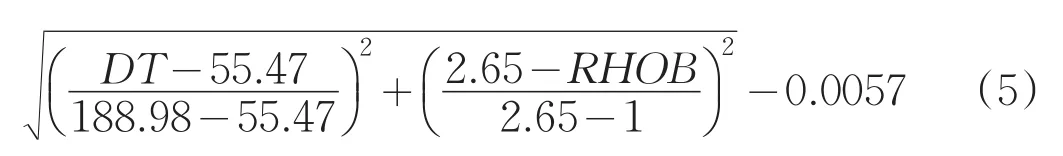
相關系數分別為R2=0.9557、R2=0.9684，一般認為相關系數R2＞0.8即為此關系式可信度較高，因為此關系式可信。

西湖凹陷某區塊儲層巖石結構復雜，利用測井資料直接計算孔隙度有一定的困難。經綜合分析可以看出，若條件允許可利用多條曲線計算孔隙度時，在該工區優先選取縱波聲波時差—密度曲線進行孔隙度計算。

2.3 滲透率解釋模型

巖石的滲透率是指巖層在一定的壓差下允許流體通過的能力，它是評價油層好壞的重要指標之一，確定巖層滲透率是測井資料定量解釋的重要任務之一[5]。而滲透率的大小由儲層孔隙度的大小以及孔隙結構特征共同決定，且儲層孔隙的幾何形態和大小也會影響滲透率。由于孔隙度與滲透率一般呈正相關性，因此實際工作中常常利用孔隙度采取統計方法計算滲透率。

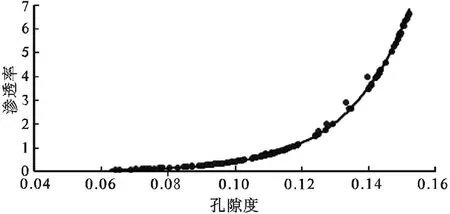
對于西湖凹陷某區塊低孔低滲的儲層特征，經分析得知孔隙度與滲透率相關性較好，因此利用孔隙度為自變量與滲透率做交會圖并求取進行回歸方程。此項工作利用實驗室進行巖芯分析資料所得到的孔隙度與滲透率進行回歸分析，做孔隙度與滲透率交會圖并得到指數函數：

巖芯分析所得孔隙度與滲透率交會圖如圖5、圖6所示。

圖5、圖6是利用西湖凹陷某區塊X1、X2井的經過實驗室巖芯分析得到的孔隙度POR與滲透率PERM進行交會得到的關系圖，得到的回歸方程為：

相關系數分別為R2=0.9984、R2=0.9972，一般認為相關系數R2＞0.8即為此關系式可信度較高，因為此關系式可信。

2.4 含水飽和度解釋模型

含水飽和度Sw和含氣飽和度Sg是評價儲層含氣性的主要標志。由于目前西湖凹陷某區塊無巖芯分析含氣飽和度數據，因此通過研究儲層的含水飽和度來實現。含水飽和度是水的體積在儲層巖石的孔隙的體積中所占的比例，是評價儲層的一個基本參數。

考慮泥質對巖石電阻率的影響,1983年法國Si?mandoux對砂和粘土組成的人工介質做了廣泛的實驗研究,得出泥質砂巖電導率關系式：

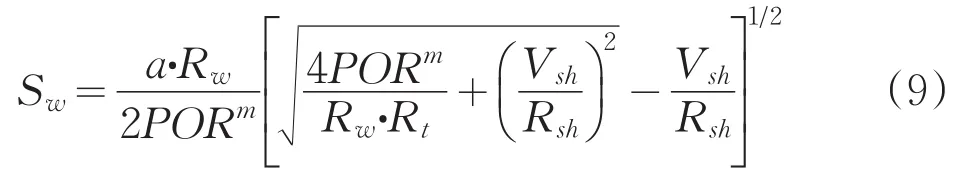
該式是混合泥質砂巖模型，是一種反映含分散泥質的巖石導電性模型[7]。其中Vsh為泥質含量，Rsh為泥質電阻率。Simandoux公式在實際應用中不考慮泥質和粘土的具體分散形式，并認為泥質和純砂巖一樣含有水和氣，這與實際情況較為吻合，這樣也能夠消除儲層物性差異所帶來的影響。在實際計算含水飽和度過程中，巖性系數b和飽和度指數n變化范圍較大，Si?mandoux公式沒有采用這兩個參數，減少了可能出現的誤差。

因此，針對西湖凹陷某區塊的低孔低滲儲層以及泥質含量較高的的地質條件，采用Simandoux公式計算含水飽和度的準確略更高。

3 測井解釋模型檢驗

測井解釋成果圖如圖7所示。

從左至右分別為泥質含量、孔隙度、滲透率、含水飽和度，其中滲透率用對數方式顯示，其余采用百分比形式顯示。從圖中顯示看出，所計算的測井解釋模型與實測數據及地下真是情況基本對應一致。

4 結論

應用所建立的測井解釋模型，對西湖凹陷某區塊的測井資料進行了處理和解釋，為此工區儲層評價提供了地質依據和油藏描述的基礎。根據巖芯分析資料、地質資料、測井資料建立了較為精確的測井解釋模型，有效提高了西湖凹陷某區塊低孔滲儲層的解釋準確率，為下一步的勘探開發提供了可靠的依據。

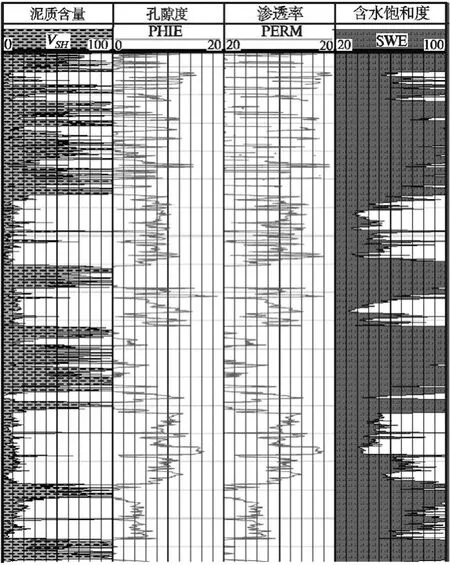
圖7 測井解釋成果圖

[1]曹嘉酋，劉士安，高敏.測井資料綜合解釋[M].北京：石油工業出版社，2002.

[2]尚作源，歐陽健.測井新技術與油氣層評價進展[M].北京：石油工業出版社，1998.

[3]黎文清.油氣田開發地質基礎[M].北京：石油工業出版社，1993.

[4]洪斌.蘇里格氣田蘇X區塊測井儲層評價[D].成都理工大學碩士學位論文，2009：26-35.

[5]王會麗.金湖凹陷低孔低滲儲層分布與測井評價方法研究[D].中國石油大學碩士學位論文，2011：27-42.

[6]張海濤.蘇格里地區有效儲層測井識別方法研究[D].西北大學博士學位論文，2010：67-73.

[7]雍世和，張超謨.測井數據處理與綜合解釋[M].東營:石油大學出版社,1996.

[8]林承焰.樂安油田草4塊Es4稠油油藏測井解釋模型研究[J].西南石油大學學報，2008，30（4）：2-5.

[9]胡楊，等.大牛地氣田測井解釋模型建立與氣層識別標準研究［J］.石油地質與工程，2008，22（3）：37-41.

[10]孫建孟.應用巖心分析資料建立測井解釋模型［J］.石油大學學報：自然科學版，1995，19（4）：28-34.

TN929.5

A

1004-5716(2016)12-0008-04

2016-01-25

2016-01-26

李鈞軻（1990-），男（漢族），天津人，中國海洋大學讀碩士研究生，研究方向：油氣田與煤田地球物理勘探。