電動鉆機頂驅轉盤彈性負載研究

張天生

（天水電氣傳動研究所有限責任公司，甘肅天水741020）

電動鉆機頂驅轉盤彈性負載研究

張天生

（天水電氣傳動研究所有限責任公司，甘肅天水741020）

頂驅／轉盤驅動的鉆具是一個典型的彈性負載，鉆井作業時在鉆具上儲藏了大量的彈性能，此負載特性對控制系統的影響較大。基于此，建立頂驅／轉盤所驅動的這種彈性負載的數學模型，推導出了系統的開環和閉環傳遞函數，從特征方程解析系統的極點分布情況，得出系統穩定的必要條件。采用頻域法分析了系統特性，彈性負載在系統中引入二階振蕩環節，其彈性軸的固有振蕩頻率對系統的穩定性有影響，是潛在振蕩隱患，提出了改善系統性能的辦法。

彈性負載；數學模型；傳遞函數；機械諧振；振蕩環節；頻域法；穩定性

1 概述

頂驅／轉盤是鉆機旋轉系統的驅動者，鉆井深度從數千米到上萬米不等，驅動系統拖動鉆具長度不斷變化的彈性體在地殼中旋轉，鉆頭在井底切削巖層，鉆具受到的粘滑轉矩與地質構造、泥漿配比等有關，轉動慣量與鉆具長度有關，在鉆井作業時鉆具上儲藏的彈性轉矩能是K（θd－θl），經推導可將這種彈性鉆具等效為二階振蕩環節，這種彈性旋轉系統參數變化范圍大，并因地質構造的變化還存在一定的不確定因素，會對系統的穩定性造成不良影響，本文就如何消除或減弱這種不利因素，展開控制策略的討論，對系統的動態和靜態響應等指標進行理論推導和計算。本文以直流頂驅系統為例，電機采用它勵直流電機（GE752），進行建模和推導。

2 數學模型

依據轉矩平衡和電壓平衡關系建立系統運動方程如下。

頂驅／轉盤軸端轉矩平衡的微分方程：

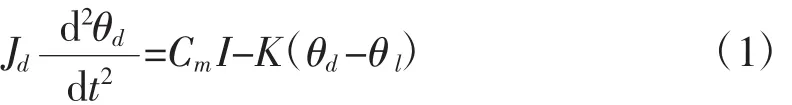
鉆頭軸端轉矩平衡的微分方程：

電機端電壓平衡的微分方程：

式中：Jd為頂驅／轉盤軸端轉動慣量，kg·m2；

Jl為鉆頭軸端轉動慣量，kg·m2；

θd為頂驅／轉盤軸端的旋轉角，rad；

θl為鉆頭軸端的旋轉角，rad；

K為彈性系數，N·m／rad；

Df為粘性摩擦系數，N·m·s／rad；

Tl為負載擾動轉矩，N·m；

Cm＝CMΦ，CM為轉矩常數，Φ為磁通；

由 CM＝9.55Ce，得 C＝Cm

I為電樞電流，A；

R為電樞電阻，Ω。

對上述微分方程進行拉普拉氏變換得：

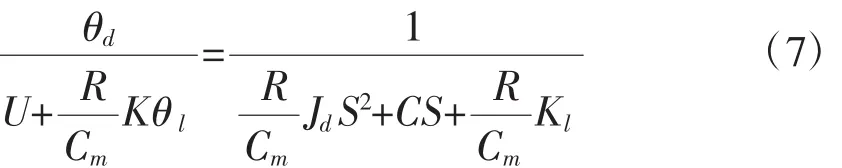
式（5）變形得：

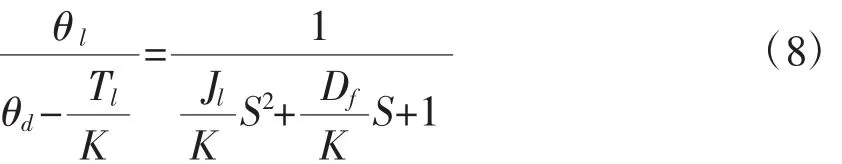
3 傳遞函數

由式（7）得傳遞函數框圖如圖1所示。

圖1 由式（7）得傳遞函數框圖

由式（8）得傳遞函數框圖如圖2所示。

圖2 由式（8）得傳遞函數框圖

合并框圖1和框圖2得到傳遞函數框圖如圖3所示。

圖3 合并框圖1和框圖2得傳遞函數框圖

為了研究負載擾動作用下系統的運動情況，令U＝0，經結構變換得如圖4所示框圖，以便研究鉆頭旋轉角θl與負載擾動轉矩Tl之間的關系。

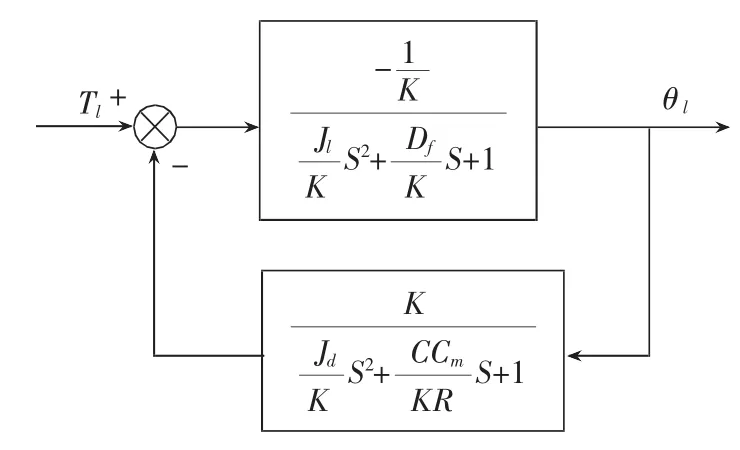
圖4 鉆頭旋轉角與負載擾動之間的傳遞函數框圖

系統開環傳遞函數：

開環頻率特性函數：

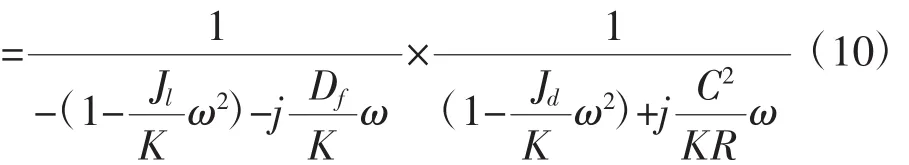
幅頻特性函數：

開環對數幅頻特性函數：

相頻特性函數：

Bode圖的繪制：

以μ為橫坐標（μ＝lgω）、lgH0（G）和argH0（jω）分別為縱坐標繪制對數幅頻特性和相頻特性圖（Bode圖），這種做圖法比較直觀，參數變化對系統動態性能的影響在Bode圖上就能直接看到其變化趨勢，可以很方便地分析系統的運動情況。系統的截止頻率ωc就是對數幅頻特性穿過零分貝線的頻率，它反映了系統的快速性，ωc值大快速性就好；為了提高系統的抗擾能力，在對數幅頻特性的高頻區衰減應盡可能快些，彈性負載的固有振蕩頻率ω0就出現在這一區間，Bode圖示便于分析，得出解決方法。

系統閉環傳遞函數：

把上述傳遞函數寫成標準形式：

從傳遞函數可以看出，微分方程的特征方程的所有系數是同號的，表明特征方程的根是負實數或實部為負的共軛復數，即全部根都位于復數平面的左半面，這只是系統穩定的必要條件，而不是充分條件。系統的穩定性取決于特征方程，各系數完全是由系統本身的結構和參數決定的。

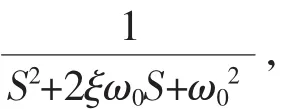
4 特性分析

若彈性系數K＝∞是鋼性系統，實際的彈性系數K隨著鉆具的加長而變小，ω0也越低，這時ω0接近于系統的截止頻率ωc，在ω0處開環對數幅頻特性的諧振峰值若穿過零分貝線，系統就出現振蕩，產生軸扭振。若未穿過零分貝線，這時振蕩峰值離零分貝線的距離就是穩定余量。

系統的截止頻率ωc是反應動態響應的重要指標，ωc越高，響應越快，彈性系數K變小；ω0越低，ωc與ω0相近，出現軸扭振的機會越多。鉆井作業時往往通過降低動態響應的方法，即變小截止頻率ωc，來防止出現振蕩。

理論上可以設計二階校正網絡，利用網絡的復零點與振蕩環節的復極點對消，來改善系統的穩定性。校正網絡的傳遞函數寫成標準形式：

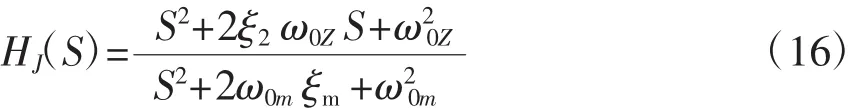
要求 ω0Z＝ω0，ξZ＝ξ。

頂驅轉盤負載的這種彈性振蕩一般是低阻尼的，對消后系統增加兩個慣性環節，在ω0處系統的開環對數幅頻特性的諧振峰值不穿越零分貝線，系統變得穩定。但在實際工程中很難實現，因為ω0、ξ是不斷變化的。

在轉速反饋通道中阻止ω0附近頻率范圍內的信號通過，能減小系統開環對數幅頻特性在ω0處的幅值，不致穿越零分貝線，擬制振蕩，截止頻率ωc不變，不影響系統的快速性。

采用復合控制提高系統的抗擾能力，利用可測量參數電流、轉矩、速度推算負載擾動，前饋控制（開環）＋反饋控制（閉環）。增加前饋控制不影響原系統的穩定性，提高了系統的穩態精度，引入與負載轉矩變化量正比例的信號，作為前饋信號，補償轉矩誤差。

引入速度反饋的比例微分控制，可以使系統超調小、振蕩輕、恢復穩態快。從負載力矩變化量的方向與驅動速度的關系來考慮，引入與鉆具的擾動力矩變化反向的速度反饋信號，振蕩就會迅速衰減下來，對系統穩定有利。

5 結束語

本文對電動鉆機頂驅轉盤彈性負載進行了研究，得出了以下結論。

（1）在滿足鉆井工況要求的情況下，降低系統的動態指標，使系統的截止頻率ωc變小，防止彈性負載出現扭振。

（2）引入復合控制，采用前饋控制＋反饋控制的方式，補償系統誤差。

（3）轉速反饋通道濾波，減小開環對數幅頻特性在ω0處的諧振峰值，防止振蕩出現。

（4）速度反饋環節引入比例微分控制負反饋，衰減振蕩。

（5）增加串聯校正網絡，利用零點與極點對消的方式，改善系統的穩定性。

［1］顧繩谷.電機及拖動基礎［M］.北京：機械工業出版社，1990.

［2］天津電氣傳動設計研究所.電氣傳動自動化技術手冊［M］.北京：機械工業出版社，2007.

［3］吳 麒.自動控制原理［M］.北京：清華大學出版社.

Research on elastic load for top drive rotary table of electric drilling rig

ZHANG Tian－sheng

（Tianshui Electric Drive Research Institute Co.，Ltd.，Tianshui 741020，China）

The drilling tool of the electric drilling rig driven by the top drive rotary table is a typical elastic load，which stores a large amount of elastic energy when doing the drilling works.It has great influence on the performance of the control system of the drilling rig.Therefore，a mathematical model is established，and its closed－loop and open－loop transfer functions are also derived.In this way，the necessary conditions of the system stability are obtained according to the poles distribution by the characteristic equations.Based on the frequency domain method，the second orderoscillationlinkisemployedintheelasticloadsystem.However，the system stability is deteriorated by the inherent oscillation frequency of the elastic axis，a novel method that can improve the system performance is put forward.

elastic load；mathematical model；transfer functions；mechanical resonance；oscillation link；frequency domain method；stability

TE922

A

1005—7277（2016）05—0001—03

張天生（1964－），男，本科，正高級工程師，從事電動鉆機控制系統的開發研制工作。

2016－08－01