二端口波混沌腔體短跡線隨機耦合模型

李福林 韓繼紅 張暢

(1.解放軍信息工程大學,鄭州 450001;2.軍隊信息安全重點實驗室,鄭州 450001)

?

二端口波混沌腔體短跡線隨機耦合模型

李福林1,2韓繼紅1,2張暢1

(1.解放軍信息工程大學,鄭州 450001;2.軍隊信息安全重點實驗室,鄭州 450001)

經典隨機耦合模型在對電子設備的電磁脈沖效應進行預測時,邊界條件設置在無窮遠處,存在短跡線效應問題.采用設置輻射阻抗短跡線調制系數的方法,建立了二端口波混沌腔體短跡線隨機耦合模型(Short-Orbit Random Coupling Model,SORCM),統計分析了目標點處感應電壓的均方根誤差隨短跡線最大長度的變化關系.在不同的頻段范圍內,將SORCM計算結果的統計特性和實驗結果進行了對比分析,驗證了所建立模型的正確性.和經典隨機耦合模型相比,SORCM的計算結果更加接近實測結果,可用于復雜電子設備電磁脈沖效應的預測和分析.

波混沌腔體;電磁脈沖效應;SORCM;輻射阻抗

DOI 10.13443/j.cjors.2016070501

引 言

隨著電子技術的高速發展,大規模集成電路技術在各類電子設備中廣泛應用,在提高電子設備處理能力的同時,也使得這些設備的電磁敏感度越來越高[1].超寬帶(Ultra-Wideband, UWB)、高功率微波(High Power Microwave,HPM)等強電磁脈沖通過瞬態干擾、微波加溫、高壓擊穿、電涌沖擊等模式,造成電子元器件性能下降、狀態反轉、結點擊穿、器件燒毀,妨礙電子設備的正常運行和作用發揮.開展電磁脈沖效應規律研究對于探索相應的防護措施、增強電子設備的生存能力具有重要意義.

由于電子設備內部結構的復雜性,其電磁脈沖效應問題較為復雜,難以用解析方法建立電動力學方程,運用時域有限差分(Finite Difference Time Domain,FDTD)法[2]、有限元法(Finite Element Method,FEM)[3]、矩量法(Method of Moments, MoM)[4]等數值計算方法求解需要耗費大量的計算資源,有時甚至無法求得問題的解.采用電磁拓撲法[5-7]將系統分解為多個子電磁空間,求解仍然十分復雜,且所建立的電磁拓撲模型與被分析個體緊密相關,難以推廣到同類其他電子設備.采用傳輸線矩陣(Transmission Line Matrix,TLM)法[8]在對低頻段的電磁干擾信號進行分析時行之有效,但當電磁波頻率較高時,場的波動性明顯增強,很難用集總參數進行有效的描述.

美國馬里蘭大學的Xing Zheng、Sameer Hemmady等人基于隨機平面波假說和隨機矩陣理論,提出了隨機耦合模型(Random Coupling Model, RCM)[9-10],用統計學的方法對腔體內目標點的電磁效應物理量進行概率性的預測,對特定目標的研究結果可以給其他具有相似結構的系統提供參考,為復雜設備的電磁能量耦合分析提供了一種新的思路和方法[11].在國內,許多學者對RCM進行了研究和實驗驗證,閆二艷等人運用RCM對計算機機箱腔體內電磁效應物理量的統計特性進行了研究[12-13],莊信武等人總結了矩形、球形及其布爾組合體的混沌統計特性規律[14-15],陸希成等人基于天線輻射理論構建微波混沌腔的隨機耦合模型[16],郝建紅、范杰清、宋子賢等人運用RCM對一種調頻發射電路目標點的電壓概率密度進行了分析[17-19].

經典RCM在對輻射阻抗矩陣(radiation impedance matrix)的計算過程中,邊界條件設置在無窮遠處,等效于腔體側壁邊界為理想吸波材料,在這種情況下,沒有任何反射波回到激勵孔.但實際的電子設備內壁不會是理想的吸波材料,總有一些反射波會回到激勵孔,這些反射波的軌跡被稱為“短射線軌跡”(簡稱為短跡線，Short-orbit).由于短跡線效應的存在,經典RCM計算所得的目標點電壓統計結果和實際測量統計結果的變化趨勢基本一致,但二者的峰值有偏差.文獻[12]在對經典RCM進行實驗驗證時,發現存在短跡線效應問題,但未給出解決該問題的方法.文獻[14]提出了短跡線耦合技術,但未給出詳細的解決方案,且未針對具體的混沌腔體開展實驗驗證.文獻[20-23]只對腔體內單目標點的短跡線效應問題進行了研究,且未給出目標點感應電壓統計分析的具體結果.用統計的方法對混沌腔體內的電磁效應物理量實施建模,其精度與射線軌跡是否充分遍歷整個混沌腔體有關.解決短跡線效應問題的關鍵是分析短跡線屬性與電磁效應物理量的關系,本文通過定義輻射阻抗短跡線調制系數的方法建立了輻射阻抗和短跡線屬性的關系,給出了輻射阻抗短跡線調制系數的計算方法,并對該方法在二端口波混沌腔體條件下進行了實驗驗證.

1 理論分析

1.1 隨機耦合模型

經典RCM指出:對于復雜的波混沌腔體,其內部電磁參量可以分為通用統計特性和非通用統計特性兩部分,對于二端口有損金屬腔體,用Zcav表示其腔體阻抗矩陣,則Zcav可由式(1)進行描述[9-10]:

(1)

式中：Zrad代表腔體的自由空間輻射阻抗;Znor代表腔體的歸一化阻抗.

腔體的自由空間輻射阻抗Zrad可由式(2)得出:

(2)

式中：Z0為實對角矩陣,其元素為連接激勵孔傳輸線的特征阻抗;I2×2為2×2的單位矩陣;Srad為腔體的輻射散射系數,可通過電磁仿真軟件或直接測量獲得.

腔體的歸一化阻抗Znor可由式(3)得出:

(3)

式中：W是一個2×M的耦合矩陣, M為二端口波混沌腔體的模數,元素Wij描述第i個激勵源與腔體第j個本征模之間的耦合,Wij是滿足方差為1、均值為0的獨立高斯分布的隨機數;WT代表W的轉置矩陣;P為M×M的對角矩陣,其目的是產生M個特征值,這些特征值滿足Wigner半圓分布;I為M×M的單位矩陣;α為腔體損耗因子,可由公式法或直接比較法求得[19].

1.2 二端口波混沌腔體短跡線隨機耦合模型

經典RCM在使用式(2)計算腔體輻射阻抗Zrad時,將腔體側壁邊界等效為理想吸波材料,未考慮實際電子設備存在的短跡線軌跡.為建立電磁效應物理量和短跡線屬性的關系.定義輻射阻抗Zrad的短跡線調制系數ξ=ρ+jx,存在短跡線時的輻射阻抗用Zsoc表示,則有

(4)

Zsoc的實部和Zrad的實部滿足

(5)

Zsoc的虛部和Zrad的虛部滿足

(6)

考慮短跡線效應后,計算腔體阻抗的式(1)可用式(7)表示:

(7)

式(4)～(7)稱為波混沌腔體短跡線隨機耦合模型(Short-orbit Random Coupling Model, SORCM).

下面推導準二維波混沌腔體輻射阻抗短跡線調制系數ξ的解析表達式.定義如圖1所示的準二維波混沌腔體,高度h遠小于入射波長,假設電場只沿z方向傳播.

圖1 準二維腔體截面

由經典RCM,端口m和n之間的阻抗可表示為

Zm,n=

(8)

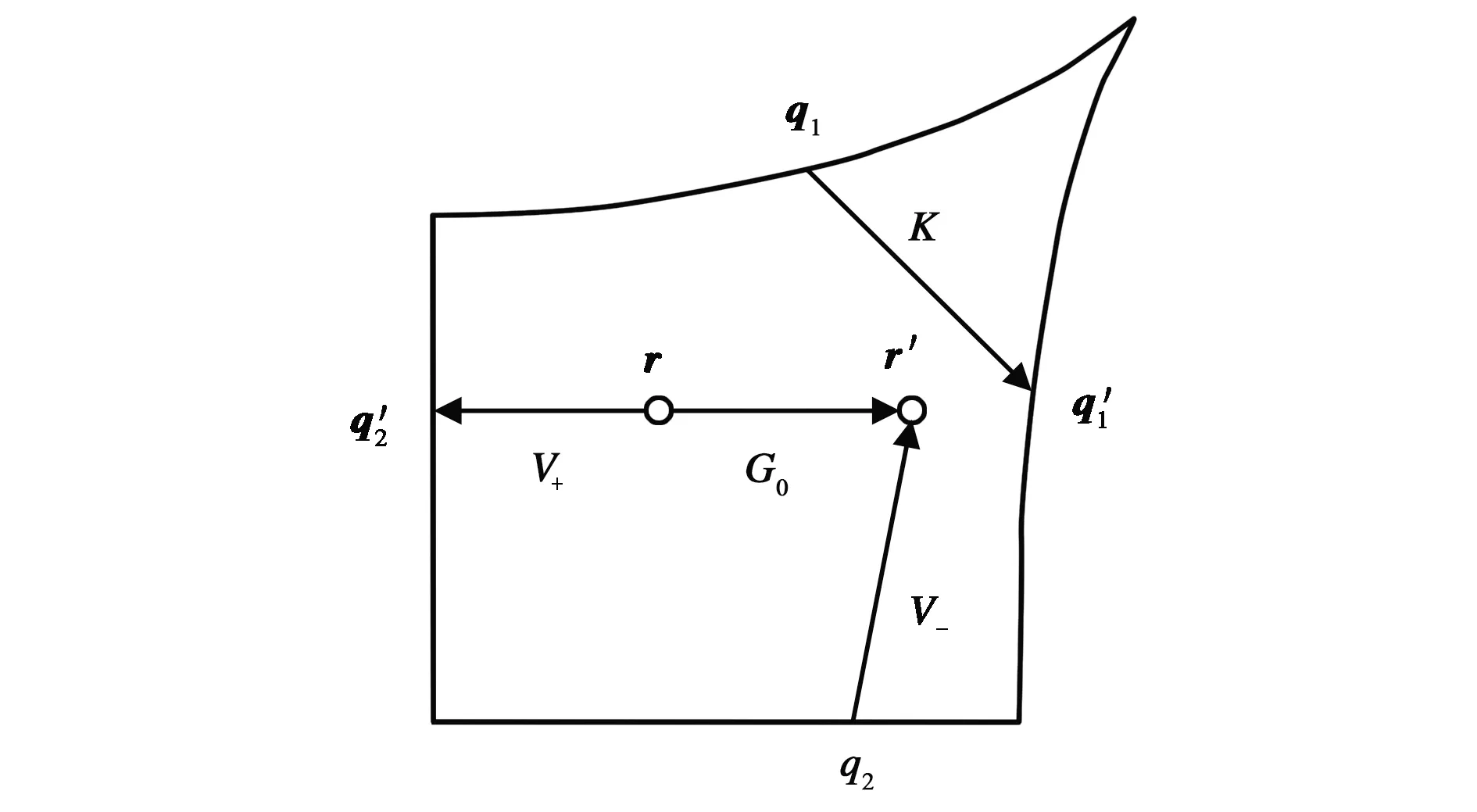
圖2 運算符V-、V+、K、G0示意圖

為考慮RCM的短跡線效應,定義M×M的矩陣Z,其元素為Zm,n由式(9)表示:

Zm,n=jkhη∫d2rum(r)G0un(r),

(9)

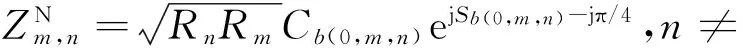
(10)

式(10)中的各個子項滿足式(11)～(13):

(11)

=khη∫∫d2run(r)[V-(K)β-1V+]um(r);

(12)

(13)

式(11)中,θ為跡線的反彈入射角,矩陣θ為

θ=[cos(θ),sin(θ)].

(14)

式(13)中的Db(β,m,n)表示跡線b(β,m,n)的穩定系數,為

(15)

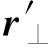
由式(9)～(15)可得在腔體有損耗的情況下,端口m和n之間的短跡線調制系數為

(16)

式中：Lb(β,m,n)為跡線b(β,m,n)的長度,設其最大值為LM;Lp(β,m,n)為端口m和端口n之間的距離;k′=k/(2Q)為有效衰減參數,Q為腔體的品質因子;pb(β,m,n)是跡線b(β,m,n)在系綜中出現的概率.

將式(16)代入式(4)后,再將式(4)代入式(7),即可得到考慮短跡線情況下腔體阻抗的計算公式.

2 實驗過程與結果分析

以某電子設備作為實驗箱體,其長、寬、高尺寸分別為48.2 cm、45.0 cm、17.8 cm.以箱體的右下外側頂點為原點建立坐標系,如圖3所示,孔1位于坐標(0,22.5,8.9)處,取三個目標點A、B、C分別位于坐標(24.1,22.5,8.9)、(36.2,22.5,8.9)、(36.2,11.5,4.5)處.

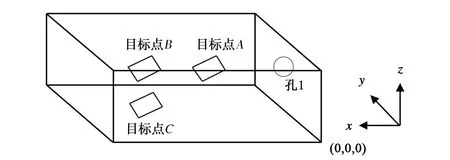
圖3 實驗箱體模型

2.1 實驗環境與實驗過程

2.1.1 腔體散射矩陣的測量

腔體散射矩陣的測量環境如圖4所示.

為加強射線的混沌特性,基于“模式攪拌理論”,在腔體內部放置一個模式攪拌槳,該槳由一個直徑為2 cm的圓柱體和三個間隔為5 cm、尺寸為6 cm×3 cm的葉片組成.在孔1和目標點之間連接矢量網絡分析儀,在頻率范圍為4.9～5.1 GHz和5.9～6.1 GHz兩個頻段內,采取模式攪拌的方法,每隔1 MHz為一個采樣點,每10°旋轉一次攪拌槳,共旋轉2周,對每個目標點,都可以獲取腔體散射矩陣2×200×72的系綜實驗數據.

圖4 散射矩陣測量環境示意圖

2.1.2 腔體輻射散射矩陣的測量

腔體輻射散射矩陣是激勵進入腔體后沒有反射情況下的散射矩陣,因此在測量輻射散射矩陣時,將圖4中實驗腔體的內壁覆蓋吸波材料,移除攪拌槳,在同樣的頻段內,每隔1 MHz為一個采樣點,在不同的時間、相同的實驗條件下做30次測量,對每個目標點,獲取腔體輻射散射矩陣2×200×30的系綜實驗數據.

2.1.3 目標點感應電壓的測量

斷開圖4中矢量網絡分析儀和實驗箱體的連接,激勵孔1連接信號發生器和功率放大器,目標點連接示波器,在同樣的頻段內,采用同樣的頻點采樣方法和模式攪拌方法,通過示波器獲取每個目標點感應電壓2×200×72的系綜實驗數據.

2.2 目標點感應電壓計算方法

結合微波雙端口網絡中阻抗參量的概念,在分別考察每個目標點的感應電壓時,可將圖3所示的腔體結構抽象為如圖5所示的雙端口微波網絡.

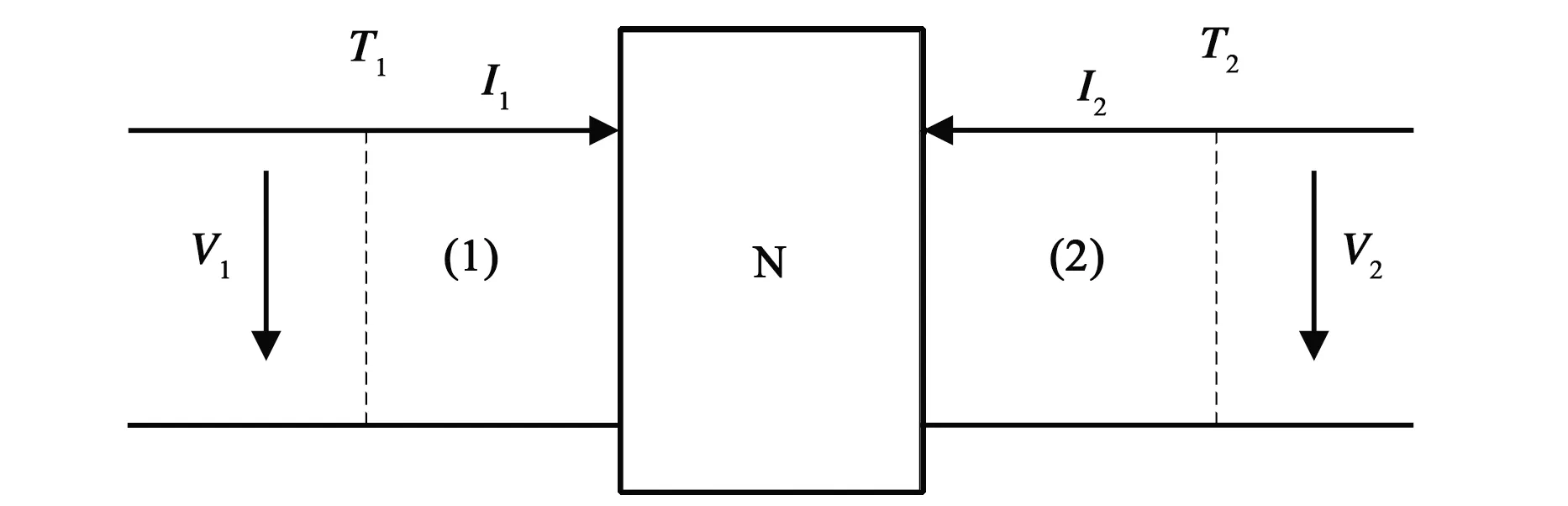
圖5 雙端口微波網絡等效電壓、電流示意圖

對圖5所示的雙端口微波網絡,等效電壓、電流與阻抗的關系可表示為

(17)

腔體阻抗可表示為一個2×2矩陣:

(18)

在目標點開路的情況下,可由孔1的輻射功率頻譜分布求得目標點處感應電壓V2的統計分布:

(19)

式中,P1(f)為孔1處激勵信號的功率密度分布函數.

2.3 短跡線最大長度確定方法

短跡線長度的含義是“從電磁波進入腔體,經若干次反射,直至其離開腔體所經過路徑長度的總和”[23],理論上短跡線最大長度的取值范圍為(0,+∞),短跡線最大長度的取值越大,式(16)計算時所包含的短跡線數目也就越多,SORCM的計算結果越準確,但相應的計算時間也就越長.在工程應用中,需要結合實際,確定一個短跡線最大長度的門限值.

文章通過分析目標點感應電壓的均方根誤差隨短跡線最大長度變化關系的方法,來確定滿足要求的短跡線最大長度門限值.定義目標點處感應電壓V2的均方根誤差eRMS為

(20)

式中：n為樣本總數;〈Vi〉為Vi的平均值.

目標點處感應電壓V2的eRMS隨短跡線最大長度LM的變化情況如圖6所示.

圖6 eRMS隨短跡線最大長度的變化情況

工程應用中要求目標點處感應電壓的均方根誤差小于0.013,從圖6可以看出,當eRMS的取值為0.013時,對應的LM值為90 cm.當LM的取值大于90 cm時,可以滿足均方根誤差小于0.013的要求.為簡化計算量,在本文的實驗條件下,選擇LM為90 cm.

2.4 短跡線隨機耦合模型計算結果分析

對如圖3所示的腔體,對目標點A,采用2.1節的實驗方法,注入功率P1(f)=1 W,Lp(1,2)=24.1 cm,由2.3節的分析,選擇短跡線的最大長度LM為90 cm,采用隨機矩陣蒙特卡羅法[18]確定腔體的損耗因子α,分別采用經典RCM的式(1)、短跡線隨機耦合模型SORCM的式(7)計算腔體阻抗,由式(19)計算目標點的感應電壓V2在兩種模型下的統計分布.

經典RCM、SORCM和實驗測量統計結果的對比情況如圖7、8所示.

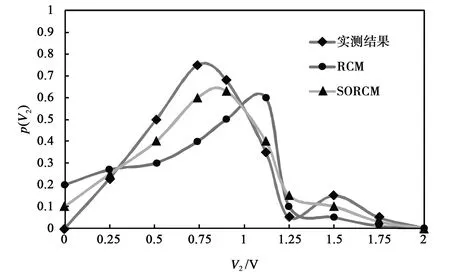
圖7 4.9～5.1 GHz目標點A感應電壓統計分布

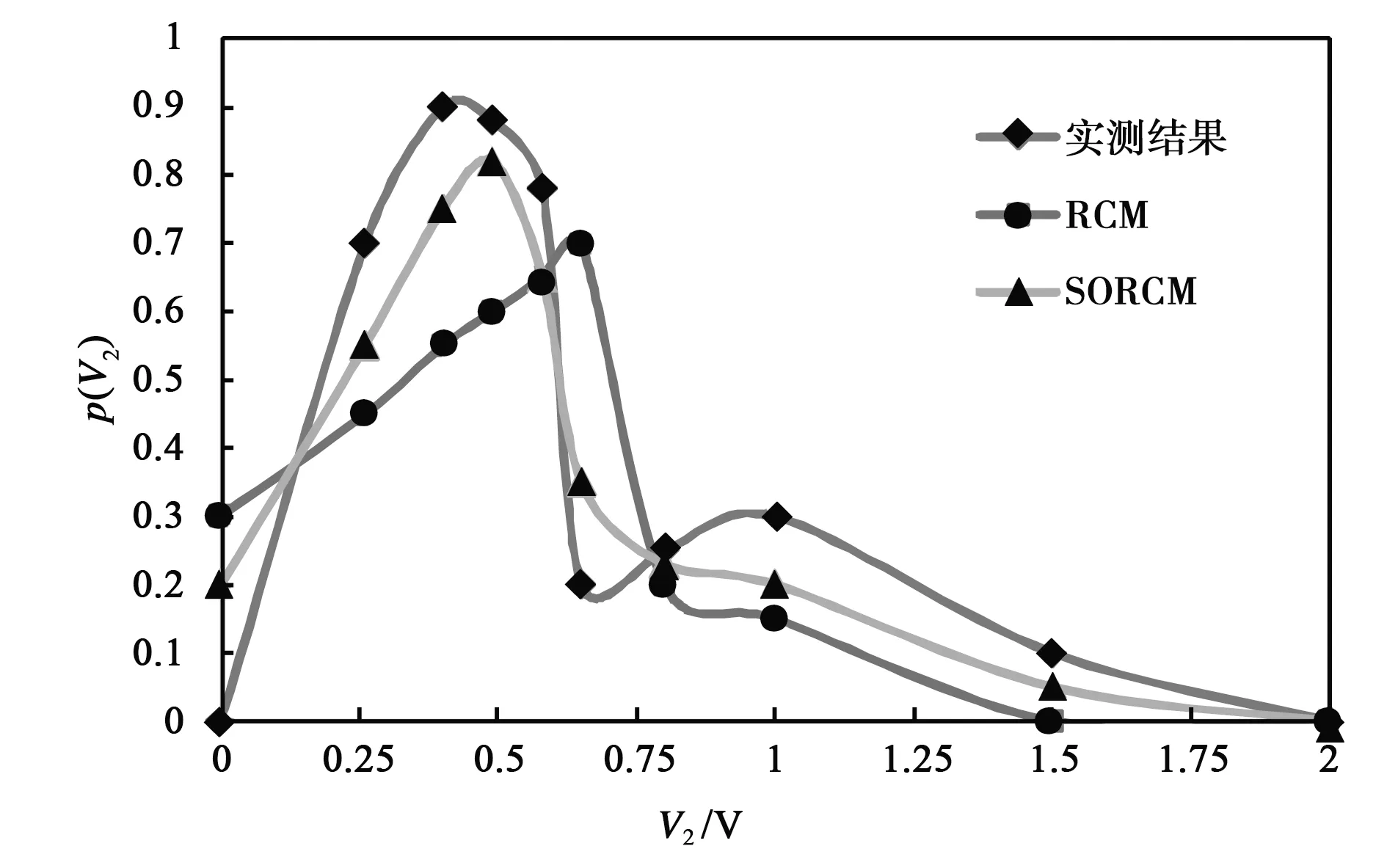
圖8 5.9～6.1 GHz目標點A感應電壓統計分布

從圖7可以看出,在4.9～5.1 GHz頻段范圍內,實測結果、經典RCM計算結果、SORCM計算結果得到的目標點A處感應電壓值的最大概率分別出現在0.74 V、1.12 V和0.90 V.經典RCM在對輻射阻抗的計算過程中,邊界條件設置在無窮遠處,等效為腔體側壁為理想吸波材料,所有進入腔體的電磁波都被設備充分吸收,因此和SORCM相比,計算結果偏大,而SORCM考慮了散射系統的短跡線屬性,計算結果更加接近實測值.從圖8可以看出,在5.9～6.1 GHz頻段范圍內,實測結果、經典RCM計算結果、SORCM計算結果得到的目標點A處感應電壓值的最大概率分別出現在0.40 V、0.65 V和0.49 V,同樣,SORCM的計算結果更加接近實測結果.對目標點B和目標點C的實驗結果進行統計分析,可以得出與目標點A一致的結論.

在實驗的頻段范圍內采用SORCM方法分別計算目標點A、B和C感應電壓的概率密度,結果如圖9、10所示.

比較圖9和圖10中三個目標點概率最大的感應電壓值,可以看出:在4.9～5.1 GHz頻段范圍內,目標點A最大,為0.90 V,其次是目標點B,為0.74 V,目標點C最小,為0.51 V;在5.9～6.1 GHz頻段范圍內,同樣是目標點A最大,為0.49 V,其次是目標點B,為0.40 V,目標點C最小,為0.26 V.其原因是目標點A離激勵孔最近,耦合的能量最大,其次是目標點B,而目標點C距激勵孔最遠,耦合的能量最小.

圖9 4.9～5.1 GHz目標點感應電壓SORCM計算結果

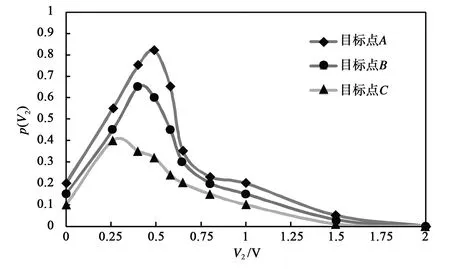
圖10 5.9～6.1 GHz目標點感應電壓SORCM計算結果

3 結 論

通過定義輻射阻抗短跡線調制系數的方法,在4.9～5.1 GHz和5.9～6.1 GHz兩個頻段范圍內,建立了二端口波混沌腔體短跡線隨機耦合模型,統計分析了目標點處感應電壓的均方根誤差隨短跡線最大長度的變化關系,對建立的二端口短跡線隨機耦合模型進行了實驗驗證.結果表明,與經典隨機耦合模型相比,短跡線隨機耦合模型的計算結果更加接近實測結果,能夠更有效地預測復雜電子設備的電磁脈沖效應.論文的研究可進一步促進隨機耦合模型的實際工程應用,為電子設備的電磁安全防護設計提供參考.

[1]劉培國, 劉晨曦, 譚劍鋒, 等.強電磁防護技術研究進展[J].中國艦船研究, 2015, 10(2)：2-6.

LIU P G, LIU C X, TAN J F, et al.Analysis of the research development on HPM/EMP protection[J].Chinese journal of ship research, 2015, 10(2)：2-6.(in Chinese)

[2]HOCKANSON D M, YE X N, DREWNIAK J L, et al.FDTD and experimental investigation of EMI from stacked-card PCB configurations[J].IEEE transactions on electromagnetic compatibility, 2001, 43(1)：1-9.

[3]CARPES W P, PICHON L Jr, RAZEK A.Analysis of the coupling of an incident wave with a wire inside a cavity using an FEM in frequency and time domains[J].IEEE transactions on electromagnetic compatibility, 2002, 44(3)：470-475.

[4]BOGDANOV F G, KARKASHADZE D, JOBAVA R G, et al.Validation of hybrid MoM scheme with included equivalent glass antenna model for handling automotive electromagnetic compatibility problems[J].IEEE transactions on electromagnetic compatibility, 2010, 52(1)：164-172.

[5]闞勇, 閆麗萍, 趙翔, 等.基于電磁拓撲的多腔體屏蔽效能快速算法[J].物理學報, 2016, 65(1)：030702.

KAN Y, YAN L P, ZHAO X, et a1.Electromagnetic topology based fast algorithm for shielding effectiveness estimation of multiple enclosures with apertures [J].Acta physica sinica, 2016, 65(1)：030702.(in Chinese)

[6]王利萍, 周東方, 彭強, 等.基于拓撲網絡的屏蔽腔體內置微帶線響應分析[J].電波科學學報, 2014, 29(1)：321-327.

WANG L P, ZHOU D F, PENG Q, et a1.Response analysis of microstrip lines in the shielding cavity based on topological network[J].Chinese journal of radio science, 2014, 29(1)：321-327.(in Chinese)

[7]YU Q, WANG Y D, HAN J H.The terminal responses of lossy microstrip line illuminated by a plane wave[C]//2011 IEEE International Conference on Microwave Technology &Computational Electromagnetics, 2011, 5：897-900.

[8]張悅, 劉尚合, 胡小鋒, 等.不同輻射源瞬態電磁信號輻射場特性研究[J].電波科學學報, 2015, 30(2)：316-322.

ZHANG Y, LIU S H, HU X F, et a1.Properties of transient electromagnetic signals radiation field from various radiation sources[J].Chinese journal of radio science, 2015, 30(2)：316-322.(in Chinese).

[9]ZHENG X.Statistics of impedance and scattering matrices in chaotic microwave cavities：the random coupling model[D].University of Maryland, 2005.

[10]HEMMADY S D.A wave-chaotic approach to predicting and measuring electromagnetic field quantifies in complicated enclosures[D].University of Maryland, 2006.

[11]劉尚合, 劉衛東.電磁兼容與電磁防護相關研究進展[J].高電壓技術, 2014, 40(6):1605-1613

LIU S H, LIU W D.Progress of relevant research on electromagnetic compatibility and electromagnetic protection[J].High voltage engineering, 2014, 40(6)：1605-1613.(in Chinese)

[12]閆二艷.波混沌腔體中電磁效應物理量的統計特性研究[D].綿陽：中國工程物理研究院, 2009.

YAN E Y.The statistic characteristic research of electromagnetic effect physical quantity in chaotic cavity[D].Mianyang：China Academy of Engineering Physics, 2009.(in Chinese)

[13]閆二艷, 孟凡寶, 馬弘舸.微波混沌腔體中的散射特性研究[J].物理學報, 2010, 59(3)：1568-1675.

YAN E Y, MENG F B, MA H G.Research on scattering in microwave chaotic cavity[J].Acta physica sinica, 2010, 59(3):1568-1675.(in Chinese)

[14]莊信武, 余志勇, 劉光斌, 等.混沌腔體的統計電磁預測技術[J].強激光與電子束, 2014, 26(3):197-203.

ZHUANG X W, YU Z Y, LIU G B, et a1.Electromagnetic statistical prediction of chaotic cavities[J].High power laser and particle beams, 2014, 26(3)：197-203.(in Chinese)

[15]莊信武, 余志勇, 劉光斌, 等.復雜腔體電磁混沌特性統計分析[J].電波科學學報, 2015, 30(3)：597-602.

ZHUANG X W, YU Z Y, LIU G B, et a1.Statistical analysis on EM chaos characteristics for complex cavity[J].Chinese journal of radio science, 2015, 30(3)：597-602.(in Chinese)

[16]陸希成, 王建國, 劉鈺.基于天線輻射理論構建微波混沌腔的隨機耦合模型[J].物理學報, 2013, 62(7)：070504.

LU X C, WANG J G, LIU Y.Based on antenna theory to establish the random coupling model of microwave chaotic cavities[J].Acta physica sinica, 2013, 62(7)：070504.(in Chinese)

[17]郝建紅, 孫娜燕, 高璞, 等.場路結合法分析設備電磁輻照效應[J].電波科學學報, 2012, 27(2)：359-364.

HAO J H, SUN N Y, GAO P, et a1.Analysis of the electromagnetic radiation effect of the equipment by field-circuit method[J].Chinese journal of radio science, 2012, 27(2)：359-364.(in Chinese)

[18]范杰清.復雜金屬腔體高功率微波耦合效應研究[D].北京：華北電力大學, 2015.

FAN J Q.Study on effect of HPM coupling on complex metal cabity[D].Beijing：North China Electric Power University, 2015.(in Chinese)

[19]宋子賢.基于RCM的混沌腔體耦合特性的研究[D].北京：華北電力大學, 2015.

SONG Z X.Analysis of electromagnetic coupling properties for chaotic cavity based on RCM[D].Beijing：North China Electric Power University, 2015.(in Chinese)

[20]HART J A, ANTONSEN T M, OTT E.Effect of short ray trajectories on the scattering statistics of wave chaotic systems[J].Physical review E, 2009, 80：041109.

[21]YEH J H, HART J A, BRADSHAW E, et a1.Experimental examination of the effect of short ray trajectories in two-port wave-chaotic scattering systems[J].Physical review E, 2010, 82:041114.

[22]YEH J H, HART J A, BRADSHAW E, et al.Universal and nonuniversal properties of wave-chaotic scattering systems[J].Physical review E, 2010, 81：025201.

[23]YEH J H.Wave chaotic experiments and models for complicated wave scattering systems[D].University of Maryland, 2013.

李福林 (1979-),男,河北人,解放軍信息工程大學博士研究生,副教授,主要研究方向為電子設備電磁脈沖效應分析.

韓繼紅 (1966-),女,山西人,解放軍信息工程大學教授,博士生導師,博士,主要研究方向為電子設備電磁脈沖效應分析及安全防護、安全協議分析與驗證.

張暢 (1981-),男,湖北人,解放軍信息工程大學博士研究生,講師,主要研究方向為電子設備電磁安全防護.

Short-orbit random coupling model in two-port wave-chaotic cavity

LI Fulin1,2HAN Jihong1,2ZHANG Chang1

(1.PLAInformationEngineeringUniversity,Zhengzhou450001,China;2.PLAKeyLaboratoryofInformationSecurity,Zhengzhou450001,China)

The traditional random coupling model sets boundary conditions at infinity in calculating the effect of electromagnetic pulse with the electronic equipment, which causes a problem named short-orbit effects.In order to decrease the effect existed in the traditional random coupling model, a short-orbit random coupling model (SORCM) of the two-port wave chaotic cavity is proposed by defining a short-orbit correction coefficient of the radiation impedance.The variation of root-mean-square error of induced voltage at the target point is analyzed with the largest short-orbit length.In different frequency range, the statistical characteristics and calculated results of the SORCM are compared with experimental data which can verify the correctness of the model.Theoretical analysis and experimental results show that the SORCM is more effective compared with the traditional random coupling model.It can be used to predict and analyze electromagnetic pulse effects of the complex electronic equipment.

wave-chaotic cavity;electromagnetic pulse effect;short-orbit random coupling model;radiation impedance

李福林, 韓繼紅, 張暢.二端口波混沌腔體短跡線隨機耦合模型[J].電波科學學報,2016,31(5):912-919.

10.13443/j.cjors.2016070501

LI F L, HAN J H, ZHANG C.Short-orbit random coupling model in two-port wave-chaotic cavity[J].Chinese journal of radio science,2016,31(5):912-919.(in Chinese).DOI：10.13443/j.cjors.2016070501

2016-07-05

國防科研項目

O414.2;O415.5

A

1005-0388(2016)05-0912-08

聯系人：李福林 E-mail：leefulin@163.com