超聲波電動(dòng)機(jī)阻抗特性研究
陳張麒,楊 明,董兆鵬
(上海交通大學(xué),上海 200240)
?
超聲波電動(dòng)機(jī)阻抗特性研究
陳張麒,楊 明,董兆鵬
(上海交通大學(xué),上海 200240)
超聲波電動(dòng)機(jī)的阻抗模型通常為靜態(tài)電容和一個(gè)動(dòng)態(tài)支路并聯(lián),針對(duì)超聲波電動(dòng)機(jī)有多個(gè)諧振區(qū)的特征,提出了復(fù)合動(dòng)態(tài)支路模型。在工作頻帶內(nèi),該模型的阻抗特性曲線能與電機(jī)實(shí)測阻抗特性曲線較好地?cái)M合,經(jīng)過阻抗匹配后的阻抗特性整體上更優(yōu)于單動(dòng)態(tài)支路模型。
超聲波電動(dòng)機(jī);動(dòng)態(tài)支路;阻抗特性;仿真;阻抗匹配
0 引 言
超聲波電動(dòng)機(jī)和功率超聲換能器一樣屬于容性負(fù)載,都是基于壓電材料逆壓電效應(yīng)的電-機(jī)轉(zhuǎn)換元件。換能器所使用壓電材料的結(jié)構(gòu)和工作機(jī)理較簡單,工作頻帶較窄,工作頻率處的諧振區(qū)附近沒有其他明顯的諧振區(qū);而超聲波電動(dòng)機(jī)結(jié)構(gòu)和工作機(jī)理比較特殊,工作頻率處的諧振區(qū)附近往往還有其他明顯的諧振區(qū)。
超聲波電動(dòng)機(jī)的等效電路模型是通過將定、轉(zhuǎn)子的機(jī)械量等效為合適的電量,將定子的質(zhì)量、剛度和阻尼等效為合適的電子元件,從而實(shí)現(xiàn)對(duì)超聲波電動(dòng)機(jī)特性的分析和仿真[1]。通常是將超聲波電動(dòng)機(jī)等效為靜態(tài)電容和一個(gè)動(dòng)態(tài)支路并聯(lián)的結(jié)構(gòu),其中動(dòng)態(tài)支路對(duì)應(yīng)著工作頻率處的諧振區(qū)[2]。目前,在等效電路模型的研究方面,Kanbe等人提出了超聲波電動(dòng)機(jī)Mason電路;Mojallali等人建立了超聲波電動(dòng)機(jī)定子的等效電路模型,其中包含了介電損耗、振動(dòng)損耗和定子質(zhì)量及剛度[3-5]。以上都是研究超聲波電動(dòng)機(jī)在工作頻率處的阻抗特性,不考慮工作頻率附近其他諧振區(qū)對(duì)電機(jī)阻抗變化的影響。為了得到更精確的阻抗特性,考慮使用超聲波電動(dòng)機(jī)的多個(gè)動(dòng)態(tài)支路并聯(lián)的復(fù)合動(dòng)態(tài)支路代替常用的單動(dòng)態(tài)支路。
1 超聲波電動(dòng)機(jī)阻抗模型
1.1 常見的超聲波電動(dòng)機(jī)阻抗模型
超聲波電動(dòng)機(jī)定子在諧振頻率附近的等效阻抗模型如圖1(a)所示,其中C0為壓電振子的靜態(tài)電容,C1,L1和R1分別是動(dòng)態(tài)支路上相應(yīng)的動(dòng)態(tài)電阻、動(dòng)態(tài)電容和動(dòng)態(tài)電感[6]。當(dāng)電機(jī)處于諧振狀態(tài)時(shí),近似滿足:
(1)
式中:wp為諧振頻率所對(duì)應(yīng)的諧振角頻率。此時(shí)串聯(lián)支路中C1和L1的阻抗相互抵消,整體阻抗等效于C0和R1并聯(lián),如圖1(b)所示,此時(shí)負(fù)載呈容性。
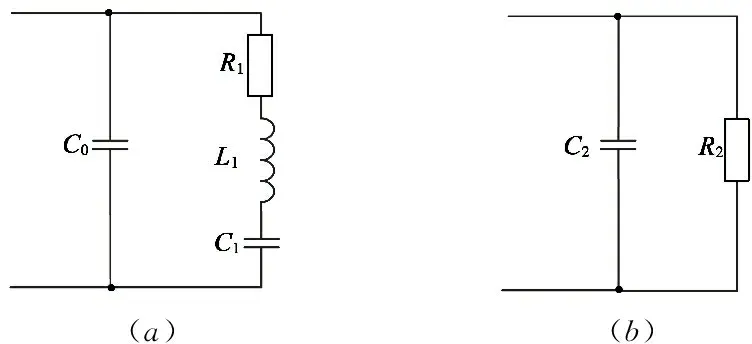
(a)(b)
圖1 壓電振子諧振頻率附近的電路等效圖
1.2 電機(jī)的基本參數(shù)
測試所用的超聲波電動(dòng)機(jī)型號(hào)為TRUM-60-P,阻抗分析儀為北京邦聯(lián)時(shí)代電子科技有限公司生產(chǎn)的PV70A。通過阻抗分析儀測得該超聲波電動(dòng)機(jī)在20~100 kHz內(nèi)有很多組諧振點(diǎn)和反諧振點(diǎn),其中有3個(gè)幅值和相位變化較明顯的區(qū)域在35~60 kHz頻段內(nèi),分別測試該超聲波電動(dòng)機(jī)A相和B相的阻抗特性曲線,如圖2所示。
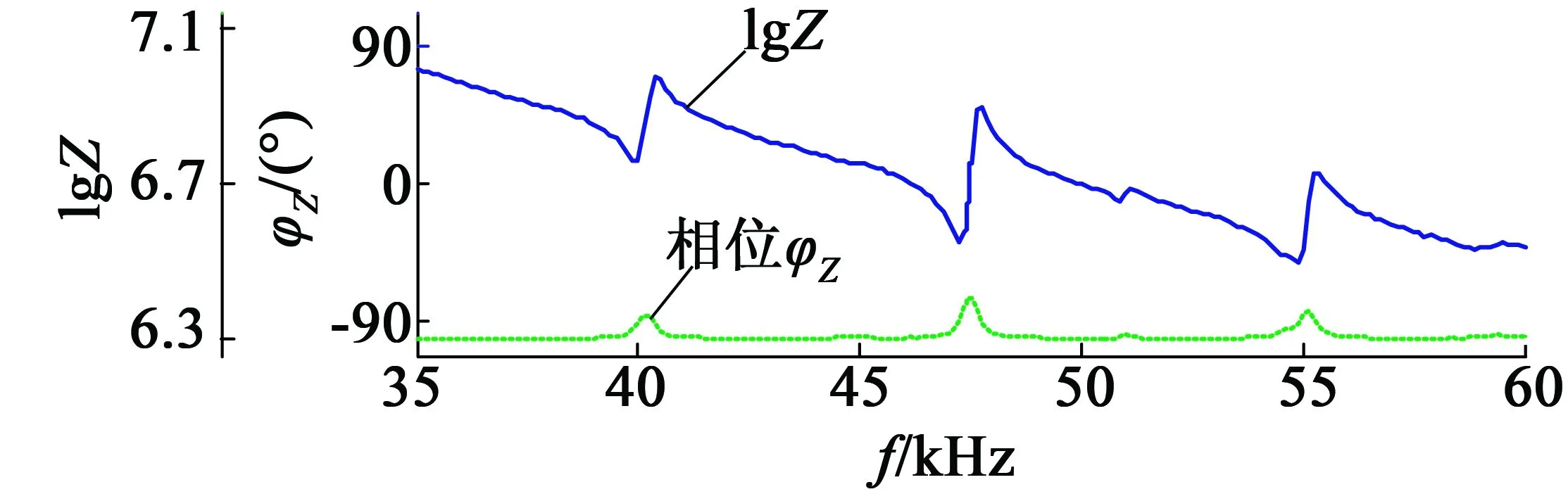
(a) A相阻抗特性
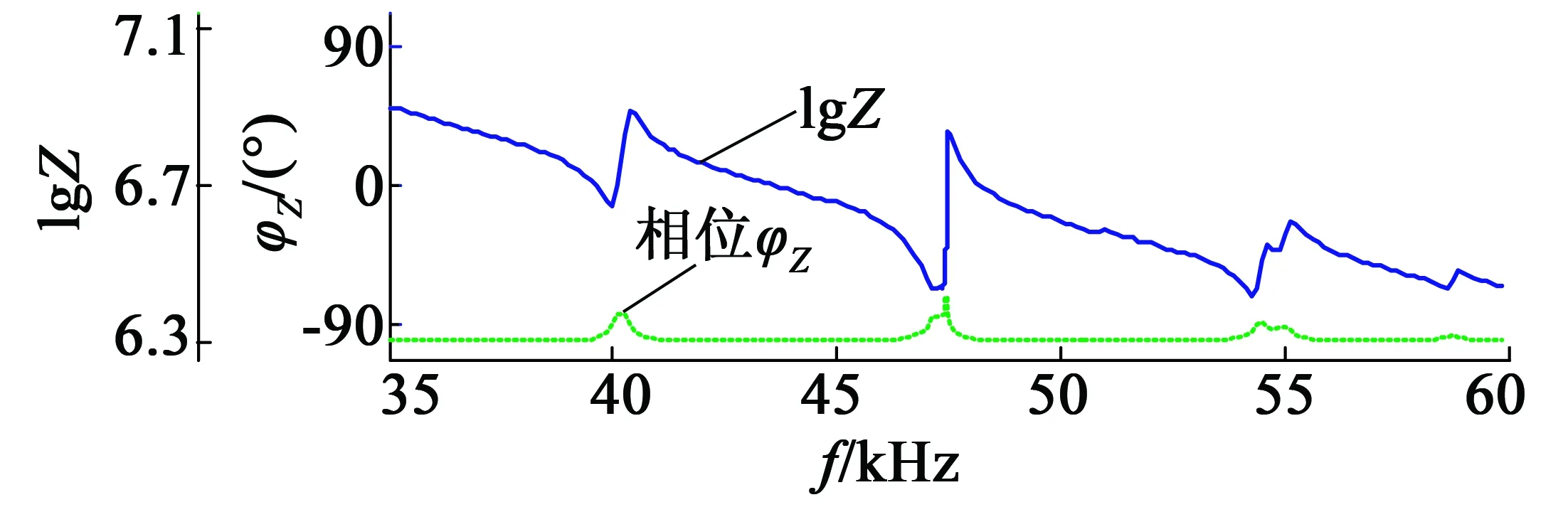
(b) B相阻抗特性
圖2 TRUM-60-P在35~60 kHz頻帶內(nèi)的阻抗特性曲線
上圖中可以看出電機(jī)A相和B相在40 kHz、48 kHz和55 kHz附近分別有一對(duì)諧振點(diǎn)和反諧振點(diǎn),兩者走向基本一致,但不能完全重合,原因是兩相壓電陶瓷的做工不可能完全一致。由于差異不大,因此在匹配參數(shù)的設(shè)計(jì)中,忽略A相、B相的差異,下文均以電機(jī)A相特性作為研究對(duì)象。實(shí)際測試中,用阻抗分析儀測得不同頻帶下的參數(shù)有差異。分別測得37~43 kHz、43~50 kHz和50~58 kHz頻帶下的參數(shù)如表1所示。
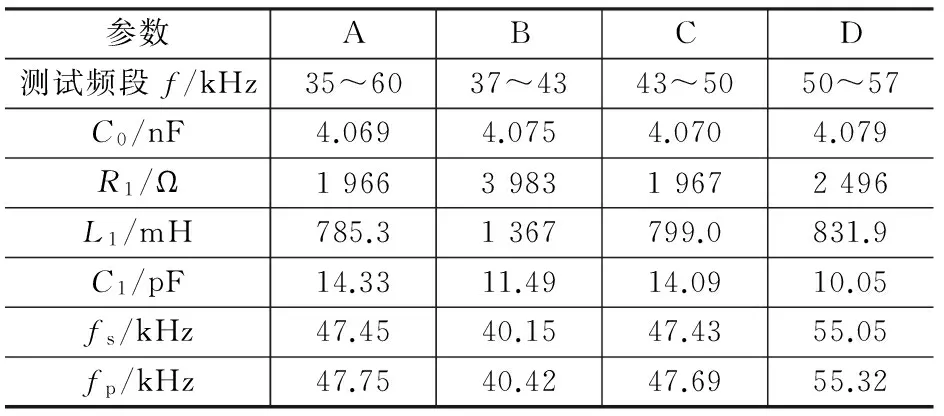
表1 TRUM-60-P電機(jī)測試參數(shù)
表中fs為串聯(lián)諧振頻率,fp為并聯(lián)諧振頻率。分析表中的數(shù)據(jù),超聲波電動(dòng)機(jī)在35~60 kHz頻段與43~50 kHz頻段內(nèi)測得的數(shù)據(jù)非常接近,可以認(rèn)為壓電陶瓷的主諧振區(qū)靠近48 kHz。但是該超聲波電動(dòng)機(jī)的機(jī)械機(jī)構(gòu)等參數(shù)決定了電機(jī)的工作頻帶為40~45 kHz,較好的工作頻率為40.3 kHz,因此重點(diǎn)研究該電機(jī)在測試頻段37~43 kHz內(nèi)所對(duì)應(yīng)的諧振區(qū)的阻抗特性。
1.3 復(fù)合動(dòng)態(tài)支路模型
由于該電機(jī)在35~60 kHz內(nèi)有多個(gè)明顯的諧振區(qū),可以認(rèn)為其動(dòng)態(tài)支路由相應(yīng)的多個(gè)支路并聯(lián)而成,每個(gè)支路的動(dòng)態(tài)電阻、動(dòng)態(tài)電感和動(dòng)態(tài)電容值分別由相應(yīng)的諧振區(qū)來確定,針對(duì)TRUM-60-P建立復(fù)合動(dòng)態(tài)支路的電機(jī)阻抗模型如圖3所示。
Ri,Li,Ci(i=1,2,3)分別對(duì)應(yīng)第i條動(dòng)態(tài)支路上的動(dòng)態(tài)電阻、動(dòng)態(tài)電感和動(dòng)態(tài)電容。上述模型是針對(duì)該電機(jī)在測量頻帶35~60 kHz下得到,如果適
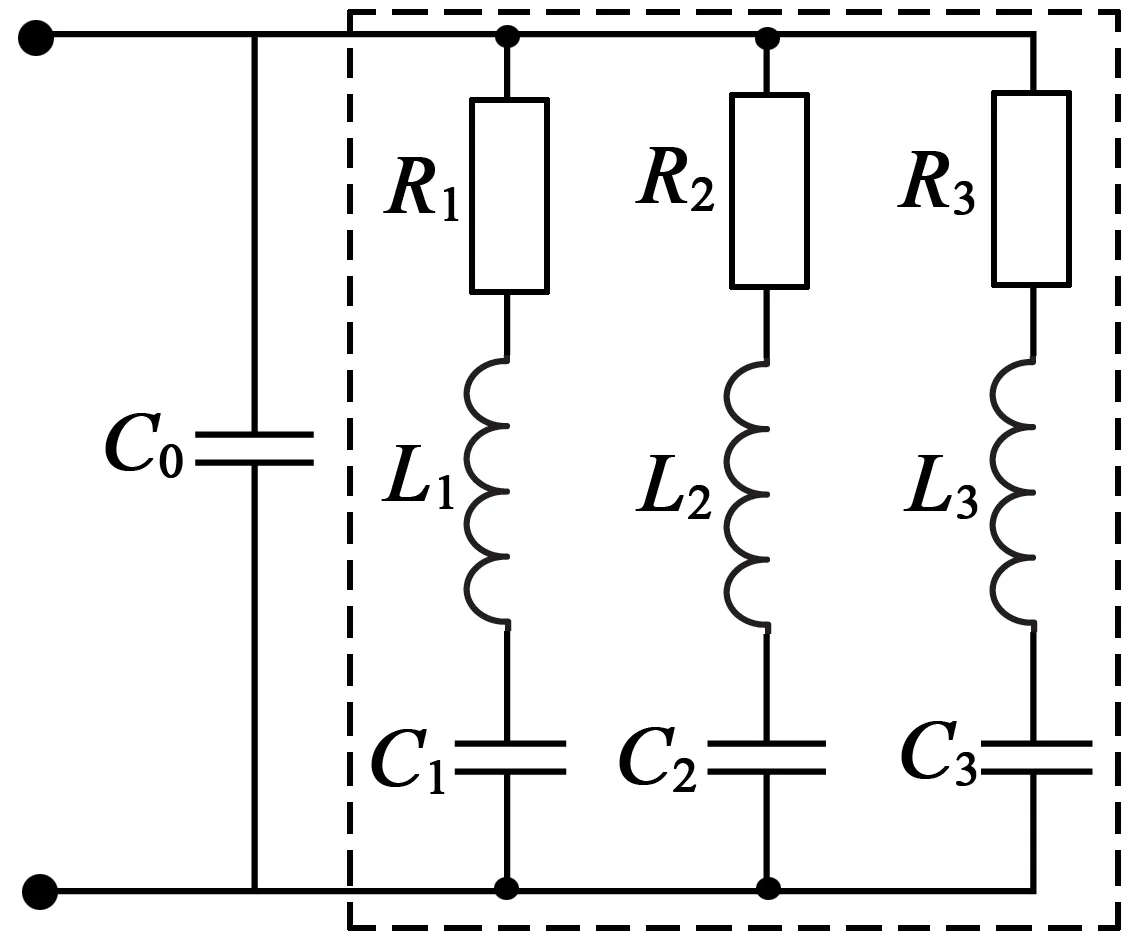
圖3 超聲波電動(dòng)機(jī)復(fù)合動(dòng)態(tài)支路模型
當(dāng)擴(kuò)大測量頻帶,可以得到更多的動(dòng)態(tài)支路,對(duì)于阻抗曲線有n條動(dòng)態(tài)支路的超聲波電動(dòng)機(jī),其單相阻抗表達(dá)式:
(2)
其中:
(3)
理論上,加入的動(dòng)態(tài)支路越多,所得到的總阻抗越接近實(shí)際值,但考慮Zi的數(shù)值受wp影響較大,通常只取工作頻帶附近且阻抗變化較明顯的區(qū)域所對(duì)應(yīng)的動(dòng)態(tài)支路,其余的動(dòng)態(tài)支路可以忽略不計(jì),具體可以根據(jù)阻抗儀得到的阻抗曲線來選取。
2 仿真及測試
2.1 復(fù)合動(dòng)態(tài)支路模型在寬頻帶下的阻抗特性
代入表中數(shù)據(jù),繪制電機(jī)的復(fù)合動(dòng)態(tài)支路模型在35~60 kHz頻帶內(nèi)的阻抗特性曲線如圖4的上圖所示,下圖為同頻帶下用阻抗分析儀實(shí)測的曲線圖,二者數(shù)值大小及走向基本一致,且上圖的曲線比下圖更平滑,說明該阻抗模型能在較寬的頻帶內(nèi)反映出電機(jī)阻抗變化。
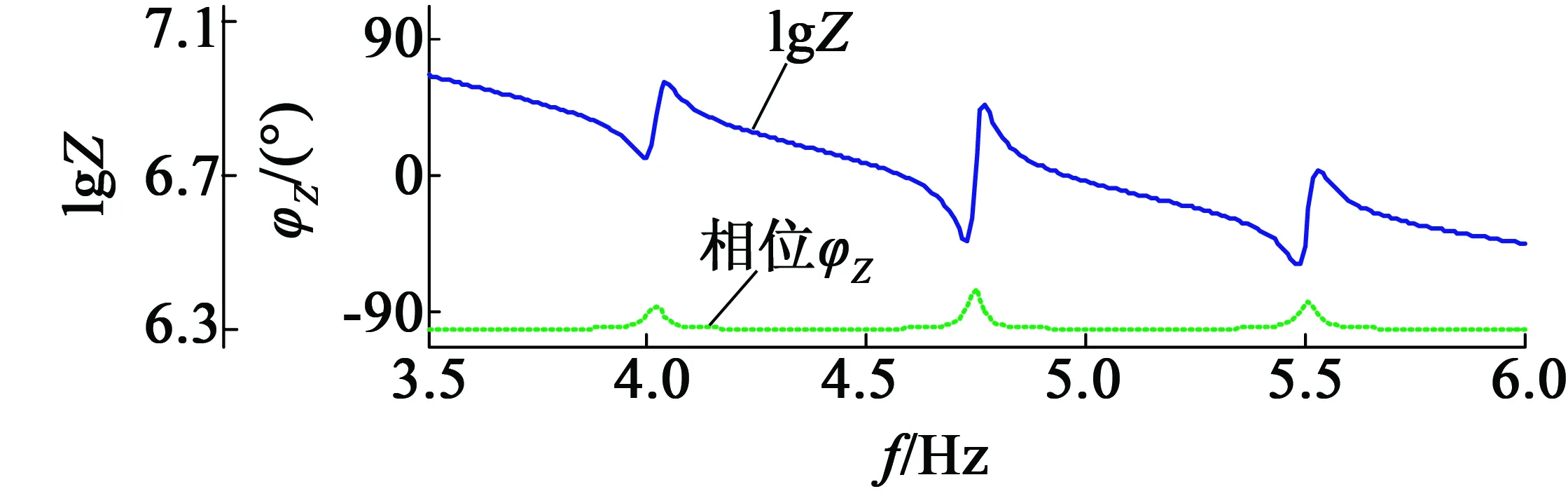
(a) 復(fù)合動(dòng)態(tài)支路模型
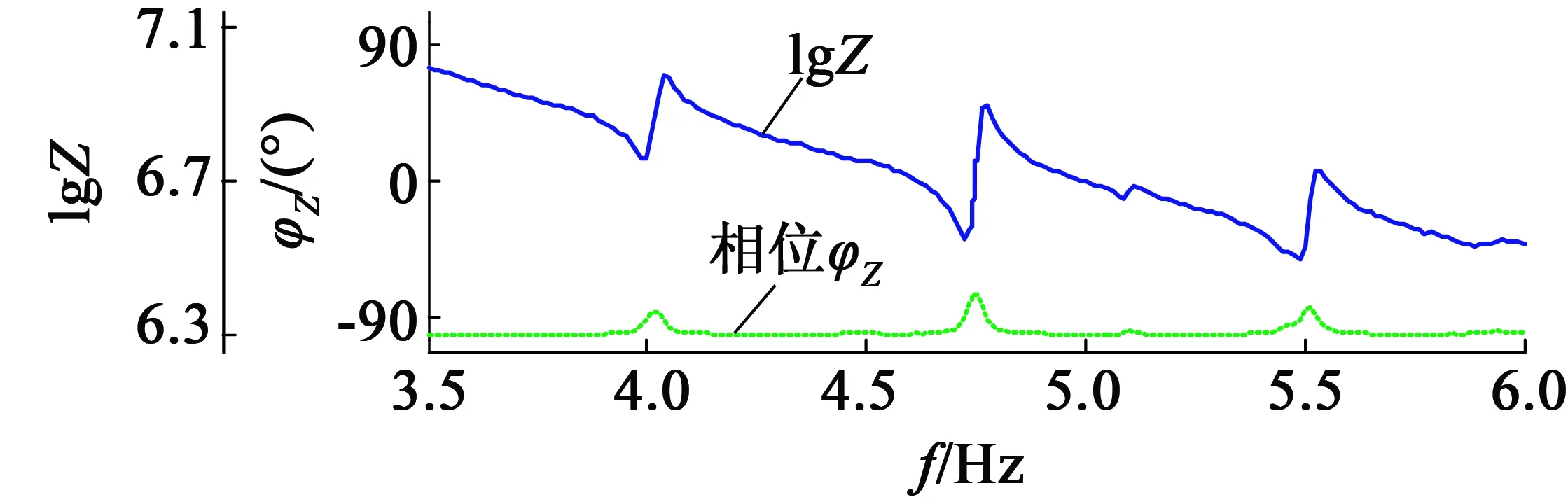
(b) 阻抗儀實(shí)測
圖4 電機(jī)在35~60 kHz頻段內(nèi)的仿真和實(shí)測阻抗曲線圖
2.2 兩種電機(jī)模型阻抗曲線與阻抗儀實(shí)測曲線對(duì)比
由于該電機(jī)的工作頻帶為40~45 kHz,在該頻段下,將單動(dòng)態(tài)支路和復(fù)合動(dòng)態(tài)支路阻抗曲線與阻抗儀實(shí)測曲線進(jìn)行對(duì)比,代入數(shù)據(jù)點(diǎn)計(jì)算均方根值(RMSE)來分析曲線的擬合程度,如圖5所示。單動(dòng)態(tài)支路模型阻抗幅值曲線與實(shí)測曲線的RMSE(lgZ)為19.15,復(fù)合動(dòng)態(tài)支路模型阻抗幅值曲線與實(shí)測曲線的RMSE(lgZ)為9.54,明顯小于前者,而阻抗相位曲線的RMSE(φZ)均較小且比較接近,可以認(rèn)為復(fù)合動(dòng)態(tài)支路電機(jī)模型阻抗特性更接近超聲波電動(dòng)機(jī)的實(shí)際阻抗特性。
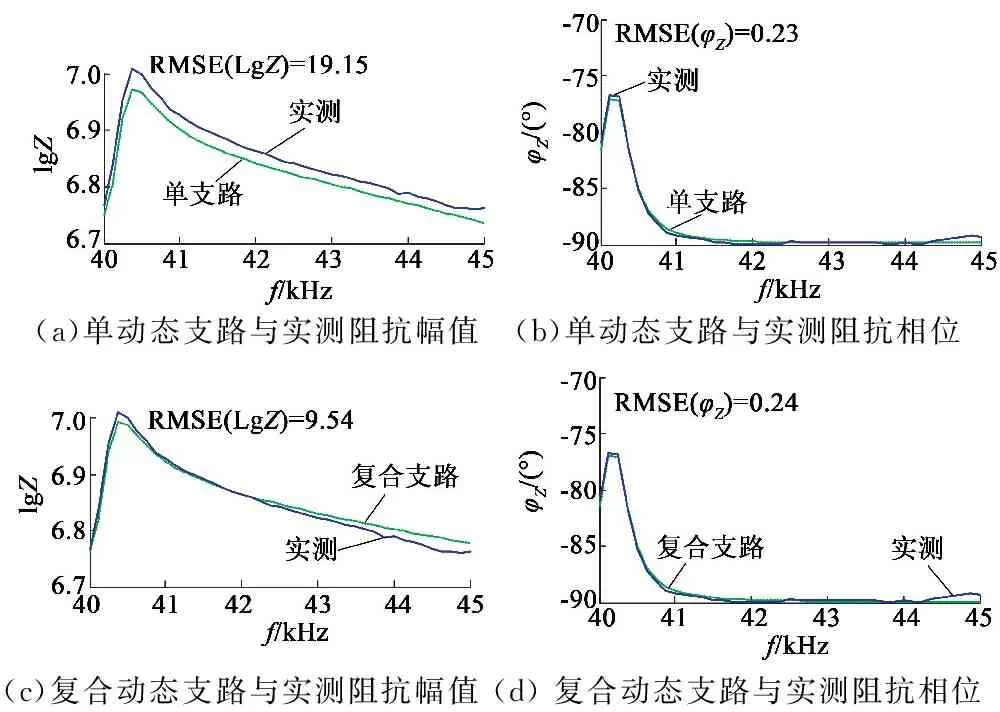
(a)單動(dòng)態(tài)支路與實(shí)測阻抗幅值(b)單動(dòng)態(tài)支路與實(shí)測阻抗相位(c)復(fù)合動(dòng)態(tài)支路與實(shí)測阻抗幅值 (d)復(fù)合動(dòng)態(tài)支路與實(shí)測阻抗相位
圖5 超聲波電動(dòng)機(jī)阻抗特性曲線
2.3 阻抗匹配后超聲波電動(dòng)機(jī)兩種模型的阻抗曲線與阻抗儀實(shí)測曲線對(duì)比
為減小超聲波電機(jī)的無功損耗,提高超聲波電動(dòng)機(jī)驅(qū)動(dòng)電源的效率,必須在超聲波電機(jī)與驅(qū)動(dòng)器之間增加匹配電路,包含變壓器和次級(jí)串聯(lián)匹配電感[7]。將超聲波電動(dòng)機(jī)連接匹配電路的輸出端,如圖6所示,Zl為超聲波電動(dòng)機(jī)的阻抗,Zs為變壓器
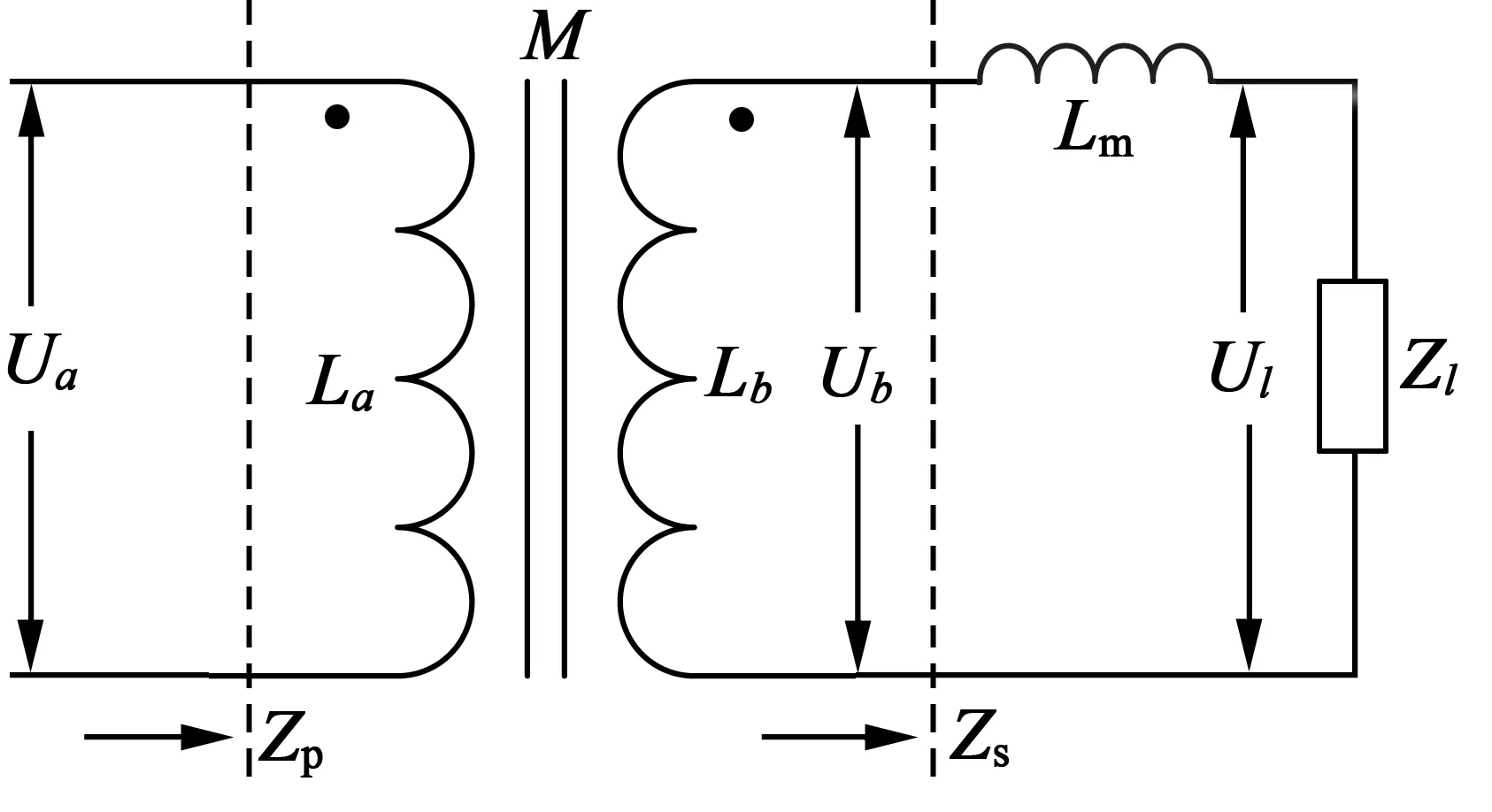
圖6 超聲波電動(dòng)機(jī)阻抗匹配圖
次級(jí)負(fù)載阻抗,Lm為匹配電感的值,M為變壓器互感值[8],Zp為負(fù)載和匹配電路的整體阻抗,可由下式計(jì)算[9-10]:
(4)
匹配元件參數(shù)如表2所示。

表2 匹配元件參數(shù)表
將Zl分別代入單動(dòng)態(tài)支路電機(jī)模型和復(fù)合動(dòng)態(tài)支路電機(jī)模型得到的阻抗,求出Zp并繪制阻抗特性曲線,與匹配板輸入端實(shí)測的阻抗曲線進(jìn)行比較,如圖7所示。
在40~45 kHz頻帶內(nèi),匹配后的復(fù)合動(dòng)態(tài)支路電機(jī)模型的阻抗幅值特性明顯比單動(dòng)態(tài)支路模型更接近實(shí)測曲線,但是在相位特性上略遜于單動(dòng)態(tài)支路模型,且二者比較接近,與圖5中的阻抗特性的對(duì)比結(jié)果很相似。可以認(rèn)為,復(fù)合動(dòng)態(tài)支路電機(jī)模型整體上要優(yōu)于傳統(tǒng)的單動(dòng)態(tài)支路電機(jī)模型。
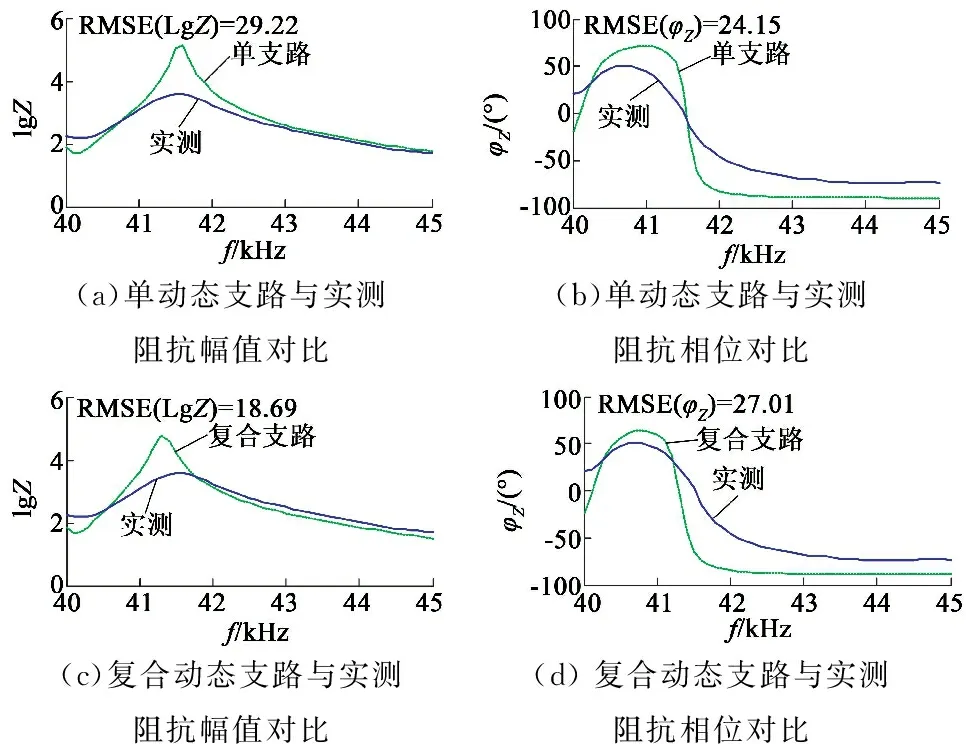
(a)單動(dòng)態(tài)支路與實(shí)測阻抗幅值對(duì)比(b)單動(dòng)態(tài)支路與實(shí)測阻抗相位對(duì)比(c)復(fù)合動(dòng)態(tài)支路與實(shí)測阻抗幅值對(duì)比(d)復(fù)合動(dòng)態(tài)支路與實(shí)測阻抗相位對(duì)比
圖7 超聲波電動(dòng)機(jī)阻抗匹配后的阻抗特性曲線
3 結(jié) 語
復(fù)合動(dòng)態(tài)支路模型比傳統(tǒng)的單動(dòng)態(tài)支路模型得到的阻抗特性更接近超聲波電動(dòng)機(jī)的實(shí)際情況,該模型可用于阻抗匹配的參數(shù)優(yōu)化等應(yīng)用場合,其中更詳細(xì)的機(jī)理機(jī)制有待后續(xù)研究。
[1] 袁志兵. 基于PSoC的超聲波電動(dòng)機(jī)驅(qū)動(dòng)電源的研究[D]. 南京:南京航空航天大學(xué),2010.
[2] NESBITT W H,ANDREW J M.Modeling of a piezoelectric rotary ultrasonic motor [J].IEEE Trans. Ultrason. Ferroelec. Freq. Contr.,1995,42(2):210224.
[3] KANBE N,AOYAGI M,HIROSE S,et al.Impedance-type equivalent circuits of the piezoelectric vibrator for applications to ultrasonic motors and actuators[J].Journal of the Acoustical Society of Japan,1993,14(4):235-242.
[4] MOJALLALI H,AMINI R,IZADI-ZAMANABADI R,et al.Free stator modeling of a traveling wave ultrasonic motor[C]//Proceedings of the 2005 IEEE International Symposium on Mediterrean Conference on Control and Automation Intelligent Control,Cyprus.IEEE,2005:1068-1073.
[5] 顏佳佳,阮新波.旋轉(zhuǎn)型行波超聲波電動(dòng)機(jī)的等效電路模型[J].中國電機(jī)工程學(xué)報(bào).2009,29(15):80-87.
[6] 潘仲明,祝琴. 壓電換能器阻抗匹配技術(shù)研究[J].應(yīng)用聲學(xué).2007,26(6):357-361.
[7] 袁義坤,趙增輝,王育平,等.超聲波電動(dòng)機(jī)定子等效電路模型及驅(qū)動(dòng)電路的阻抗匹配[J].微特電機(jī).2012,40(2):62-64.
[8] 王素姣.磁耦合線圈互感系數(shù)M的測量[J].鄭州鐵路職業(yè)技術(shù)學(xué)院學(xué)報(bào). 2002,14(2):43-44.
[9] 李柄毅.超聲波電源功率控制的研究[D].洛陽:河南科技大學(xué),2013.
[10] 武劍,董惠娟,張松柏,等.壓電超聲換能器初級(jí)串聯(lián)匹配新方法[J]. 吉林大學(xué)學(xué)報(bào)(工學(xué)版),2009,39(6):1641-1645.
The Research of Impedance Characteristic for Ultrasonic Motor
CHENZhang-qi,YANGMing,DONGZhao-peng
(Shanghai Jiao Tong University,Shanghai 200240,China)
The impedance model of ultrasonic motor usually contains a static capacitance and a dynamic branch in parallel, while the complex dynamic branch model is put forward based on the characteristic of ultrasonic motor that has multiple resonance areas. The resonance characteristic curve of this model fitted well with the curve that was actual measured in the working frequency, and also closer to the actual characteristic than single dynamic branch model after impedance matching.
ultrasonic motor; dynamic branch; impedance characteristic; simulation; impedance matching
2015-09-22
國家自然科學(xué)基金項(xiàng)目(51275287)
TM359.9
A
1004-7018(2016)07-0001-03
陳張麒(1992-)男,碩士研究生,研究方向?yàn)槌暡妱?dòng)機(jī)驅(qū)動(dòng)控制系統(tǒng)。

