基于MRAS的永磁同步電動機無位置傳感器控制
鄧 鵬
(荊楚理工學(xué)院,荊門 448000)
?
基于MRAS的永磁同步電動機無位置傳感器控制
鄧 鵬
(荊楚理工學(xué)院,荊門 448000)
為了實現(xiàn)永磁同步電動機(PMSM)無位置傳感器控制,提出了一種基于永磁同步電動機兩相靜止α-β坐標(biāo)系下PMSM數(shù)學(xué)模型的模型參考自適應(yīng)(MRAS)位置估算算法。該算法利用α-β坐標(biāo)系下的α軸和β軸電壓、電流及其偏差,借助Lyapunov穩(wěn)定性理論建立了PMSM位置估算模型,并根據(jù)該理論推導(dǎo)出位置參數(shù)的自適應(yīng)率,保證了位置估算模型的穩(wěn)定性和誤差的收斂,同時快速有效地估算出了轉(zhuǎn)子位置。仿真和實驗結(jié)果證明了該位置估算算法的可靠性和有效性。
永磁同步電動機;模型參考自適應(yīng);位置估算
0 引 言
由于永磁同步電動機(以下簡稱PMSM)具有高功率密度、高效率、結(jié)構(gòu)簡單等特點,在驅(qū)動控制領(lǐng)域受到了普遍的關(guān)注。在PMSM的驅(qū)動控制系統(tǒng)中需要精確的轉(zhuǎn)子位置來實現(xiàn)磁場定向,需要轉(zhuǎn)子速度信息實現(xiàn)閉環(huán)控制,這就需要在電機軸上安裝光電編碼器、旋轉(zhuǎn)變壓器等位置傳感器,但是,安裝位置傳感器不僅增加了系統(tǒng)的成本,系統(tǒng)體積也有所增加,并且傳感器的安裝和維護困難,限制了PMSM在相對惡劣環(huán)境條件下的應(yīng)用。因此,永磁同步電動機無位置傳感器控制的重要性日益凸顯。目前,以觀測器為基礎(chǔ)的估算方法,利用電機凸極效應(yīng)的高頻注入法,擴展卡爾曼濾波法都屬于觀測器方法的范疇[1-2],并得到了廣泛的研究,但這些方法算法較為復(fù)雜,算法中的一些參數(shù)的設(shè)置影響其估算性能;高頻注入法雖不依賴于電機的模型,但高頻信號地注入會帶來高頻的噪聲干擾,從而影響系統(tǒng)的性能[3]。綜合上述情況,模型參考自適應(yīng)算法由于是根據(jù)穩(wěn)定性理論來設(shè)計參考系統(tǒng),保證了系統(tǒng)的穩(wěn)定型和魯棒性,因此得到了廣泛的應(yīng)用。
模型參考自適應(yīng)算法(以下簡稱MRAS)的要點主要為收斂算法的設(shè)計,首先,收斂算法需要保證待估模型與參考模型之間的輸出誤差能夠收斂到零[4-8];其次,為了實現(xiàn)轉(zhuǎn)速位置實時計算,必須使得待估模型中估算的轉(zhuǎn)子位置能夠逼近實際位置。目前學(xué)術(shù)界比較常用的收斂算法主要有:局部參數(shù)最優(yōu)化方法,基于Popov穩(wěn)定理論的收斂算法設(shè)計,基于Lyapunov穩(wěn)定性理論的收斂算法設(shè)計。
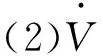
當(dāng)確定的Lyapunov函數(shù)正定時,依據(jù)第(2)條件即可推導(dǎo)出轉(zhuǎn)子位置的收斂率。本文將在PMSM的α-β坐標(biāo)系下利用Lyapunov穩(wěn)定性理論來設(shè)計待估模型中轉(zhuǎn)子位置的自適應(yīng)率。利用Lyapunov穩(wěn)定性理論設(shè)計轉(zhuǎn)子位置估算系統(tǒng)的主要過程如下:(1)對設(shè)定的MRAS位置估算系統(tǒng),推導(dǎo)出轉(zhuǎn)子位置誤差方程;(2)確定一個正定函數(shù)V(x)作為Lyapunov函數(shù);(3)對于V(x),求出Lyapunov函數(shù)沿轉(zhuǎn)子位置誤差方向上的導(dǎo)數(shù);(4)假設(shè)該導(dǎo)數(shù)為負定函數(shù),建立等式,計算出轉(zhuǎn)子位置收斂率。
本文在PMSM的α-β坐標(biāo)系下,根據(jù)MRAS計算出的轉(zhuǎn)子位置收斂率對PMSM轉(zhuǎn)子位置進行估算,以李亞甫洛夫穩(wěn)定性理論為基礎(chǔ),根據(jù)待估模型與參考模型二者之間的誤差建立了轉(zhuǎn)子位置計算模型,并推導(dǎo)出了轉(zhuǎn)子位置的自適應(yīng)率,保證了在一定條件下位置參考系統(tǒng)的穩(wěn)定性和參數(shù)的收斂性。最后通過仿真驗證了該方法的有效性和可靠性。
1 矢量控制下的PMSM位置估算
1.1PMSM數(shù)學(xué)模型的建立
在PMSM數(shù)學(xué)模型的推導(dǎo)中通常需要作以下設(shè)定[9-10]:(1)不考慮鐵心磁路飽和; (2)忽略磁滯損耗和渦流損耗;(3)不考慮轉(zhuǎn)子上的阻尼繞組和永磁體的阻尼作用;(4)反電動勢為正弦。
1.2PMSM位置估算系統(tǒng)
PMSM在兩相α-β靜止坐標(biāo)系下的數(shù)學(xué)模型:
(1)
式中:iα,iβ為定子α,β軸電流;uα,uβ為定子α,β軸電壓;eα,eβ為永磁體反電動勢α,β軸分量;Rs,Ls為定子電阻、dq軸等效電感;ψf為永磁體磁鏈;ωr為轉(zhuǎn)子相角速度;θ為轉(zhuǎn)子位置。
由反電勢的表達式可以看出:反電動勢中含有PMSM轉(zhuǎn)子位置參數(shù)和轉(zhuǎn)速參數(shù)。因此,利用MRAS算法估算出PMSM反電動勢就能進一步計算轉(zhuǎn)子位置和轉(zhuǎn)速。
根據(jù)PMSM矢量控制原理,可得矢量控制下PMSM的MRAS位置估算系統(tǒng)結(jié)構(gòu)圖,如圖1所示。
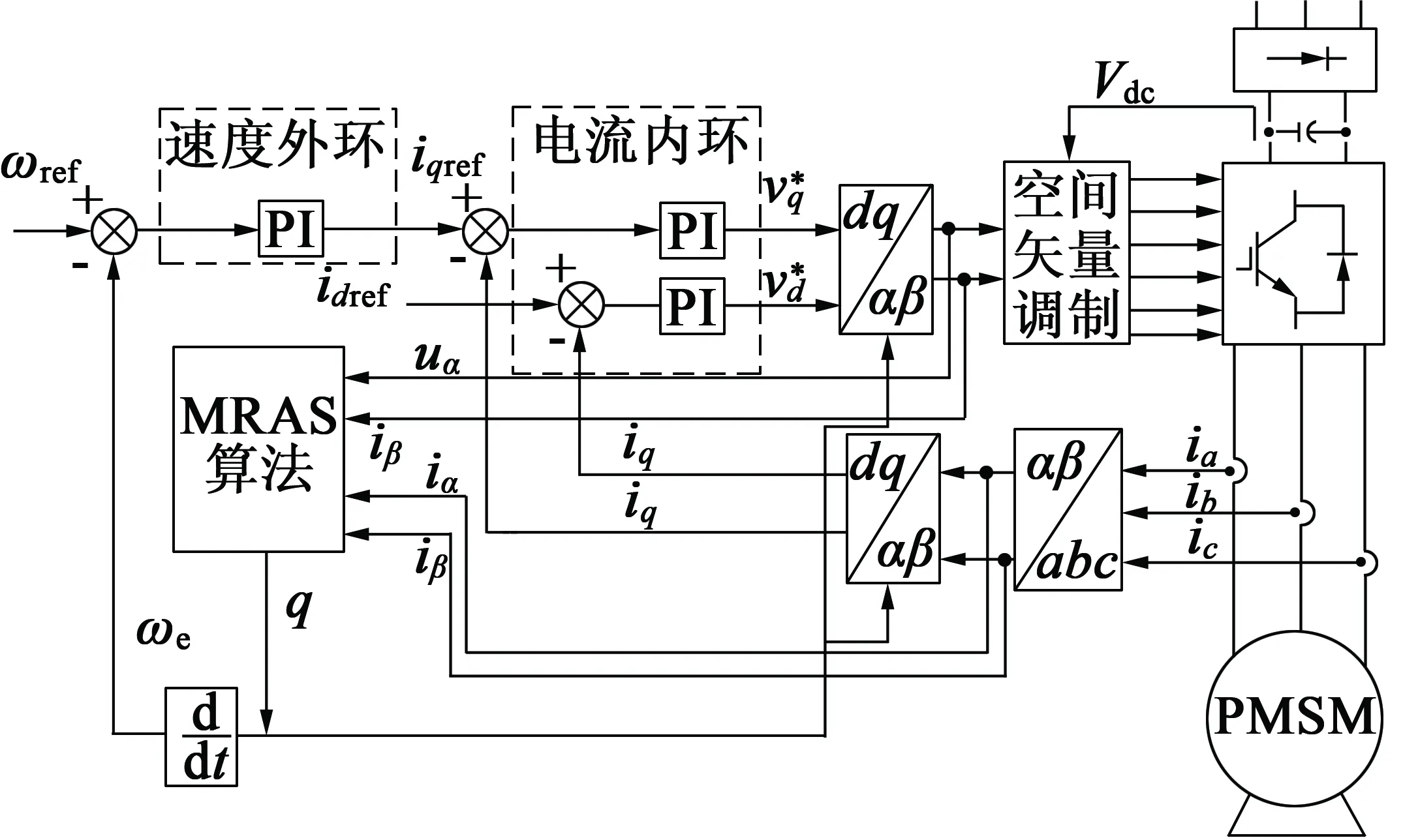
圖1 矢量控制下PMSM的MRAS位置估算系統(tǒng)結(jié)構(gòu)圖
根據(jù)id=0控制,驅(qū)動系統(tǒng)為雙閉環(huán)架構(gòu),控制器采用典型的PI控制。圖2給出了轉(zhuǎn)速位置系統(tǒng)結(jié)構(gòu)圖,該位置估算系統(tǒng)僅需要α,β軸電壓和電流作為輸入信號,這些參數(shù)可通過電流電壓傳感器測得后經(jīng)過坐標(biāo)變換獲得,有利于算法在實際系統(tǒng)下應(yīng)用。
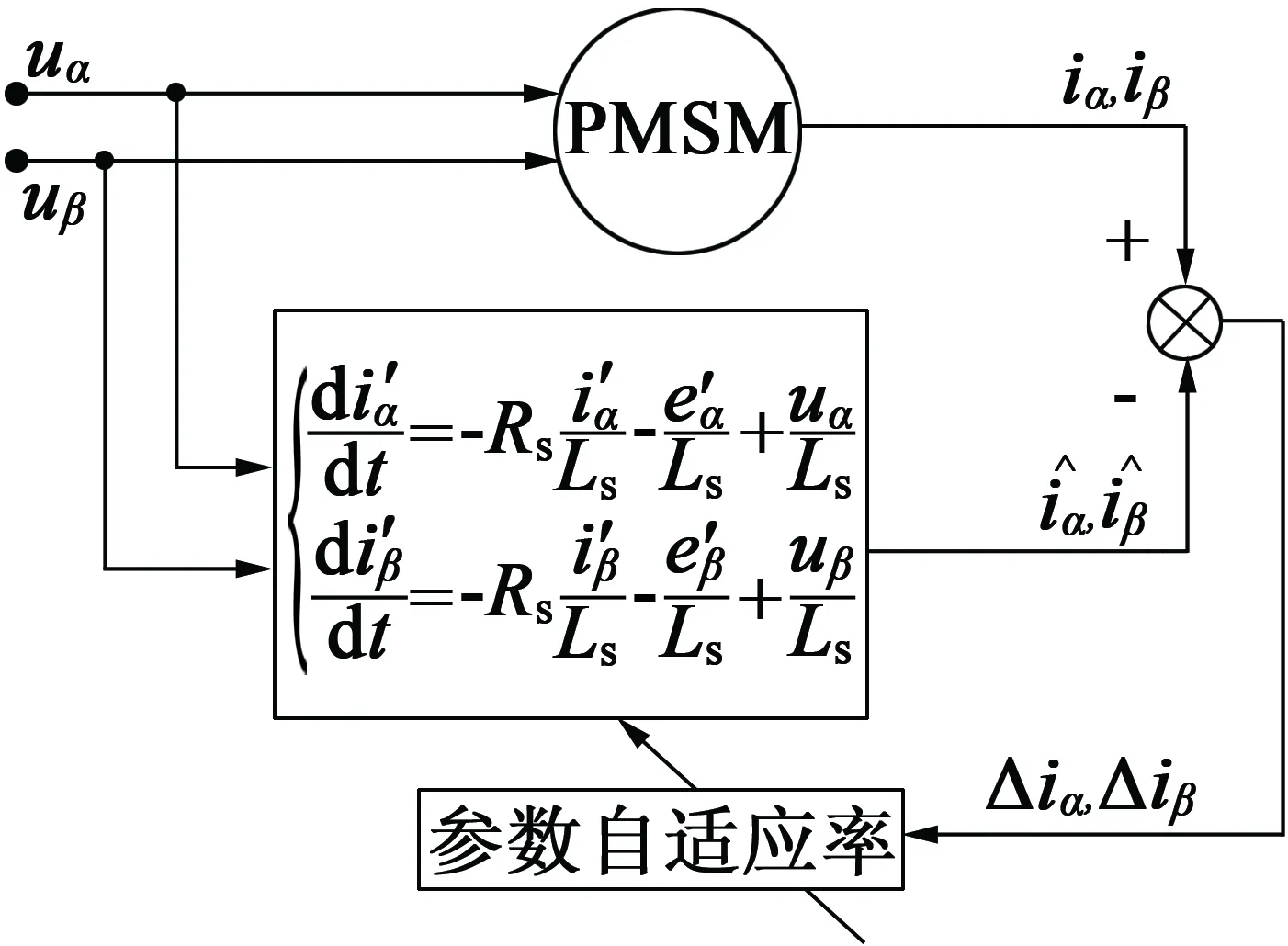
圖2 MRAS轉(zhuǎn)速位置系統(tǒng)結(jié)構(gòu)圖
2 PMSM模型參考自適應(yīng)位置估算
2.1 位置估算模型的構(gòu)建
MRAS算法是基于穩(wěn)定性理論為前提條件來推導(dǎo)出待估參數(shù)收斂的算法,能夠確保整個位置估算系統(tǒng)的穩(wěn)定性,常用的自適應(yīng)控制方法有[11-13]:MIT規(guī)則、Lyapunov穩(wěn)定性判據(jù)和Popov穩(wěn)定性判據(jù)。Lyapunov穩(wěn)定性判據(jù)和Popov穩(wěn)定性判據(jù)都是基于穩(wěn)定性理論進行設(shè)計,對算法的收斂性有所保證,故應(yīng)用廣泛。
在估算轉(zhuǎn)子位置過程當(dāng)中,將PMSM的電壓電流輸出作為參考模型,將含有電機位置參數(shù)的PMSM數(shù)學(xué)模型看作待估模型,兩模型之間的輸入和輸出可通過電壓電流傳感器測得。由兩模型的輸出誤差和計算出的收斂算法來對電機位置進行估算,最終使得估算位置逼近到實際值。
本文利用實際的PMSM作為參考模型,將含有待估位置量的α-β坐標(biāo)系下的PMSM的電壓電流輸出作為待估模型,形成無位置傳感器估算結(jié)構(gòu),其估算系統(tǒng)結(jié)構(gòu)如圖2所示。
2.2 估算自適應(yīng)率推導(dǎo)
由式(1)可得,MRAS待估模型電流模型如下式[14-18]:
(2)
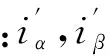
若設(shè):
(3)
則用式(1)減去式(2)后可得:
(4)
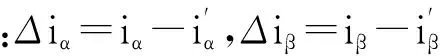
若:
(5)
則式(4)可寫成如下形式:
(6)
選取Lyapunov函數(shù)為如下形式:
(7)
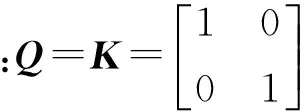
由式(1)可知,反電動勢信號中包含著電機轉(zhuǎn)子的速度和位置信息,故而估算出反電勢即可得出轉(zhuǎn)子位置信息和轉(zhuǎn)速根據(jù)電機反電勢與轉(zhuǎn)子位置的關(guān)系得出估算的位置信號:
若要使轉(zhuǎn)子位置保持收斂,應(yīng)具備前述Lyapunov穩(wěn)定性理論的3個收斂條件
由式(7)可以看出,條件(1)和條件(3)已經(jīng)滿足了。僅對條件(2),根據(jù)式(5)、式(6),可得:
(8)
(9)
(10)
將式(8)、式(9)代入式(10)后,計算可得:
(11)
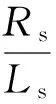
(12)
由于式(11)為負定矩陣,則eT(ATQ+QA)e一定為負定函數(shù),此時若使:
(13)
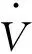
(14)
由式(14)可得反電勢參數(shù)的α-β坐標(biāo)系下自適應(yīng)率分別:
(15)
(16)
Lyapunov穩(wěn)定性理論保證了上述的參數(shù)電流待估模型以及推導(dǎo)的位置參數(shù)收斂算法穩(wěn)定收斂。待估模型中位置量不斷逼近PMSM轉(zhuǎn)子位置,當(dāng)位置估算系統(tǒng)穩(wěn)定時,估算的轉(zhuǎn)子位置即反映了電機的實際轉(zhuǎn)子位置。
3 仿真驗證
為了驗證所提出MRAS位置估算算法的有效性,選用一臺2 kW的永磁同步電動機,額定轉(zhuǎn)速60 r/min,額定轉(zhuǎn)矩300 N·m,極對數(shù)12,相電阻1.8 Ω,相電感12 mH,永磁體磁鏈0.65 Wb。仿真系統(tǒng)按照圖1所示的矢量控制系統(tǒng)框圖搭建。
圖3為電機運行在30 r/min,負載轉(zhuǎn)矩80 N·m下獲得的波形。
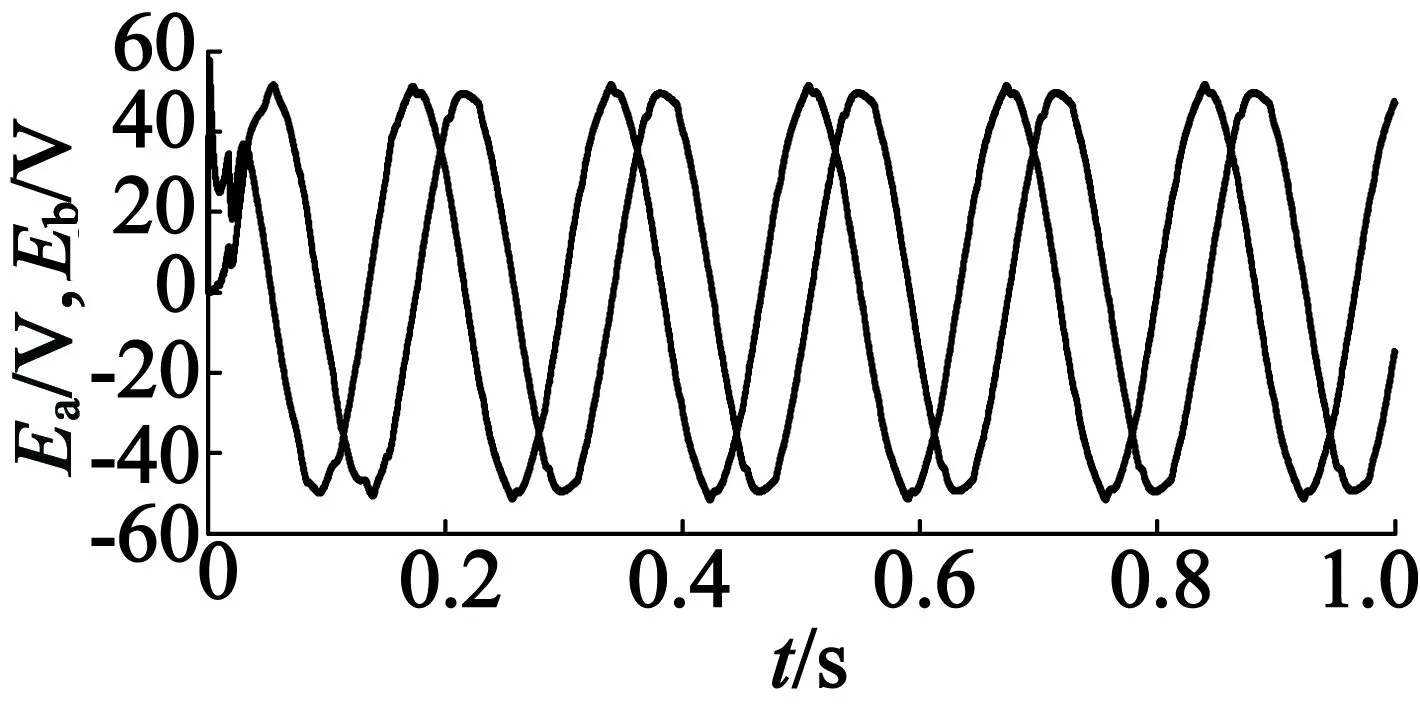
(a) 估算反電動勢波形
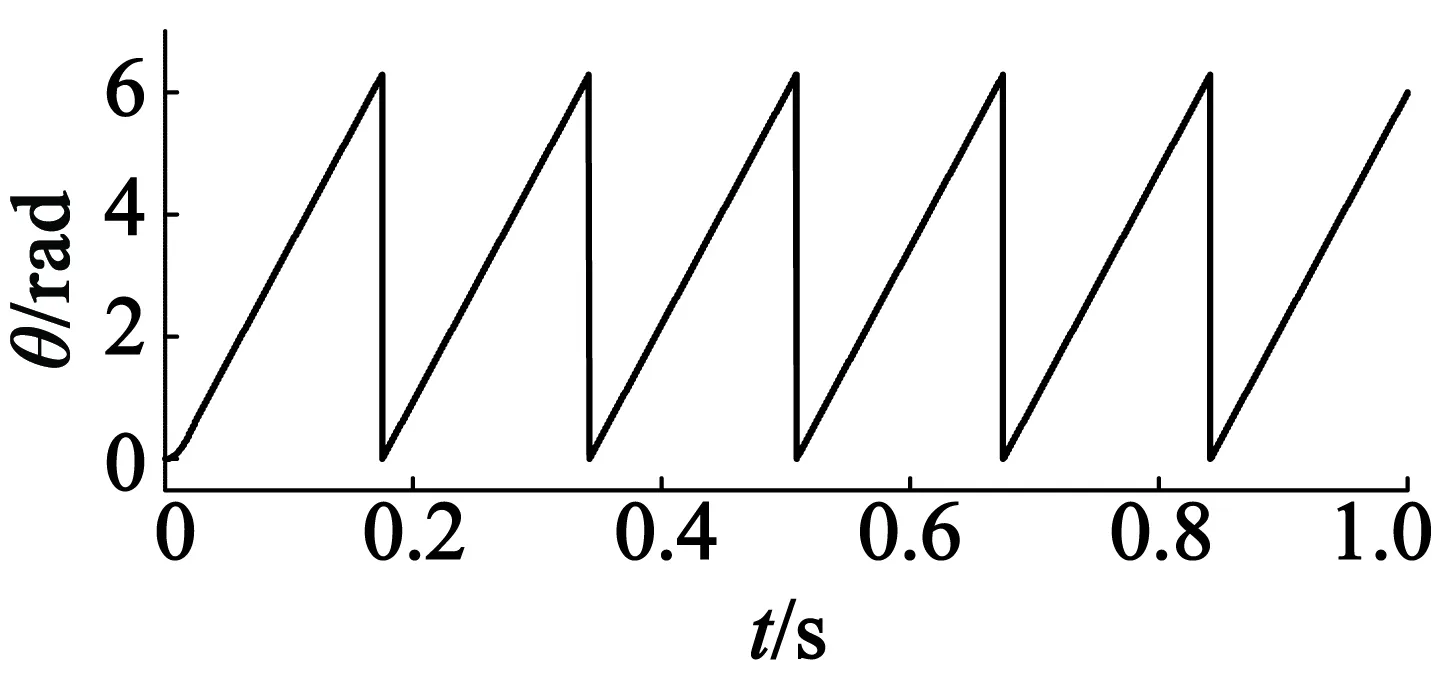
(b) 電機實際位置波形
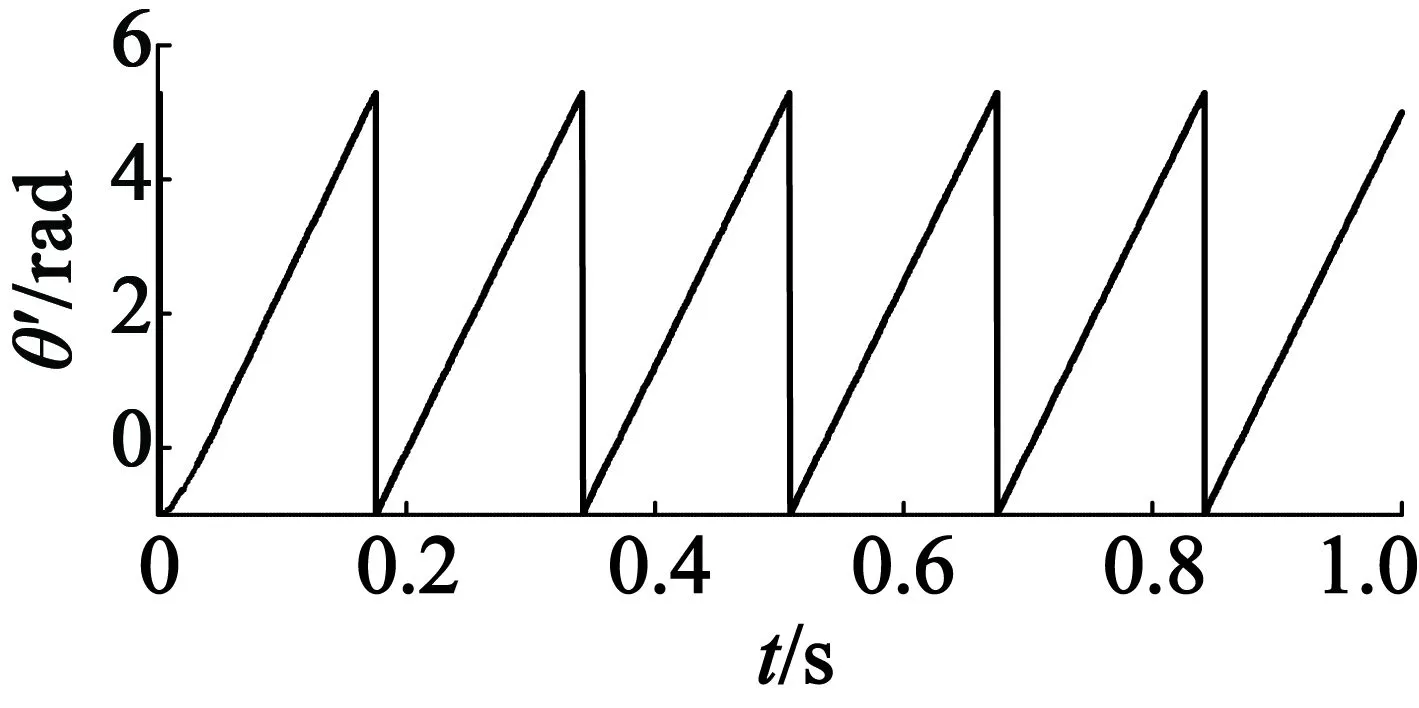
(c) 電機估算位置波形
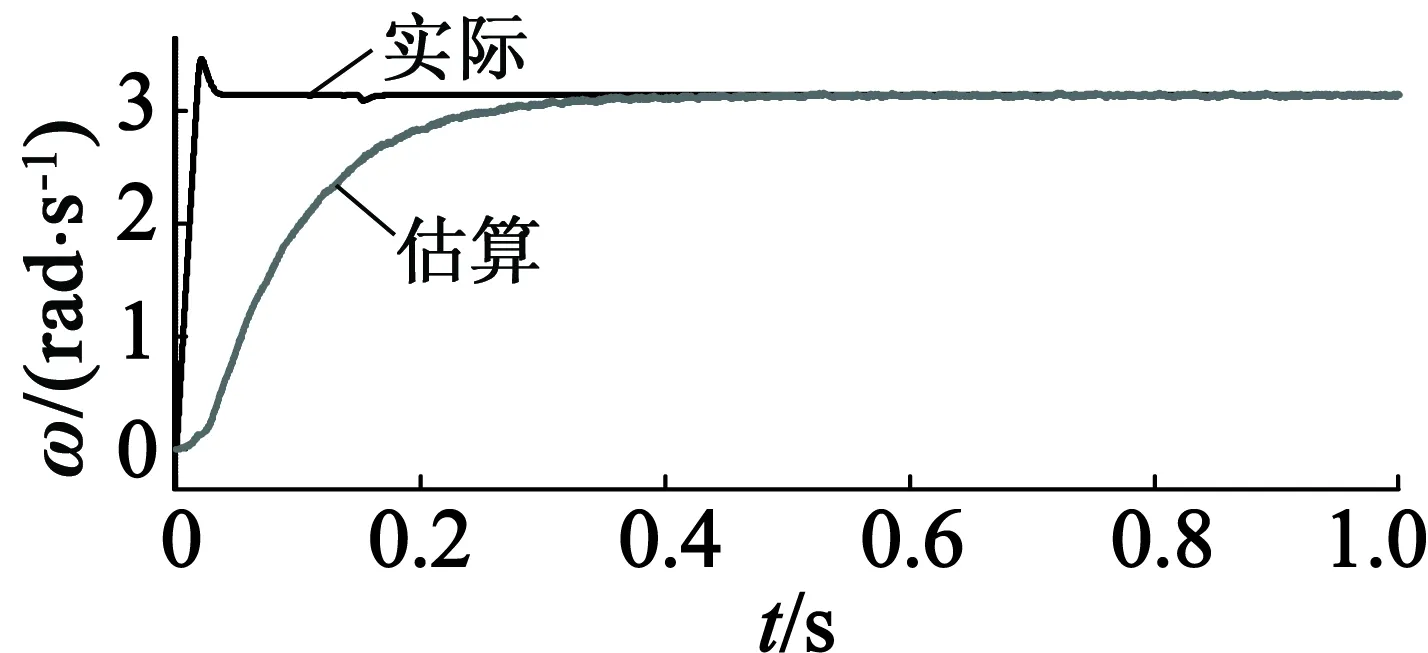
(d) 電機實際轉(zhuǎn)速波形和估算轉(zhuǎn)速波形圖3 轉(zhuǎn)速30 r/min,負載80 N·m的運行波形
由圖3可以看出,在沒有低通濾波器的情況下,使用模型參考自適應(yīng)算法跟蹤兩相靜止坐標(biāo)系下的反電勢波形的方法,得到了理想的反電勢估算波形,估算的位置信號能夠很好地跟蹤實際位置信號,轉(zhuǎn)速估算信號需要0.35 s才能夠跟蹤實際轉(zhuǎn)速,這并不會影響系統(tǒng)的穩(wěn)定運行。
為了進一步驗證本文所提出的位置估算算法的性能,在0.5 s時,給定轉(zhuǎn)速由30 r/min切換到60 r/min,負載轉(zhuǎn)矩為80 N·m,仿真波形如圖4所示。在50 r/min穩(wěn)態(tài)運行時,在0.5 s時刻負載由0突加到300 N·m,仿真波形如圖5所示。
由圖4可以看出,MRAS算法在轉(zhuǎn)速階突變時能夠?qū)D(zhuǎn)子位置準(zhǔn)確估算,轉(zhuǎn)速也可以較快地跟蹤到突變后的轉(zhuǎn)速。
由圖5可以看出,當(dāng)電機負載突變時,位置估算所受影響較小,轉(zhuǎn)速波形在負載突變時短時間內(nèi)與實際轉(zhuǎn)速變化趨勢相反,但是最終都能收斂到實際值。上述的仿真驗證表明,本文提出的MRAS算法在系統(tǒng)穩(wěn)定前提下能夠快速地跟蹤轉(zhuǎn)子位置和轉(zhuǎn)子速度,當(dāng)轉(zhuǎn)速突變和負載突變時仍可保持快速跟蹤性能。
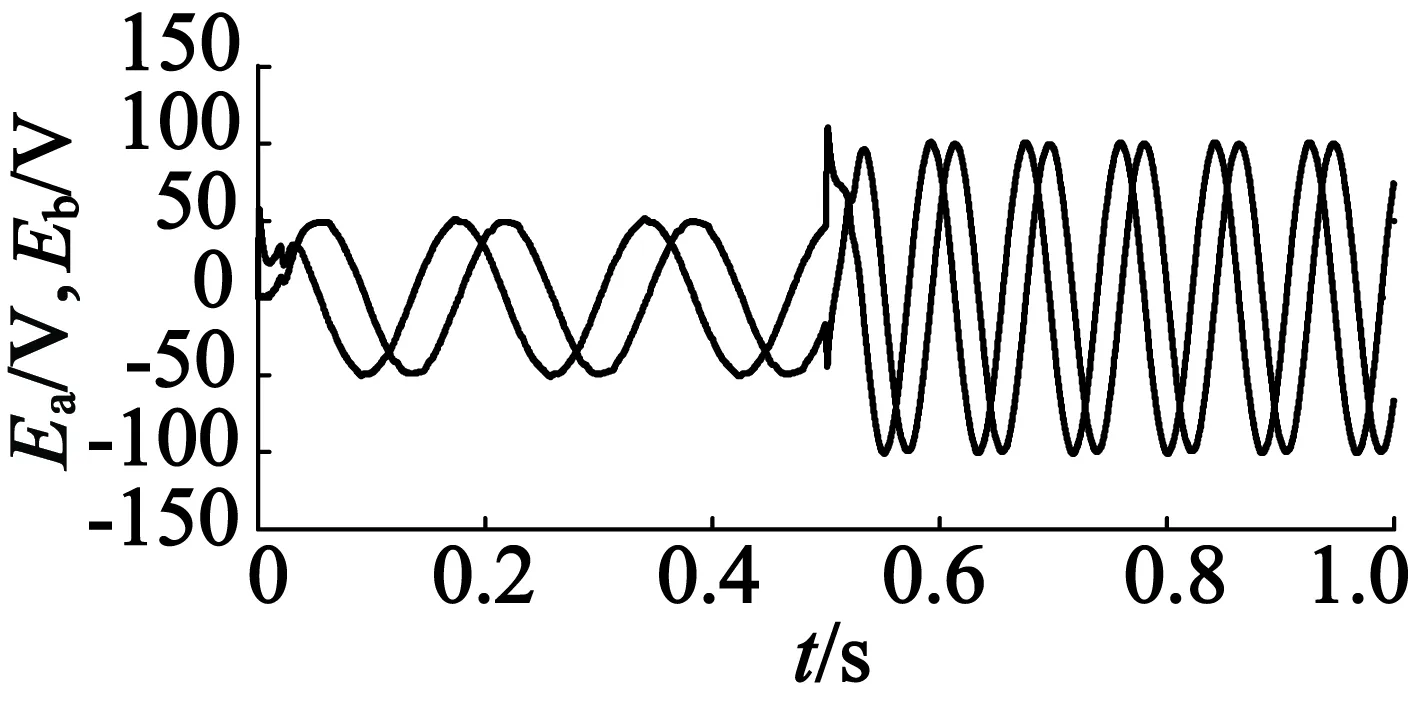
(a) 反電動勢估算波形
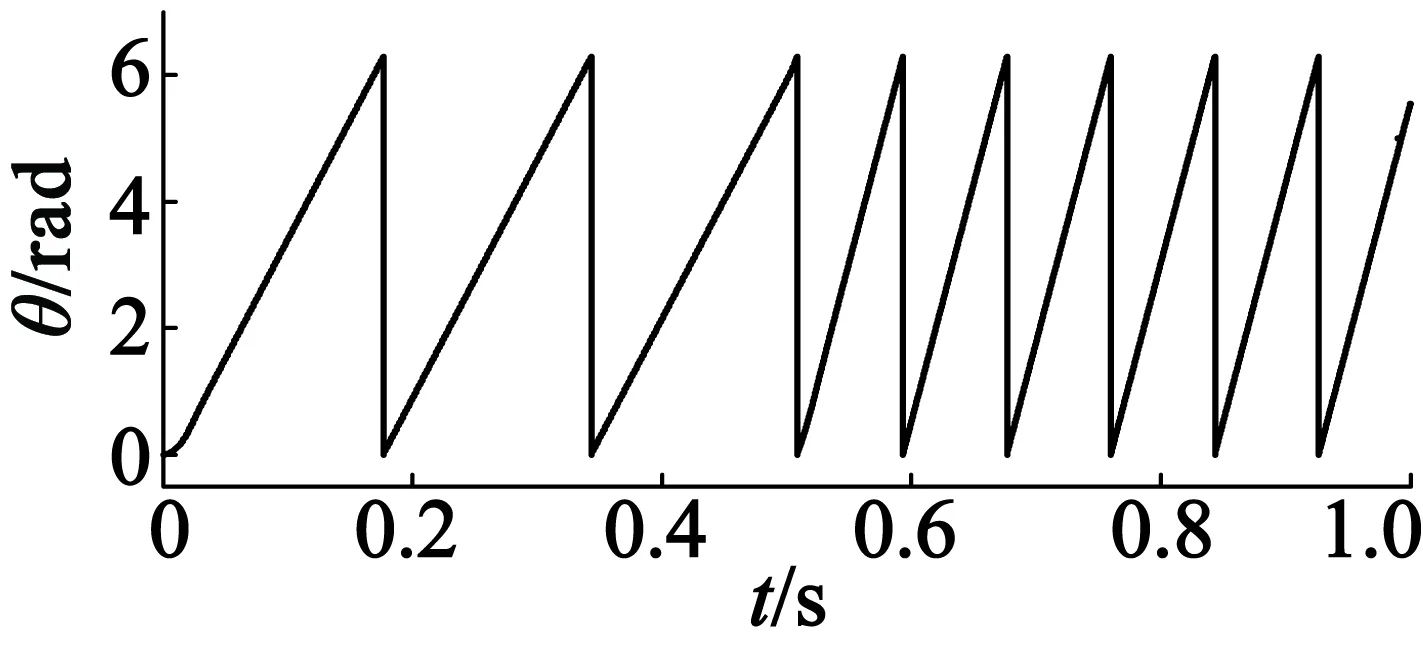
(b) 電機實測位置波形
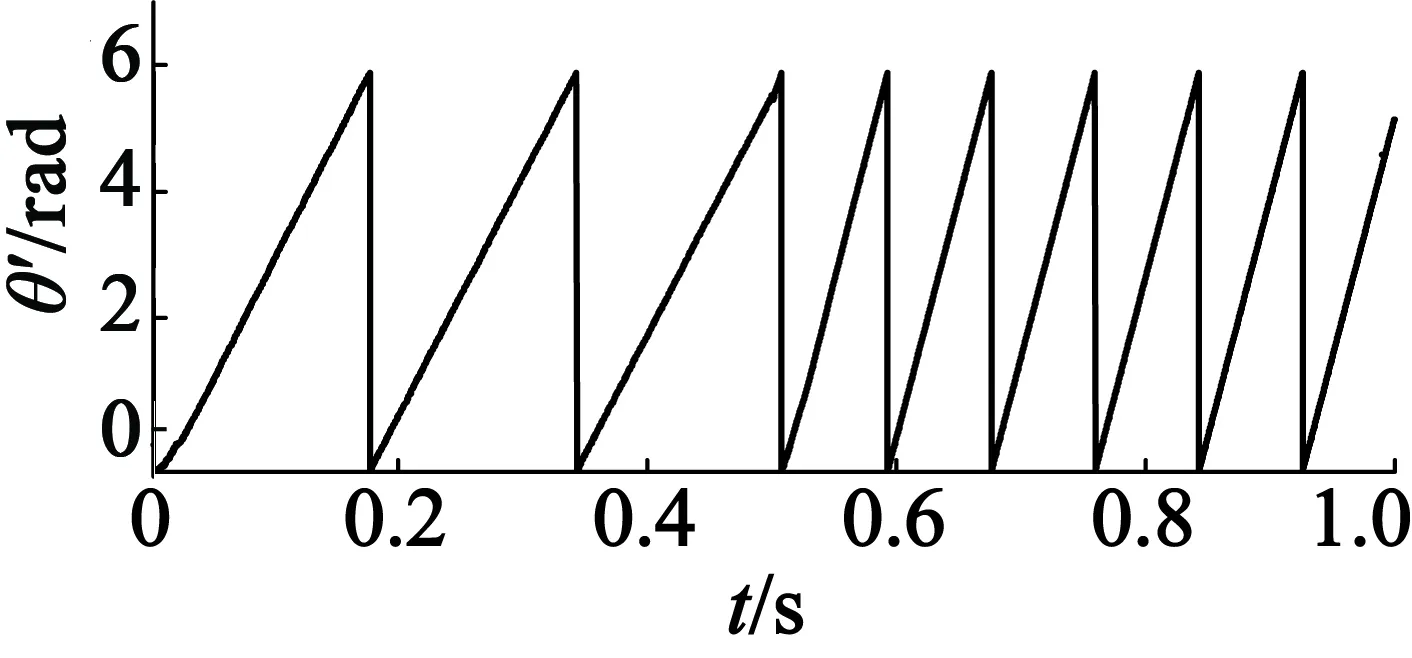
(c) 電機估算位置波形
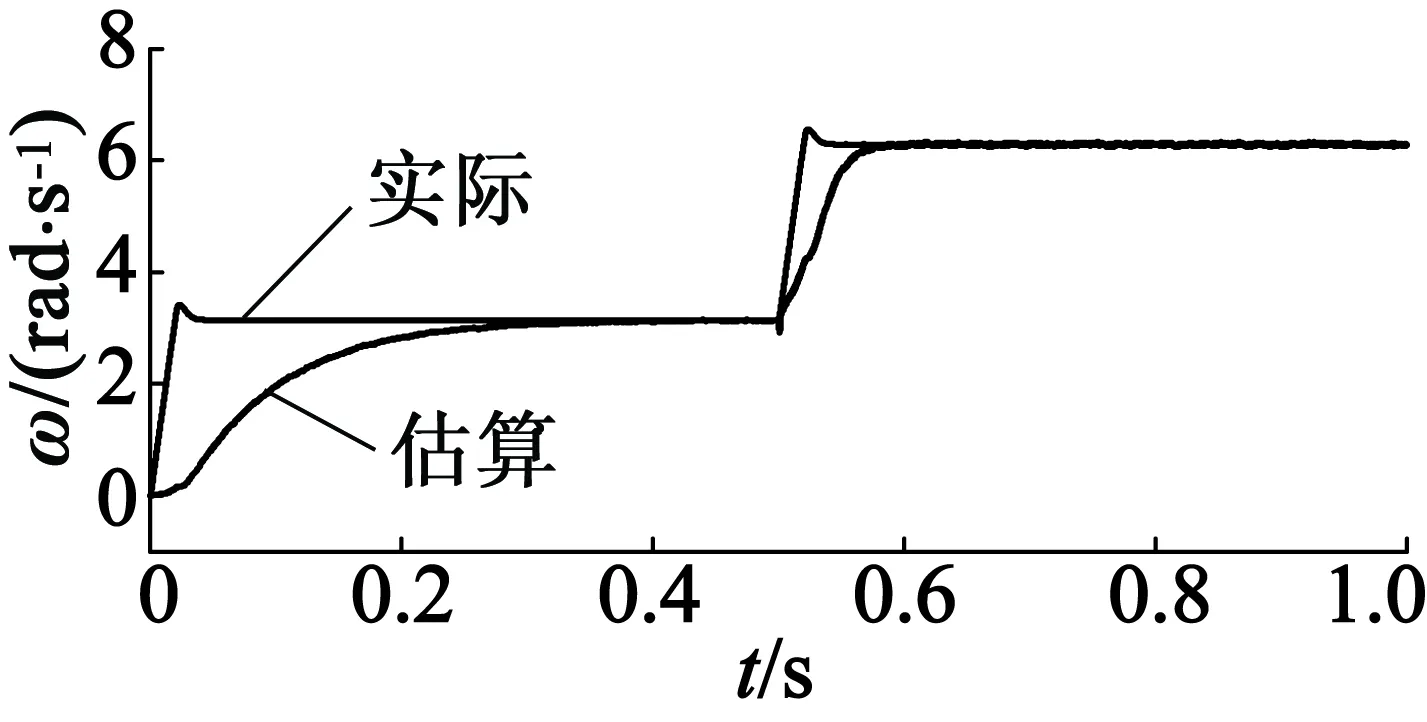
(d) 電機實際轉(zhuǎn)速波形和估算轉(zhuǎn)速波形圖4 轉(zhuǎn)速由30 r/min到60 r/min的突變波形
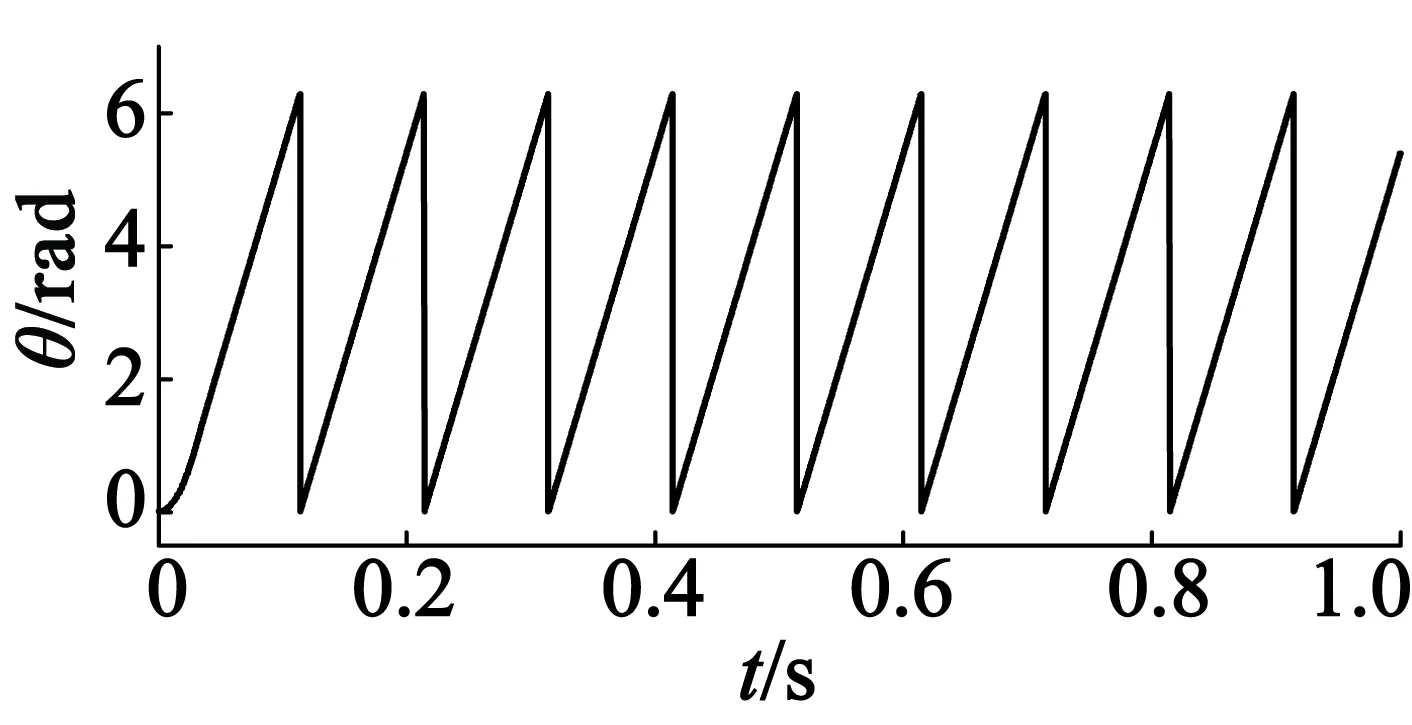
(a) 電機實際位置
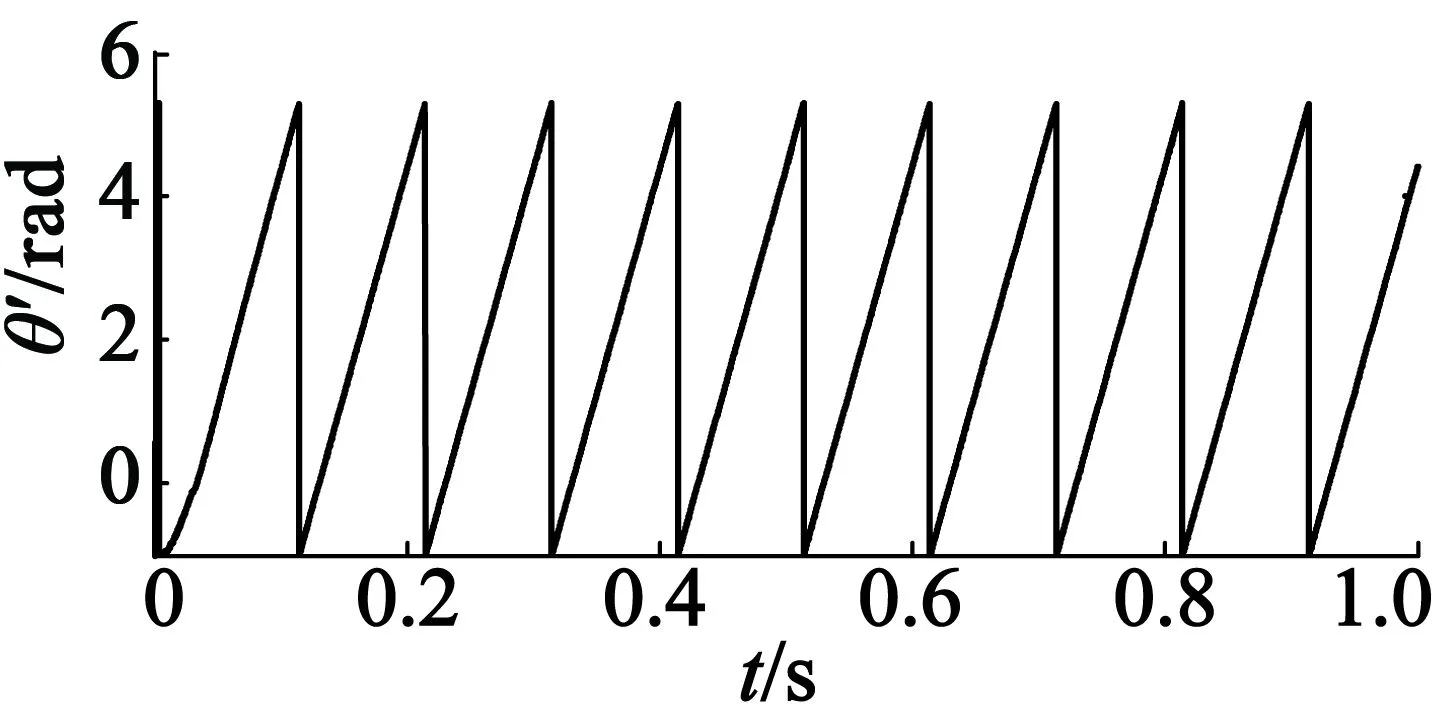
(b) 電機估算位置
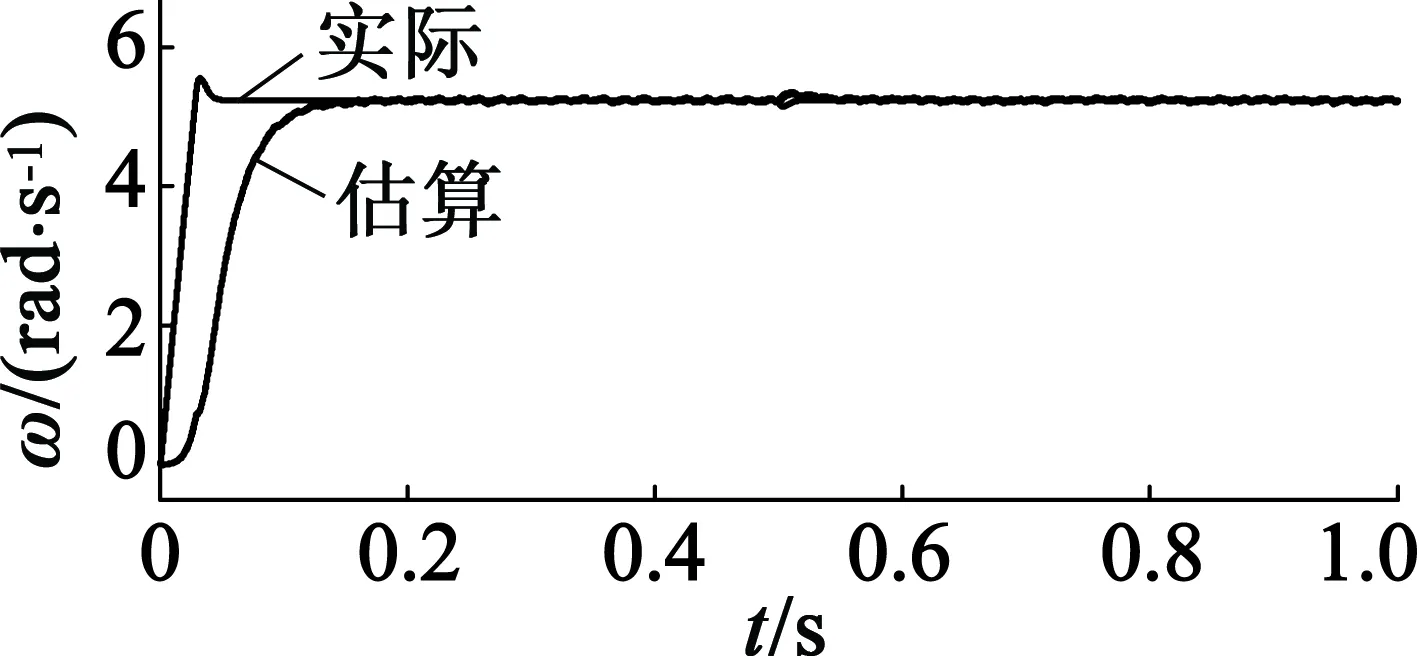
(c) PMSM實際轉(zhuǎn)速和估算轉(zhuǎn)速
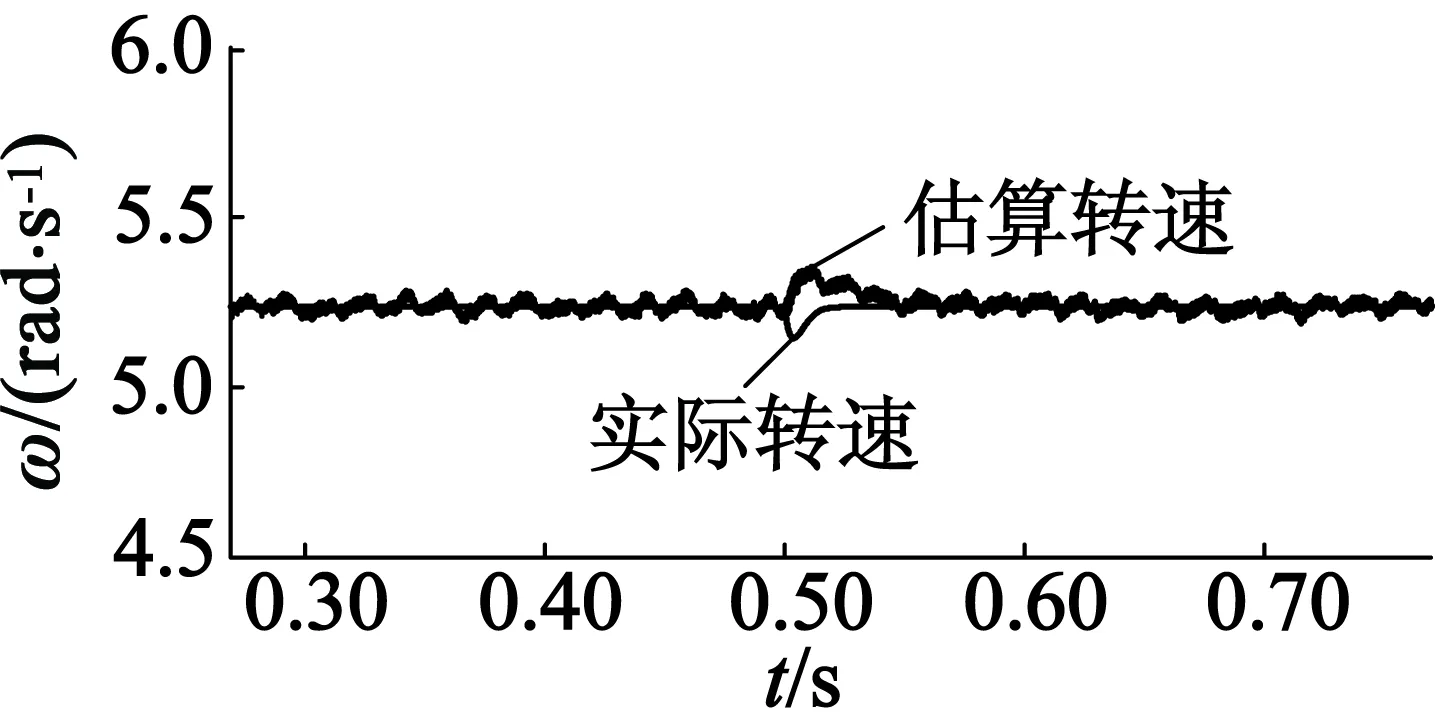
(d) 0.5 s附近負載突變時的轉(zhuǎn)速變化圖5 轉(zhuǎn)速在50 r/min下,0.5 s時負載由 0階躍變化至300 N·m的波形
4 實驗驗證
在上述仿真基礎(chǔ)上,為驗證該位置估算算法的實際效果,搭建基于MRAS無位置傳感器估算的PMSM機矢量控制平臺,驅(qū)動電路使用AD-DC-AC變頻電路,三相逆變電路由智能控制單元IPM構(gòu)成,選用一臺2 kW PMSM作為位置估算對象,電機內(nèi)部參數(shù)與仿真設(shè)置的相同,如表1所示,為驗證算法準(zhǔn)確性,利用增量式編碼器對電機實際位置進行檢測。
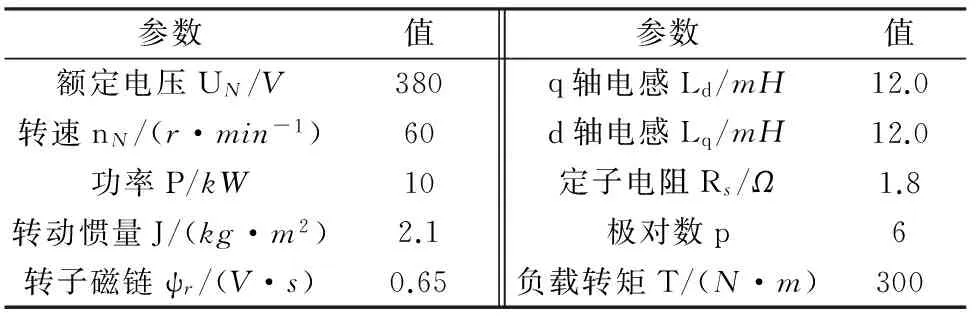
表1 電機內(nèi)部參數(shù)表
由圖6可知,該位置估算算法可以有效跟蹤轉(zhuǎn)子位置,估算位置波形與實測位置波形幾乎重合,但估算位置波形存在一定的波動,這是由實際實驗系統(tǒng)中的一些測量誤差和噪聲造成,同時,由圖6的下半部分可知,估算轉(zhuǎn)速可以有效地跟蹤實際轉(zhuǎn)速,但估算轉(zhuǎn)速落后于實際轉(zhuǎn)速,這是因為MRAS算法實際上是有差拍控制,存在一定的估算延時。

圖6 轉(zhuǎn)速30 r/min,負載轉(zhuǎn)矩300 N·m下的轉(zhuǎn)速 和位置估算波形與位置編碼器實測波形對比
為進一步驗證該位置估算算法的動態(tài)性能,圖7給出了額定負載下,轉(zhuǎn)速給定30r/min階躍至60r/min時的轉(zhuǎn)速和位置估算波形與位置編碼器實測波形對比,由圖7可知,當(dāng)轉(zhuǎn)速發(fā)生突變時,該算法可以有效地跟蹤轉(zhuǎn)速變化,很快地跟蹤上實際的電機轉(zhuǎn)速和位置變化。
5 結(jié) 語
本文將MRAS算法應(yīng)用于PMSM的轉(zhuǎn)子位置與速度估算中,利用Lyapunov穩(wěn)定性理論,基于PMSMα-β坐標(biāo)系下的電流模型,推導(dǎo)出了兩相α-β坐標(biāo)系下的反電勢自適應(yīng)收斂率,從而保證了位置估算系統(tǒng)的穩(wěn)定性。再根據(jù)α-β坐標(biāo)系下的反電勢精確計算出了轉(zhuǎn)子位置與速度,實現(xiàn)了PMSM機位置與轉(zhuǎn)速的估算,并且具有較小的估算誤差和較快的估算速度。仿真和實驗驗證了該算法的有效性和快速性。
[1] 梁艷,李永東.無傳感器永磁同步電機矢量控制系統(tǒng)概述[J].電氣傳動,2003,33(4):4-9.
[2] 李永東,朱昊.永磁同步電機無速度傳感器控制綜述[J].電氣傳動,2009,39(9):3-10.
[3]CONSOLIA,SCARCELLAG,TESTAA.Industryapplicationofzero-speedsensorlesscontroltechniquesforPMsynchronousmotors[J].IEEETransactionsonIndustryApplications,2001,37(2):513-521.
[4]UTKINV,GULDNERJ,SHIJingxin.Slidingmodecontrolinelectromechanicalsystems[M].BocaRaton,US:CRCPress,1999.
[5]UTKINVI.Slidingmodecontroldesignprinciplesandapplicationstoelectricdrives[J].IEEETransactionsonIndustrialElectronics,1993,40(1),23-36.
[6]CHENZ,TOMITAM,DOKIS,etal.Newadaptiveslidingobserversforposition-andvelocity-sensorlesscontrolsofbrushlessDCmotors[J].IEEETransactionsonIndustrialElectronics,2000,47(3):582-591.
[7]JIANGDong,ZHAOZhengming,WANGFei.AslidingmodeobserverforPMSMspeedandrotorpositionconsideringsaliency[C]//ProceedingsofIEEEConferenceonPowerElectronicsSpecialists.IEEE,2008:809-814.
[8]CHUJB,HUYW,HUANGWX.AnimprovedslidingmodeobserverforpositionsensorlessvectorcontroldriveofPMSM[C]//ProceedingsofIEEEConferenceonPowerElectronicsandMotionControl.IEEE,2009:1898-1902.
[9] 蘇健勇,李鐵才,楊貴杰.PMSM無位置傳感器控制中數(shù)字滑模觀測器抖振現(xiàn)象分析與抑制[J].電工技術(shù)學(xué)報,2009,24(8):58-64.
[10]PARASILITIF,PETRELLAR,TURSINIM.SensorlessspeedcontrolofaPMsynchronousmotorbasedonslidingmodeobserverandextendedKalmanfilter[C]//ProceedingsofIEEEConferenceonIndustryApplicationsConference.IEEE,2001:533-540.
[11]SONGC,ZHENGZ,XULY.Sliding-modesensorlesscontrolofdirect-drivePMsynchronousmotorsforwashingmachineapplications[J].IEEETransactionsonIndustryApplications,2009,45(2):582-590.
[12] 齊放,鄧智泉,仇志堅,等.基于MRAS的永磁同步電機無速度傳感器[J].電工技術(shù)學(xué)報,2007,22(4):53-58.
[13] 朱喜華,李穎暉,張敬.基于一種新型滑模觀測器的永磁同步電機無傳感器控制[J].2010,38(13):7-10.
[14] 齊放,鄧智泉,仇志堅,等.一種永磁同步電機無速度傳感器的矢量控制[J].電工技術(shù)學(xué)報,2007,22(10):30-34.
[15] 張承林,張復(fù)琳,王志福,等.無刷直流電動機無位置傳感器控制技術(shù)綜述[J].微特電機,2014,42(2):70-74.
[16] 朱軍,韓利利,汪旭東,等.永磁同步電機無傳感器控制現(xiàn)狀與發(fā)展趨勢.微電機,2013,46(9):11-16.
[17] 魯文其,胡育文,杜栩楊,等.永磁同步電機新型滑模觀測器無傳感器矢量控制調(diào)速系統(tǒng)[J].中國電機工程學(xué)報,2010,30(33):78-83.
[18] 丁文,梁得亮,羅戰(zhàn)強,等.兩級濾波滑模觀測器的永磁同步電機無位置傳感器控制[J].電機與控制學(xué)報,2012,16(11):1-10.
[19] 王寅東.基于新型滑模觀測器的永磁同步電機無位置傳感器控制[D].天津:天津大學(xué),2012.
Position Sensorless Control of Permanent Magnet Synchronous Motor Drive System Based on MRAS
DENGPeng
(Jingchu University of Technology,Jingmen 448000,China)
In order to achieve the position sensorless control of permanent magnet synchronous motor (PMSM), a model reference adaptive system (MRAS) method which was based on the PMSM mathematical model inα-βreference frame was put forward. In this method, the PMSM position estimation model was established according to the Lyapunov stability theory, usingα-axis andβ-axis voltage, current, and their errors inα-βreference frame. The adaptive ratio of the positional parameter was deduced by means of Lyapunov stability theory, ensuring the stability of position estimation system and the convergence of error, and at the same time the position of PMSM rotor can be quickly and efficiently obtained. The simulation results show the reliability and effectiveness of this method.
permanent magnet synchronous motor (PMSM); model reference adaptive system (MRAS); position estimation
2015-11-01
TM341;TM351
A
1004-7018(2016)07-0051-05
鄧鵬(1981-),男,碩士研究生,講師,研究方向為交流電機控制、電動車驅(qū)動控制、計算機控制等。

