太沙基松動土壓力系數的研究

李 君

(鐵道第三勘察設計院集團有限公司,天津 300251)

?

太沙基松動土壓力系數的研究

李 君

(鐵道第三勘察設計院集團有限公司,天津 300251)

從土拱的角度對太沙基松動土壓力公式中的側壓力系數進行了研究，提出了土拱是沿大主應力形成的觀點，并通過Mohr-Coulomb極限平衡應力圓分析，推導了太沙基松動土壓力公式中側壓力系數K的一般表達式,其可用于地基局部沉降、盾構隧道工程的土壓力分析。

松動土壓力，側壓力系數，土拱效應

0 引言

太沙基提出的松動土壓力表達式[1](如式(1)所示)較好地反映了土拱效應的應力轉移現象，被廣泛地應用于計算隧道盾構襯砌豎向土壓力[2]及路堤樁設計[3]中。

(1)

但在式(1)中，側向壓力系數Kh的取值沒有一個確定的計算方法。本文基于前人關于土拱效應理論研究和試驗實測數據的分析，在數值分析的基礎上，提出了土拱是沿大主應力形成的觀點，并通過Mohr-Coulomb極限平衡應力圓分析，推導了太沙基松動土壓力公式中側壓力系數Kh的一般表達式。

1 公式中側向土壓力系數和土拱效應

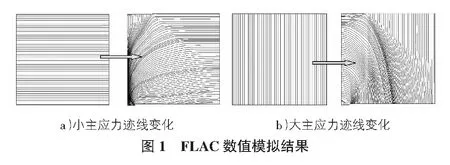
由于隧道開挖等引起的圍巖應力釋放，使得變形土體與周圍穩定土體之間產生一定的相對位移，變形土體通過抗剪能力的發揮，把部分壓力傳遞給了周圍穩定土體，土體內產生了土拱效應。太沙基從土拱應力傳遞的角度出發，提出以松散介質平衡理論為基礎的計算方法，并根據Trapdoor試驗結果建議側向壓力系數為1.0。隨著近些年隧道工程的發展，關于土拱效應的試驗研究也越來越受到重視，國內外有關Trapdoor的砂土模型試驗實測結果發現，Trapdoor達到穩定應力比時，上方土體中心線上的側向壓力系數最大值大于1[4，5]。說明在土拱效應發生前后，Trapdoor上方土體的靜止土壓力應力狀態發生了變化，產生了主應力軸旋轉現象。如圖1所示，數值模擬也得到類似結論[6]。開挖面失穩過程中盾構頂部上方土體出現主應力軸旋轉現象，表明盾構頂部以上土拱區域內最大主應力σ1形成的拱形曲線近似為一條向上拱起的圓弧線。

2 修正的側壓力系數

2.1 計算假定

本文鑒于前人關于土拱效應理論研究和試驗實測數據的分析[4-9]，對太沙基松動土壓力公式中的側向土壓力系數進行修正。取圖2計算模型，假定：

1)假定土體為無粘性土，兩條破壞面豎直貫通。

2)破壞區土體均滿足Mohr-Coulomb極限平衡狀態，整個水平土條單元中主應力恒定。

3)破壞區域內最大主應力σ1軌跡線形成的拱形曲線為一條向上拱起的圓弧線。

2.2 土層單元模型中應力分布

根據以上假定，可以得到土層單元中任意一點的水平應力和垂直應力分別為:

(2)

(3)

式中：σ1，σ3——土層單元大、小主應力；θ——該點大主應力與水平方向的夾角。

該點的側壓力系數為：

(4)

(5)

式中：Ka——主動土壓力系數；φ——土體內摩擦角。

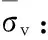
(6)

且注意到破壞面A點θ=θ0,C點θ=-θ0，中心B點θ=0，則有:

(7)

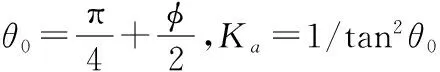
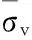
(8)

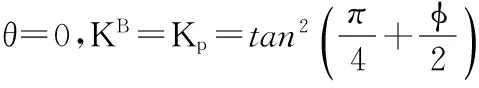
2.3 修正太沙基松動側壓力系數

考慮土拱效應后太沙基松動土壓力分析模型如圖4所示。圖中給出土層單元豎向應力分布，破壞面處豎向土壓力大于土層單元中間豎向土壓力。

土層單元豎向受力平衡方程為:

(9)

式中：B——土條寬度；γ——土的容重；τ——破壞面處的摩擦力。

根據Mohr-Coulomb破壞準則，τ可以表示為:

(10)

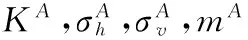
根據式(10)，得到太沙基土拱公式側壓力系數為：

(11)

將式(3)，式(7)代入得:

(12)

其中，θ0=45°+φ/2。

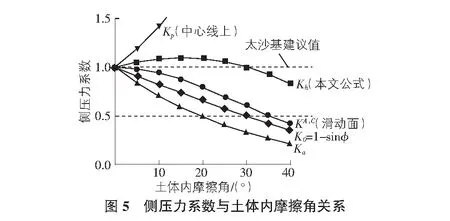
圖5給出等效側壓力系數Kh與內摩擦角的關系。可以看出本文方法計算得到的等效側壓力系數Kh接近1.0，與太沙基建議值和工程經驗取值接近。

3 結語

本文在前人對Trapdoor模型試驗和數值模擬研究的基礎上，提出大主應力拱假設，推導了松散介質考慮土拱效應的側壓力系數，得到以下結論和建議：

1)發生土拱效應的土體，主應力軸旋轉，大主應力軌跡線形成拱型曲線。

2)考慮土拱效應的側壓力系數接近1.0，為工程經驗值提供理論依據。

3)本文公式可用于松散介質中土拱效應的分析和評價，對于粘性土還需開展進一步研究。

[1]TerzaghiK.Theoreticalsoilmechanics.JohnWileyandSons[J].Inc,NewYork,1943(15):37-42.

[2] 孫文昊.土層地層中盾構隧道垂直荷載計算方法探討[J].鐵道工程學報,2009(10):69-73.

[3] 余 闖,劉松玉,杜廣印.樁承式路堤土拱效應的改進Terzaghi方法[J].水文地質與工程地質,2010(4):74-76.

[4] 加 瑞,朱 偉,鐘小春.砂土拱效應的擋板下落試驗及機理研究[J].巖土力學,2006,12(27):687-692.

[5] Adachi T,Kimura M,Kishida K.Experimental study on the distribution of earth pressure and surface settlement through three-dimensional trapdoor tests[J].Tunnelling and Underground Space Technology，2003(18):171-183.

[6] 陳若曦.垃圾填埋場襯墊系統沉陷機理及抗沉陷設計[D].杭州：浙江大學碩士學位論文，2007.

[7] 李永剛,白鴻莉.垂直墻背擋土墻土壓力分布研究[J].水利學報，2003,2(2):102-106.

[8] Handy R L.The arch in soil arching[J].Journal of Geotechnical Engineering,1985,111(3):302-318.

[9] Krynine D P.Discussion of ‘Stability and stiffness of cellular cofferdams’ by Karl Terzaghi[J].Trans.Am.Soc.Civ.Eng.,1945(110):1175-1178.

Study on coefficient of Terzaghi loosening pressure formula

Li Jun

(TheThirdRailwaySurvey&DesignInstituteGroupCorporation,Tianjin300251,China)

From the soil arch, the paper researches the side pressure coefficient in Terzaghi relation soil press formula, soil arch may be depicted as a trajectory of major principal stress that approximates an upward circular arc. Based on the Mohr-Coulomb theory, the modified lateral earth pressure coefficient in Terzaghi loosening pressure formula is presented. It can be used to analyze the earth pressure in the engineering of local subsidence of ground, tunnel and so on.

loosening earth pressure， lateral earth pressure coefficient， soil arching effect

1009-6825(2016)31-0089-03

2016-08-21

李 君(1985- )，男，工程師

TU432

A