基于Simulink的風(fēng)電機(jī)組模糊變槳距控制仿真研究

陳功貴， 黃山外， 劉俊超， 郭 飛

(重慶郵電大學(xué) 自動(dòng)化學(xué)院,復(fù)雜系統(tǒng)分析與控制研究中心，重慶 400065)

?

基于Simulink的風(fēng)電機(jī)組模糊變槳距控制仿真研究

陳功貴， 黃山外， 劉俊超， 郭 飛

(重慶郵電大學(xué) 自動(dòng)化學(xué)院,復(fù)雜系統(tǒng)分析與控制研究中心，重慶 400065)

針對(duì)風(fēng)力發(fā)電系統(tǒng)復(fù)雜非線性的特點(diǎn)，傳統(tǒng)PID控制很難滿足控制系統(tǒng)高精度的要求。在傳統(tǒng)PID控制的基礎(chǔ)上，運(yùn)用模糊理論建立了完整的風(fēng)電機(jī)組變槳距模型，以實(shí)現(xiàn)對(duì)控制系統(tǒng)的實(shí)時(shí)控制。仿真結(jié)果表明,模糊控制能使系統(tǒng)獲得較好的動(dòng)態(tài)特性。利用Simulink進(jìn)行仿真實(shí)驗(yàn)，不僅能使學(xué)生有效理解變槳距控制系統(tǒng)理論知識(shí)，還可以提高學(xué)生的實(shí)驗(yàn)操作能力，從而掌握控制系統(tǒng)的靜態(tài)和動(dòng)態(tài)過(guò)程，這種理論與實(shí)踐相結(jié)合的方法能夠有效地提高教學(xué)質(zhì)量。

風(fēng)力發(fā)電機(jī)； 變槳距控制； 仿真； 模糊控制

0 引 言

風(fēng)能是一種分布廣泛的綠色可再生能源，風(fēng)力發(fā)電機(jī)組能夠?qū)L(fēng)能轉(zhuǎn)換成供人們使用的電能。風(fēng)力發(fā)電系統(tǒng)是一個(gè)多變量、非線性的控制系統(tǒng)，這給風(fēng)電機(jī)組的變槳距控制帶來(lái)了很大的困擾[1]。因此，對(duì)風(fēng)力發(fā)電機(jī)組PID參數(shù)進(jìn)行優(yōu)化來(lái)保證變槳距控制系統(tǒng)的穩(wěn)定性，進(jìn)而得到安全、優(yōu)質(zhì)的電能是是風(fēng)力發(fā)電機(jī)組研究的關(guān)鍵問(wèn)題[2]。而風(fēng)電機(jī)組變槳距控制系統(tǒng)的性能與變槳距控制器的控制規(guī)律及參數(shù)設(shè)置密切相關(guān)，因此，找到合適的控制器參數(shù)成為了變槳距控制的另一個(gè)難題。

維持電力系統(tǒng)安全穩(wěn)定運(yùn)行是非常重要的，對(duì)于這樣一個(gè)復(fù)雜非線性的控制系統(tǒng)，傳統(tǒng)的PID控制[3-4]很難達(dá)到較好的控制效果，而采用模糊PID控制[5-7]，通過(guò)建立模糊規(guī)則對(duì)PID控制參數(shù)進(jìn)行實(shí)時(shí)在線的調(diào)整，這樣能夠使系統(tǒng)獲得良好的動(dòng)態(tài)性能進(jìn)而保證電力系統(tǒng)的穩(wěn)定性[8-10]。本文通過(guò)建立Simulink仿真模快、設(shè)置模塊參數(shù)，在給定風(fēng)速輸入條件下，分別采用PID控制器[11]和模糊PID控制器進(jìn)行仿真實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果表明，模糊控制能使系統(tǒng)獲得更好的動(dòng)態(tài)特性。

將Simulink仿真[12-13]引入到風(fēng)電機(jī)組變槳距控制系統(tǒng)實(shí)驗(yàn)教學(xué)中，學(xué)生可以把所學(xué)的理論知識(shí)運(yùn)用到實(shí)際仿真中，并對(duì)變槳距系統(tǒng)的結(jié)構(gòu)和PID控制原理有深刻的認(rèn)識(shí)，此外，Simulink中直觀詳細(xì)的仿真圖和實(shí)驗(yàn)數(shù)據(jù)，還能培養(yǎng)學(xué)生對(duì)實(shí)驗(yàn)數(shù)據(jù)的處理和分析能力，這種理論與實(shí)踐相結(jié)合的方法能夠有效地提高教學(xué)質(zhì)量[14-15]。

1 風(fēng)電機(jī)組的數(shù)學(xué)模型

風(fēng)力發(fā)電系統(tǒng)是一個(gè)綜合空氣動(dòng)力學(xué)特性，機(jī)械特性及電氣特性為一體的復(fù)雜非線性系統(tǒng)，構(gòu)建風(fēng)電機(jī)組的數(shù)學(xué)模型對(duì)研究系統(tǒng)的動(dòng)態(tài)特性及其控制規(guī)律具有重要意義。在本文中，我們把風(fēng)電機(jī)組模型分為風(fēng)輪模型、傳動(dòng)機(jī)構(gòu)模型和異步發(fā)電機(jī)模型。

1.1 風(fēng)輪模型

風(fēng)輪的作用是將葉片接收到的風(fēng)能轉(zhuǎn)化為機(jī)械能，在輸入風(fēng)速v(m/s)的作用下，風(fēng)輪的吸收功率和氣動(dòng)轉(zhuǎn)矩為：

(1)

式中：P是風(fēng)輪的吸收功率；Tr是風(fēng)輪的氣動(dòng)轉(zhuǎn)矩；Cp是風(fēng)能利用系數(shù)；CT是氣動(dòng)轉(zhuǎn)矩系數(shù)；λ是葉尖速比；β是槳距角；ρ是空氣密度；R是風(fēng)輪半徑。在實(shí)際應(yīng)用中，風(fēng)能利用系數(shù)是由葉尖速比和槳距角共同決定的二元函數(shù)：

(2)

1.2 傳動(dòng)機(jī)構(gòu)模型

本文采用了非直驅(qū)式異步發(fā)電機(jī)組，忽略系統(tǒng)阻力和異步發(fā)電機(jī)的機(jī)械阻力，靠近風(fēng)輪的低速軸和靠近發(fā)電機(jī)的高速軸的動(dòng)態(tài)方程如下：

(3)

式中:Jr為風(fēng)輪轉(zhuǎn)動(dòng)慣量;Jg為發(fā)電機(jī)轉(zhuǎn)動(dòng)慣量；ωr為發(fā)風(fēng)輪轉(zhuǎn)速;n為齒輪箱增速比；Tr為風(fēng)輪輸出轉(zhuǎn)矩;Tm為發(fā)電機(jī)軸機(jī)械轉(zhuǎn)矩;Te為發(fā)電機(jī)電磁轉(zhuǎn)矩。由式(3)可得傳動(dòng)機(jī)構(gòu)方程為：

(4)

1.3 發(fā)電機(jī)模型

本文以異步發(fā)電機(jī)為研究對(duì)象，不考慮導(dǎo)線、鐵芯的集膚效應(yīng)及磁滯、渦流等因素的影響，定子和轉(zhuǎn)子繞組在氣隙中都產(chǎn)生三相對(duì)稱且正弦分布的磁通，異步發(fā)電機(jī)模型可表示為：

(5)

式中:p為發(fā)電機(jī)極對(duì)數(shù);m為相數(shù);U1為發(fā)電機(jī)輸出電壓;C1為修正系數(shù);ω0為電機(jī)同步轉(zhuǎn)速;ωg為發(fā)電機(jī)轉(zhuǎn)子轉(zhuǎn)速;r1、x1分別是定子繞組等效電阻和電抗;r2、x2分別是轉(zhuǎn)子繞組等效電阻和電抗。

2 變槳距PID控制系統(tǒng)仿真模型

在Simulink環(huán)境中建立風(fēng)電機(jī)組變槳距控制系統(tǒng)仿真模型，如圖1所示。變槳距控制系統(tǒng)包含有葉尖速比模塊、PID控制器模塊、風(fēng)能利用系數(shù)模塊、風(fēng)能氣動(dòng)轉(zhuǎn)矩模塊、傳動(dòng)系統(tǒng)模塊、發(fā)電機(jī)模塊。

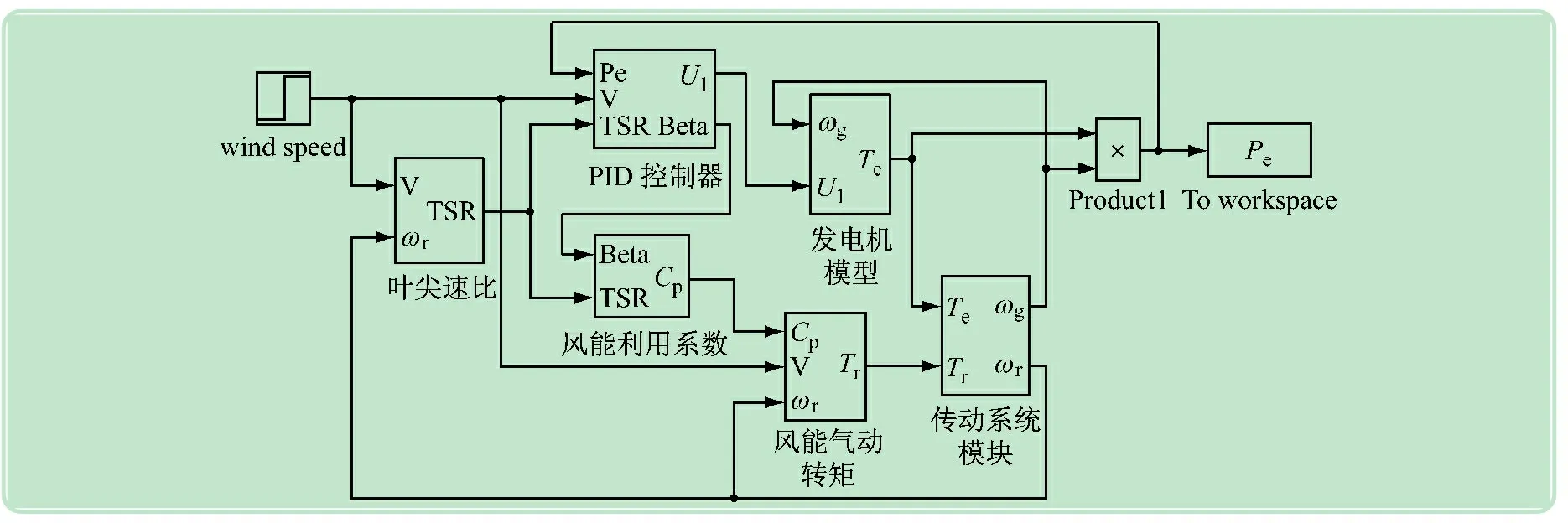
圖1 風(fēng)電機(jī)組變槳距控制系統(tǒng)仿真模型

在給定風(fēng)速下，利用發(fā)電機(jī)額定功率與系統(tǒng)輸出功率的誤差信號(hào)對(duì)槳距角進(jìn)行PID控制。分別改變不同的PID參數(shù)數(shù)值，來(lái)觀察系統(tǒng)輸出隨之而發(fā)生的變化情況。變槳距控制系統(tǒng)PID控制器如圖2所示。

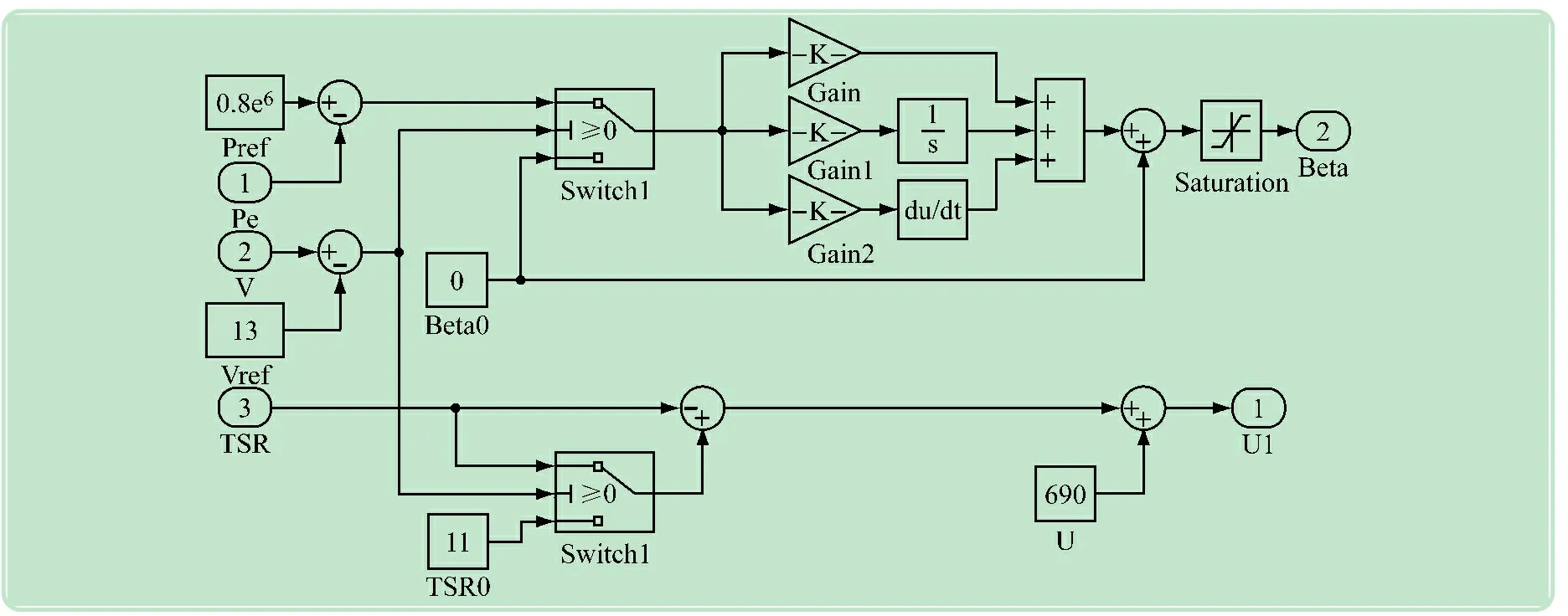
圖2 變槳距控制系統(tǒng)PID控制器

3 模糊PID控制器的設(shè)計(jì)

3.1 模糊PID控制的結(jié)構(gòu)

模糊PID控制器是在傳統(tǒng)PID控制器的基礎(chǔ)上，使用模糊規(guī)則、模糊邏輯推理方法來(lái)調(diào)整PID控制算法中的參數(shù)。其中,由模糊邏輯推理得到的結(jié)果并不直接作為系統(tǒng)的輸出，而是繼續(xù)整定PID參數(shù)，使系統(tǒng)的具有更好的動(dòng)態(tài)性能。其Simulink仿真模塊如圖3所示。

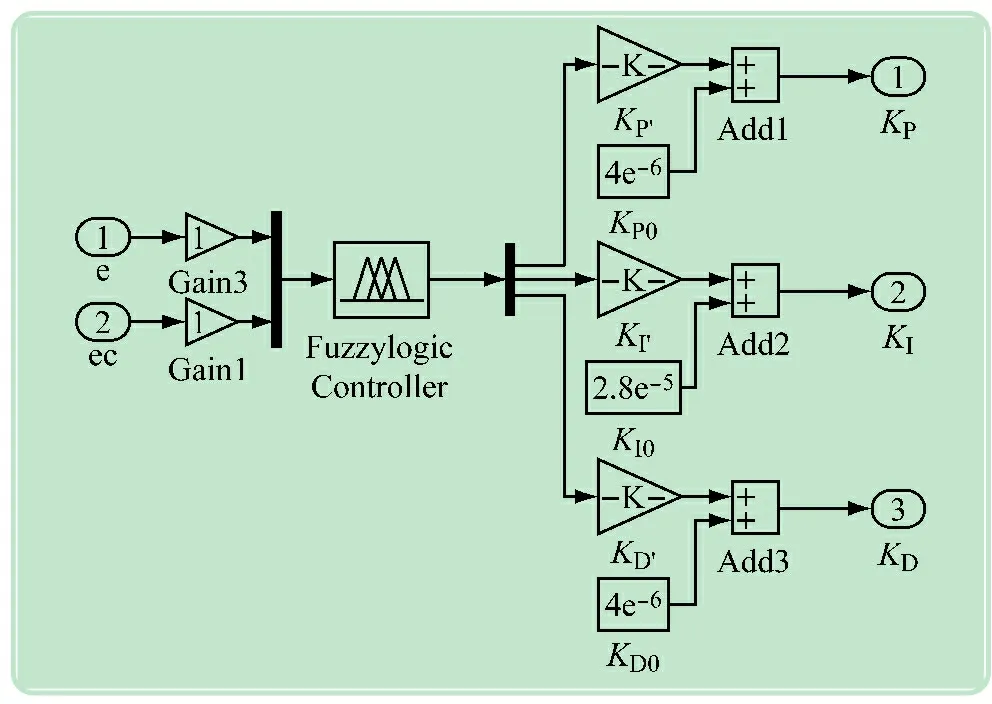
圖3 模糊PID控制器

3.2 模糊控制規(guī)則的設(shè)計(jì)

模糊控制規(guī)則的設(shè)計(jì)步驟如下：

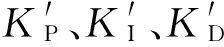
(6)

其中，KP0，KI0，KD0為模糊自適應(yīng)PID控制器的初值，并

設(shè)置為：KP0=4e-6，KI0=2.8e-5，KD0=1e-6。

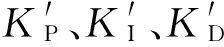
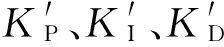
表的模糊控制規(guī)則表

4 仿真實(shí)驗(yàn)及結(jié)果分析

風(fēng)力發(fā)電機(jī)變槳距控制系統(tǒng)動(dòng)態(tài)特性在工程應(yīng)用中是必須進(jìn)行的試驗(yàn)之一，這關(guān)系到風(fēng)電機(jī)組運(yùn)行安全及電能質(zhì)量。仿真實(shí)驗(yàn)所用的風(fēng)力機(jī)組參數(shù)如表4所示，異步發(fā)電機(jī)參數(shù)如表5所示，相關(guān)參數(shù)來(lái)源于德國(guó)Nordex公司S70/1 500 kW風(fēng)力機(jī)組。

表的模糊控制規(guī)則表

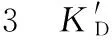
表的模糊控制規(guī)則表

表4 風(fēng)力機(jī)相關(guān)參數(shù)

表5 異步發(fā)電機(jī)相關(guān)參數(shù)

在Matlab/Simulink仿真環(huán)境中，根據(jù)建立的風(fēng)電機(jī)組數(shù)學(xué)模型搭建仿真模塊，在給定風(fēng)速工況下，分別采用PID控制器和模糊PID控制器，并觀察系統(tǒng)動(dòng)態(tài)響應(yīng)過(guò)程，并根據(jù)實(shí)驗(yàn)數(shù)據(jù)及仿真圖對(duì)系統(tǒng)作出具體分析。其中，風(fēng)速初始值設(shè)置為15 m/s，終止值設(shè)置為20 m/s，PID參數(shù)采用傳統(tǒng)PID整定得到的最好結(jié)果，取KP=1.137 5e-5，KI=2.013 3e-5，KD=0.120 9e-5。在Simulink環(huán)境下選擇ode3算法進(jìn)行仿真，分別得到輸出功率、PID參數(shù)、槳距角、葉尖速比、風(fēng)能利用系數(shù)、發(fā)電機(jī)轉(zhuǎn)速的仿真結(jié)果如圖4～9所示。

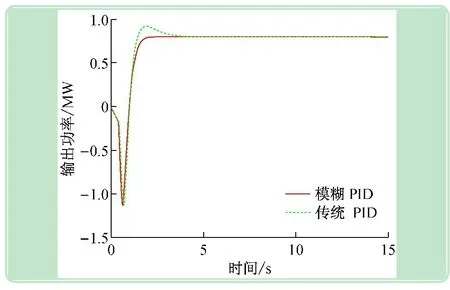
圖4 給定風(fēng)速下的輸出功率

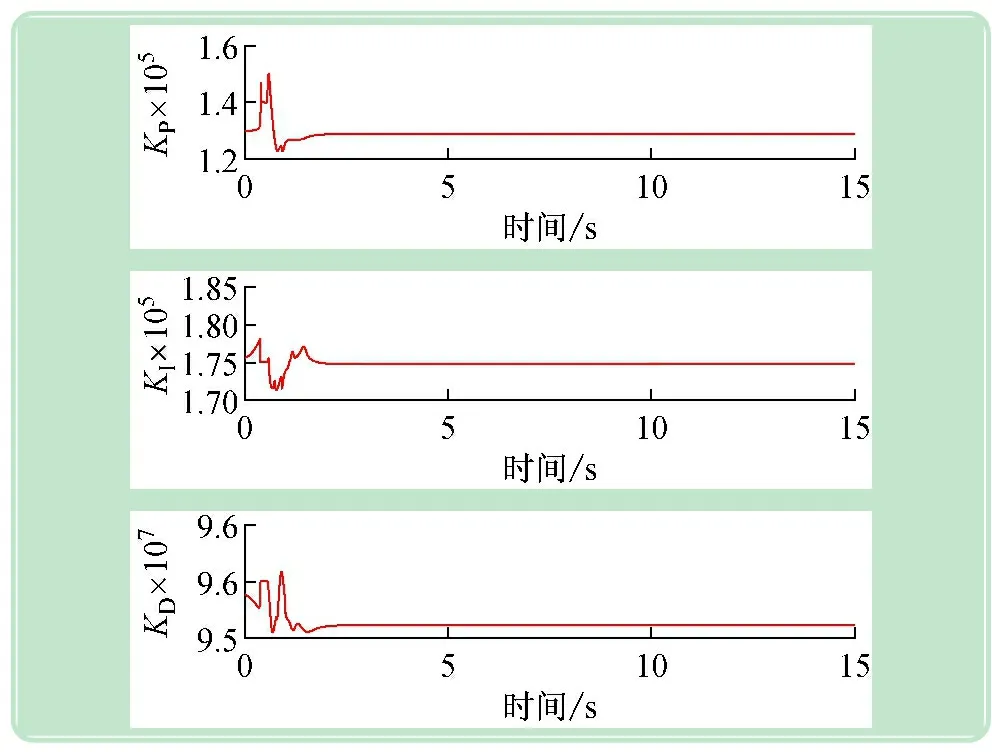
圖5 給定風(fēng)速下PID參數(shù)自適應(yīng)過(guò)程

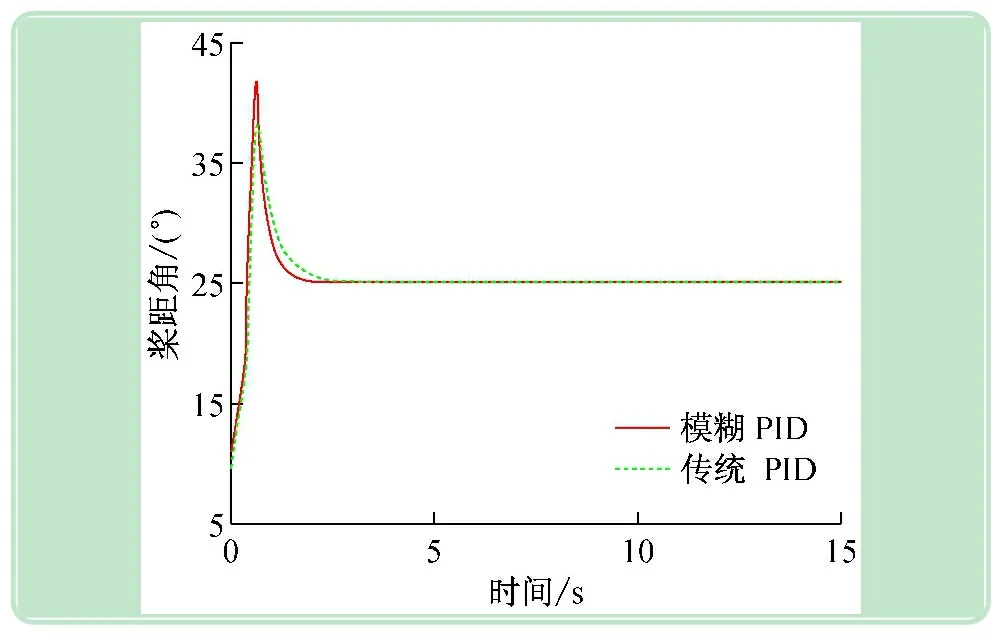
圖6 槳距角

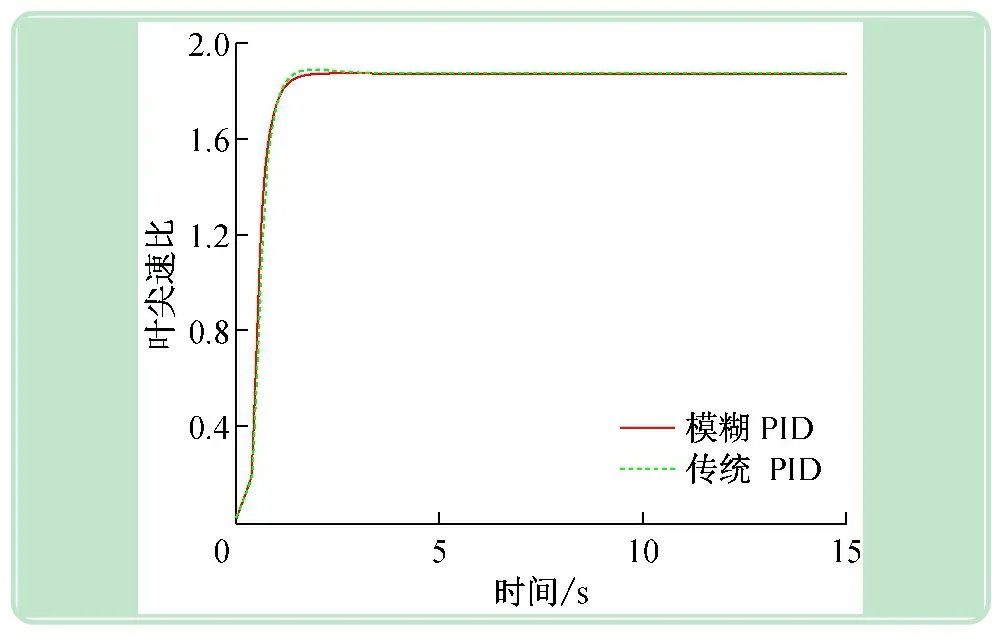
圖7 葉尖速比

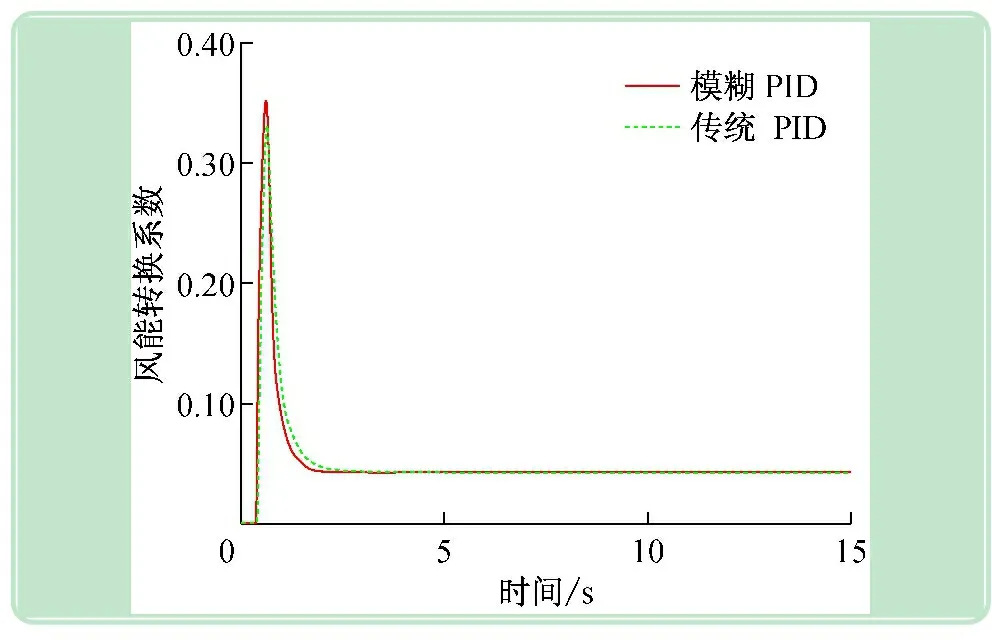
圖8 風(fēng)能轉(zhuǎn)換系數(shù)

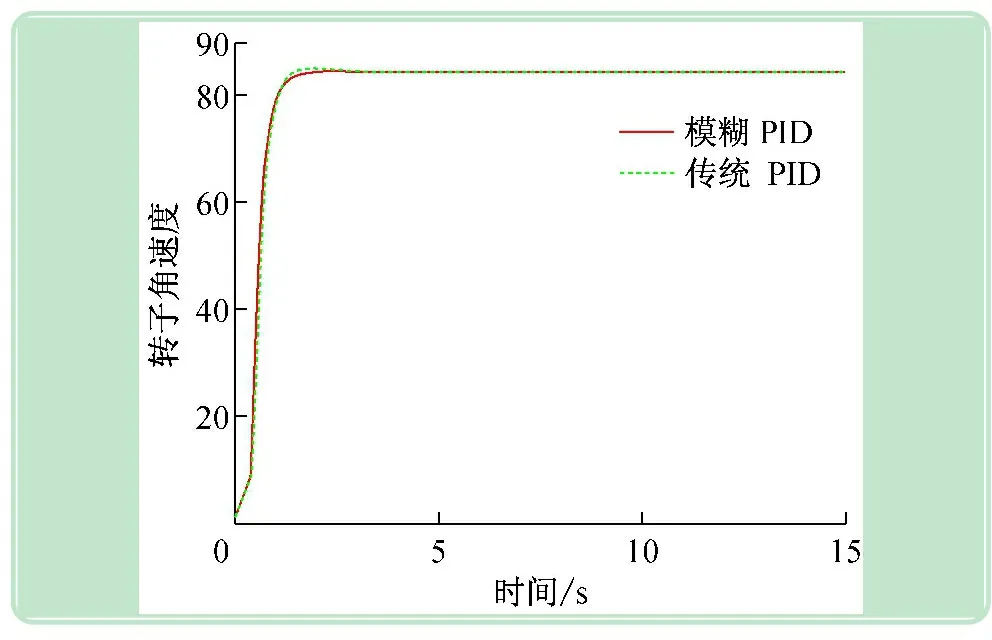
圖9 轉(zhuǎn)子角速度

從圖4中可以看出兩種控制都能使輸出功率穩(wěn)定在額定功率800 kW附近，兩者都有很小的穩(wěn)態(tài)誤差，但傳統(tǒng)PID控制存在較大的超調(diào)量和較長(zhǎng)的調(diào)節(jié)時(shí)間，而模糊PID控制有效地減小了響應(yīng)過(guò)程中的超調(diào)量和調(diào)節(jié)時(shí)間，輸出曲線更為平滑。所以風(fēng)力發(fā)電機(jī)的變槳距控制采用模糊PID控制的動(dòng)態(tài)響應(yīng)性能更好。圖5給出了模糊控制的PID參數(shù)自適應(yīng)過(guò)程，PID參數(shù)的實(shí)時(shí)更新有效的改善了系統(tǒng)的動(dòng)態(tài)性能。圖6～9也顯示模糊PID控制比傳統(tǒng)的PID控制效果更好，更有利于風(fēng)電機(jī)組變槳距控制。

5 結(jié) 語(yǔ)

風(fēng)力發(fā)電系統(tǒng)是一個(gè)綜合了多個(gè)學(xué)科的復(fù)雜系統(tǒng)，本文針對(duì)典型的具有大慣性、大滯后、非線性等特性的風(fēng)力發(fā)電機(jī)變槳距控制系統(tǒng)，建立了相應(yīng)的數(shù)學(xué)模型，并在Matlab/Simulink環(huán)境下搭建了變槳距控制系統(tǒng)仿真模塊。在給定風(fēng)速輸入條件下，運(yùn)用模糊PID控制對(duì)系統(tǒng)進(jìn)行仿真實(shí)驗(yàn)，并將其與傳統(tǒng)PID控制仿真結(jié)果進(jìn)行比較。實(shí)驗(yàn)結(jié)果表明，模糊PID控制是一種更有效的風(fēng)力發(fā)電機(jī)組變槳距控制方法，相比于傳統(tǒng)PID控制，模糊控制的運(yùn)用能使系統(tǒng)擁有更快的響應(yīng)速度，更小的超調(diào)量，更好的穩(wěn)定性。

我們將Simulink仿真引入到實(shí)驗(yàn)研究與教學(xué)中，通過(guò)理論知識(shí)和實(shí)踐仿真相結(jié)合，既能有效地激發(fā)學(xué)生的學(xué)習(xí)興趣，又能培養(yǎng)學(xué)生解決問(wèn)題的能力。Simulink實(shí)驗(yàn)結(jié)果中豐富的實(shí)驗(yàn)數(shù)據(jù)和仿真圖形，使學(xué)生對(duì)理解系統(tǒng)的動(dòng)態(tài)過(guò)程有了更直觀的理解，并對(duì)PID參數(shù)變化引起系統(tǒng)性能的改變有了更深刻的認(rèn)識(shí)。

[1] 宋新甫, 梁 波. 基于模糊自適應(yīng)PID的風(fēng)力發(fā)電系統(tǒng)變槳距控制[J]. 電力系統(tǒng)保護(hù)與控制, 2009,37(16):50-53, 58.

[2] Chen G, Liu L, Song P,etal. Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems[J]. Energy Conversion and Management, 2014(86):548-560.

[3] 白 金, 韓俊偉. 基于MATLAB/Simulink環(huán)境下的PID參數(shù)整定[J]. 哈爾濱商業(yè)大學(xué)學(xué)報(bào), 2007,23(6):673-676.

[4] 王 釗, 陳 真. 基于Simulink的PID控制器設(shè)計(jì)[J]. 實(shí)驗(yàn)技術(shù)與管理, 2007,24(5):70-72.

[5] 陽(yáng) 睿, 李英姿, 張立文, 等. 模糊PID控制的原子力顯微鏡仿真平臺(tái)[J]. 實(shí)驗(yàn)室研究與探索, 2014,33(1):9-12, 153.

[6] 郭 鵬. 模糊前饋與模糊PID結(jié)合的風(fēng)力發(fā)電機(jī)組變槳距控制[J]. 中國(guó)電機(jī)工程學(xué)報(bào), 2010,30(8):123-128.

[7] 孫曉明, 馬 青, 曹 虎, 等. 自適應(yīng)模糊PID控制在PLC變頻調(diào)速同步測(cè)試中的應(yīng)用[J]. 實(shí)驗(yàn)室研究與探索, 2014,33(6):16-18, 64.

[8] 費(fèi)紅姿, 范立云, 費(fèi)景洲, 等. 基于虛擬儀器的直流電機(jī)模糊PID控制實(shí)驗(yàn)研究[J]. 實(shí)驗(yàn)技術(shù)與管理, 2015,32(3):81-84, 96.

[9] 王建偉, 段愛(ài)霞, 侯樹(shù)文. 基于遺傳算法的水輪發(fā)電機(jī)組模糊PID控制研究[J]. 水力發(fā)電, 2007,33(7):60-62.

[10] 俞海珍, 史旭華, 徐建瑜. 模糊自適應(yīng)PID控制在過(guò)程控制實(shí)驗(yàn)系統(tǒng)上的應(yīng)用[J]. 實(shí)驗(yàn)技術(shù)與管理, 2010,27(1):69-72.

[11] 劉金琨. 先進(jìn)PID控制MATLAB仿真[M]. 北京: 電子工業(yè)出版社, 2011.

[12] 尚 麗, 崔 鳴, 杰 陳. Matlab/Simulink仿真技術(shù)在雙閉環(huán)直流調(diào)速實(shí)驗(yàn)教學(xué)中的應(yīng)用[J]. 實(shí)驗(yàn)室研究與探索, 2011,30(1):181-185.

[13] 郭訓(xùn)華, 邵世煌. Simulink建模與仿真系統(tǒng)設(shè)計(jì)方法及應(yīng)用[J]. 計(jì)算機(jī)工程, 2005,31(22):127-129, 145.

[14] 葉杭冶, 潘東浩. 風(fēng)電機(jī)組變速與變槳距控制過(guò)程中的動(dòng)力學(xué)問(wèn)題研究[J]. 太陽(yáng)能學(xué)報(bào), 2007,28(12):1321-1328.

[15] 張 佳. 光電跟蹤系統(tǒng)的模糊自適應(yīng)PID控制實(shí)驗(yàn)[J]. 實(shí)驗(yàn)技術(shù)與管理, 2014,31(8):59-63, 86.

[16] 左 鋒, 石紅瑞, 劉洪瑋. 模糊控制在空氣球?qū)嶒?yàn)系統(tǒng)中的應(yīng)用[J]. 實(shí)驗(yàn)室研究與探索, 2010,29(5):36-38, 42.

·名人名言·

科學(xué)實(shí)驗(yàn)是科學(xué)理論的源泉,是自然科學(xué)的根本,也是工程技術(shù)的基礎(chǔ)。

——張文裕

Research on Fuzzy Variable Pitch Control System for Wind Turbines Based on Simulink

CHENGong-gui,HUANGShan-wai,LIUJun-chao,GUOFei

(Research Center on Complex Power System Analysis and Control, College of Automation,Chongqing University of Posts and Telecommunications, Chongqing 400065, China)

Because of the complexity of nonlinear wind power system, traditional PID control is difficult to meet the requirements of system performance and high accuracy. In order to realize the real-time adjustment of this system, simulation modules are built in Simulink environment, and fuzzy theory is used on the base of traditional PID control. The experimental results manifest that the use of fuzzy control can make the system to achieve better dynamic performance. The simulation experiment with Simulink can not only promote students’ efficient learning and understanding the theoretical knowledge; but also improve their simulation ability so as to grasp the static and dynamic processes of variable pitch control system. This kind of method combines theory and practice, and is effective in improving teaching quality.

wind turbine; variable pitch; simulation; fuzzy PID control

2015-10-22

重慶郵電大學(xué)教育教學(xué)改革項(xiàng)目(XJG1522)；重慶市高等教育教學(xué)改革研究重點(diǎn)項(xiàng)目(132016)

陳功貴(1964-)，男，湖北恩施人，博士，教授，主要從事電氣工程專業(yè)的教學(xué)和科研工作。

Tel.:15310488567;E-mail: chenggpower@126.com

TM 614; G 434

A

1006-7167(2016)04-0090-05