一種在線再入側向制導方法

常江, 馬清華, 王根, 羅建軍

(1.西安現(xiàn)代控制技術研究所 第五技術部, 陜西 西安 710065;2.西北工業(yè)大學 航天學院, 陜西 西安 710072)

?

一種在線再入側向制導方法

常江1, 馬清華1, 王根1, 羅建軍2

(1.西安現(xiàn)代控制技術研究所 第五技術部, 陜西 西安 710065;2.西北工業(yè)大學 航天學院, 陜西 西安 710072)

側向制導是飛行器再入制導的重要組成部分,由于傳統(tǒng)側向制導方法不能對傾側角反轉次數(shù)進行在線優(yōu)化,往往會給再入飛行器姿態(tài)控制系統(tǒng)的設計帶來沉重負擔。為此,利用偽譜法可在線快速求解優(yōu)化問題的特點,提出了一種基于偽譜法的在線再入側向制導方法,并結合縱向預測校正制導法進行再入制導解算以縮減優(yōu)化規(guī)模。仿真結果表明,在保證制導精度的前提下,所提方法有效地減少了傾側角反轉次數(shù)。

再入飛行器; 側向制導; 預測校正; 偽譜法

0 引言

再入飛行器的側向運動一般通過傾側角符號變化來實現(xiàn)。由于傾側角大范圍反轉通常會引發(fā)惡劣的氣動特性并使姿態(tài)控制系統(tǒng)面臨巨大挑戰(zhàn)[1],故側向制導時,在滿足精確性要求的前提下希望傾側角反轉次數(shù)最少。

通常,側向制導方法分為參考軌跡跟蹤和傾側角反轉邏輯兩大類:文獻[2-3]基于非線性幾何法或最優(yōu)控制實現(xiàn)了對縱、側向參考軌跡的同時跟蹤;文獻[4-5]把橫程或橫程變化率作為控制傾側角反轉的變量,當變量超出預先設計的走廊時傾側角發(fā)生反轉。然而,上述側向制導方法不能兼顧嚴格限制傾側角反轉次數(shù)和高精度再入對在線制導的需求,故本文提出利用偽譜法的高精度和快速收斂性,在線對傾側角符號變化規(guī)律進行優(yōu)化設計,從而實現(xiàn)傾側角反轉次數(shù)較少的側向制導。不同于文獻[6-7]中對包含縱向、側向的再入運動方程進行帶過程約束和終端約束的優(yōu)化求解,本文利用預測校正法進行滿足再入過程約束和縱向終端約束的縱向制導解算,只對側向運動方程進行僅滿足側向終端約束的優(yōu)化求解,減小了優(yōu)化規(guī)模和時間,有利于在線實施。

1 縱向預測校正制導方法

不考慮地球旋轉,假設側滑角為零,半速度坐標系下的再入飛行器縱向運動方程[8]如下:

(1)

式中:V為速度;m為質量;r為地心距;γ為航跡角;L為升力;D為阻力;常數(shù)μ=gr2。控制變量為傾側角σ和氣動力解算中的迎角α。迎角通常采用預設方案,縱向再入制導只對傾側角大小變化規(guī)律進行設計。

飛行器安全再入所必須滿足的熱流率、過載、動壓和準平衡滑翔等過程約束的交集稱為再入走廊[9],如下式所示:

(2)

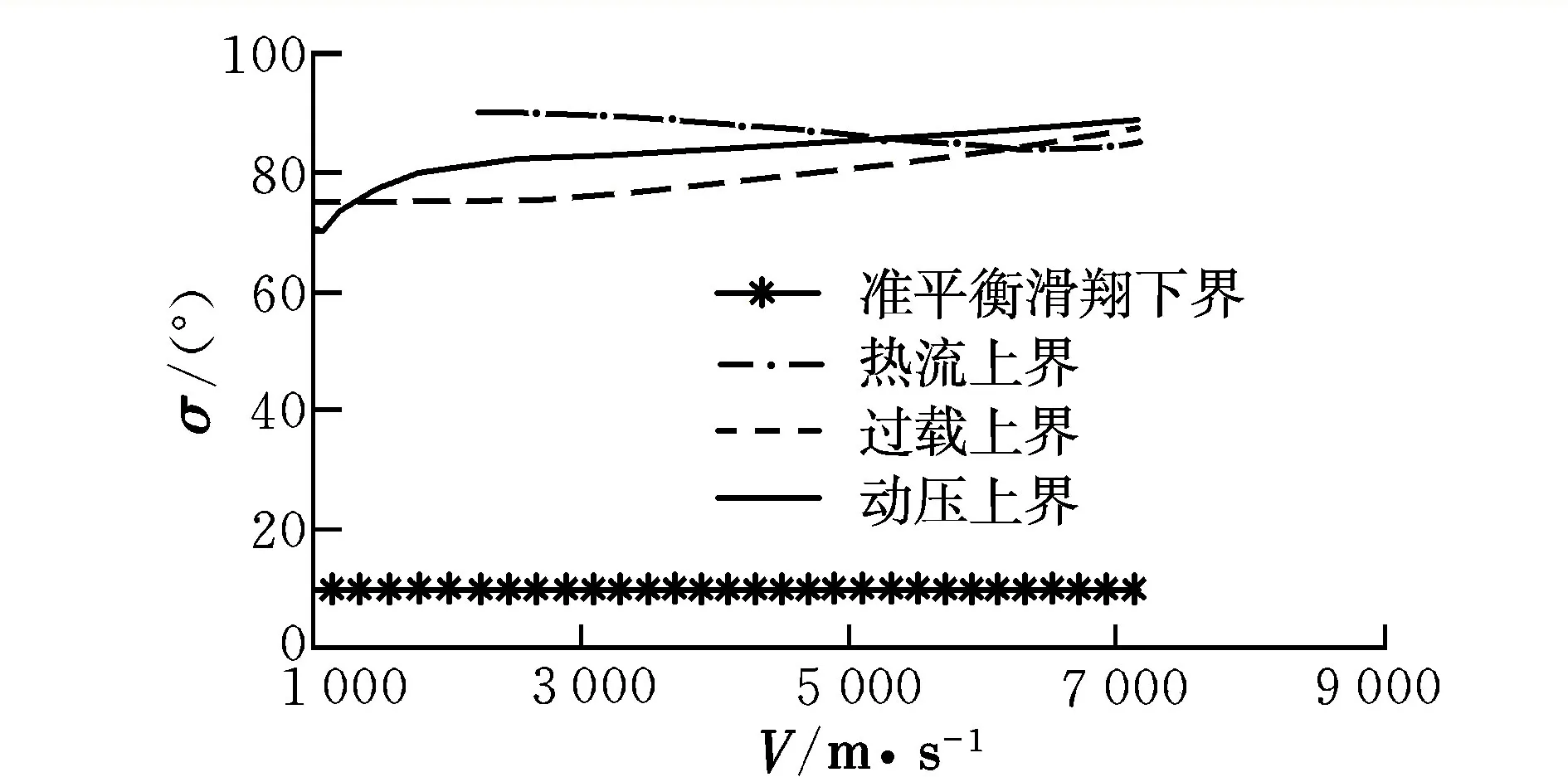
圖1 傾側角邊界Fig.1 Boundary of bank angle

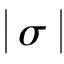
(3)

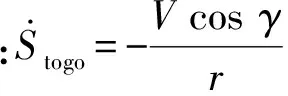
(4)

2 在線再入側向制導方法

2.1 側向運動模型

再入飛行器側向運動方程[8]如下:

(5)

式中:θ為經度;ξ為緯度;φ為航向角。

2.2 約束條件

由于熱流率、動壓、過載和準平衡滑翔約束等過程約束在縱向預測校正方法中被轉化為傾側角絕對值的約束,而終端高度和速度約束只與傾側角絕對值有關,故側向制導優(yōu)化中只需引入如下終端約束:

(6)

式中:Δφ=φ-Φ,Φ的計算公式如下:

(7)

式中:(θT,ξT)為目標點的經緯度。

2.3 優(yōu)化性能指標

傾側角的絕對值由縱向預測校正制導決定,故半速度坐標系中總升力L的側向分量Lsinσ的絕對值也隨之確定,唯一的可變量是Lsinσ的符號,即傾側角的符號。為了有效減少傾側角反轉次數(shù),本文在側向制導設計中引入了優(yōu)化的思想,令

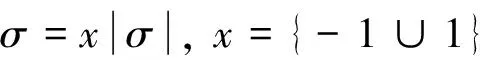
(8)

即側向制導優(yōu)化中控制變量為式(8)中的x,其值取1或-1。

設再入初始時刻變量n為0,其值隨式(8)中控制變量x取值的每次改變而加1,直至再入段結束為止。取優(yōu)化目標函數(shù)為:

J=n

(9)

即Bolza型性能指標函數(shù)中僅有終端性能指標項(傾側角反轉次數(shù)之和),而無狀態(tài)變量和控制量的積分性能指標項。

2.4 高斯偽譜優(yōu)化

根據(jù)上述約束及目標函數(shù),利用高斯偽譜法進行優(yōu)化計算。基于數(shù)值近似方法,高斯偽譜法可對連續(xù)最優(yōu)控制問題在一系列高斯點上進行離散,并轉換為非線性規(guī)劃問題(NLP)[12-13]。其描述如下:

求離散控制變量Uk和狀態(tài)變量Xk、終端時刻tf和初始時刻t0,使得如下性能指標最小:

(10)

并在配點處滿足狀態(tài)約束

(11)

其終端狀態(tài)約束為:

(12)

邊界條件為:

ψ(X0,t0,Xf,tf)=0

(13)

過程約束為:

C(Xk,Uk,τk;t0,tf)≤0

(14)

上述非線性規(guī)劃問題中設計變量包括最優(yōu)控制問題的控制變量(U1,…,Uk)、狀態(tài)變量(X0,X1,…,Xk)以及終端時刻tf和初始時刻t0,并滿足由動力學微分方程約束轉換而來的相應代數(shù)約束、邊界條件ψ=0以及過程約束(C1,…,Ck)。

本文選取魯棒性強、收斂性好的SNOPT算法[14]對上述轉化后的非線性規(guī)劃問題進行求解,從而得到優(yōu)化后的傾側角符號變化規(guī)律。本文再入制導邏輯如圖2所示。

3 仿真算例與分析

以RLV 驗證樣機X-33為對象,給定再入段初始點各運動參數(shù),設置仿真條件與指標如下:

(1)積分采用四階龍格-庫塔方法,步長為1 s;

(2)每20 s進行一次縱向、側向再入制導解算;

(3)取中末制導交接允許誤差范圍為終端約束:高度偏差不大于1 km,經緯度偏差不大于0.05°,終端速度在800～1 100 m/s范圍內。

保證縱向統(tǒng)一采用預測校正方法解算,而側向分別采用本文提出的在線再入側向制導方法和經典的橫程邊界法[1]分別進行解算,為權衡優(yōu)化時間和精度,在線再入側向制導方法優(yōu)化中選取配點數(shù)為30。兩種方法的仿真結果如圖3～圖8所示。

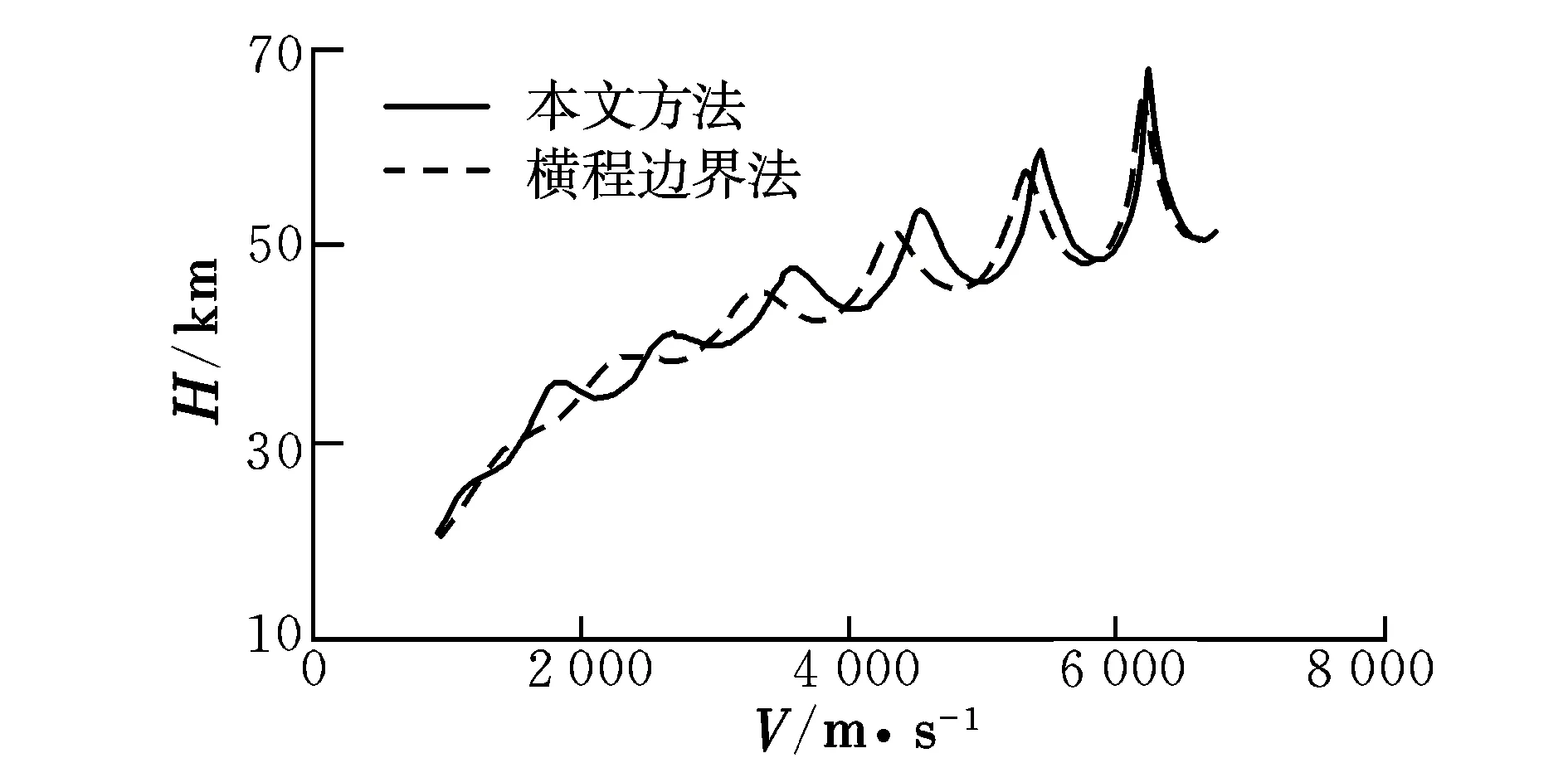
圖3 高度-速度曲線Fig.3 Curves of altitude-velocity

圖4 三維軌跡曲線Fig.4 Curves of 3-D trajectory

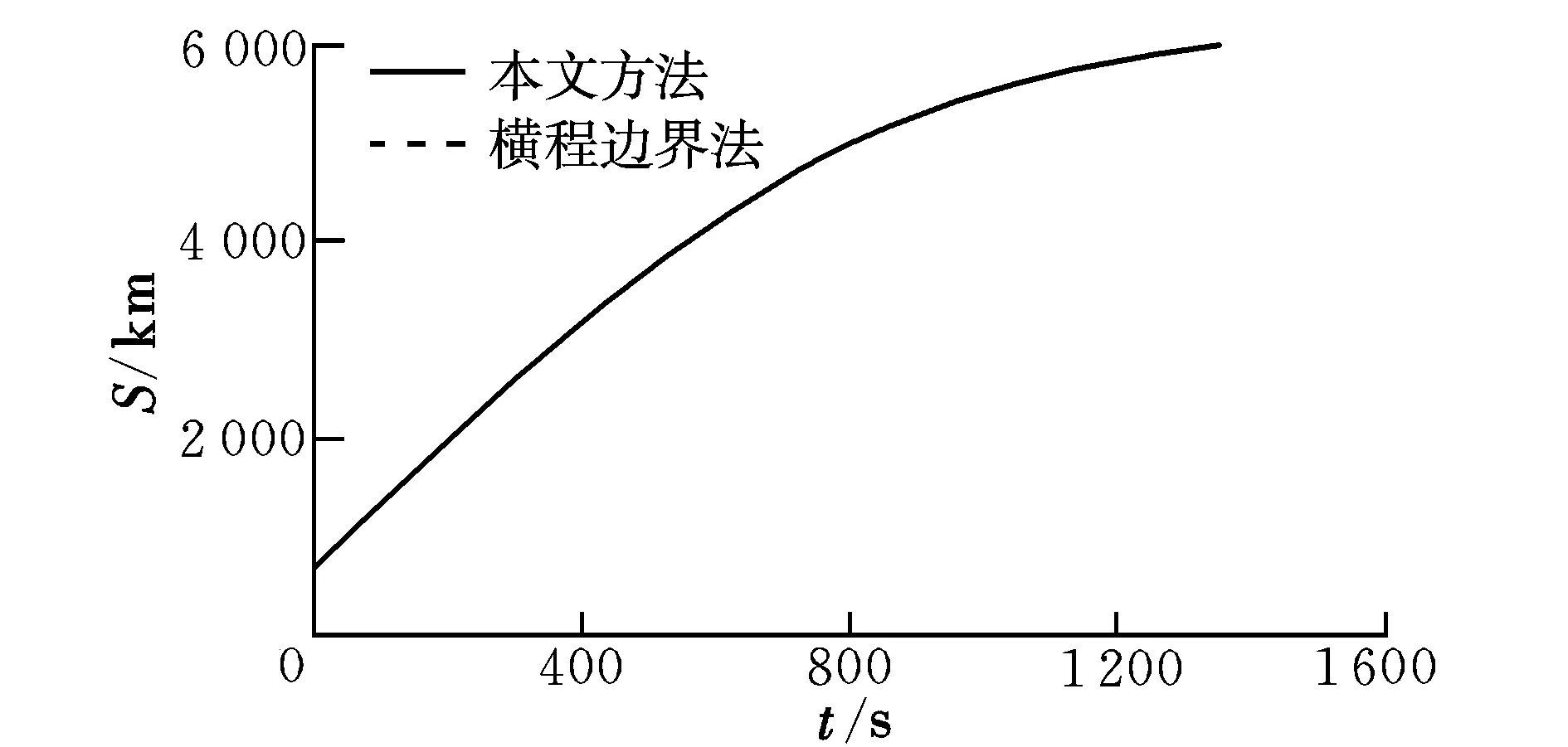
圖5 射程曲線Fig.5 Curves of range

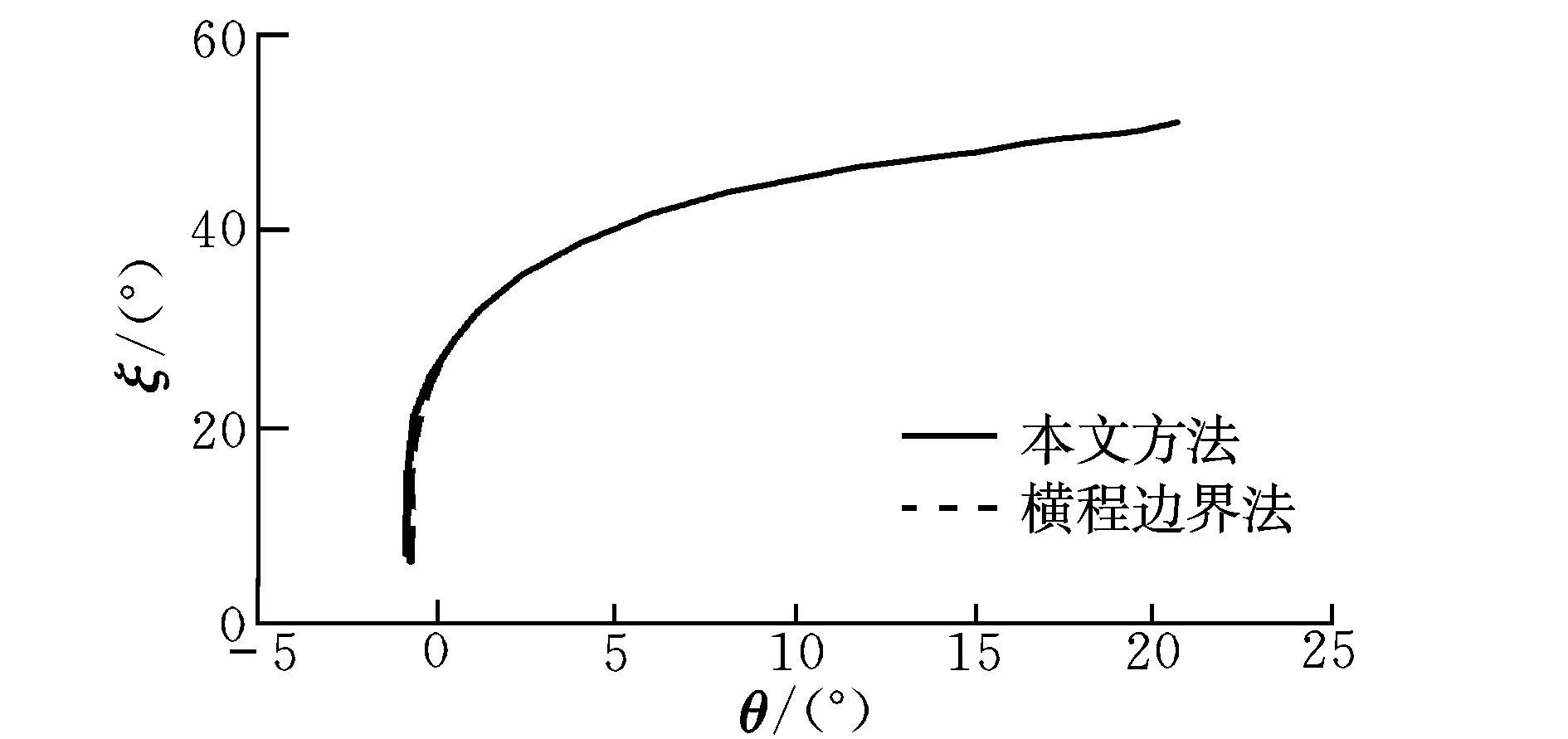
圖6 經緯度曲線Fig.6 Curves of longitude-latitude

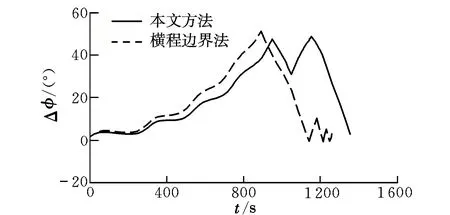
圖7 航向角誤差曲線Fig.7 Curves of heading angle error

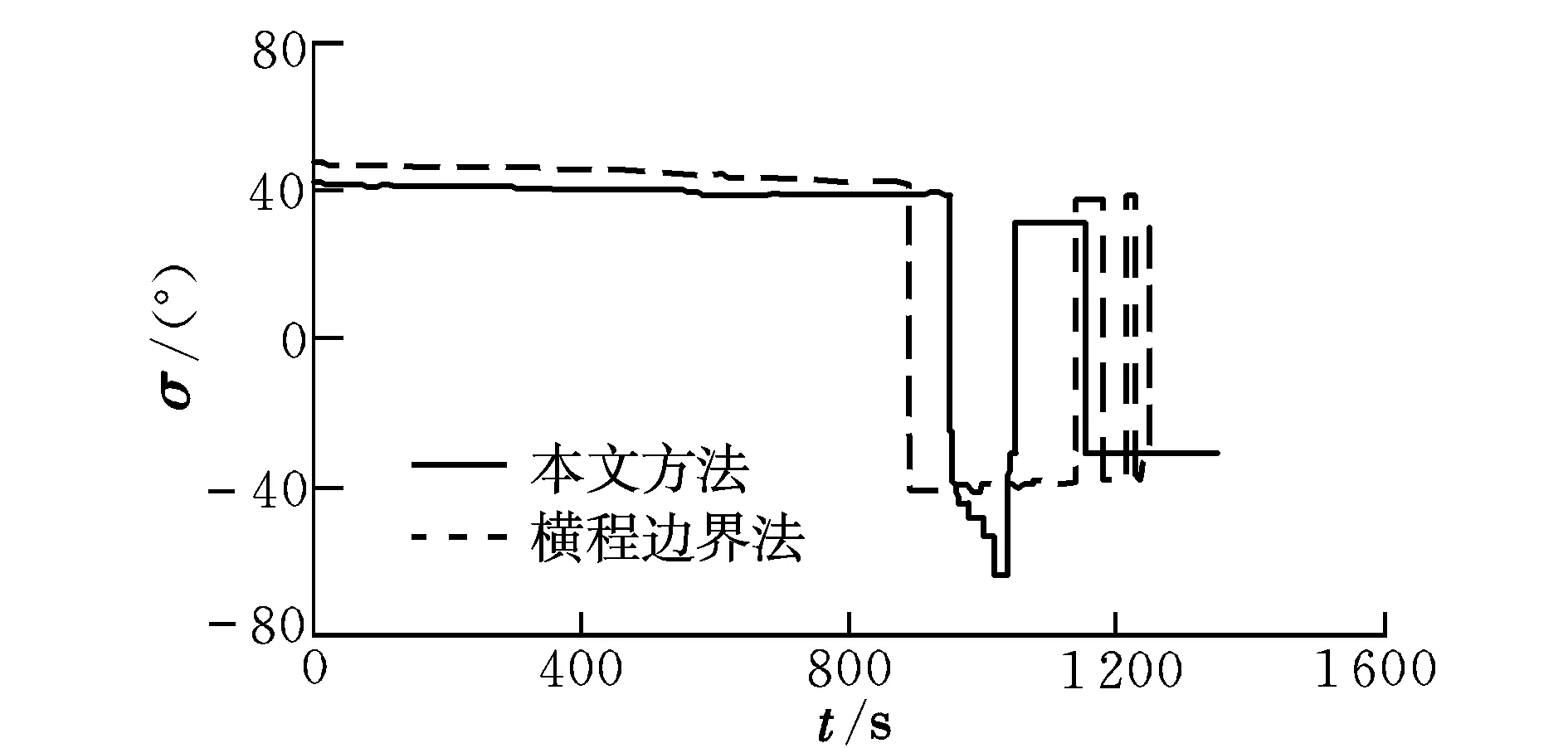
圖8 傾側角曲線Fig.8 Curves of bank angle

仿真計算在CPU為Intel Pentium Dual E2180@ 2.00 GHz,內存為 1 GB,操作系統(tǒng)為Windows XP 的微機上實現(xiàn),在Matlab環(huán)境下編程,每周期制導解算平均用時10.5 s,滿足在線制導要求。采用在線再入側向制導方法的仿真終端參數(shù)與目標值對比結果如表1所示。

表1 終端軌跡參數(shù)對比

Table 1 Comparison of terminal trajectory parameters

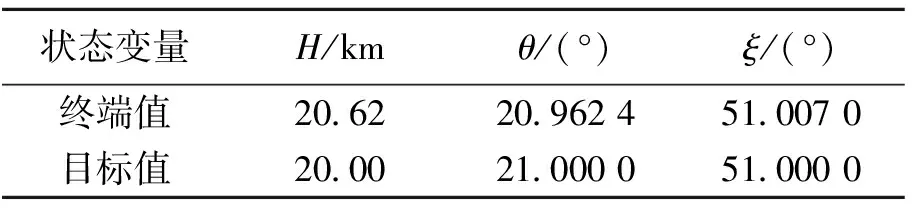
狀態(tài)變量H/kmθ/(°)ξ/(°)終端值2062209624510070目標值2000210000510000

由仿真結果可知,終端經度誤差、緯度誤差、高度誤差、航向角誤差均滿足指標要求,傾側角在再入走廊邊界允許的范圍內變化。結合圖8可知，在線再入側向制導方法的3次傾側角反轉與橫程邊界法的6次傾側角反轉相比,在保證制導精度的同時有效減少了傾側角反轉次數(shù),說明了本文提出方法的有效性。

4 結束語

本文提出了一種在線再入側向制導方法,在縱向采用預測校正方法確定傾側角絕對值的前提下,利用高斯偽譜法在線優(yōu)化解算傾側角符號變化規(guī)律,最終將傾側角作為控制變量帶入到再入運動方程中。與經典的橫程邊界法相比,本文提出的在線再入側向制導方法在保證制導精度的同時有效減少了傾側角反轉次數(shù),可減輕飛行器再入過程中由傾側角大范圍反轉給控制系統(tǒng)帶來的沉重負擔。

[1] Hanson J M,Jones R E.Test results for entry guidance methods for space vehicles [J].Journal of Guidance,Control,and Dynamics,2004,27(6):960-966.

[2] Eduardo G L.Analytic development of a reference trajectory for skip entry[J].Journal of Guidance,Control,and Dynamics,2011,34(1):311-317.

[3] 王麗英,張友安.基于偽譜法的固定采樣實時最優(yōu)制導方法研究[J].宇航學報,2012,33(11):1586-1592.

[4] Shen Zuojun,Lu Ping.Dynamic lateral entry guidance logic [J].Journal of Guidance,Control,and Dynamics,2004,27(6):949-959.

[5] Luo Zongfu,Zhang Hongbo.Patched corridor:a novel lateral logic for skip entry guidance [J].Journal of Guidance,Control,and Dynamics,2014,37(5):1651-1657.

[6] 水尊師,周軍,葛致磊.基于高斯偽譜方法的再入飛行器預測校正制導方法研究[J].宇航學報,2011,32(6):1249-1255.

[7] 楊良,鄭宗貴,徐衡,等.多約束在線高斯偽譜末制導方法[J].彈道學報,2014,26(3):98-103.

[8] Lu Ping.Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1067-1075.

[9] Shen Zuojun,Lu Ping.Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):111-121.

[10] Lu Ping.Asymptotic analysis of quasi-equilibrium glide in lifting entry flight[J].Journal of Guidance,Control,and Dynamics,2006,29(3):662-670.

[11] Joshi Ashok,Sivan K,Savithri A S.Predictor-corrector entry guidance algorithm with path constraints for atmospheric entry vehicles[J].Journal of Guidance,Control,and Dynamics,2007,30(5):1307-1318.

[12] Bollino K,Ross I M,Doman D.Optimal nonlinear feedback guidance for reentry vehicles[R].AIAA-2006-6074,2006.

[13] Ross I M,Sekhavat P,Fleming A,et al.Pseudo-spectral feedback control:foundations,examples and experimental results[R].AIAA-2006-6345,2006.

[14] Gill P E,Walter M,Saunders M A.SNOPT:an SQP algorithm for large-scale constrained optimization [J].SIAM Review,2005,47(1):99-131.

(編輯：崔立峰)

An on-line method of lateral reentry guidance

CHANG Jiang1, MA Qing-hua1, WANG Gen1, LUO Jian-jun2

(1.The fifth department, Xi’an Modern Control Technology Research Institute, Xi’an 710065, China; 2.School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Lateral guidance is an important part of reentry guidance of flight vehicles. However, the traditional lateral guidance method lacks the ability of on-line optimization, which leave attitude control system the burden of a great deal of bank angle-reversals. So in this paper, an optimized designing method working in real-time was proposed based on the high precision and convergence speed of pseudo-spectral method, and combined the longitudinal predictor-corrector method to reduce the size of optimal design. Simulation results show the effectiveness of the proposed method in reducing the number of bank-angle reversals.

reentry vehicle; lateral guidance; predictor-corrector; pseudo-spectral method

2015-12-07;

2016-02-05;

時間:2016-02-26 13:51

常江(1990-)，男，陜西榆林人，工程師，碩士，主要從事飛行器制導與控制研究。

V448.2

A

1002-0853(2016)06-0063-04