基于“底線思維”的應急物資分配-運輸兩層魯棒規劃模型

于 輝，曲亞萍

(重慶大學 經濟與工商管理學院，重慶 400044)

?

基于“底線思維”的應急物資分配-運輸兩層魯棒規劃模型

于 輝，曲亞萍

(重慶大學 經濟與工商管理學院，重慶 400044)

非常規突發事件的應對需要“底線思維”，從“最壞、最困難”的角度展開研究. 為此，針對應急物資的分配與運輸的應急規劃問題提出基于“底線思維”的兩層魯棒模型. 頂層模型從成本最小化的角度確定應急資源的最優配置量，而底層模型從節約時間的角度對頂層的分配方案實施運輸配送，及時、有效地實現應急資源分配的協同優化，最大程度地減少災難帶來的損失. 該模型刻畫了災區物資需求的極度缺失性，在“最壞”情景下利用分解技術研究應急分配與運輸的協同過程，不僅揭示了分配與運輸的協同價值，而且發現魯棒的兩層規劃具有強烈的穩鍵特征, 同時也發現魯棒的優化過程將有助于增強應急分配過程中的公平程度. 關鍵詞: 應急物資分配；魯棒優化；兩層模型

近年來，世界各地的突發事件頻繁發生，這些大規模的突發性災害事件造成了大量的人員傷亡和巨額的經濟損失. 災害事件發生后，面對急劇增長的物資需求，應急物資的分配與運輸自然成為救援工作中的重要環節. 因此，采用科學的方法從系統性視角探討應急物資分配及運輸的協同決策是合理展開救援行動的一個關鍵問題.

很多學者對相關的問題進行了深入研究. 文獻[1]研究了地震后向多個受災地點分配資源的問題，構建了在時間、資源數量和質量有限的情況下，以死亡人數最小作為目標的動態組合優化模型. 文獻[2]采用模糊規劃的方法探討了災后物資分配的多目標規劃問題. 文獻[3]通過將車輛描述為一種特殊形式的物資形式，把物資分配過程分解為兩個網絡流問題. 文獻[4]針對無法獲取災情詳細數據的情況，構建了一個考慮多種類物資的兩階段多隨機網絡流模型. 文獻[5]考慮了應急物資調度過程中公眾的感知度問題，建立了以最小化公眾風險感知程度和物資未滿足度為目標的混合整數規劃模型. 文獻[6]利用局內決策方法求得了應急物資在兩階段嵌套機制下的有效分配策略. 文獻[7-9]從多個角度對應急系統調度中的多出救點問題展開了研究.

應急物資的分配和運輸具有關聯性和協同性，而大多文獻將這兩個問題作為單獨的主題進行研究，缺少對兩者協同的系統考慮. 非常規突發事件下，需求信息的極度缺失是不可回避的，現有文獻研究主要假定物資需求為常量或需求不確定環境(但事實上假設需求分布信息已知)，沒有有效刻畫需求信息的極度缺失，更沒能體現信息缺失下“底線思維”對應急過程中的決策保障作用. 為此，本文從應急管理者系統決策的特點出發，基于“底線思維”探討非常規災害事件下的應急物資協同分配問題，提出兩層應急物資分配-運輸的優化模型. 模型不僅揭示了分配與運輸的協同價值，而且發現了魯棒的兩層規劃具有強烈的穩健特征，同時發現了魯棒的優化過程將有助于增強應急物資分配過程中的公平程度.

1 應急物資分配-運輸模型

1.1 模型描述及假設

在應急初始響應階段，應急救援決策者通常首先基于對災情的分析和對物資供應量和需求量的估計決定各個災區物資的分配量，之后救援部門根據分配方案，利用可得到的運輸工具將物資盡快運送至災區. 因而，應急物資的分配和運輸是兩個密不可分的救援活動，直接影響了整個救援活動的經濟和時間效果. 以災害事件應對初期的物資分配體系為研究背景，將決策過程轉化為兩個層次的整數規劃模型. 頂層模型從成本最小化的角度確定應急資源的最優配置量，而底層模型從節約時間的角度對頂層的分配方案實施運輸配送，合理規劃車輛的運輸路徑和數量安排，進而及時、有效地實現應急資源分配的協同優化，最大程度地減少災難帶來的損失.

此外，鑒于在救援初期應急決策者只能對受災地區的物資需求情況進行粗略估計，因此納入不確定參數構建魯棒優化分配模型，解決應急物資在需求不確定條件下的物資分配問題. 模型的建立基于以下基本假設：

1) 已知物資供應中心的儲備情況；

2) 從供應中心到受災地區的路況和運輸時間均為定值；

3) 應急中心有權限可以征集足夠的車輛以供物資調度.

1.2 頂層模型(應急物資分配模型)

相關參數設置如下：

1) 參數：I為 物資儲備中心集合，i∈I；J為受災地區集合，j∈J；si為物資儲備中心i的儲備量；rj為對于災區j，未滿足需求的單位懲罰系數；cij為物資儲備中心i到災區j的車輛運輸成本.

2) 決策變量：wij為儲備中心i提供給災區j的物資需求比率；wj為災區j的物資需求未滿足率.

則需求確定情況下的頂層-應急物資分配模型為

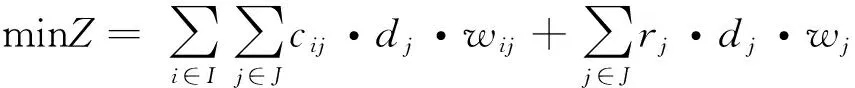
(1)

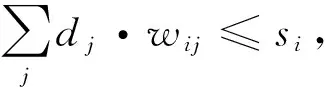
(2)

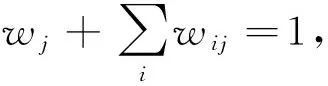
(3)

0≤wj1, ?j∈J;

(4)

0≤wij≤1, ?i∈I,?j∈J.

(5)

目標函數式(1)代表應急物資分配的統籌成本最小化，包含應急物資的運輸成本和受災點物資需求未滿足的懲罰成本；約束式 (2) 表示對所有災區的物資分配總量應少于物資中心i的儲備量；約束式(3) 為災區j的物資需求滿足率與缺乏率之和為1；約束式(4)和式(5)表示決策變量約束.

1.3 底層模型(應急物資運輸模型)

當應急決策者對于物資分配量做出合理決策后，應急施救部門需要考慮物資分配方案在實際情況中的配送效率，即如何依據分配量安排車輛、路徑以盡量減少由于時間的延誤而導致的人員傷亡.

1) 參數：R為由物資儲備中心和災區組成的可行路徑集合；Rij為從物資儲備中心i到災區j之間的可行路徑集合；V為運輸車輛集合；C為車輛的最大運載容量；Ir為路徑r上的物資儲備中心集合；Jr為路徑r上的災區集合；tr為物資在路徑r上的運輸時間.

2) 決策變量：sijrv為車輛v通過路徑r從物資儲備中心i到災區j的運輸數量；brv為車輛v與路徑r的關聯性，若車輛v通過路徑r，brv=1，否則為0.

利用物資分配量作為輸入參數，便得到底層運輸配送模型為

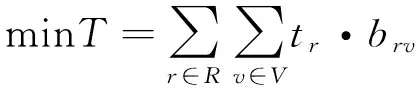
(6)

s.t.

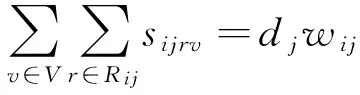
(7)

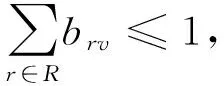
(8)

(9)

brv∈{0,1},sijrv≥0, ?i∈I,?j∈J,

?r∈R, ?v∈V.

(10)

目標函數式(6)代表車輛運輸物資耗費的總時間最小；約束式(7)表示從儲備中心i到災區j的物資運輸總量滿足頂層的物資分配量；約束式(8)表示每部車輛只能通過一條路徑；約束式(9)表示車輛從儲備中心i運輸到災區j的物資總量不得超過該車輛的最大運載能力；約束式(10)規定了決策變量的取值范圍.

2 需求信息有限下的應急物資分配-運輸模型

在緊急救援初期，很難精確預測應急物資的需求量. 為了加強決策的穩健性，從“底線思維”的視角，利用Bertsimas等[10]的魯棒優化理論，將確定性模型轉化為魯棒對應模型，以獲得魯棒優化決策，使物資分配方案不會由于需求的變化而在實際應急物流中失去作用. 相比傳統使用的隨機優化方法，魯棒優化并不需要明確不確定因素的概率分布情況，它以最壞情況下的優化為基礎，確保優化方案對不確定參數的不敏感性. 根據對災害發展和災區的人口情況的統計，物資需求的變動區間為

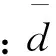
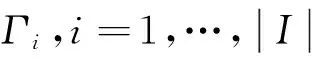
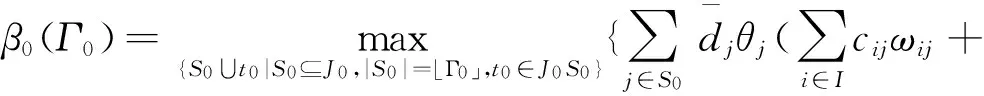
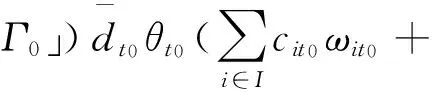
γt0ωt0)},

(11)

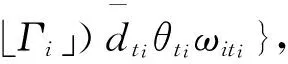
(12)

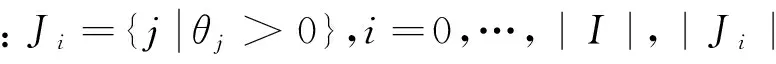
對于式 (11)和式(12)的每個約束，等價于如下的一般形式：

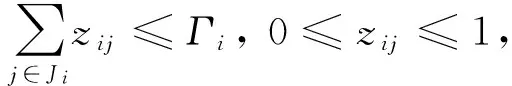
(13)

根據對偶理論，其等價于如下形式：

最終，得到需求不確定條件下的頂層魯棒物資分配模型為

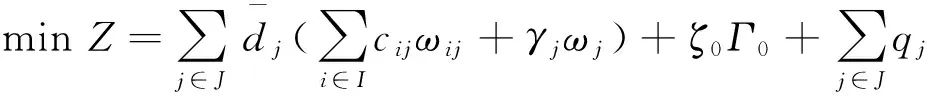
s.t.

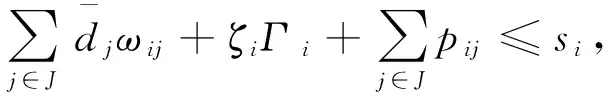
s.t.

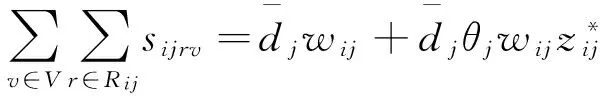
3 數值分析

以某市應急物資調度為背景進行應急物資魯棒分配和運輸配送計劃的有效性以及穩健性的驗證. 共有5個應急物資儲備中心，可能的受災地區有11個. 表1～ 3分別列出了模型的基本參數設置. 假設對于未滿足的需求，懲罰系數為3 000. 所有的運算均通過GAMS軟件在一臺配置為Intel(R) Core(I5) 2 Quad CPU (1.6GHz)，4.0 GB RAM的計算機上進行.

3.1 穩健性分析

為了驗證魯棒模型的穩健性，研究當需求服從均勻分布時，魯棒模型及確定性模型在不同的應急物資需求波動和決策者風險偏好下平均成本與成本標準差的表現. 魯棒模型與確定性模型的成本比較如表4所示. 從表4可以看到，魯棒分配方案的平均成本與需求波動水平和風險規避程度呈現正相關關系，說明魯棒優化方案的穩健性是以經濟性的犧牲為代價. 雖然魯棒分配方案的平均成本高于確定性模型的分配方案，但是前者的成本標準差總低于后者. 因此，當僅獲知需求的區間信息時，決策者采用魯棒優化模型可以實現穩健性較高的分配方案.

表1 物資儲備中心到受災地區的運輸成本

Tab.1 The transportation cost from materials reserve center to affected areas

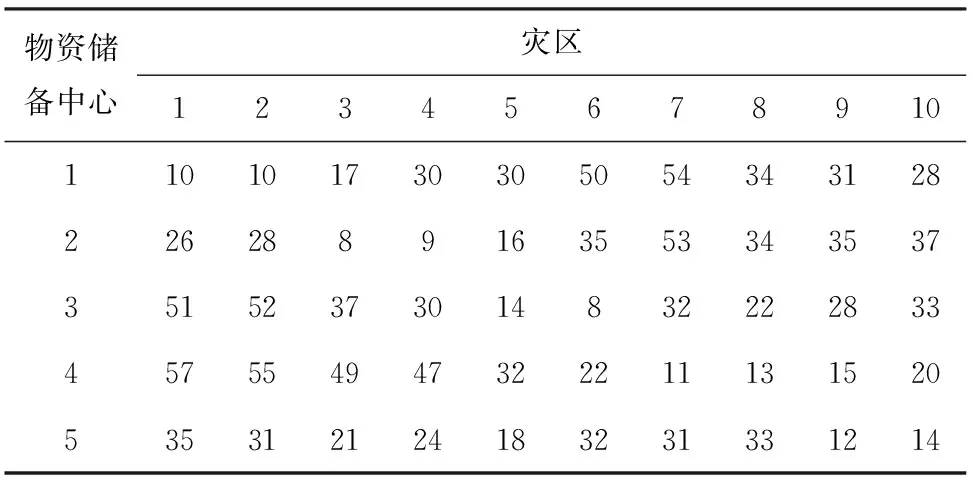
物資儲備中心災區12345678910110101730305054343128226288916355334353735152373014832222833457554947322211131520535312124183231331214

表2 各災區對物資需求數量的名義值

Tab.2 The nominal value of the emergency material in affected areas

災區12345678910需求1500160014001600150015001400130018001400

表3 各個儲備中心的物資供給量

Tab.3 The materials supply in reserve centers

物資儲備中心12345供給25002000300015002000

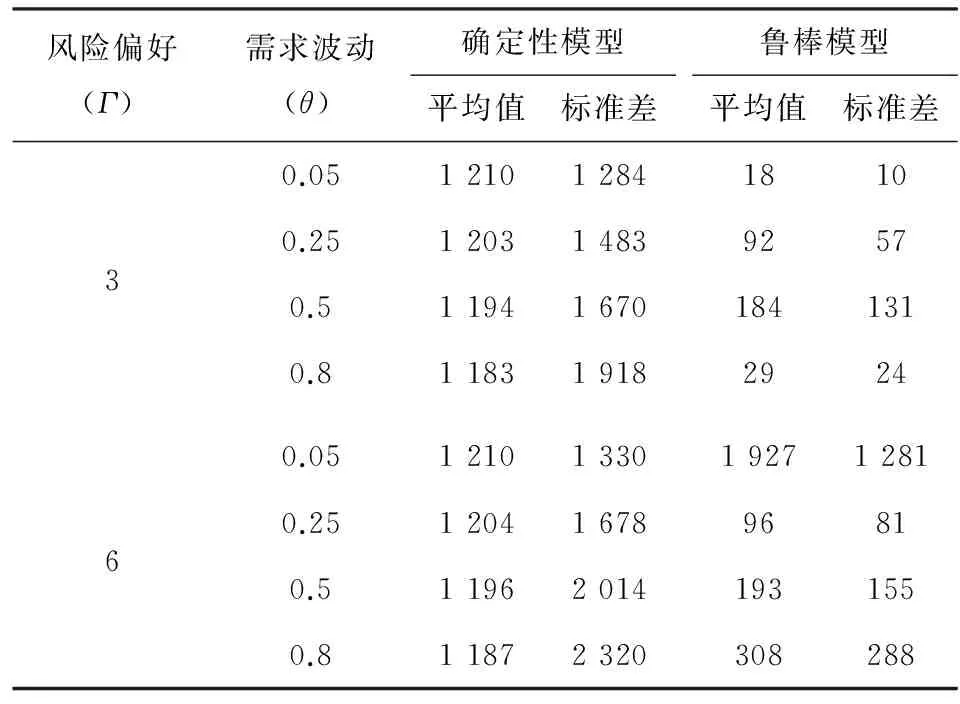
表4 魯棒模型與確定性模型的成本比較Tab.4 The cost of the robust model compared with the deterministic model

注：總成本104

3.2 魯棒運輸方案分析

下面分析與魯棒物資分配決策相匹配的車輛運輸配送計劃，以期為災害發生后實施及時救援提供依據. 假設車輛的最大承載量為1 000，每條路徑以物資儲備中心為出發點，以途經的受災地區順序依次表示，相應的路徑運輸時間如表5所示.

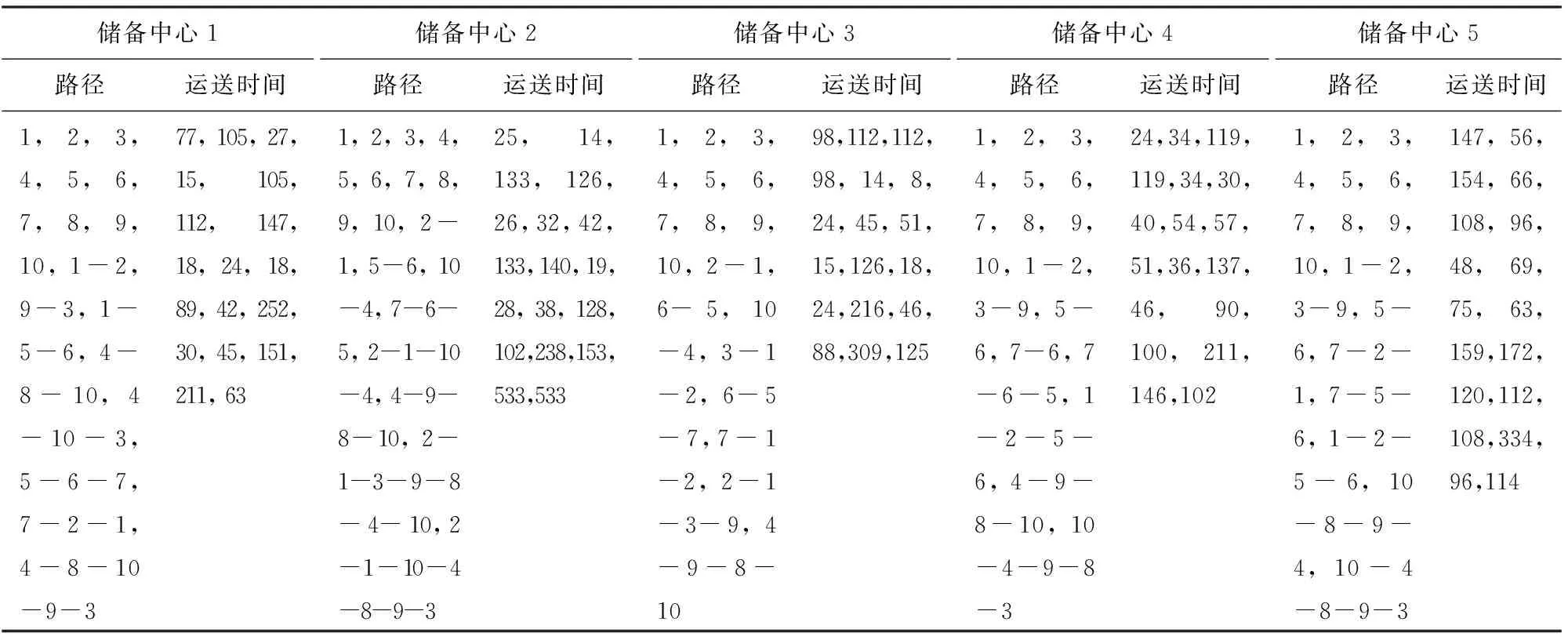
表5 從儲備中心到災區的路徑運輸時間

盡管假設應急部門有權調集足夠多的車輛以供物資調度，但物資運輸模型可以提供一個合理的車輛配置方案滿足最差需求情形下的經濟性和時間性的最優. 若風險偏好Γ=3和需求波動θ=0.05，則如表6所示，每個應急物資儲備中心只需分別安排4, 5, 6 ,4, 3輛運輸車輛即可保證魯棒物資分配方案的順利實施. 此外，儲備中心3安排的車輛數量最多，這與實際中決策者按照供應量最多的物資儲備中心配置最多車輛的經驗判斷是一致的. 從分析方案中的路徑選擇可知，73%的路徑覆蓋多個災區，故保持災區道路之間的良好聯通對于降低物資的運輸配送時間起到了重要作用.

3.3 公平度分析

在分配應急物資時，為了提高受災地區群眾的滿意度，有必要分析分配方案對于災區群眾的公平影響程度. 故定義準則：

即不同災區物資需求滿足率之間的最大差異值.

不同風險偏好和需求波動下的公平度對比如圖1所示. 從圖1可以發現，在其他參數固定的情況下，隨著風險規避程度和需求波動水平的增加，災區間的不公平度也呈現增長的趨勢，說明較小的需求波動和較高的風險偏好可以提高災區對于魯棒應急物資分配決策的滿意度. 相對于確定性模型求得的分配方案的不公平度0.923，在不同風險偏好和需求波動下的魯棒優化模型求得的公平度總是優于前者. 因此，通過對公平指標的分析，可以幫助決策者從平等主義的角度更好地理解魯棒模型的優勢.

表6 物資運輸車輛安排及路徑選擇

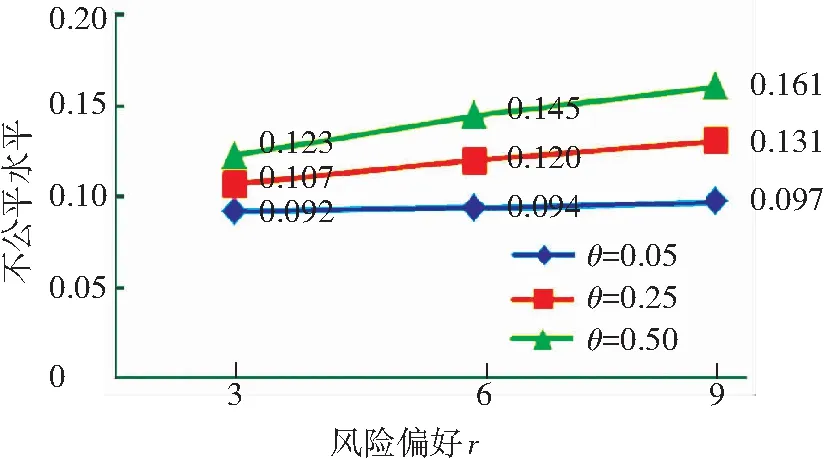
圖1 不同風險偏好和需求波動下的公平度對比

Fig.1 The fair degree under demand fluctuations and different risk attitude

4 結論與展望

1) 在應急資源的協同管理中，基于分解技術支持的應急物資分配與運輸的協同過程具有積極價值.

2) 在信息極度缺失下，體現“底線思維”應急決策過程的魯棒優化決策具有非常強的穩健特征.

3)魯棒的兩階段協同優化過程不僅有助于提高應急資源使用效率和運輸車輛科學規劃，同時非常具有實用價值的是，它能提升應急物資分配過程中的“公平性”.

雖然本文的研究發現了基于“底線思維”的魯棒兩階段協同規劃模型的應急價值，但事實上，應急管理過程中(特別是非常規突發事件應急過程中)應急物資供應以及應急運輸過程中也蘊涵著極大的不確定性，如何使“底線思維”的魯棒模型包括更多的不確性信息是一項極具挑戰性的科學任務，需要深入的科學探索. 欣喜的是，魯棒方法已經引起了應急管理學者的重視，進一步的研究可參考文獻[11-12]展開.

[1] FIEDRICHF, GEHBAUER F ,RICKERS U. Optimized resource allocation for emergency response after earthquake disasters[J]. Safety Science,2000,35(1-3): 41-57.

[2] TZENG G H, CHENG H J ,HUANG T D. Multi-objective optimal planning for designing relief delivery systems[J]. Transportation Research Part E: Logistics and Transportation Review,2007,43(6): 673-686.

[3] ?ZDAMAR L, EKINCI E,Kü?üKYAZICI B. Emergency logistics planning in natural disasters[J]. Annals of Operations Research,2004,129(1-4): 217-245.

[4] BARBAROSOGLU G, ?ZDAMAR L, ?EVIK A. An interactive approach for hierarchical analysis of helicopter logistics in disaster relief operations[J]. European Journal of Operational Research,2002,140(1): 118-133.

[5]王旭坪, 馬超 ,阮俊虎. 考慮公眾心理風險感知的應急物資優化調度[J]. 系統工程理論與實踐, 2013, 33(7): 1735-1742.

WANG X，MA C，RUAN J. Emergency supplies optimal scheduling considering the public’s psychological risk perception[J]. Systems Engineering: Theory & Practice, 2013,33(7):1735-1742.

[6]于輝 , 劉洋. 應急物資的兩階段局內分配策略[J]. 系統工程理論與實踐, 2011,31(3): 394-403.

YU H, LIU Y. Two-stage online distribution strategy of emergency material[J]. Systems Engineering Theory & Practice, 2011,31(3):394-403.

[7]劉春林, 盛昭瀚,何建敏. 基于連續消耗應急系統的多出救點選擇問題[J]. 管理工程學報,1999, 13(3):13-16.

LIU C, SHENG Z, HE J. Multi-depot selection problem based on the continuous consumption emergency system[J]. Journal of Industrial Engineering and Engineering Management, 1999,13(3):13-16.

[8]劉春林, 何建敏 , 盛昭瀚. 多出救點應急系統最優方案的選取[J]. 管理工程學報,2000, 14(1):13-15.

LIU C, HE J, SHENG Z. Selection of optimal scheme for multi-depot emergency systems[J]. Journal of Industrial Engineering and Engineering Management, 2000,14(1):13-15.

[9]劉春林, 何建敏,施建軍. 一類應急物資調度的優化模型研究[J]. 中國管理科學,2001,9(3): 29-36.

LIU C, HE J, SHI J. The study on optimal model for a kind of emergency material dispatch Problem[J]. Chinese Journal of Management Science, 2001,9(3):29-36.

[10]BERTSIMAS D, SIM M. The price of robustness[J]. Operations Research,2004,52(1): 35-53.

[11]BERTSIMAS D, SIM M. Robust discrete optimization and network flows[J]. Mathematical Programming,2003,98(1/2/3): 49-71.

[12]BEN-TAL A, NEMIROVSKI A. Robust optimization-methodology and applications[J]. Mathematical Programming,2002,92(3): 453-480.

(編輯 王小唯 苗秀芝)

Two-level robust optimization model of emergency relief distribution-transportation from the baseline perspective

YU Hui , QU Yaping

(College of Economics and Business Management, Chongqing University, Chongqing 400044, China)

The unconventional emergency needs to be dealt with from the perspective of baseline. That is, we need to study problems based on the worst scenario. Thus, the paper formulated a two-level robust optimization model to solve the coordination problem arising from the relief distribution and transportation. The topline model determines the optimal distribution of emergency resource from the perspective of cost minimization, while the baseline model is to transport and distribute based on the distribution policy of topline from the perspective of time saving, in order to realize the coordinate optimization of emergency resource allocation timely and efficiently, and reduce most the loss of disaster. The model described the scarcity of relief demand and converted the coordination problem into two connected problems. Finally, the numerical analysis demonstrated the coordination value and robustness of the distribution policy. Besides, robust approach helps improve the equity of distribution plan.

emergency relief distribution; robust optimization; two-level model

10.11918/j.issn.0367-6234.2016.11.028

2015-06-10

中央高校基本科研業務費項目(CDJKXB14004)

于 輝(1973—)，男，教授，博士生導師

于 輝, yuhui@cqu.edu.cn

F251.2

A

0367-6234(2016)11-0178-05