基于廣義高斯分布的貝葉斯概率矩陣分解方法
燕彩蓉 張青龍 趙 雪 黃永鋒
(東華大學計算機科學與技術學院 上海 201620)(cryan@dhu.edu.cn)
?
基于廣義高斯分布的貝葉斯概率矩陣分解方法
燕彩蓉 張青龍 趙 雪 黃永鋒
(東華大學計算機科學與技術學院 上海 201620)(cryan@dhu.edu.cn)
貝葉斯概率矩陣分解方法因較高的預測準確度和良好的可擴展性,常用于個性化推薦系統,但其推薦精度會受初始評分矩陣稀疏特性的影響.提出一種基于廣義高斯分布的貝葉斯概率矩陣分解方法GBPMF(generalized Gaussian distribution Bayesian PMF),采用廣義高斯分布作為先驗分布,通過機器學習自動選擇最優的模型參數,并基于Gibbs采樣進行高效訓練,從而有效緩解矩陣的稀疏性,減小預測誤差.同時考慮到評分時差因素對預測過程的影響,在采樣算法中添加時間因子,進一步對方法進行優化,提高預測精度.實驗結果表明:GBPMF方法及其優化方法GBPMF-T對非稀疏矩陣和稀疏矩陣均具有較高的精度,后者精度更高.當矩陣非常稀疏時,傳統貝葉斯概率矩陣分解方法的精度急劇降低,而該方法則具有較好的穩定性.
個性化推薦系統;貝葉斯概率矩陣分解;機器學習;廣義高斯分布;稀疏矩陣
推薦系統作為一種有效的信息過濾手段,是當前解決信息過載問題及實現個性化信息服務的有效方法之一[1].近幾年舉辦的比賽,如Netflix百萬美金大獎賽、KDD CUP 2011音樂推薦比賽、百度電影推薦競賽以及阿里巴巴大數據競賽更是把推薦系統的研究推向了高潮.
作為協同過濾推薦系統中的一種新型推薦生成方法,基于矩陣分解(matrix factorization, MF)的潛在因子模型(latent factor model)因準確度高、可擴展性好等因素受到了廣泛的關注[2].常用的矩陣分解方法主要包括規范化的SVD(regularized SVD)[3]、非負矩陣分解(nonnegative matrix factorization, NMF)[4]、概率矩陣分解(probabilistic matrix fact-orization, PMF)[5]和貝葉斯概率矩陣分解(Bayesian PMF)[6]等.其中Bayesian PMF從概率的角度探討矩陣分解的最優化問題,算法的預測準確性比較高,且不需要設定正則化系數,因此得到了廣泛應用[7].
現實生活中,數據矩陣往往極其稀疏,以最近熱映的電影《魔獸》為例,中國票房14.7億元,觀影人次近4 000萬,豆瓣評分人次為129 888,評分密度僅為0.325%.為了緩解數據稀疏問題,學者們提出了社會化推薦(social recommendation)方法[8-9].為了提取更優的潛在特征向量,文獻[10]將用戶的各種社會網絡關系融合到矩陣的優化分解過程中,提出社會化矩陣分解;文獻[11]提出因子分解機(factorization machines)模型.然而,用戶對項目的評分信息與用戶之間的社會關系網絡信息往往來源于不同的數據源,因此社會化推薦在推廣應用中有一定的局限性[12].
針對矩陣稀疏性影響預測精度的問題,本文在貝葉斯概率矩陣分解的基礎上,提出一種基于廣義高斯分布的貝葉斯概率分解方法,同時考慮用戶評價行為對用戶評分的影響會隨著時間弱化的情況[13],在方法中添加時間因子,進一步提高預測精度.
1 相關定義
推薦系統中最基本的數據就是關于用戶對項目的評分,通過對它們進行分析,了解用戶與項目之間的關聯,從而實現項目推薦.
定義1. 評分矩陣.假設有用戶向量u(大小為n)、項目向量v(大小為m),每個用戶對每個項目都可能產生一個評分,其值構成了用戶-項目評分矩陣Rn×m.
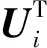
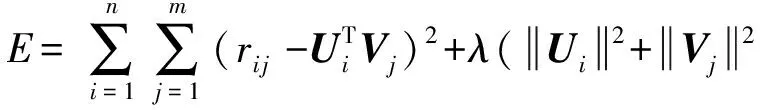
(1)
通常采用隨機梯度下降(stochastic gradient descent, SGD)方法優化目標損失函數,當其取最小值時對應的Un×k和Vk×m即為最優解.
定義3. 稀疏矩陣.指矩陣中非零元素占全部元素的百分比很小的矩陣(通常設為5%以下).實際應用中,由于多數用戶不會對其所瀏覽的所有項目做出顯式反饋,因此評分矩陣通常是稀疏的.本文主要研究稀疏矩陣的分解.
定義4. 貝葉斯概率矩陣分解.假設用戶特征向量矩陣Un×k和項目特征向量矩陣Vk×m服從均值為μU,μV,方差為ΛU,ΛV的高斯分布,用戶、項目特征向量矩陣的條件概率分布如下:
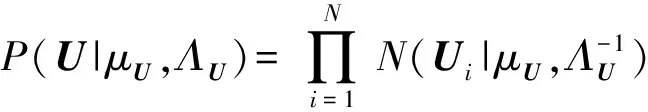
(2)
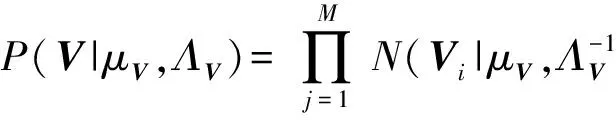
(3)
用戶對項目的評分變成一個概率問題:
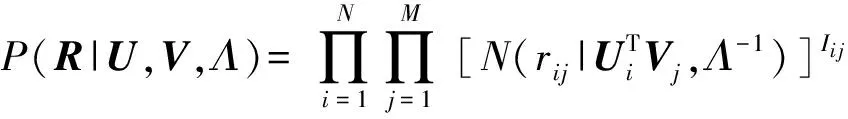
(4)
其中,N(x|μ,Λ-1)是期望為μ、方差為Λ-1的高斯分布,Iij是示性函數;若rij≠0,則Iij=1,否則Iij=0.Bayesian PMF進一步設定ΘU={μU,ΛU},ΘV={μV,ΛV}的先驗分布為高斯-威沙特分布(Gaussian-Wishart distribution),將參數{ΛU,ΛV}整合到算法內部,概率調整為
P(ΘU|Θ0)=P(μU|ΛU)P(ΛU)=
N(μU|μ0,(β0ΛU)-1)W(ΛU|ω0,ν0),
(5)
P(ΘV|Θ0)=P(μV|ΛV)P(ΛV)=
N(μV|μ0,(β0ΛV)-1)W(ΛV|ω0,ν0),
(6)
其中:
1)Θ0={μ0,ν0,ω0,Λ,β0};
2)W(Λν|ω0,ν0)是自由度為v0、尺度參數為ω0的威沙特分布.
貝葉斯推斷是將先驗的思想和樣本數據相結合得到后驗分布,然后根據后驗分布進行統計推斷,其精度受樣本數量及其先驗分布準確性的影響.Bayesian PMF采用高斯分布作為先驗分布,對數據比較敏感,當評分矩陣中非零元素較少時,這種方法具有較高的精度,但當評分矩陣非常稀疏時,很難斷定樣本分布服從高斯分布,其推薦效果不理想[6].本文針對評分矩陣稀疏性不確定問題,提出采用適用范圍更加寬泛的廣義高斯分布作為先驗分布來緩解數據的稀疏問題,提高推薦精度.
Bayesian PMF采用Markov鏈蒙特卡羅算法(Markov chain Monte Carlo, MCMC)進行訓練,該算法具有較低的算法復雜度和較高的檢測性能,目前在MCMC方法中最常用的是Gibbs采樣(Gibbs sampling)算法.因此,本文在訓練基于廣義高斯分布的貝葉斯概率矩陣分解方法GBPMF(generalized Gaussian distribution Bayesian PMF)的過程中,使用Gibbs采樣算法進行貝葉斯推斷.
2 基于廣義高斯分布的貝葉斯概率矩陣分解
2.1 廣義高斯分布對稀疏數據的影響
廣義高斯分布(generalized Gaussian distribution, GGD)的密度函數(probability density function)是廣義伽瑪分布的密度函數的推廣形式,其密度函數定義為[14]
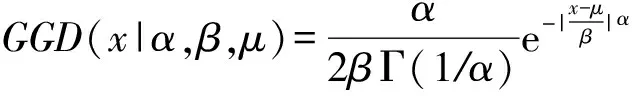
(7)
其中:
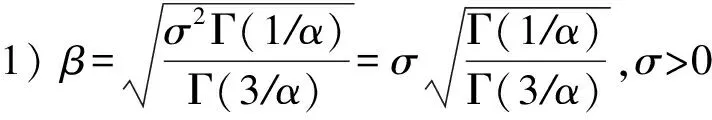
3) 參數μ,σ2,α,β分別稱為GGD的均值、方差、形狀參數和尺度參數.
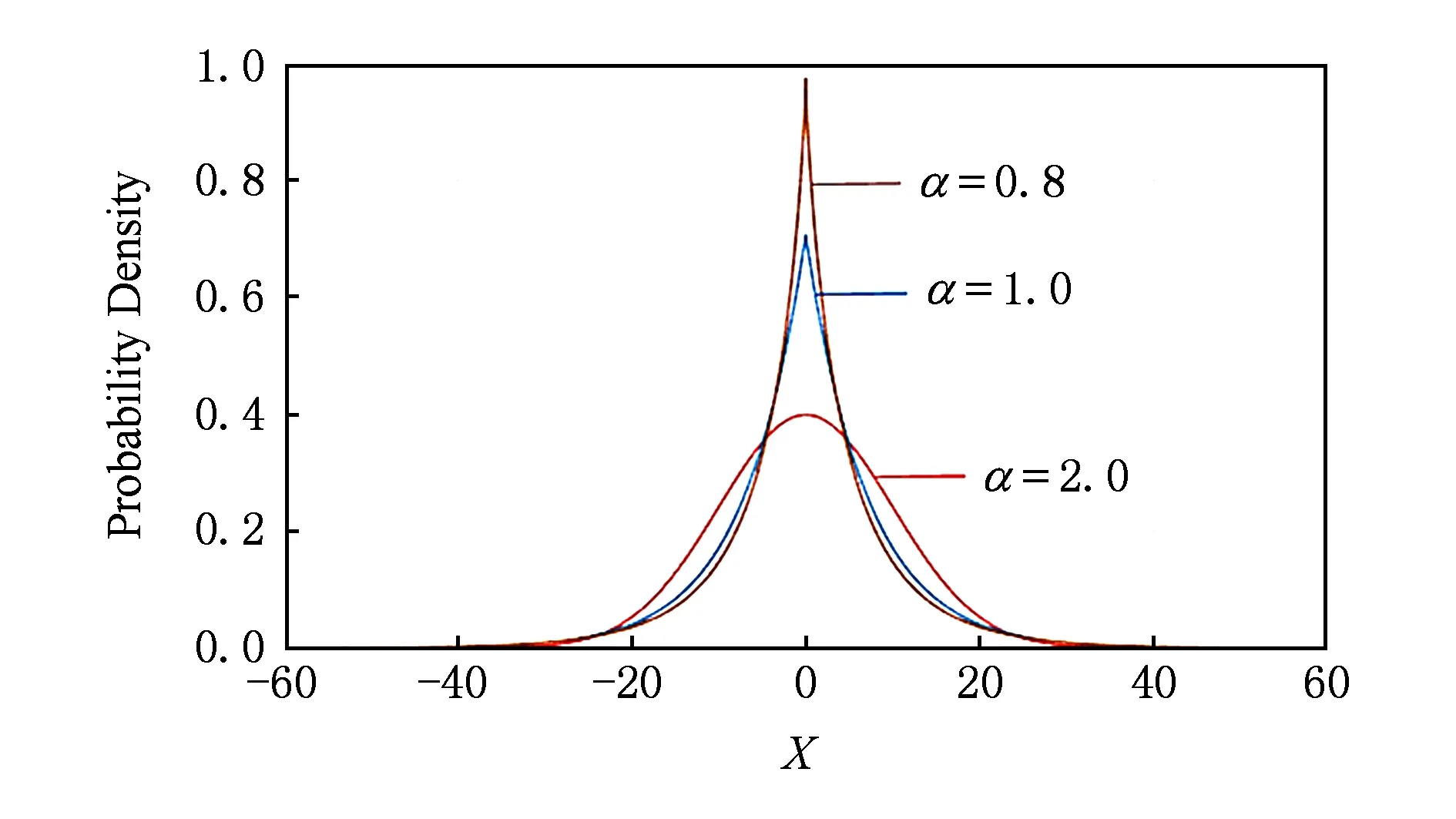
Fig. 1 Probability density comparison of GGD.圖1 GGD概率密度變化示例
圖1所示為μ=0,σ2=10,α分別為2.0,1.0,0.8的GGD概率密度圖.其中縱坐標表示樣本的概率分布密度,0點處縱坐標值越大表示樣本取0值時的概率密度越大,即樣本的稀疏性越大.通過圖1所示,我們可以看出:樣本的稀疏率與α值呈負相關,即α值越小時,GGD在0附近有越高的峰值;當α=2.0時GGD為高斯分布,我們可以通過調節α值來有效緩解數據的稀疏性.同時,相對于高斯分布,GGD在數據兩側出現的概率較大,這有助于提高推薦系統對項目長尾特性的發掘能力.
針對稀疏矩陣導致推薦結果誤差較大的問題,本文提出一種改進的貝葉斯概率矩陣分解方法GBPMF,采用GGD作為用戶-項目特征向量矩陣的先驗分布來有效緩解矩陣稀疏性.
2.2 GBPMF方法
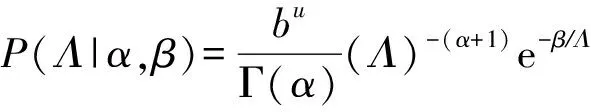
(8)
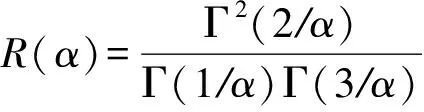
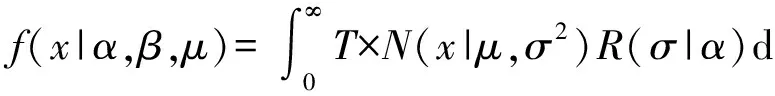
(9)
GBPMF方法的評分矩陣預測過程如下:
1) 根據GGD得到用戶特征向量Ui和項目特征向量Vj;
2) 根據逆伽馬分布計算高斯分布的方差Λ;
Gibbs采樣是一種典型的MCMC算法,適用于聯合概率未知,條件概率容易獲取的情況.GBPMF方法在訓練過程中,采用Gibbs采樣進行貝葉斯推斷,即利用條件概率構造平穩分布為所求聯合概率的Markov鏈,進行K次抽樣,此時的樣本{U,V}可近似認為是來自聯合概率P(U,V|R,αU,βU,αV,βV)的抽樣,最后利用式(10)進行評分預測:

(10)
Gibbs采樣的具體過程可以描述為:
1) 對參數Ui進行采樣,提取出與之相關的所有變量,利用貝葉斯公式,可得:
P(Ui|R,V,Λ,(αU)i,(βU)i)∝
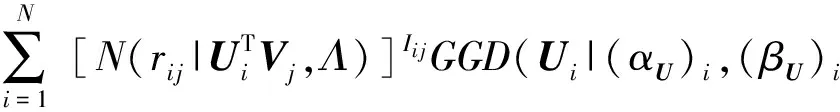
(11)
令P((λU)ki|(αU)ki,(βU)ki)=R((λU)ki|(αU)ki),則有
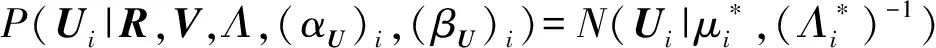
(12)
其中:
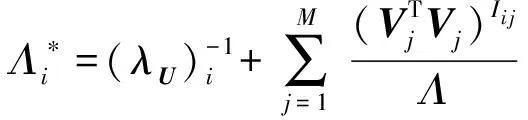
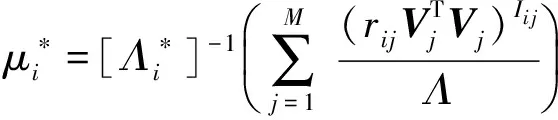
2) 對超參數(λU)i,(αU)i采樣,根據貝葉斯公式,可得:
P((λU)i|Ui,(αU)i)∝P(Ui|(λU)i,(αU)i)P((λU)i).
(13)
根據指數函數的性質,可以得到(λU)i服從逆高斯分布(inverse Gauss distribution)
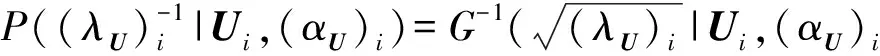
(14)
對廣義高斯分布的形狀參數(αU)i,它的條件概率滿足廣義逆高斯分布
P((αU)i|Ui,(λU))=GIG(γ+1,(λU)i+a,b),
(15)
其中,a,b為常數,本文為了計算方便,取γ=0.5將廣義逆高斯分布簡化為逆高斯分布.
U和V具有對稱性,采樣具有相同的形式.
3) 對參數Λ進行采樣.參數Λ的條件概率形式為
P(Λ|R,U,V)=Γ-1(aΛ,bΛ),
(16)
其中:
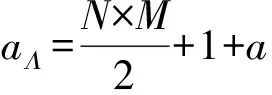
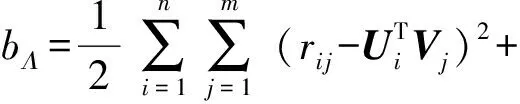
GBPMF的Gibbs采樣算法見算法1所示.
算法1. GBPMF的Gibbs采樣算法.
輸入: 原始評分矩陣R、采樣數目K、迭代次數D;
輸出:K個樣本點.
① 初始化算法參數(U1,V1);
② for每一個采樣點do
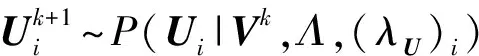
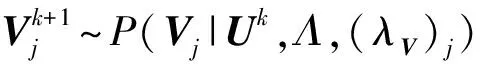
⑤ 根據式Λ~P(Λ|R,U,V)對參數Λ進行采樣;
⑥ end for
⑦ 返回K個采樣點(U1,V1),(U2,V2),…,(Uk,Vk).
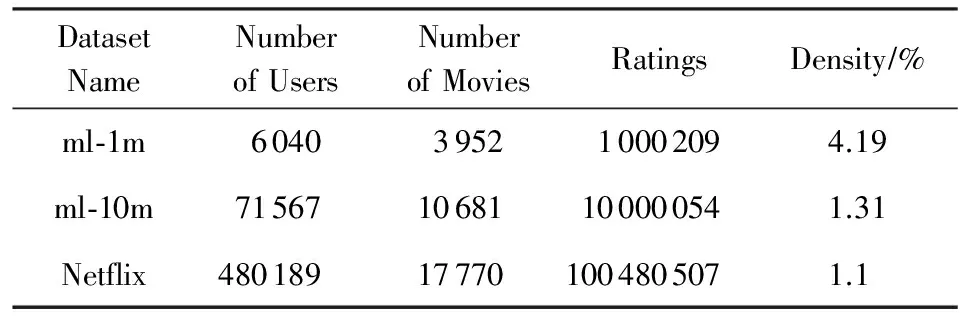
每次Gibbs采樣的時間為K×max(m,n),假設迭代D次,則采樣時間為D×K×max(m,n);又矩陣分解的運行時間是F×S×p,其中F為用戶對物品的評分記錄數,p為分解維度,S為迭代次數[16].故整個模型的運行時間為D×K×max(m,n)+F×S×p.通常情況下,D×K×max(m,n) GBPMF方法在處理時不考慮評分產生的時間因素.實際應用中,評分產生的時間因素能夠反映用戶的行為變化,因而對預測有較大影響.這點在已有的矩陣分解模型中沒有考慮到.本文通過在采樣算法中添加評分時差因素來進行調優,優化后的方法簡稱為GBPMF-T,處理過程如下: 1) 為GBPMF模型添加偏置項: bij=μ+bi+bj, (17) 2) 參考文獻[17]建立鄰域模型,此時預測評分為 (18) 3) 為了提高推薦準確率,對權重矩陣進行0-1標準化,即: (19) 文獻[18]已經證明,對權重矩陣標準化處理可以有效提高評分預測準確率. 4) 將評分時差融入到基于領域的算法中,修正相關參數,建立算法為 (20) 其中,Δt=tij-til表示用戶i對項目j和項目l的評分時差;f(ωj l,Δt)是一個考慮了時間衰減后的相似度函數,它的主要目的是建立用戶行為與評分時差的函數,提高用戶最近行為在推薦系統中的權重. 5) 定義f為 (21) 6) 加入時間信息后的目標損失函數為 (22) 其中,λ2是為防止過擬合添加的正則化參數. (23) 同樣我們可以用Gibbs采樣對GBPMF-T方法進行貝葉斯推斷.此時,K次抽樣時的樣本{U,V,X,Y}可認為是來自聯合概率P(U,V,X,Y|R,αU,βU,αV,βV,αX,βX,αY,βY)的抽樣,其近似計算為 (24) 由于X,Y和U,V類似,可以按式(12)進行采樣.此時參數Λ的條件概率形式為 P(Λ|R,U,V,X,Y)=Γ-1(aΛ,bΛ), (25) 其中: GBPMF-T的Gibbs采樣算法見算法2所示. 算法2. GBPMF-T的Gibbs采樣算法. 輸入: 原始評分矩陣R、時間矩陣T、數目K、迭代次數D; 輸出:K個樣本點. ① 初始化算法參數(U1,V1,X1,Y1); ② for每一個采樣點do ⑦ 根據式Λ~P(Λ|R,U,V,X,Y)對參數Λ進行采樣; ⑧ end for ⑨ 返回K個采樣點(U1,V1,X1,Y1),(U2,V2,X2,Y2),…,(Uk,Vk,Xk,Yk). 整個模型的時間復雜度為O(F×S×p),這和Bayesian PMF方法的時間復雜度一樣. 4.1 數據集和評價標準 實驗采用ml-1m數據集、ml-10m數據集和Netflix數據集作為測試數據集來檢驗GBPMF和GBPMF-T方法的預測精度.MovieLens數據集為用戶對自己看過的電影進行評分的數據集,評分分值為1~5.MovieLens數據集包括2個不同大小的庫,小規模的庫ml-1m數據集是6 040個用戶對3 900部電影的大約100萬次評分;大規模的庫ml-10m數據集是71 567個用戶對10 681部電影的大約1 000萬次評分的數據.Netflix數據集來自于電影租賃網Netflix的數據庫,包含了480 189個匿名用戶對大約17 770部電影作出的大約1億次評分.3個數據集的統計信息如表1所示: Table 1 Information of the Datasets 實驗使用的主要評價標準是在推薦預測系統中常用的均方根誤差(root mean square error,RMSE)和平均絕對誤差(mean absolute error,MAE).RMSE,MAE值越小,表示算法性能越好.RMSE定義為 (26) MAE采用絕對值計算預測誤差,定義為 (27) 本文設計了3組實驗對經典Bayesian PMF,GBPMF,GBPMF-T性能進行對比. 實驗運行硬件平臺為Inter?CoreTMi5-4460 CPU @ 3.20 GHz、15.6 GB內存、976 GB硬盤、64位Ubuntu 15.1操作系統,編譯軟件為IntelliJ IDEA,算法編程語言為Python. 4.2 實驗結果與分析 實驗分別將ml-1m數據集、ml-10m數據集和Netflix數據集,按照9∶1的比率隨機劃分為訓練集和測試集,實驗運行10次,結果取平均值.考慮到時間和精度問題,經過多次實驗,我們設置學習速率為0.05,初始化正則參數為0.01. 由于整個實驗所采用的3個影響因子相互獨立,在實驗設計時,我們主要考慮單個因子對實驗結果的影響. A組實驗考慮Gibbs采樣迭代次數對實驗結果的影響,選取ml-1m數據集測試,依次增大Gibbs采樣迭代次數,直到Bayesian PMF和GBPMF測試的MAE值趨于收斂.不失一般性,實驗選取矩陣分解特征維數為10,實驗結果如圖2所示: Fig. 2 MAE comparison on Gibbs iterations.圖2 Gibbs采樣次數對性能的影響 從圖2中可以看出,相對于Bayesian PMF,GBPMF進行Gibbs采樣,MAE值趨于穩定,需要的迭代次數更少.通過第2節對Gibbs采樣算法時間復雜度的分析可知,Gibbs采樣耗時與迭代次數成正相關.可見,相對于經典Bayesian PMF,GBPMF在運行時間上具有一定的優勢. 我們設計B組實驗測試矩陣分解特征維數對模型性能的影響.實驗選取3種不同的數據集,以RMSE值作為最終測評標準,其中Gibbs采樣迭代次數取50,實驗結果如圖3,4所示: Fig. 3 RMSE comparison on ml-1m.圖3 ml-1m的RMSE值比較 Fig. 4 RMSE comparison on Netflix.圖4 Netflix的RMSE值比較 從圖3,4中可以看出,在ml-1m數據集上,與經典Bayesian PMF相比,GBPMF的預測精度提高了1.02%,GBPMF-T的預測精度提高了4.25%;在Netflix數據集上,與經典Bayesian PMF相比,GBPMF的預測精度提高了多少3.83%,GBPMF-T的預測精度提高了6.78%,可見評分時差和偏置因素對推薦系統預測精度的影響很大.另外,由于Netflix數據集的評分密度只有1.1%,小于ml-1m數據集的評分密度(4.19%),我們大膽推測,在數據稀疏的條件下,GBPMF和GBPMF-T算法能夠獲得更高的精度. 為了驗證上述推測,我們只考慮矩陣稀疏性對推薦精度的影響,進行C組實驗,利用ml-10m數據集生成評分密度小于1%的測試環境(設定用戶對電影評分數量的閾值為num_m.若用戶評分記錄數量小于num_m,評分記錄取實際評分數量;若用戶評分數量大于num_m,隨機抽取num_m條評分記錄).實際應用中的評分密度一般都小于1%,稀疏矩陣可以更好地反映算法提取潛在特征的能力.實驗結果如圖5所示. Fig. 5 RMSE comparison on sparse matrix.圖5 稀疏矩陣的RMSE值比較 從圖5中可以看出,在稀疏數據集上(數據稀疏率為0.96%),與經典Bayesian PMF相比,GBPMF的預測精度提高了4.03%,且2種算法在矩陣分解特征維數為16的時候都已經收斂. 在實際的推薦系統中,數據的稀疏性往往小于1%,為了更直觀地顯示數據的稀疏性,我們設計了D組實驗,選擇矩陣分解特征維數為16,通過調節num_m的值改變數據集的稀疏性,實驗結果如圖6所示: Fig. 6 Influence of matrix sparsity on two methods.圖6 矩陣稀疏性對Bayesian PMF和GBPMF的影響 通過圖6可以看出,隨著評分密度的減小,Bayesian PMF和GBPMF的預測精度都在迅速減小,但GBPMF預測精度減小的幅度要小于Bayesian PMF.值得注意的是,當矩陣極其稀疏(<0.5%)時,GBPMF預測精度要遠好于Bayesian PMF,從而說明GBPMF能夠有效緩解矩陣稀疏性問題. 本文針對稀疏評分矩陣會降低推薦精度的問題,提出基于廣義高斯分布的貝葉斯概率矩陣分解方法GBPMF.方法采用廣義高斯分布作為先驗分布,通過調節參數值來有效緩解數據的稀疏性,也有助于提高推薦系統對項目長尾的發掘能力;在方法訓練過程中,使用Gibbs采樣進行貝葉斯推斷,適用于聯合概率未知,條件概率容易獲取的情況;最后通過添加評分時差因子對方法進行優化,進一步提高方法的精度.實驗表明:在數據稀疏的情況下,方法仍能保持較高的精度,從而有效提高推薦系統的預測準確率. 在未來的研究中,我們將有效挖掘用戶和項目的屬性以及屬性之間的關系,從而確定有用的隱含特征,進一步提高矩陣分解方法的精度. [1]Goldberg D, Nichols D, Oki B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35(12): 61-70 [2]Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30-37 [3]Billsus D, Pazzani M J. Learning collaborative information filters[C] //Proc of the 4th Int Conf on Machine Learning. New York: ACM, 1998: 46-54 [4]Lee D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-91 [5]Mnih A, Salakhutdinov R. Probabilistic matrix factorization[C] //Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 880-887 [6]Salakhutdinov R. Bayesian probabilistic matrix factorization using MCMC[C] //Proc of the 25th Int Conf on Machine Learning. New York: ACM, 2008: 880-887 [7]Fang Yaoning, Guo Yunfei, Lan Julong. A Bayesian probabilistic matrix factorization algorithm based on logistic function[J]. Journal of Electronics & Information Technology, 2014(3): 715-720 (in Chinese)(方耀寧, 郭云飛, 蘭巨龍. 基于Logistic函數的貝葉斯概率矩陣分解算法[J]. 電子與信息學報, 2014(3): 715-720) [8]Wang Zhi, Sun Lifeng, Zhu Wenwu, et al. Joint social and content recommendation for user-generated videos in online social network[J]. IEEE Trans on Multimedia, 2013, 15(3): 698-709 [9]Quijano-Sanchez L, Recio-Garcia J A, Diaz-Agudo B, et al. Social factors in group recommender systems[J]. ACM Trans on Intelligent Systems & Technology, 2013, 4(1): 1199-1221 [10]Jamali M, Ester M. A transitivity aware matrix factorization model for recommendation in social networks[C] //Proc of the 22nd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2011: 2644-2649 [11]Rendle S. Factorization machines[C] //Proc of the 10th IEEE Int Conf on Data Mining. New York: ACM, 2010: 995-1000 [12]Meng Xiangwu, Liu Shudong, Zhang Yujie, et al. Research on social recommender systems[J]. Journal of Software, 2015, 26(6): 1356-1372 (in Chinese)(孟祥武, 劉樹棟, 張玉潔, 等. 社會化推薦系統研究[J]. 軟件學報, 2015, 26(6): 1356-1372) [13]Koren Y. Collaborative filtering with temporal dynamics[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 89-97 [14]Miller J, Thomas J. Detectors for discrete-time signals in non-Gaussian noise[J]. IEEE Trans on Information Theory, 1972, 18(2): 241-250 [15]Wang Taiyue, Li Zhiming. A fast parameter estimation of generalized Gaussian distribution[J]. Chinese Journal of Engineering Geophysics, 2006, 3(3): 172-176 (in Chinese)(汪太月, 李志明. 一種廣義高斯分布的參數快速估計法[J]. 工程地球物理學報, 2006, 3(3): 172-176) [16]Xiang Liang. Recommended System Practice[M]. Beijing: Posts & Telecom Press, 1998 (in Chinese)(項亮. 推薦系統實踐[M]. 北京: 人民郵電出版社, 2012: 72-73) [17]Koren Y. Factor in the neighbors: Scalable and accurate collaborative filtering[J]. ACM Trans on Knowledge Discovery from Data, 2010, 4(1): 1-24 [18]Karypis G. Evaluation of item-based Top-N, recommenda-tion algorithms[C] //Proc of the 10th Int Conf on Information and Knowledge Management. New York: ACM, 2001: 247-254 Yan Cairong, born in 1978. PhD of Xi’an Jiaotong University. Associate professor and MS supervisor. Member of China Computer Federation. Her main research interests include parallel computing, distributed system and big data analyzing. Zhang Qianglong, born in 1990. MSc. His main research interests include concentrate on personalized recommender, data mining and deep learning. Zhao Xue, born in 1992. MSc. Her main research interests include concentrate on social network analyzing and data mining. Huang Yongfeng, born in 1971. PhD of Shanghai Jiaotong University. Associate professor and MS supervisor. His main research interests include pattern recognition, Internet of things and big data analyzing. A Method of Bayesian Probabilistic Matrix Factorization Based on Generalized Gaussian Distribution Yan Cairong, Zhang Qinglong, Zhao Xue, and Huang Yongfeng (School of Computer Science and Technology, Donghua University, Shanghai 201620) The method of Bayesian probability matrix factorization (Bayesian PMF) is widely used in the personalized recommendation systems due to its high prediction accuracy and excellent scalability. However, the accuracy is affected greatly by the sparsity of the initial scoring matrix. A new Bayesian PMF method based on generalized Gaussian distribution called GBPMF is proposed in this paper. In the method, the generalized Gaussian distribution (GGD) is adopted as the prior distribution model in which some related parameters are adjusted automatically through machine learning to achieve desired effect. Meanwhile, we apply the Gibbs sampling algorithm to optimize the loss function. Considering the influence of the time difference of scoring in the prediction process, a temporal factor is integrated into the sampling algorithm to optimize the method and improve its prediction accuracy. The experimental results show that our methods GBPMF and GBPMF-T can obtain higher accuracy when dealing with both sparse matrix and non-sparse matrix, and the latter can even get better effect. When the matrix is very sparse, the accuracy of Bayesian PMF decreases sharply while our methods show stable performance. personalized recommender systems; Bayesian PMF; machine learning; generalized Gaussian distribution (GGD); sparse matrix 2016-08-15; 2016-10-25 國家自然科學基金項目(61402100);中央高校基本科研業務費專項資金(16D111210) This work was supported by the National Natural Science Foundation of China (61402100) and the Fundamental Research Funds for the Central Universities of China (16D111210). TP3913 基于評分時差的GBPMF方法優化
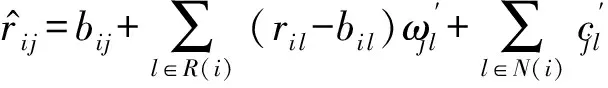
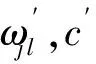
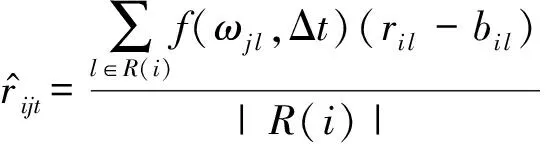
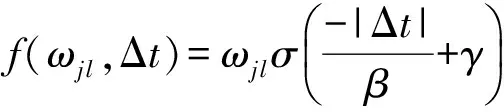
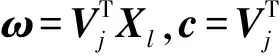
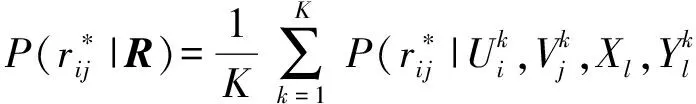
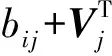
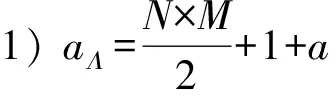
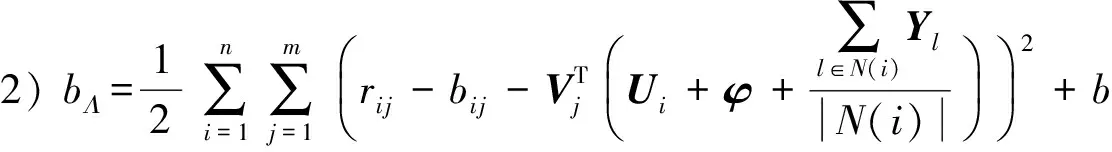
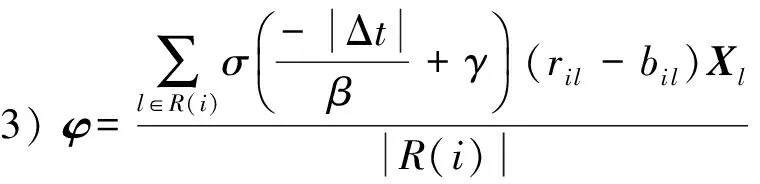
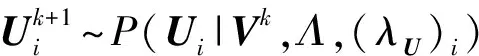
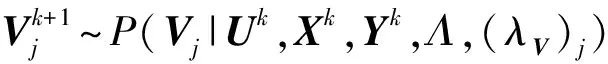
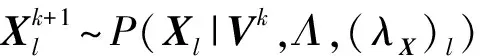
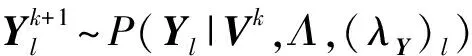
4 實驗和結果

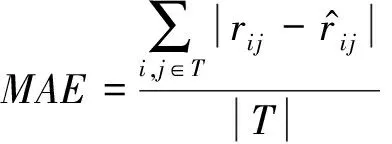
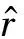
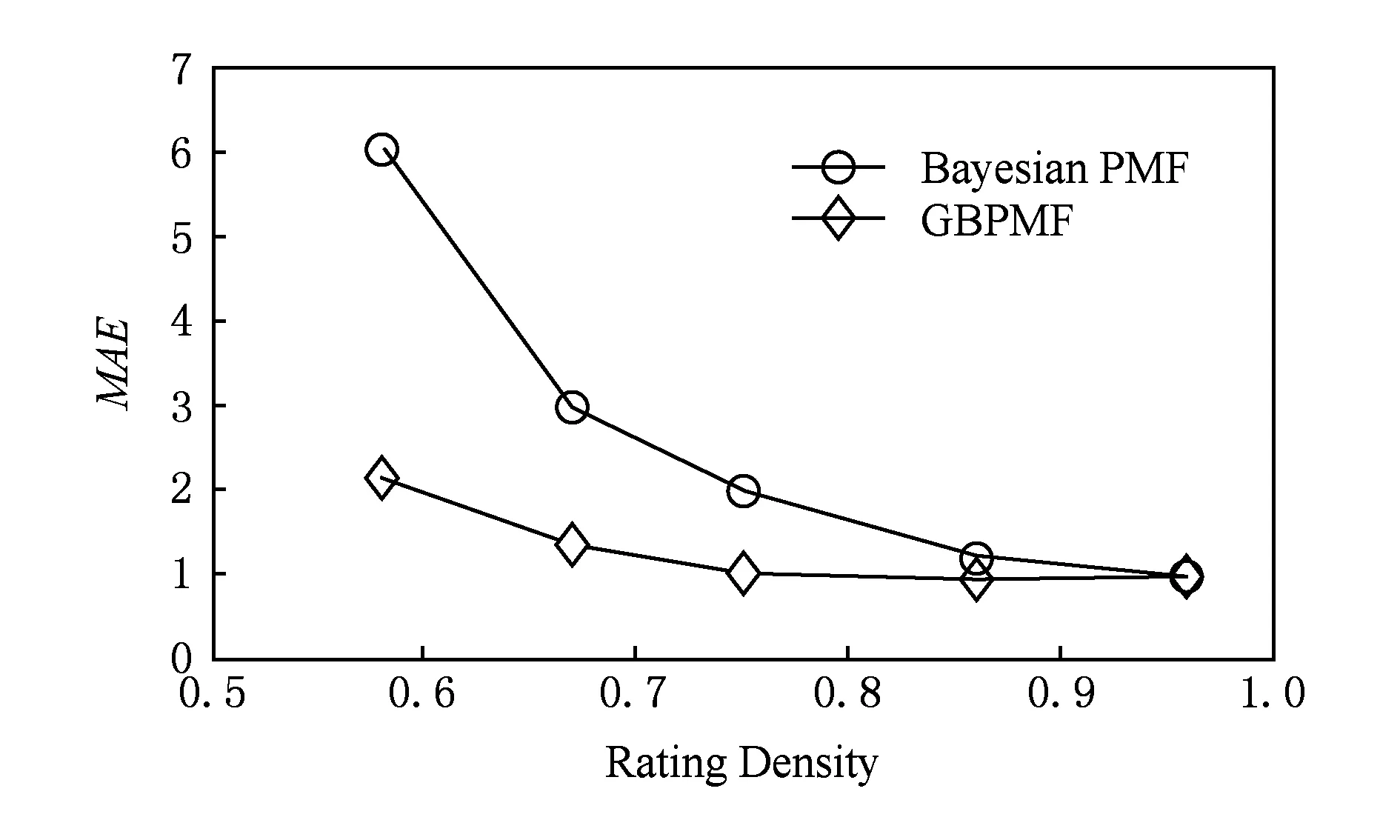
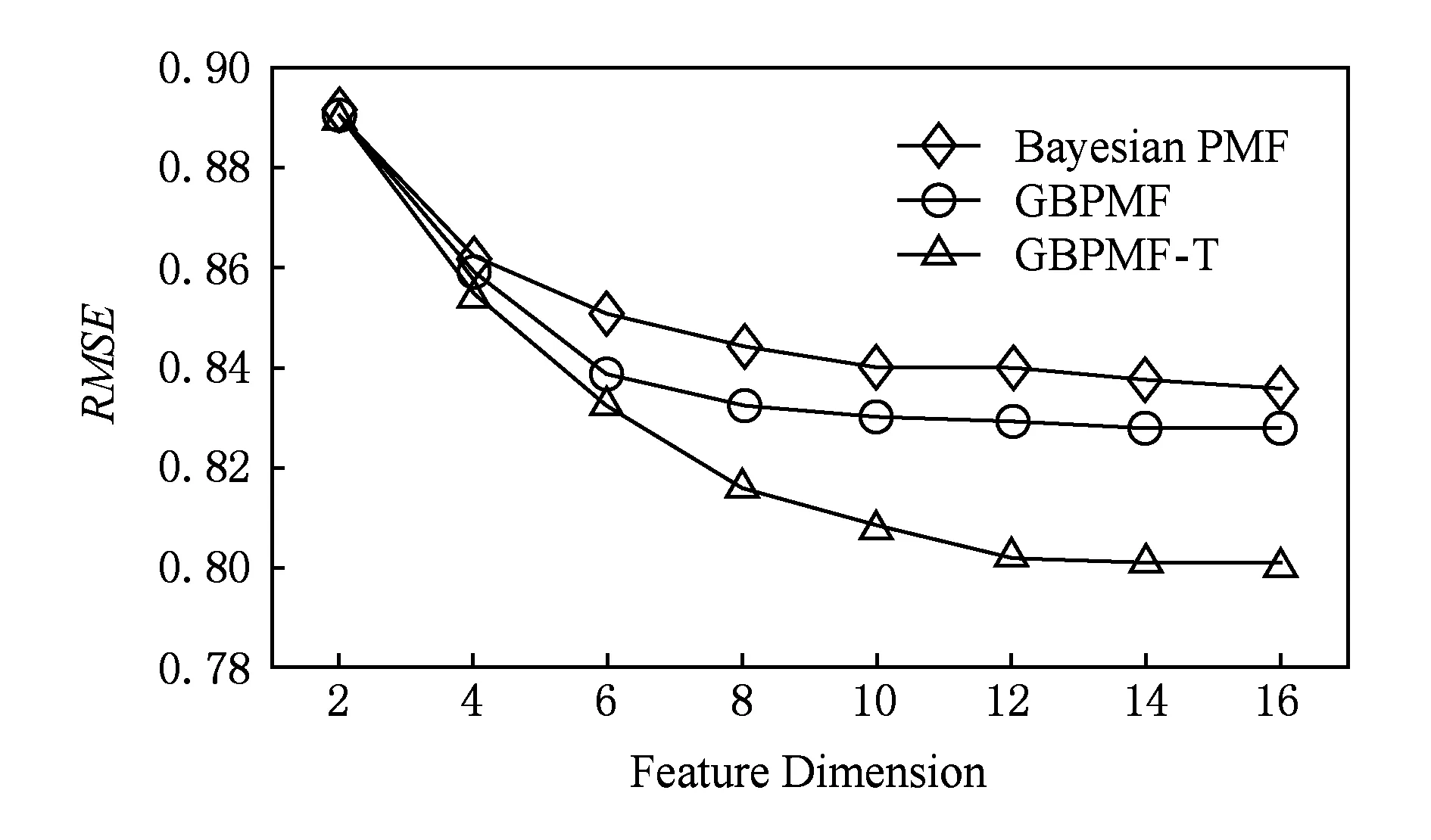
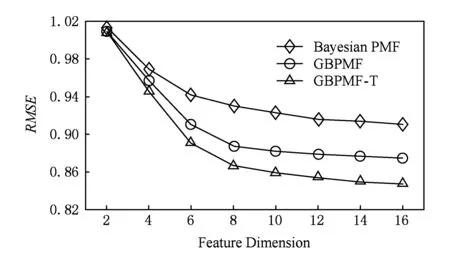
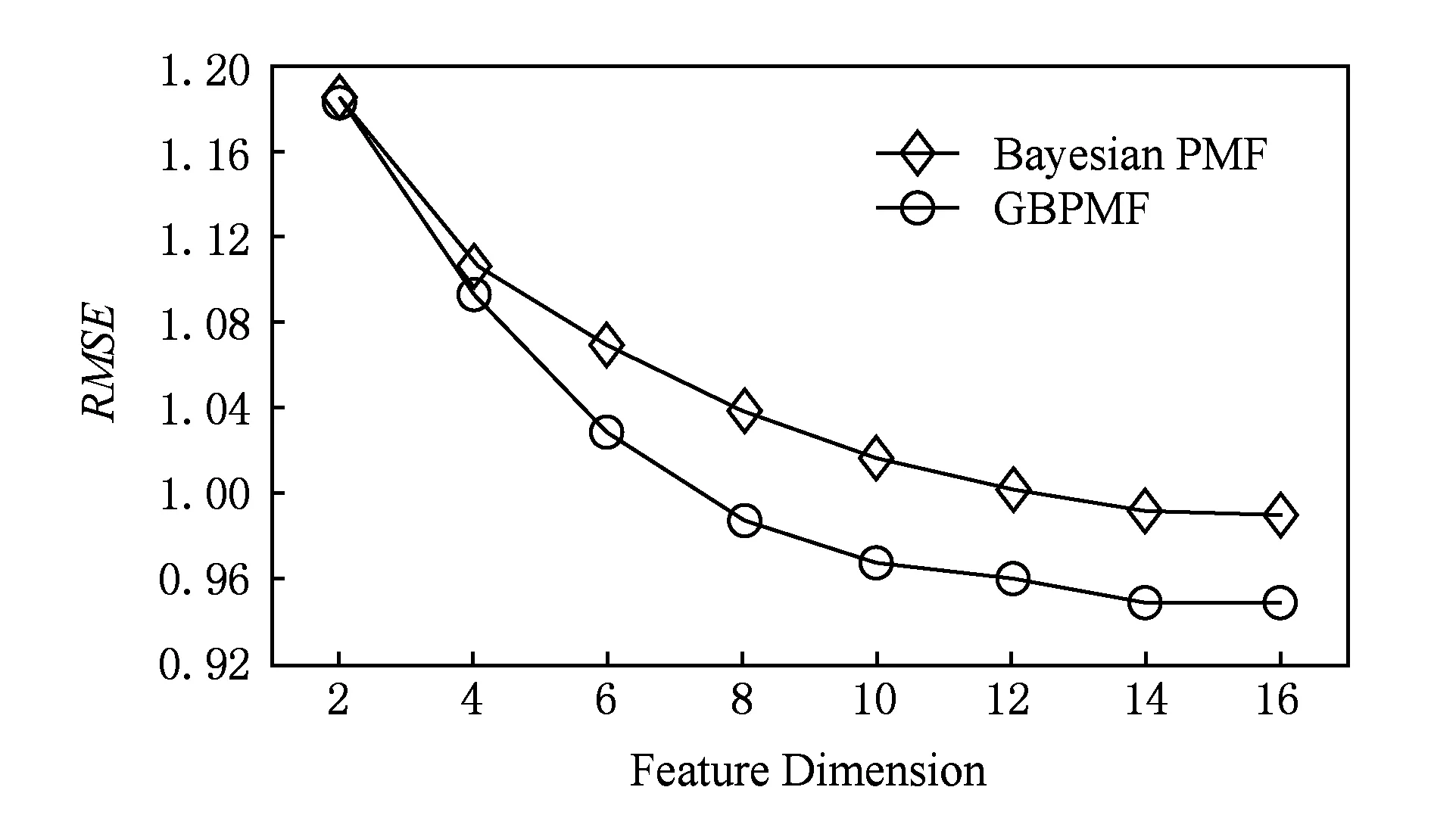
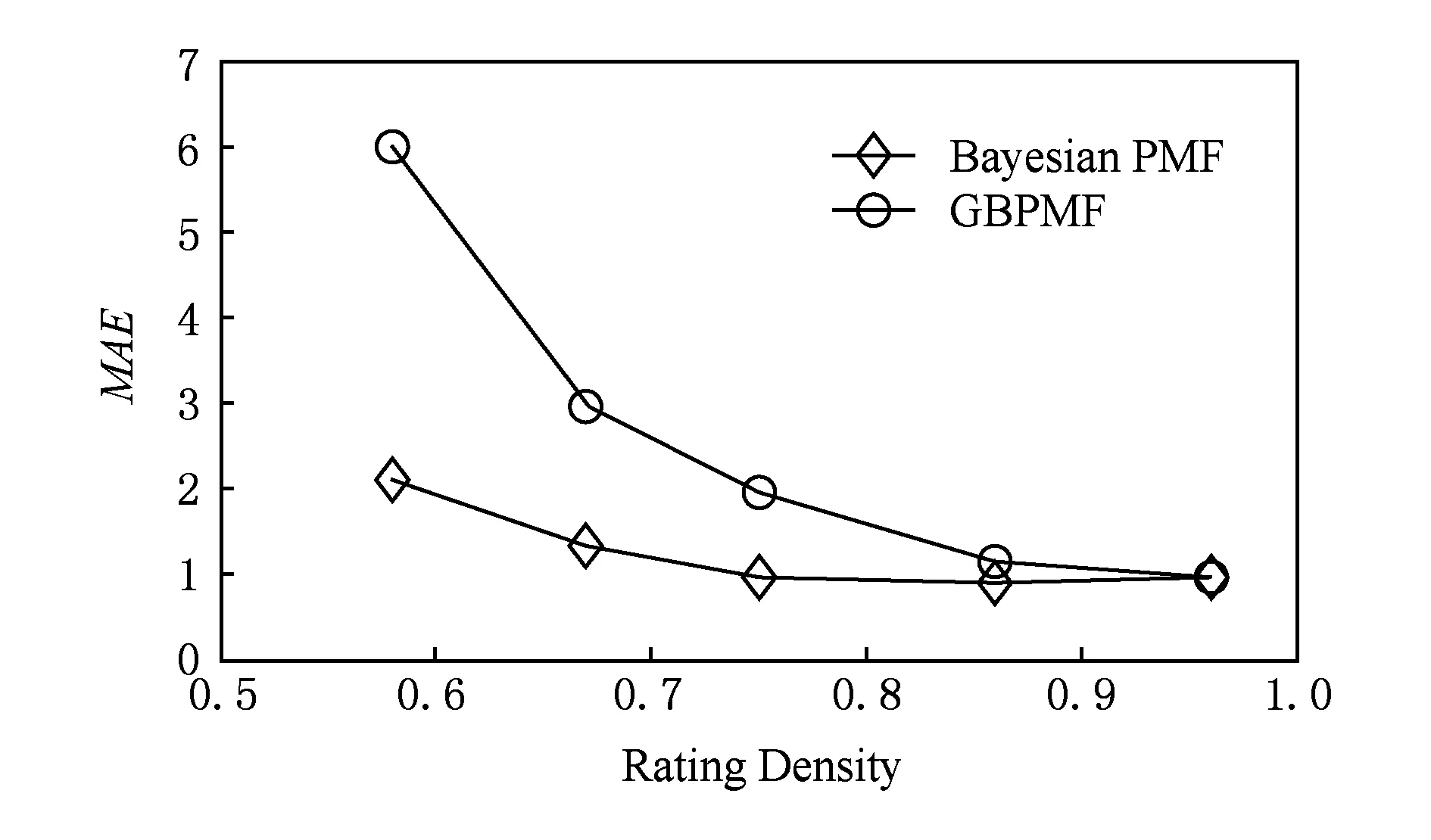
5 結束語





