水中人工心臟泵用磁軸承系統的模型及控制研究

孫 坤，陳 琛

（蘇州大學 機電工程學院，蘇州 215021）

水中人工心臟泵用磁軸承系統的模型及控制研究

孫 坤，陳 琛

（蘇州大學 機電工程學院，蘇州 215021）

提出水環境下磁懸浮血泵轉子運動模型，將水對泵轉子的作用等效成彈簧阻尼器，利用ADAMS與Simulink聯合仿真；并針對水中磁懸浮血泵，通過分析并調整PD控制器的微分系數，實現在保證轉子穩定性能的同時，改善轉子位移信號。

人工心臟泵；阻尼器；PD調節；改善信號

0　引言

磁軸承由于具有無機械摩擦、無接觸磨損、無需潤滑、定位精度高、轉速高且對環境無污染[1]等優點逐漸被人工心臟[2]、電主軸機床[1]等領域所應用。作為典型的開環非穩定系統，電磁軸承通過主動控制器，利用可控電磁力為懸浮轉子提供高精度的定位控制和振動阻尼控制[3]。

人工心臟用電磁軸承是在血液中工作的，但目前其建模以及控制器設計與一般工業用電磁軸承類似[4]，都是在空載環境下所進行的，再經過增益等方面的調節，使得血泵在液體中運行穩定。建模上的誤差無疑會導致磁懸浮系統運行性能較差，也阻礙了人工心臟用磁軸承的研制進程。另外對于磁懸浮血泵這類不規則的幾何模型，在水、血液等流體中的運動模型目前也很少有理論上研究。針對蘇州同心醫療公司的新一代磁懸浮人工心臟泵，如圖1所示，本文提出了水中磁懸浮系統模型，通過在ADAMS中建立機械模型，與Simulink聯合仿真。針對所使用的經典PD控制，考慮到水中磁軸承系統本身存在阻尼，對微分環節作適當減弱，以改善信號輸出。

圖1　同心醫療China Heart III磁懸浮人工心臟

1　磁懸浮系統理論建模

磁懸浮血泵同一般主動磁軸承原理相同，由徑向兩自由度（或四自由度）和軸向一自由度構成，因轉速不是太高且為剛性轉子，完全可以忽略陀螺效應，故其可以解耦為單自由度磁懸浮系統分別進行控制，這樣也方便了簡單PD控制器的應用。

對于水中磁懸浮系統，本文根據[1]關于單自由度磁懸浮系統模型，以及將水沖擊力視為平衡點附近位移和速度的函數[5]，寫出當泵轉子在靜平衡位置附近作小振動時，運動方程可以寫為：

其中，m為泵轉子質量，x為轉子徑向位移，kx為位移-力剛度系數，ki為電流-力剛度系數，kxx、kxv、kxv、cxx和cxy分別為轉子受水影響的剛度和阻尼系數。

從式(1)可以看到，一般磁懸浮只有負剛度，缺少阻尼項，所以是典型的開環非穩定系統，而PD控制的比例與微分環節實質上就是調整磁懸浮系統的剛度，并增加其阻尼成分[6]。而對于水中的磁懸浮泵，水對泵轉子恰好可以增加其阻尼項。

該型人工心臟用磁懸浮轉子為圓環狀，其頂端焊有葉片，水、血液等流體對該類型物體的作用較為復雜，很難從理論上進行推導研究，故本文將流體對泵轉子的作用等效為彈簧阻尼力。根據[7]及本磁懸浮系統結構參數，如表1所示，可以大致計算出c=30Ns/m，k=0.5N/m（忽略y方向對x方向耦合）。本文再對該泵環路測試，得到環路傳輸特性圖（如圖2所示）。從圖中可以看出，水載測試中，其阻尼增加值與計算值偏差不大，說明水中泵轉子運動模型較為合理。初取c=24Ns/m，k=0.5N/m，以便在ADAMS與Simulink仿真中作微調。

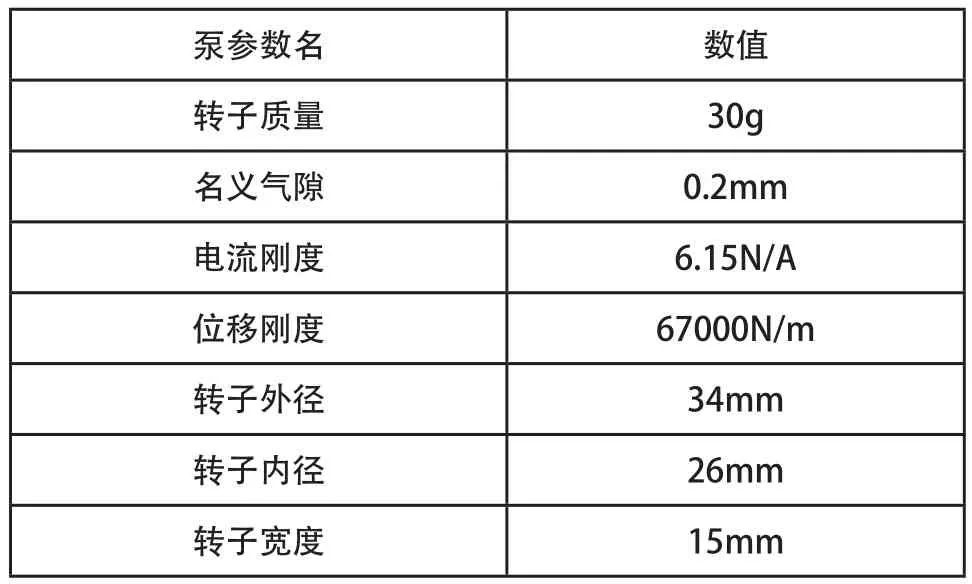
表1　系統結構系數

圖2　人工心臟泵環路傳輸特性

2　ADAMS與Simulink聯合仿真

磁軸承系統研究一般把其力學系統看作傳遞函數，通過MATLAB/Simulink對磁懸浮軸承整體系統進行仿真的，但是這種仿真在建立系統機械模型時，尤其是在液體環境下，不夠精確，而ADAMS能夠更好地綜合考慮各個因素對磁懸浮軸承整個系統的影響，對現實的實驗也具有更好的指導意義[8]。

首先在SolidWorks建立磁懸浮泵的幾何模型，把它導入ADAMS里面。在ADAMS中定義定子固定約束，轉子為平面副，并設置與定子碰撞接觸。為了考慮水對泵轉子的作用，在泵轉子與定子之間建立徑向均布5個彈簧拉壓阻尼器，其阻尼即為上文所計算值。設置狀態變量有x、y方向徑向力x、y方向位移，并將x、y方向徑向力設為輸入變量，x、y方向位移設為輸出變量。

控制系統是用MATLAB/Simulink模塊來設計，由上述可知，磁懸浮泵式不穩定的，因此采用PD控制對系統仿真，環路還包含一個相位超前環節以及傳感器低通、功率放大器環節，如圖3所示。圖4(a)是未考慮阻尼時的階躍響應，圖4(b)是考慮了阻尼的響應，可以發現考慮阻尼時的響應時間稍慢些，但超調量很小。說明水抑制了泵轉子的振蕩，改善了泵轉子的性能。并通過對該泵進行空載與水載起浮試驗（如圖5所示，a.空載，b.水載），可以看出水載時的起浮較為平穩，大約需要5ms，而空載時稍快一些。通過微調ADAMS模型中的阻尼值至c=20Ns/m，響應時間相當吻合。

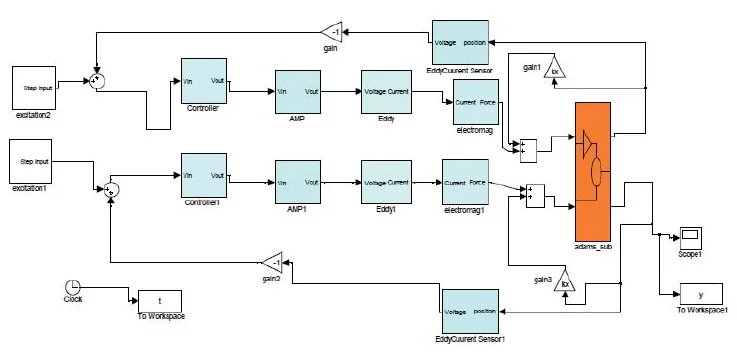
圖3　磁懸浮系統ADAMS/Simulink聯合仿真模塊圖

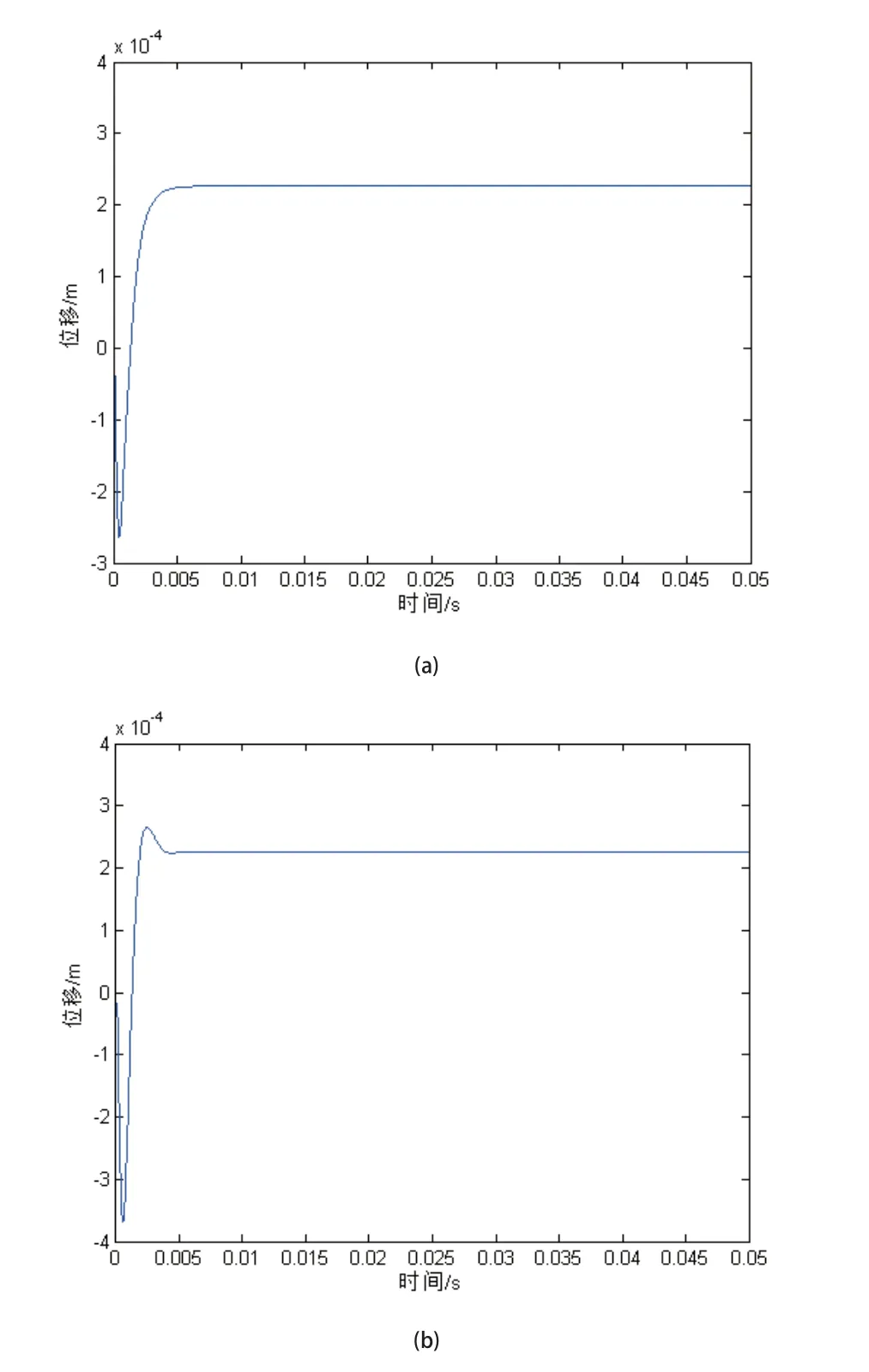
圖4　磁懸浮系統階躍響應模塊

圖5　磁懸浮泵空載與水載起浮試驗

3　PID微分環節的調節

從圖6(a)可以看出，空載時的轉子起浮是穩定的，滿足性能要求，只是在起浮后期有170ms的振蕩，而水載時圖6(b)幾乎沒有振蕩。因此，我們可以針對該人工心臟泵，考慮放寬微分環節，以此減弱微分對高頻噪聲放大的影響。本文共設置了遞減的4個微分系數Td=0.0013288、0.0011、0.00077和0.00044（通過改變電阻值），分別探究泵轉子起浮性能及位移信號的改善程度。

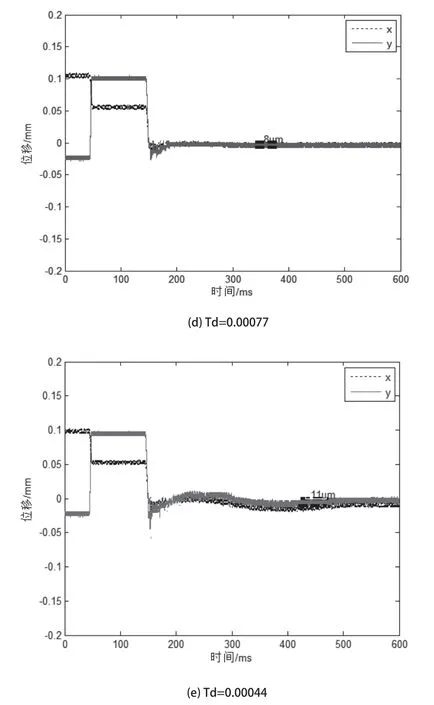
圖6　各不同條件下泵轉子全起浮過程位移輸出（a.空載, b-e.水載）

從圖中可以看出，在Td降至0.0011時，起浮很好，并未出現振蕩，位移信號有所改善。當降至0.00077時，起浮仍然穩定，稍有振蕩，但位移信號含噪量明顯降低。再降至0.00044時，有明顯振蕩，振幅達到50um，位移信號未出現改善，此時表明系統已出現阻尼不足，趨向不穩定，更起不到對輸出信號的改善作用。因此表明，針對水中磁懸浮運行的控制系統可以空載控制系統為基礎，且充分利用水中模型的特點，適當調節微分環節，達到實現穩定性能良好的同時改善輸出信號質量。

4　結論

本文針對人工心臟泵用磁懸浮系統，建立了水中磁懸浮系統模型，引入阻尼項，并借助ADAMS與Simulink聯合仿真，表明了水對磁懸浮泵轉子振蕩的抑制作用。又通過調節空載下PD控制器的微分項，減弱對微分的需要，探索水的作用對于磁懸浮系統阻尼的放寬程度，從而在保證泵轉子性能穩定且良好的同時降低位移噪聲。

【】【】

[1] Gerhard Schweitzer, Eric H. Maslen.Magnetic Bearings-Theory, Design,and Application to Rotating Machinery[M]. New York： Springer,2009.

[2] Nojir, C.,Kiijima,T.,Maekawa,J..Recent Progress in the Development of Termo Implantable Left Ventricular Assist System[J].ASAIO Journal,1999,45(3)：199-203.

[3] 謝振宇,張景亭,高華,等.帶阻尼器磁懸浮軸承轉子系統的不平衡響應[J].中國機械工程,2009,20(3)：327-330.

[4] 雷世東,袁小陽.人工心臟電磁軸承概念設計的知識基礎[J].機械科學與技術,2004,23(3)：293-296.

[5] 聞邦椿,顧家柳,夏松波,等.高等轉子動力學[M].北京：機械工業出版社,2000.

[6] A. Chiba,T.Fukao,O.Ichikawa. Magnetic Bearings and Bearingless Drives[M].Oxford：Elsevier,2005.

[7] 董躍.液壓軸承油膜穩定性分析[J].機電產品開發與創新,2012,25(5)：155-157.

[8] 馮恒.磁懸浮軸承系統仿真研究[D].南京航空航天大學,2010.

Research on model and control of magnetic bearing applied in artifi cial heart in the water

SUN Kun, CHEN Chen

TH133.3

A

1009-0134(2016)07-0005-04

2016-03-19

孫坤（1992 -），男，江蘇漣水人，碩士研究生，研究方向為人工心臟、磁懸浮軸承控制以及有限元仿真等。