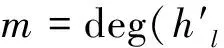環Fp+uFp+…+uk-1Fp上(1-u)-常循環碼的深度譜

鄭喜英,孔 波

(1.黃河科技學院信息工程學院,中國 鄭州 450063; 2. 河南財政金融學院數學與統計學院，中國 鄭州 450046)

?

環Fp+uFp+…+uk-1Fp上(1-u)-常循環碼的深度譜

鄭喜英1*,孔 波2

(1.黃河科技學院信息工程學院,中國 鄭州 450063; 2. 河南財政金融學院數學與統計學院，中國 鄭州 450046)

本文研究環Fp+uFp+…+uk-1Fp上長為n(這里p?n)的(1-u)-常循環碼的生成多項式. 基于差分運算的線性性質及環Fp+uFp+…+uk-1Fp上(1-u)-循環碼的結構,給出其上(1-u)-常循環碼的深度譜.

有限鏈環；常循環碼；深度譜；深度分布

有限環上常循環碼理論的研究是目前的熱點問題. Etizion[1]把微分運算應用到線性碼中,給出了一些碼的深度分布. Mitchell[2]用整數值有理多項式的理論給出了二元循環碼的深度分布.Luo等[3]利用矩陣理論給出了線性碼深度分布的一般計算公式, 給出了有限域上線性碼的深度分布和深度譜. 廖群英等[4]給出了兩類環上線形碼的深度譜和深度分布的計算公式. 石立葉等[5]在研究了四元循環碼生成多項式的基礎上給出了四元循環碼的深度譜. 鄭喜英等[6]給出了環Zpm上循環碼的深度譜. Chen等[7]給出了環Fpm+uFpm上長為2ps常循環碼的結構. 石立葉等[8]用差分運算的線性性質給出了有限域上循環碼的深度分布. 施敏加等[9]研究了環Fq+uFq+…us-1Fq上常循環碼的結構. Kai等[10]研究了有限環F2+uF2+vF2+uvF2上長為奇數的Fp+uFp+…uk-1Fp-常循環碼的結構. Chen等[11]研究了有限域上的常循環碼的等價性, 并對其上常循環碼的生成員進行了刻畫. 向躍明等[12]給出了半本元環的一些刻畫. 鄭喜英等[13]給出了有限鏈環上循環碼的深度分布. 本文的第一部分對環p上常循環碼和深度分布及深度譜的概念和性質進行了介紹. 第二部分根據環p上(1-u)-常循環碼的結構給出了該環上的(1-u)-常循環碼深度譜.

文中出現的p均是素數,(n,p)=1,環Fp+uFp+…+uk-1Fp均記為R.

1 基本概念

定義1 環R上長為n的線性碼是R-模Rn的一個加法子模. C為環R上長度為n的線性碼,如果?c=(c0,c1,…,cn-1)∈C ?((1-u)cn-1,c0,c1,…,cn-2)∈C, 則稱C為(1-u)-常循環碼.

本文中的(1-u)-常循環碼均認為是線性的.

C是環R上長為n的循環碼的充分必要條件是C是R[x]/(xn-1)的理想. C是環R上長為n的(1-u)-常循環碼的充分必要條件是C是R[x]/(xn-1+u)的理想.

下面定義3個線性算子.

(1) ?x=(x1,x2,…,xn)∈Rn定義x的差分為D(x)=(x2-x1,x3-x2,…xn-xn-1).約定n=1時D(x)=0. 當1

(2) 對任意多項式l(x)∈R[x],定義線性算子

Ll(x):R[x]/(xn-1+u)→R[x]/(xn-1+u),

證明同文獻[5]引理2.1.

定義2 對向量x=(x0,x1,…,xn-1)∈Rn, 稱使Di(x)=0成立的最小非負整數i稱為向量x的深度, 記為depth(x), 否則記x的深度為n.

定義3[3]設C是環R上長為n的線性碼, Di表示碼C中深度為i的碼字的個數, 則集合{D0,D1,…,Dn}稱為碼C的深度分布, {i|Di≠0,1≤i≤n}為碼C的深度譜,記作Dept(C). 約定Dept({0})=?.

引理3 (1) D是從Rn到Rn-1的滿線性同態；

(2) 若depth(x)=d>t>0, 則depth(Dt(x))=d-t；

(3) Dept(Rn)={1,2,…,n}.

證 將文獻[8]中引理2.5證明中的F換成R即可.

引理4 設C是環R上長為n的碼, 記C′=Di(C)是碼C通過算子Di在Rn-i中的像, 這里1≤i≤n, 記C″={c∈C| Di(C)=0},則

Dept(C)=Dept(C″)∪(i+Dept(C′))

證 將文獻[5]中定理2.6證明中的F換成R即可.

2 主要結果

證 由

(1)

可知C是R[x]/(xn-1+u)的理想且在算子Lx-1之下封閉, 得線性同態

(2)

記f′(x)=(x-1)ef1(x),則(2)的像是由f′(x)生成的(1-u)-常循環碼, 記為C′, 檢驗多項式是h1(x),所以C′={g(x)f′(x)mod(xn-1+u)|g(x)∈R[x]}. 因C′的生成多項式是首一的且次數為n-t且dimC′=degh1(x)=t. 則可以將線性映射(2)改為線性滿同態

(3)

由于s+t≤n, 即n-s-t≥0,且C′是(1-u)-常循環碼.

進一步考慮線性變換

(4)

(5)

進一步,對C′考慮截取算子,可得下面的線性同構

(6)

Dn-t:C→Rt

C″={c∈C| Dn-t(c)=0}=

(7)

Dept(C)=Dept(Ker(Dn-t))∪(n-t+Dept(lmf(Dn-t)).

Dept(C)=Dept(C″)∪(n-t+Dept(Rt))={1,2,…,s}∪{n-t+1,n-t+2,…,n}={1,2,…,s,n-t+1,n-t+2,…,n}.

根據定理1,2可得下面的定理：

{1,2,…,s1,n-(m1-s1)+1,n-(m1-s1)+2,…,n;…;

1,2,…,sk,n-(mk-sk)+1,n-(mk-sk)+2,…,n}

綜上可得,環R長為n的(1-u)-常循環碼的深度譜為集合

{1,2,…,s1,n-(m1-s1)+1,n-(m1-s1)+2,…,n;…;

1,2,…,sk,n-(mk-sk)+1,n-(mk-sk)+2,…,n}.

[1] ETIZION T. The depth distribution: a new characterization for linear codes [J]. IEEE Trans Infor Tech, 1997,43(4):1361-1363.

[2] MITCHELL C J. On integer-valued rational polynomials and depth distributions of binary codes [J]. IEEE Trans Infor Tech, 1998,44(7):1346-1350.

[3] LUO Y, FU F W, WEI V. On the depth distribution of linear codes [J]. IEEE Trans Inform Theor, 2000,46(2):2197-2203.

[4] 廖群英,蒲可莉. 環上線性循環碼的深度譜以及深度分布的一個注記[J]. 四川師范大學學報(自然科學版), 2013,36(2):159-164.

[5] 石立葉,樊 惲. 四元循環碼的深度分布[J]. 華中師范大學學報(自然科學版), 2009,43(3):355-358.

[6] ZHENG X Y, KONG B. The depth spectrums of linear cyclic codes on ring zpm[C]// IEEE Youth Conference on Information, Computing and Telecommunication, Beijing, 2010:162-165.

[7] CHEN B C, HAI Q D, LIU H W,etal. Constacyclic codes of length 2psoverFpm+uFpm[J]. Finite Fields Their Appl, 2016,37(5):108-130.

[8] 石立葉,循環碼的深度分布[D].武漢：華中師范大學, 2007.

[9] 施敏加,朱士信. 環Fq+uFq+…us-1Fq上的常循環碼[J]. 中國科學技術大學學報， 2009,39(6):583-587.

[10] KAI X S, ZHU S X, WANG L Q. A family of constacyclic codes overF2+uF2+vF2+uvF2[J]. J Syst Sci Compl, 2012,25(5):1032-1040.

[11] CHEN B C, FAN Y, LIN L R,etal. Constacyclic codes over finite fields[J]. Finite Fields Their Appl, 2012,18(6):1217-1231.

[12] 向躍明, 吳毅清. Small理想都是投射的環[J]. 湖南師范大學自然科學學報, 2012,35(1):1-4.

[13] 鄭喜英, 常曉鵬. 有限鏈環上循環碼的深度分布[J]. 河南大學學報(自然科學版), 2012,42(4):347-350.

(編輯 HWJ)

The Depth Spectrum for (1-u)-Constacyclic Codes overFp+uFp+…uk-1Fp

ZHENGXi-ying1*,KONGBo2

(1. Institute of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450063, China；2. School of Mathematics and Statistics, Henan Institute of Economy, Zhengzhou 450046, China)

The generator polynomial for (1-u)-constacyclic codes of lengthnover the ringFp+uFp+…+uk-1Fpis established whenp?n. In light of the linear property of difference and the structure of (1-u)-constacyclic codes over ringFp+uFp+…+uk-1Fp, the depth spectrum of (1-u)-constacyclic codes over the ring is given.

finite chain ring; constacyclic code; depth spectrum; depth distribution

10.7612/j.issn.1000-2537.2016.06.015

2015-10-17

河南省基礎與前沿項目(162300410083)；鄭州市科技局項目(20141375)

O157.4

A

1000-2537(2016)06-0085-04

*通訊作者,E-mail：zxyccnu@163.com