數學期望考題的新動向

■陜西省神木縣職業技術教育中心

高 平

?

數學期望考題的新動向

■陜西省神木縣職業技術教育中心

高 平

近年來高考考查離散型隨機變量的數學期望的試題，具有內容新、背景新、結構新、實際應用性強等特點。下面結合實例談談近年高考考查數學期望的新動向，供同學們參考。

一、取材新

不難發現數學期望的試題也融入新課標的教育理念，多角度、多視點地考查同學們的數學素養。關注學生生活，注重社會現實，體現時代精神，體現社會熱點，關注當前科技新發展，試題中有大量的生活背景，充分體現了“從生活走向數學，從數學走向生活”的理念。

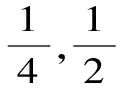
(1)求出甲、乙所付租車費用相同的概率；

(2)求甲、乙兩人所付的租車費用之和為隨機變量ξ，求ξ的分布列與數學期望Eξ。

則所付費用相同的概率為：

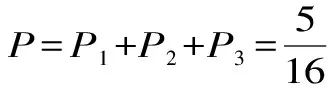
(2)設甲，乙兩人所付的費用之和為ξ，ξ可為0,2,4,6,8。

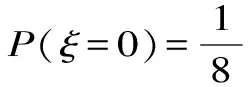
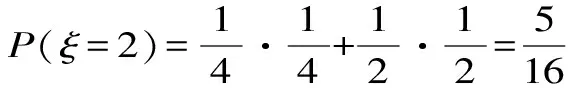
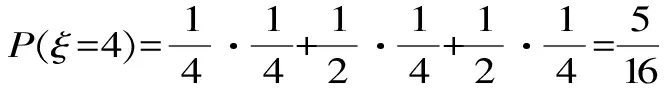
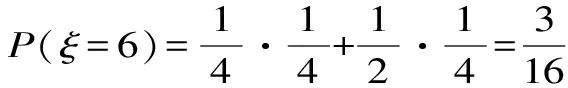
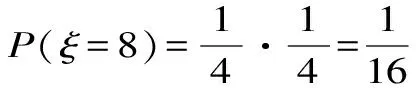
分布列為：

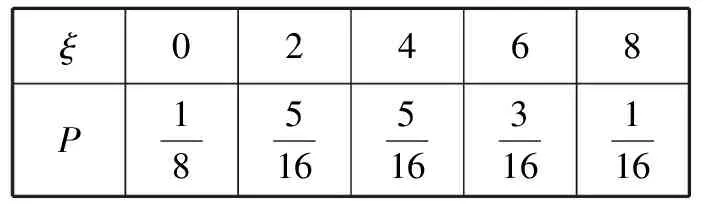
ξ02468P18516516316116

二、情境新

例2 馬老師從課本上抄錄一個隨機變量ξ的概率分布列如下：

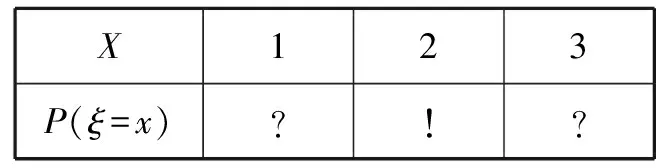
X123P(ξ=x)？?。?/p>

請小牛同學計算ξ的數學期望。盡管“！”處完全無法看清，且兩個“？”處字跡模糊，但能斷定這兩個“？”處的數值相同。據此，小牛給出了正確答案Eξ=____。

解析：初看此題，與平時給出的分布列很是不同，第二行的概率值都沒有給出，為同學們的答題設置了障礙。但嘗試從基本思路出發解決本題，卻發現非常簡單：變量ξ的期望Eξ=1×?+2×!+3×?=4×?+2×!=2(!+2×?) ，而“!+2×?”剛好就是事件概率的性質——概率和為1，這樣就能很快得出結果2。

例3 (2015年福建理科卷)某銀行規定，一張銀行卡若在一天內出現3次密碼嘗試錯誤，該銀行卡將被鎖定。小王到銀行取錢時，發現自己忘記了銀行卡的密碼，但是可以確定該銀行卡的正確密碼是他常用的6個密碼之一，小王決定從中不重復地隨機選擇1個進行嘗試。若密碼正確，則結束嘗試；否則繼續嘗試，直至該銀行卡被鎖定。

(1)求當天小王的該銀行卡被鎖定的概率；

(2)設當天小王用該銀行卡嘗試密碼次數為X，求X的分布列和數學期望。

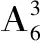
依題意得，X所有可能的取值是1，2，3。

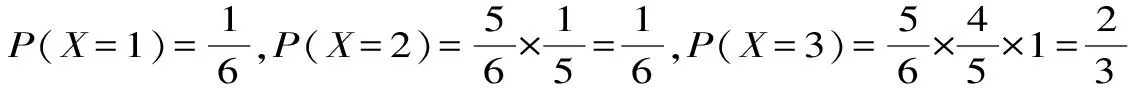
所以，X的分布列為：

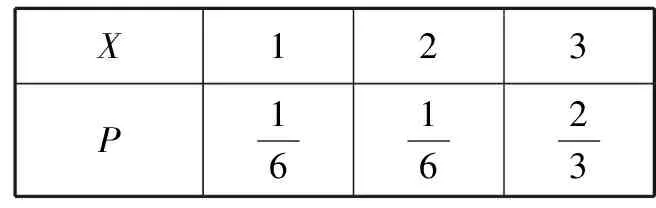
X123P161623

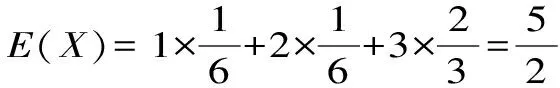
三、注重知識的交匯

在知識網絡交匯點設計試題是高考數學命題的新特點和大方向，高考中的數學期望試題也不失時機地體現了這一動向。

例4 設S是不等式x2-x-6≤0的解集，整數m,n∈S。

(1)記使得“m+n=0成立的有序數組”為事件A，試列舉A包含的基本事件;

(2)設ξ=m2，求ξ的分布列及數學期望Eξ。

解析：(1)由x2-x-6≤0得，-2≤x≤3，即S={x|-2≤x≤3}。由于整數m,n∈S且m+n=0，所以A包含的基本事件為(-2，2)，(2，-2)，(-1，1)，(1，-1)，(0,0)。

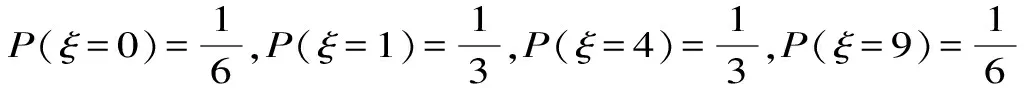
故ξ的分布列為：

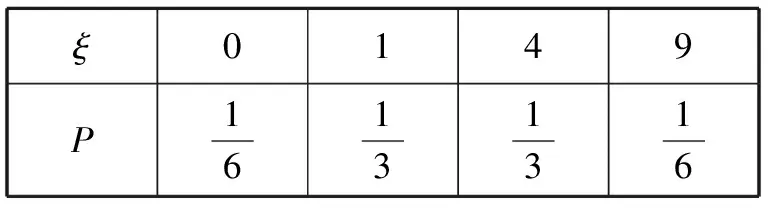
ξ0149P16131316

(責任編輯 徐利杰)