高中概率統計與風險投資決策
竇一鳴
摘要:高中數學知識與經濟學的相關理論具有密切的聯系,本文從高中概率與統計知識出發,簡單介紹了其在經濟領域風險投資決策方面的具體應用,以此來說明,在高中數學理論教學過程中,適當引入經濟學案例,對教學的輔助作用,以及對學生日后大學學習的重要幫助。
關鍵詞:概率 統計 期望 方差 投資決策
一、高中數學引入財務管理及金融等經濟理論的必要性
數學作為一門重要的自然學科,為人文社科的研究提供了必要的分析工具和方法,高中數學中涉及的概率論及數理統計知識,為學生進入大學的數學學習打下了基礎,大學中企業管理、財務會計、金融學、經濟學等學科都需要借用數學模型和公式予以定量分析。所以在高中學習階段很有必要將一些的簡單經濟理論引入到數學課堂教學中,一則豐富課堂教學的案例資源,將抽象的數學知識轉化為生動的經濟問題;二則可以為學生進入大學學習做必要的鋪墊。
二、高中概率論與數理統計知識點概述
我們日常的經濟生活中涉及到計算的問題大都屬于概率與統計的問題。概率統計的條件與結果之間的聯系有時并沒有必然性,也就是說在同一情況下,完全有可能會發生不同的結果。
(一)概率與統計
等可能性事件是我們日常生活中接觸最多的概率問題, 簡單的來說就是某件事包含基本事件a個,基本事件的總數為b個,則這一事件A發生的概率為:
P(A)= card(A)/ card(I)
=a/b
(二)期望和方差
期望和方差是常用隨機變量的兩個重要特征,它們是對隨機變量的一種理性的數理分析,是我們用來分析預估風險和收益的重要參考標準。
1、期望
假如 X 為離散型隨機變量,則它的概率分布為 P(X=XK)=Pk (k=1,2,3…),稱為和數,記為
X1P2+X2P2+…+XkPk+…=∑XkPk
它是隨機變量 X 的數學期望,稱之為期望,記作
E (X)= ∑XkPk
若 X 為連續型隨機變量,它的概率密度為 f(x),則 X的數學期望為
期望體現了隨機變量取值范圍意義上的一種“平均”,所以在對不確定性因素的分析中,利用期望值分析發揮了其極重要的作用。
2、方差
方差的分析是建立在是在期望的基礎上的,是(f x)=[X- E (X)]2的數學期望,所以離散型隨機變量及連續型隨機變量的方差可以統一記為
D (X)=E [X- E (X)]2
方差D (X)表示X的取值將偏離其期望值E(X)的程度大小,在具體經濟學的應用中,對分析風險和預估收益都有著重要的作用。方差的簡化公式為
D (X)=E (X2)- [E (X)]2
三、概率論與數理統計在企業風險投資決策中的具體應用
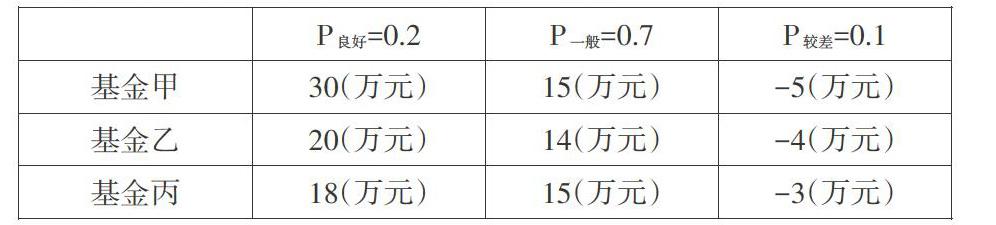
以投資基金項目為例,若企業或個人將一筆資金投入到三個不同的項目甲、乙、丙中,不同的基金項目在不同的經濟環境下收入不同,假設對應的外部經濟環境可以大致分為良好、一般、較差三個級別,根據每個基金不同的數據參數可以得到不同的經濟環境下甲、乙、丙三個基金的收益及發生概率,其分布情況如表所示:
通過分析以上離散型隨機變量的期望和方差之后我們可知,基金甲的投資平均收益最大。但基金甲的投資風險也最大,基金乙的風險次之,同時基金乙的收益也是三者中最小的。基金丙的收益比基金甲低13.75%,但是其風險比項目甲低62.78%,基金乙的收益比甲低16.25%,但是其風險比甲低54.27%,這符合投資領域高風險、高收益的規律,所以綜合比較,基金丙的收益在三個項目中排第二,但是其風險在三個項目中最小,所以作為一個理性的投資人,應該綜合比較投資收益與投資風險的匹配度,所以最佳的理性決策應該選擇投資基金丙。
四、結束語
通過以上的分析可以看出,高中數學的概率論及數理統計知識在風險投資決策中發揮了重要作用。其實在整個經濟學的發展過程中,數學作為一門定量分析工具無處不在,如企業的成本性態分析運用的是高中數學的線性函數知識;杠桿效應的分析運用的是高中微積分的知識等等。所以在高中數學的教學階段,適當地引入經濟學的相關理論,可以更好地幫助學生理解數學知識,不僅可以提高學習的興趣及效率,同時為學生進入大學及走入社會進行投資理財,打下良好的數學基礎。
參考文獻:
[1]財政部會計資格評價中心.財務管理[M].北京:中國財政經濟出版社,2015
[2]胡玉明.財務報表分析[M].大連:東北財經大學出版社,2012
[3]童嘉森.樂學易考高中教材數學(高三)[M].北京:人民教育出版社 ,2006
[4]李昱筱.概率統計與經濟學初識[J].科技風,2016,2

