180°方形截面彎管內流動特性研究*

周 佳 朱目成 巫帥珍 羅月迎 賈傳偉

(西南科技大學 制造過程測試技術教育部重點實驗室)

180°方形截面彎管內流動特性研究*

周 佳*朱目成 巫帥珍 羅月迎 賈傳偉

(西南科技大學 制造過程測試技術教育部重點實驗室)

針對180°方形截面彎管內復雜的流動特性以及出現二次流現象等問題，運用Fluent軟件對連續方程和納維-斯托克斯方程進行空間離散，對180°方形截面彎管內的流動進行數值模擬計算。模擬計算結果與實驗測量的結果基本相一致，說明建立的數學模型與數值方法是有效的。同時，分析了彎管內二次流形成與發展的現象，得出了二次流的變化規律。這為揭示180°方形彎管內復雜流動現象的作用機理提供了參考，對于機械設備的制造和應用具有一定的意義。

180°方形彎管 Fluent N-S方程 湍流 數值模擬 二次流

隨著我國流體機械制造業的持續發展，彎管被廣泛應用于如石油化工流體的輸送、發電廠、水利、船舶和核電站冷卻水循環系統等場合。彎管作為機械設備中的重要部件之一，在機械設備的設計、制造、使用和維護過程中都需要考慮彎管的流場特性對機械設備的影響。因此，研究彎曲管道內的流動特性具有一定的理論和工程實用價值。自20世紀20年代圓形截面彎管內二次渦流現象第一次被Dean W R提出后[1]，彎管內的二次流問題吸引了許多學者的研究[2，3]。Sudo K等采用旋轉探針技術對90°圓形截面管道內的紊流流場經行研究，得出了雷諾應力等值線圖、矢量圖和軸向截面的速度等值線圖[3]。Taylor A M K P使用LDV對90°彎曲管道內形成的湍流和層流進行了測量，得到了時均速度、脈動速度和壁面壓力分布等實驗數據[4]。江山等對90°圓形截面彎管內湍流流場經行了數值模擬，分析了二次流形成的原因，給出了二次流影響彎管內壁壓力和速度分布的規律[5]。曾實和Manners A采用大渦模擬模擬了180°方形截面彎管的湍流流動[6]。徐俊等使用激光多譜勒測速儀完成了對180°彎管流場信息的實驗測定[7]。

以往研究主要針對90°彎管內部流場進行測量和模擬，以及對180°彎管內部流場的測量，缺乏對180°方形截面彎管內湍流流場的研究分析，特別是二次流的詳細分析。當前，隨著現代科技的發展，數值模擬計算以其代價小、收效快的特點在科研方面占據的地位越來越重要，各種流體力學軟件已被廣泛應用在數值模擬計算領域[8]。筆者為研究180°方形截面彎管內的流動特性，使用Fluent流體計算軟件，采用RNGk-ε湍流模型，對彎管內的湍流流動進行了模擬，得出詳細的流場特性，重點考察流場速度和壓力分布的變化規律以及彎管內橫截面上產生二次流動現象。

1 物理模型

本文研究的物理模型為180°方形截面彎曲管道，其幾何尺寸如圖1所示。彎管的半徑比為Rc/D=2.5，Rc=0.5(r1+r2)，方形截面邊長D為100mm，左右兩側的直線段長度為500m，θ為極角，彎管開始彎曲截面為θ=0°，結束彎曲截面為θ=180°，彎曲內側半徑r1=200mm，外側半徑r2=300mm。

2 數學模型

2.1控制方程

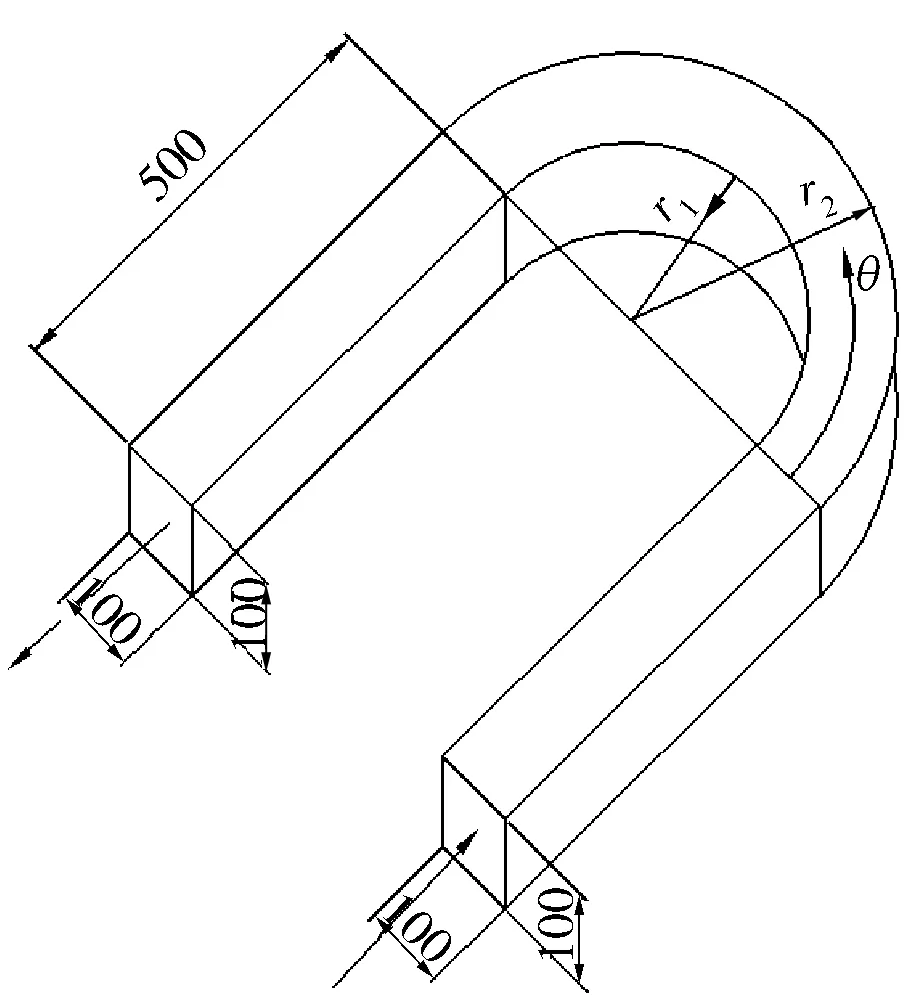
圖1 180°方形截面彎管截面尺寸

通過對連續方程和瞬時納維-斯托克斯方程進行時均化處理，得出在直角坐標系下的定常、絕熱、不可壓縮流體滿足的控制方程：

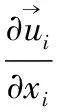
(1)

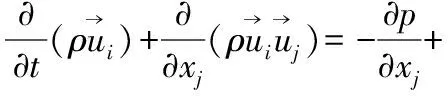
(2)

式中p——平均壓強；

Si——源項；

2.2RNGk-ε湍流模型

20世紀80年代，Yakhot V和Orszag S A在分析了以往研究者的成果以后，首次系統地運用RNG方法研究了湍流流場，提出在慣性子區域中湍流可用隨機力作用下的納維-斯托克斯方程描述[9]。該RNGk-ε模型既適用于高Re情況，也適用于低Re湍流的流動，提出了使用有效粘性系數的微分表達式，來描述低雷諾數情況的流動過程：

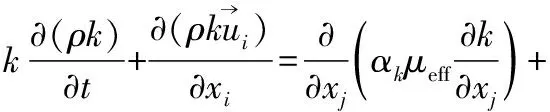
Gk-ρε

(3)

(4)

其中，αk、αε分別代表k、ε的反向有效Prandtl數，Gk代表由平均速度梯度引起的湍動能生成項。

S=(2SijSij)1/2

αk=αε=1.39,Cμ=0.085,C1ε=1.42,C2ε=1.68

ηo=4.377,β=0.012

文獻[10]中對標準κ-ε、Realizableκ-ε和RNGk-ε模型進行了比較，認為RNGk-ε模型結合兩層壁面模型的處理，可以有效地模擬大曲率影響彎管湍流流動的問題。

2.3網格劃分和邊界條件

利用Gambit前處理軟件構建模型，Gambit中的求解器使用Fluent5/6，進口設定為velocity_inlet，出口設定為outflow。網格劃分如圖2所示。

圖2 網格劃分示意圖

邊界條件設置有：進口條件為流體的來流速度大小為13m/s，其方向垂直于彎管的縱向截面(XOY平面)；出口條件為采用自由出流條件；壁面條件為壁面上使用無滑移的邊界條件。RNGk-ε模型適合于完全發展的湍流，用在湍流核心區域，但對壁面區域并不適用。采用標準壁面函數法作近壁面處理，可以提高計算效率，有利于工程的實用性，對于模擬各種壁面流動很有效[11]。

3 模擬計算結果與分析

3.1壓力分布

將Gambit劃分的網格輸入至Fluent中，檢查網格質量，變換單位，定義流體的物理性質，設置邊界條件和初始條件。模擬計算得到彎管中心截面(Y=0)上的壓力分布云圖，如圖3所示。

將XOZ平面不同角度徑向方向上的壓力模擬匯集在圖4中。由圖4可知，彎管中徑向壓力的變化是上升的。彎曲段部分，各截面相互間壓力的變化較小。在0～60°截面，內側壓力逐步減小，而外側壓力逐步增大，在60°截面徑向的壓力梯度達到最大。從60～180°截面，內側的壓力逐步增大，外側壓力逐步減小。流體在0°和180°截面的徑向壓力變化曲率相近，且180°截面處的壓力明顯小于0°截面處的壓力。

圖3 管道中心截面壓力分布

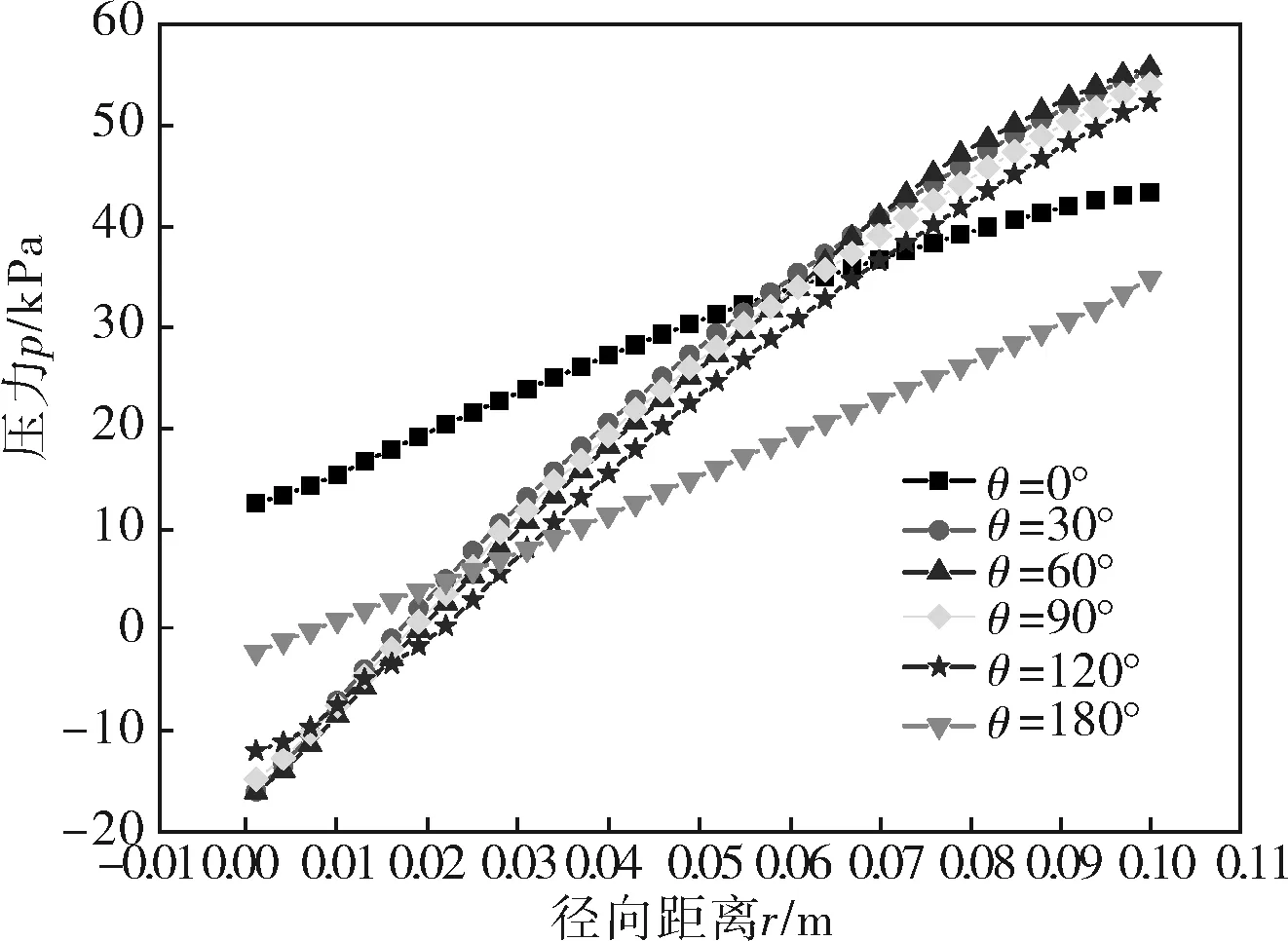
圖4 徑向壓力分布曲線

從圖3的壓力分布云圖也可觀察到，在管道彎曲段內，沿著徑向的壓力梯度變化較大，內壁面附近壓力較小，外壁面附近壓力值較大的現象。這主要是因為流體在流動過程中受管道的彎曲作用，流體向曲率半徑較大的外側壁面流動，而使流體在外側壁面擠壓形成。彎管出口直管段的壓力明顯小于進口直管段處的壓力，其原因是分子粘性致使流體沿管道壁面流動過程中產生的沿程損失和二次流的耗散。

3.2切向速度分布

流體在彎管內流動，速度變化主要是切向速度的變化。流體沿進口直管段進入彎曲部分后，由于受管道彎曲的作用，產生朝向外側的離心力，而產生的離心力使得徑向壓力分布發生變化，呈現出徑向壓力梯度。

將彎管中心XOZ截面不同角度徑向方向上的切向速度值模擬曲線匯集在圖5中，可觀察到：在0°截面，切向速度分布開始發生變化；在0～60°之間，內壁附近切向速度逐步升高，外壁附近的切向速度逐步降低。而流體在60°截面前后切向速度的變化則完全相反；在60～180°之間，內壁附近的切向速度逐步降低，外壁附近的切向速度逐步升高。流體在彎曲段受離心力的影響，內壁附近的切向速度明顯大于外壁附近的切向速度；在180°截面內，彎管外壁附近的切向速度值很接近，但其值高于內側切向速度值，且內壁面附近的切向速度值沿徑向朝內側減小較快。

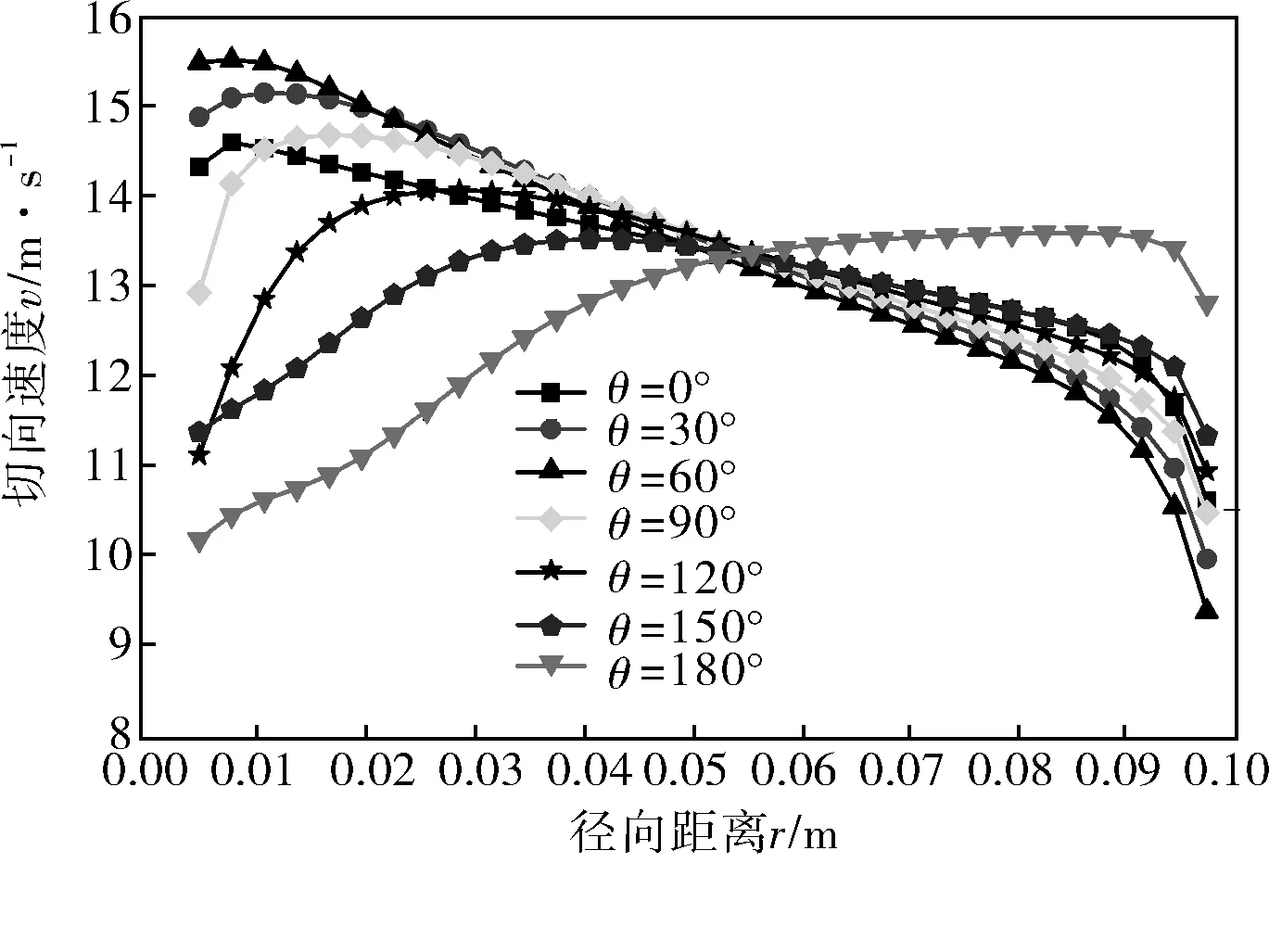
圖5 切向速度分布曲線

流體在彎管的彎曲段，其內部速度和壓力發生著復雜的變化。在0～60°間，外壁面附近壓力升高，內壁面附近壓力降低，而外壁面附近的切向速度降低，內壁面附近的切向速度升高。在流過60°截面附近以后，壓力和速度發生相反的分布規律，外側壓力減小，內側壓力升高，而外側切向速度升高，內側切向速度減小。因此，數值模擬得出的數據與文獻[7]用激光多普勒測速儀測量的實驗結果基本一致。180°彎管內流場的壓力和速度的分布規律與90°彎管相似，180°彎管其轉折點在60°截面，90°彎管在30°截面[12]。

3.3二次流

180°方形截面彎管內的二次流是不可壓縮粘性流體在管道流動的過程中，由于流體的粘性和離心作用在轉彎處橫截面上出現一對旋向相反的漩渦。沿主流方向彎管不同截面的速度矢量圖如圖6所示，可以看到180°方形截面彎管內垂直于主流的二次流的產生與發展過程。從θ=0°截面開始流體由直線流動向旋轉流動轉變，流體的徑向速度指向內側壁面。在θ=30°附近，外壁面附近的壓力此時大于內壁面附近的壓力，使得彎管中心的流體向外側流動，外側壁面附近上半部分的流體向上流動，下半部分的流體向下流動，且上下壁面附近的流體向內擴散，左上角和左下角出現較小的一對二次流。這種二次流漩渦推擠著面內的低速流體順著主流不斷向后發展。到θ=60°，二次流的旋轉中心向彎管內側移動。在θ=90°附近，強烈的二次渦流推擠內側面附近的高速流體流過截面中心位置向外側流動，上壁面和下壁面的低速流體由于二次渦流的帶動，沿壁面向內側面移動，此時截面上兩個渦心繼續向內側壁面且相向移動，表明外側壓力大于內側壓力，使得流體向內側移動。到θ=120°截面，二次流旋轉中心仍然向內側壁面和相向移動。在彎曲段θ=180°處二次流強度達到最大，二次流的旋轉中心位于最內側。

二次流的區域隨著旋轉流動從0°到180°逐漸擴大，強度增強。在出口直管段期間，二次流的渦心逐漸遠離內側向外側移動，同時向彎管中間XOZ平面移動，二次流逐漸衰減直至消失。

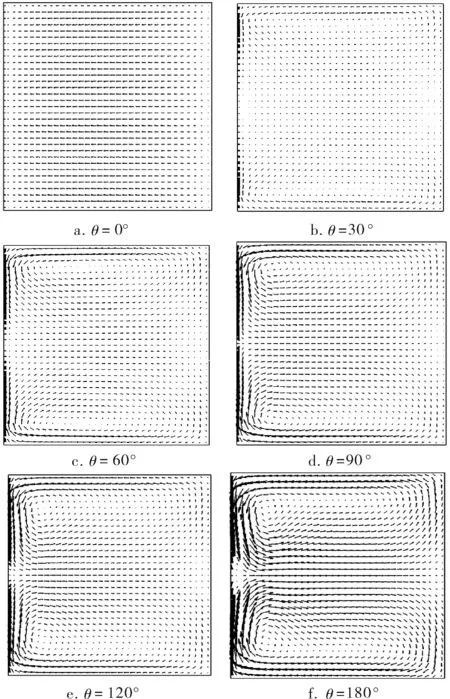
圖6 沿主流方向彎管不同截面的速度矢量圖

4 結束語

運用Fluent軟件，完成對180°方形截面彎管內湍流流動的數值模擬計算，得到彎管內流場的變化規律。在整個彎曲段內，內側壓力低于外側壓力。在0～60°之間，外壁附近壓力升高，切向速度減小，內壁附近壓力降低，切向速度增大；在60～180°之間，外壁附近壓力降低，切向速度增大，內壁附近壓力升高，切向速度減小。同時，還重點分析了管道內二次流的形成和發展過程。這為揭示180°方形截面管道內復雜流動現象的作用機理提供了一定的借鑒。

[1] Dean W R.Note on the Motion of Fluid in a Curved Pipe[J].Phil Mag,1927,4(2):223～238.

[2] Azzola J.Developing Turbulent Flow in a U-bend of Circular Cross-Section[J].Journal of Fluids Engineering,1986,108(2):214～221.

[3] Sudo K,Sumida M,Hibara H.Experimental Investigation on Turbulent Flow in a Circular-Sectioned 90-Degree Bleed[J]. Experiments in Fluids,1998,25(1):42～29.

[4] Taylor A M K P,Whitelaw J H,Yianneskis M.Curved Ducts with Strong Secondary Motion: Velocity Measurements of Developing Laminar and Turbulent Flow [J].Journal of Fluids Engineering,1982, 104(3):350～359.

[5] 江山,張京偉,吳崇健,等.基于FLUENT的90°圓形彎管內部流場分析[J].中國艦船研究,2008,3(1):37～41.

[6] 曾實,Manners A.180°方形彎管中湍流流動的大渦模擬[J].清華大學學報(自然科學版),1999,39(4):100～103.

[7] 徐俊,杜彩虹,王甜,等.180°矩形彎管流場的LDV測量[J].實驗流體力學,2010,24(1):36～41.

[8] 謝俊,郭洪锍,陳煒,等.基于ANSYS和Fluent軟件的導流管流場分析[J].機械設計與制造,2008,9(9):70～72.

[9] Yakhot V, Orszag S A.Renormalization Group Analysis of Turbulence 1.Basic Theory [J].Journal of Scientific Computing, 1986,1(1):39～51.

[10] 丁玨,翁培奮.三種湍流模式數值模擬直角彎管內三維分離流動的比較[J].計算物理,2003,20(5):386～390.

[11] 王福軍.計算流體動力學分析[M].北京:清華大學出版社，2004.

[12] 尚虹,王尚錦,席光,等.90°圓截面彎管內三維紊流場實驗研究[J].航空動力學報,1994,9(3):263～266.

ResearchonInnerFlowCharacteristicsof180°ElbowPipeswithSquareSection

ZHOU Jia, ZHU Mu-cheng, WU Shuai-zhen, LUO Yue-ying, JIA Chuan-wei
(SchoolofManufacturingScience&Engineering,SouthwestUniversityofScience&Technology,Mianyang621010,China)

Aiming at the complex flow characteristics and the secondary flow phenomenon in 180° elbow pipe with square section, the Fluent software was adopted to implement spatial dispersion of continuous equation and Navier-Stokes equation and to simulate and calculate turbulent flow in this 180° elbow pipe. The simulation result shows that this calculation result coincides with the experimental result; and it indicates that both established mathematical model and numerical method are effective; meanwhile, the formation and development of the secondary flow within the elbow pipe were analyzed to obtain the change rules of this secondary flow so as to provide the reference for revealing the mechanism of complex flow in the 180° elbow pipe with square section, and it has a certain significance for both manufacturing and application of mechanical equipment.

180° elbow pipe with square section, Fluent, N-S equation, turbulence flow, numerical simulation, secondary flow

* 國家科技支撐計劃資助項目(2014BAF12B05)。

** 周 佳，男，1990年9月生，碩士研究生。四川省綿陽市，621010。

TQ055.8

A

0254-6094(2016)02-0214-05

2015-06-19)