部分跟蹤與傳遞性

刁素蘭, 曾 鵬, 吳紅英

(1.廣州大學 數學與信息科學學院， 廣東 廣州 510006; 2.懷化學院 數學系, 湖南 懷化 418008)

部分跟蹤與傳遞性

刁素蘭1, 曾 鵬1, 吳紅英2

(1.廣州大學 數學與信息科學學院， 廣東 廣州 510006; 2.懷化學院 數學系, 湖南 懷化 418008)

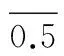
跟蹤性質; 遍歷偽軌; 平均偽軌; syndetic傳遞

0 引 言

設(X,f)是一個拓撲動力系統(簡稱動力系統),是指(X,ρ)是一個緊致度量空間,其中ρ表示X上的一個度量,f:X→X是一個連續滿射. 跟蹤性質在動力系統中扮演著重要的角色.1980年,BLANK[1-2]引進了平均跟蹤性質的概念并證明了某些攝動雙曲系統具有平均跟蹤性質. 自從平均跟蹤的概念問世以來,平均跟蹤性質受到了較多學者的關注[3-7],并且有越來越多新的跟蹤概念出現[5,8-9].

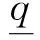
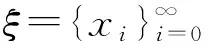
這時,也稱點z,ε-平均跟蹤ξ.

NIU[7]證明，若映射f有平均跟蹤性質且極小點稠密,則f是syndetic傳遞的.

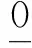
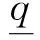
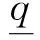
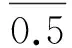
1 預備知識

設(X,f)是一個動力系統.U,V?X,記N(U,V)={i∈Z+:U∩f-i(V)≠φ}.設點x∈X和非空開集U?X,記N(x,U)={i∈Z+:fi(x)∈U}.稱映射f是傳遞的,是指對任意2個非空開集U,V?X,有N(U,V)≠φ.稱映射f是syndetic傳遞的,是指對任意2個非空開集U,V?X,N(U,V)是syndetic的. 稱點x∈X是f的一個極小點,是指對X的任意一個開鄰域U,N(x,U)是syndetic的.f的全體極小點組成的集記為AP(f).

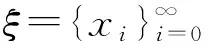
d({i∈Z+:ρ(f(xi),xi+1)<δ})=1.

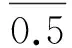
還需要下面的引理.

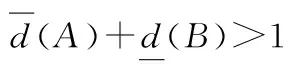
2 主要結果的證明

引理2[12]設(X,f)是一個動力系統.如果映射f是傳遞的并且極小點稠密,則f是syndetic傳遞的.

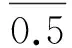
證明 不失一般性,設diamX=1.設U,V是X中的2個非空開集.選取x∈AP(f)∩U,y∈AP(f)∩V,取ε>0,滿足B(x,ε)∈U,B(y,ε)∈V.由于x,y是極小點,則N(x,B(x,ε)),N(y,B(y,ε))是syndetic的.記N1,N2分別是它們的最大間距,令N=N1+N2.由于f是一致連續的,則存在0<δ<ε,滿足當ρ(u,v)<δ時, 對任意n∈{0,1,…,N},有

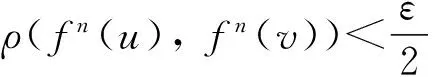
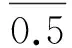
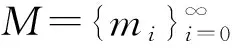
(1)d(M)=0;

其中,M1={0,1,2,…,m1}∪{m2,m2+1,…,m3}∪{m4,m4+1,…,m5}∪…;

其中,m1=1,m2=m1+1,…,mi=mi-1+1.

令ξ1=x,f(x),…,fm1(x);

ξ2=y,f(y),…,fm2-m1(y);

ξ3=x,f(x),…,fm3-m2(x);

ξ4=y,f(y),…,fm4-m3(y)

…

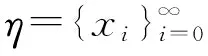
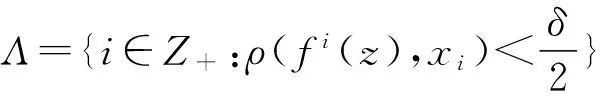
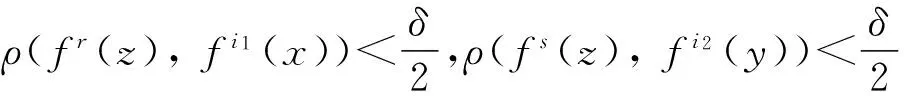
由于x,y是極小點,存在k,l∈{0,1,…,N-1},使得

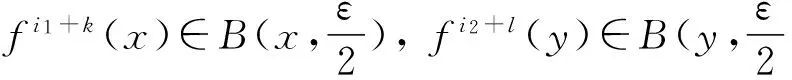
由于f的一致連續性,有

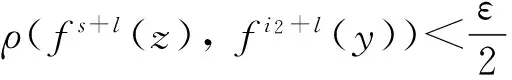
因而

fr+k(z)∈B(x,ε),fs+l(z)∈B(y,ε).

故

fr+k(z)∈B(x,ε)∩f-[(s+l)-(r+k)](B(y,ε))≠?.

因而f是傳遞的.由引理2知,f是syndetic傳遞的.

證明 不失一般性,設diamX=1.設U,V是X中的2個非空開集.選取x∈AP(f)∩U,y∈AP(f)∩V,取ε>0,滿足B(x,ε)∈U,B(y,ε)∈V.由于x,y是極小點,則N(x,B(x,ε)),N(y,B(y,ε))是syndetic的.記N1,N2分別是它們的最大間距,令l=N1+N2.由于f是一致連續的,則存在0<δ<ε,滿足當ρ(u,v)<δ時,對任意n∈{0,1,…,l},有

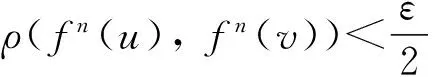
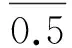
η1=x,f(x),…,f2N-1(x);

η2=y,f(y),…,f2N-1(y).

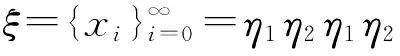
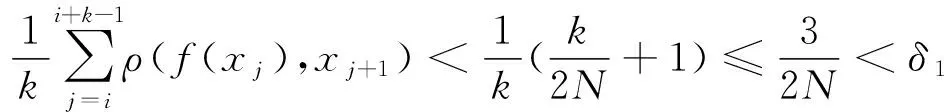
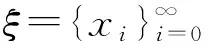
由于x,y是極小點,存在k,m∈{0,1,…,l-1},使得

因為f是一致連續的,因此有

從而

fi1+k(z)∈B(x,ε),fi2+m(z)∈B(y,ε).

所以

fi1+k(z)∈B(x,ε)∩f-[(i2+m)-(i1+k)](B(y,ε))≠?.

因此f是傳遞的. 根據引理2,f是syndetic傳遞的.

3 結 語

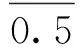
[1] BLANK M L.Metric properties ofε-trajectories of dynamical systems with stochastic be-havior[J]. Ergod Theory Dynam Syst, 1988, 8(3):365-378.

[2] BLANK M L. Deterministic properties of stochastically perturbed dynamical systems (Russian)[J]. Teor Veroyatn Primen, 1988, 33(4): 659-671; Translation in Theory Probab Appl, 1988, 33(4): 612-623.

[3] KULCZYCKI M, KWIETNIAK D, OPROCHA P. On almost specification and aver-rage shadowing properties[J]. Fund Math, 2014, 224: 241-278.

[4] KWIETNIAK D, OPROCHA P. A note on the average shadowing property for expansive maps[J] .Topol Appl, 2012, 159:19-27.

[5] OPROCHA P, DASTJERDI D A, HOSSEINI M. On partial shadowing of complete pse-udo-orbits[J]. J Math Anal Appl, 2013, 404: 47-56.

[6] PARK J, ZHANG Y. Average shadowing properties on compact metric spaces[J]. Commun Korean Math Soc, 2006, 21:355-361.

[7] NIU Y. The average-shadowing property and strong ergodicity[J]. J Math Anal Appl, 2011, 376(2): 528-534.

[8] FAKHARI A, GHANE F H. On shadowing: Ordinary and ergodic[J]. J Math Anal Appl, 2010, 364:151-155.

[9] DASTJERDI D A, HOSSEINI M. Sub-shadowings[J]. Nonlin Anal, 2010, 72: 3759-3766.

[10] 李振宇.q-遍歷跟蹤性質的研究[D].廣州：廣州大學，2015.

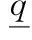
WANG H Y, ZENG P.On partial shadowing of ergodic pseudo-orbits[J].Sci China Math,2016:doi:10.1360/N012014-00256.

[12]WANG H Y, LONG X, FU H M. Sensitivity and chaos of semigroup actions[J]. Semigr Forum, 2012, 84:81-90.

【責任編輯： 周 全】

Partial shadowing property and transitivity

DIAOSu-lan1,ZENGPeng1,WUHong-ying2

(1. School of Mathematics and Information Sciences, Guangzhou University， Guangzhou 510006， China；2. Department of Mathematics, Huaihua University，Huaihua 418008， China)

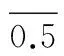
shadowing property; ergodic pseudo-orbit; average pseudo-orbit; syndetic transitive

2015-12-01;

2015-12-23

刁素蘭(1990-)，女，碩士研究生. E-mail：diaosulan168@163.com.

1671- 4229(2016)05-0031-04

O 189.11

A

汪火云, 曾鵬. 平均偽軌的部分跟蹤[J]. 中國科學, 2016:

10.1360/N012014-00256.