面向大數據的淘寶賣家信用度的影響因素分析

麥繼芳, 崔 霞

(廣州大學 經濟統計學院, 廣東 廣州 510006)

面向大數據的淘寶賣家信用度的影響因素分析

麥繼芳, 崔 霞

(廣州大學 經濟統計學院, 廣東 廣州 510006)

消費者在電商平臺上購買商品時，并不能獲得關于消費品的所有信息，只能通過賣家信用、商品圖片和購買評價等指標來判定所選的網店以及商品是否可靠.其中，賣家信用對于消費者的參考尤其重要.對賣家信用度建模能夠在一定程度上保護交易雙方的合法利益，提高交易的成功率.文章基于部分線性可加模型，結合社會資本數據(如新浪微博)，對淘寶賣家信用度進行建模分析：①對數據進行相關分析、異常值剔除、多重共線性消除等預處理;②利用集群Lasso變量選擇方法，識別出對賣家信譽有顯著影響的因素;③對識別出來的因素與賣家信用做簡單線性擬合，得出的結果與實際情況相違背，故又使用廣義可加模型實現對賣家信譽的預測分析.該信用度模型能夠很好地識別刷單賣家，幫助買家防范賣家的欺詐行為.

部分線性可加模型; 大數據; 半參數模型; Lasso;R語言

電子商務的迅速發展給人們的生活帶來了極大的方便.通過網絡和現代物流，人們足不出戶就可以方便購買來自全國各地的各種商品.淘寶網作為B2C電子商務的龍頭老大，憑借其產品的豐富和信譽評價機制的安全優勢，獲得了越來越多在線消費者的信任.然而，由于賣家的逐利性，刷單和刷信譽的行為越來越多.對賣家信用度建模能夠在一定程度上保護交易雙方的合法利益，提高交易成功率.現行使用的信用度評價系統一般采用簡單累加得出賣家的信用度值，過度依賴于好評率，缺少對影響交易其他因素的考慮，如退款率、寶貝數等.另外，目前使用的信用評價系統主要依賴淘寶平臺內部數據，卻未涉及大數據中的社會資本數據.因此，建立有效、實用的網絡購物網站信用評價模型，具有重要的理論意義和現實意義.

電子商務信用的研究還是一個相對較新的領域，文獻[1-2]是國內學者對淘寶網商家信用度評價模型的研究.在國外，中小企業的信用評價是對其品德、聲望、資格、資金實力、擔保以及經營條件等進行分析，來測度違約可能性并且對違約風險進行分類.這種信用評價技術目前主要是依賴于一些統計模型，如線性概率模型、分對數模型和線性判別式分析.國外目前常用的信用評價方法有：5C法等要素法[3]、財務比率綜合分析法、信用度量分析模型[4].

本文基于部分線性可加模型[5]，結合社會資本數據(如新浪微博)，對淘寶賣家信用度進行建模分析.在該模型中設計變量有28個，包括好評率、差評率、退換貨速度、是否為微博達人等.本文探索了影響賣家信用的主要因素及其影響方式，即在模型主要部分中是以線性函數的方式還是非參數函數的方式呈現.當變量個數很多時，可能會包括一些冗余的變量.變量選擇方法能夠去掉冗余變量，精簡模型，從而提高模型預測的準確性和模型的解釋性.

1996年,TIBSHIRANI[6]提出了一種新型的變量選擇方法，即Least absolute shrinkage and selection operator(Lasso).Lasso方法是一種基于懲罰范式的變量選擇方法，與現有變量選擇方法比較， Lasso 不僅能夠準確地選擇出重要變量， 同時還具備變量選擇的穩定性.Lasso方法能夠同時進行變量選擇和參數估計，可適度壓縮參數.文獻[7]探討了Lasso 方法用于高維度、強相關、小樣本的生存資料分析.近年來，有些學者在Lasso算法的改進上做了研究.2004年,EFRON等[8]提出了Least angle regression(Lar)，該算法使得Lasso的計算更加簡單，應用更加廣泛.ZOU等[9]在2005年提出了Elastic Net，該方法能夠更好地處理變量數目p遠遠大于樣本容量n的情形，而且有較好的自變量分組效應.FAN等[10]于2001年提出了SCAD方法，該方法克服了Lasso有偏估計的缺點，改善了其參數估計的一致性和變量選擇一致性. 2011年,何曉群等[11]提出了Adaptive Lasso 方法,該方法的自適應性通過對不同系數采用不同程度的壓縮來實現.

在對本文中的淘寶數據進行分析時，①剔除異常值、進行相關性分析、多重共線性消除等預處理.②對數據使用多元線性回歸模型做擬合，由于變量個數過多，筆者使用了Lasso做變量選擇.遺憾的是，從擬合結果看線性模型擬合這組數據時有一些問題，如賣家信用與關注人數呈負相關,這與現實經驗不相符.③使用部分線性可加模型分析這組數據，并且使用集群Lasso方法對影響賣家信用度的因素進行選擇.從擬合結果看，該模型是充分的.

1 部分線性可加模型

部分線性可加模型是一類應用廣泛的半參數模型[5].其形式：

(1)

其中,Yi為被解釋變量，模型中有p+1個解釋變量{X0i,X1i,…,Xpi}，其中X0i=1；q個解釋變量{Z1i,…,Zqi}.βk是線性部分的未知參數，fk(.)是未知的光滑函數，εi為均值為零的隨機誤差.為了保證模型中未知參數的可識別性，假設E{fk(Zki)}=0.為了方便估計fk(·)，不妨設{Z1i,…,Zqi}的支撐是[0,1].

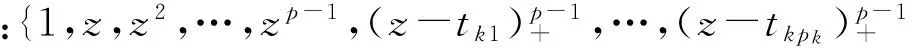
其中，{tkj,j=1,…,pk}是第k個函數展開時所用的節點.

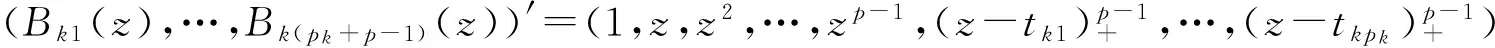
(2)

上述近似模型(2)的集群Lasso估計可以定義為如下極小化問題的解：

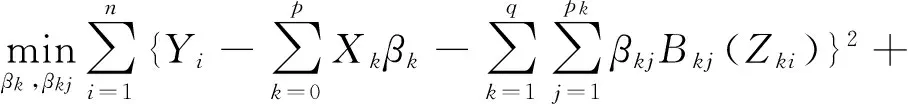
(3)

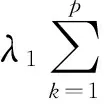
Lasso方法通過選取不同的懲罰參數的值得到不同變量系數的組合，將其反應到圖形中，即得到解路徑，從而看出變量進入活動變量的先后順序，并以此為依據對變量的重要性做出判斷. 模型(3)本質上是一個最優化問題.在Lasso被提出的前幾年，因為缺少對其高效求解的算法，所以一直沒有廣泛流行.直到Lars算法，使得Lasso的求解方便而快捷，從此Lasso相關的方法被廣泛的研究.文獻[8]指出，在一定條件下，Lar算法的解路徑與Lasso的解路徑一致，因而可以通過Lar算法來求解Lasso的解.求解算法大致上有2類，即坐標下降方法(coordinate descent method)和近似梯度方法(proximal gradient method).對于模型(3)的求解直接利用組坐標下降法即可，但是需要2層迭代的結構才行，其中外層迭代為針對λ2懲罰部分的組坐標下降算法，內層迭代為針對λ1懲罰部分的坐標下降算法.而另一種方法，近似梯度算法包括梯度方法、投影梯度法、ISTA算法和著名的稀疏優化問題求解軟件包SLEP(Sparse Learning with Efficient Projections)中的算法基本上都采用了近似梯度方法及其變形來求解.模型(3)中參數λ1,λ2的確定方法主要有交叉驗證、廣義交叉驗證和BIC準則等.本文中采取交叉驗證方法.

2 實證分析

本研究于2015年4月份在淘寶網頁上隨機收集了299個淘寶商家和對應每個商家的新浪微博信息.樣本收集區域覆蓋了14 個省.設淘寶網賣家信用度為因變量Y，協變量包括: 主營占比(X1)、買家信用(X2)、最近半年好評數(X3)、最近半年中評數(X4)、最近半年差評數(X5)、半年前好評數(X6)、半年前中評數(X7)、半年前差評數(X8)、寶貝與描述相符(X9)、賣家服務態度(X10)、賣家發貨速度(X11)、平均退款速度(X12)、近30 d退款率(X13)、近30 d糾紛率(X14)、近30 d處罰數(X15)、月銷量(X16)、寶貝數(X17)、開店時長(X18)、保證金額度(X19)、淘字號(X20)、認證信息(個人或企業)(X21)、微博會員(X22)、微博達人(X23)、關注人數(X24)、粉絲數(X25)、微博數(X26)、活躍天數(X27)和當前等級(X28)等共計28個.其中,X20～X23是定性變量(本文中設為0，1變量)，其他變量為定量變量.

首先刪除信用度過高，表現非常離群的賣家，剩下289個樣本.由于定量變量的單位不盡相同，需對這些變量對應的數據進行標準化處理.

圖1是賣家信用(因變量)的密度函數的圖像，深色線是基于核密度函數估計得到的，灰色圖是基于直方圖得到的.從圖1可見，賣家信用的分布是有嚴重左偏的表現，因而筆者在分析數據時，對因變量做了對數變換，即Y=log(賣家信用).

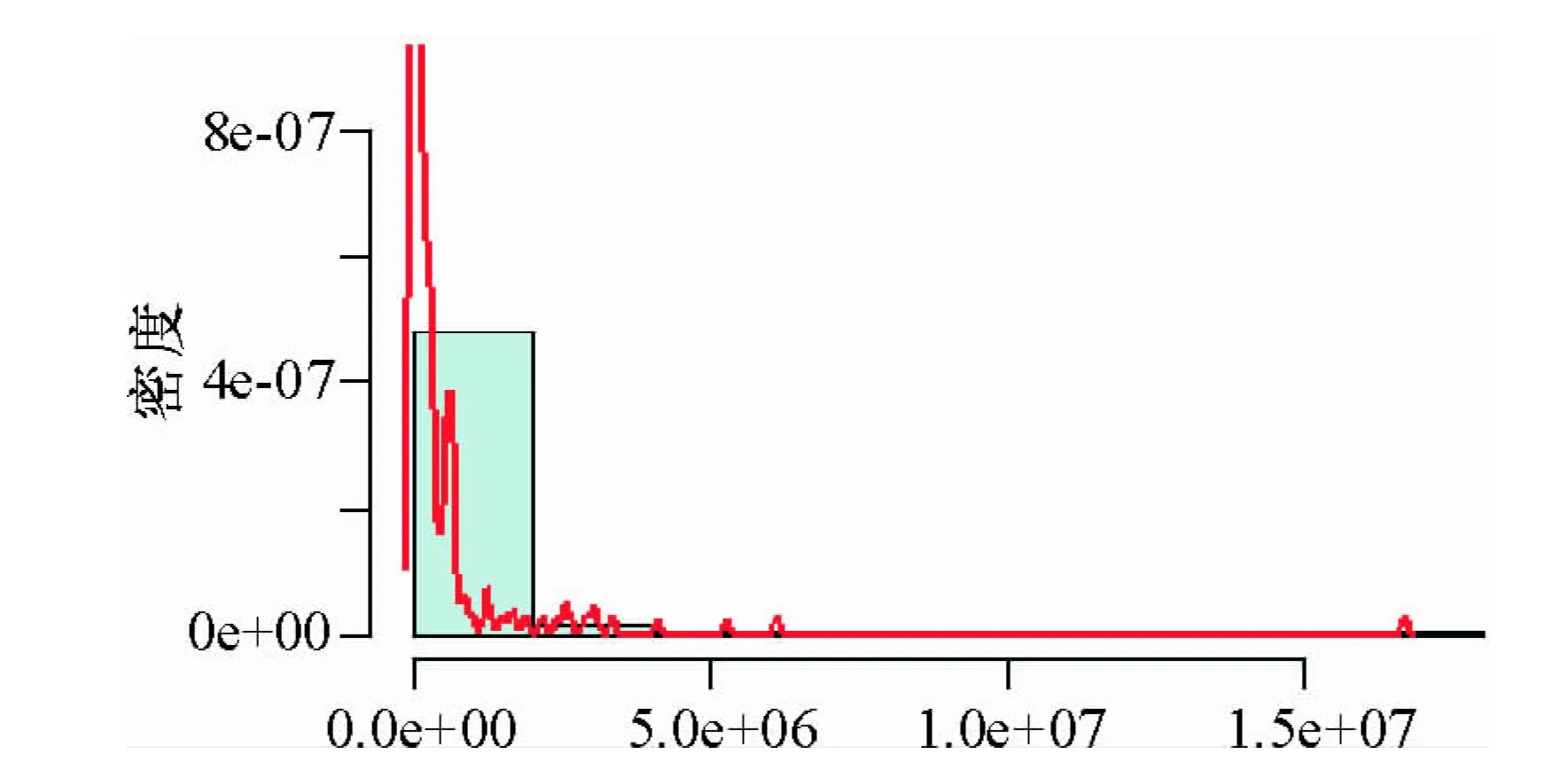
圖1 賣家信用分布情況

使用線性回歸模型對賣家信用與最近半年好評數、賣家信用與半年以前好評數分別進行擬合，結果見圖2，表1和表2.圖2可見,淘寶網計算信用度的規則幾乎完全依賴于賣家信用與最近半年好評數(X3)、半年以前好評數(X6).表1和表2可見，2個模型的決定系數R2分別為0.728和0.987時，調整后的R2分別為0.727和0.987，且F-統計量都很大，分別為751.900、22 070.000，2模型的P值都小于0.05，可見，模型顯著.故只用好評數(最近半年好評數或者半年以前好評數)就可以很好模擬賣家信用.因而，賣家可以通過作弊行為獲得更多的好評數.如果加入好評數變量來建立關于賣家信用的模型，所得結果就不能顯示其他因素對賣家信用的影響.因而在分析數據時，先刪除X3和X6，再構建模型.

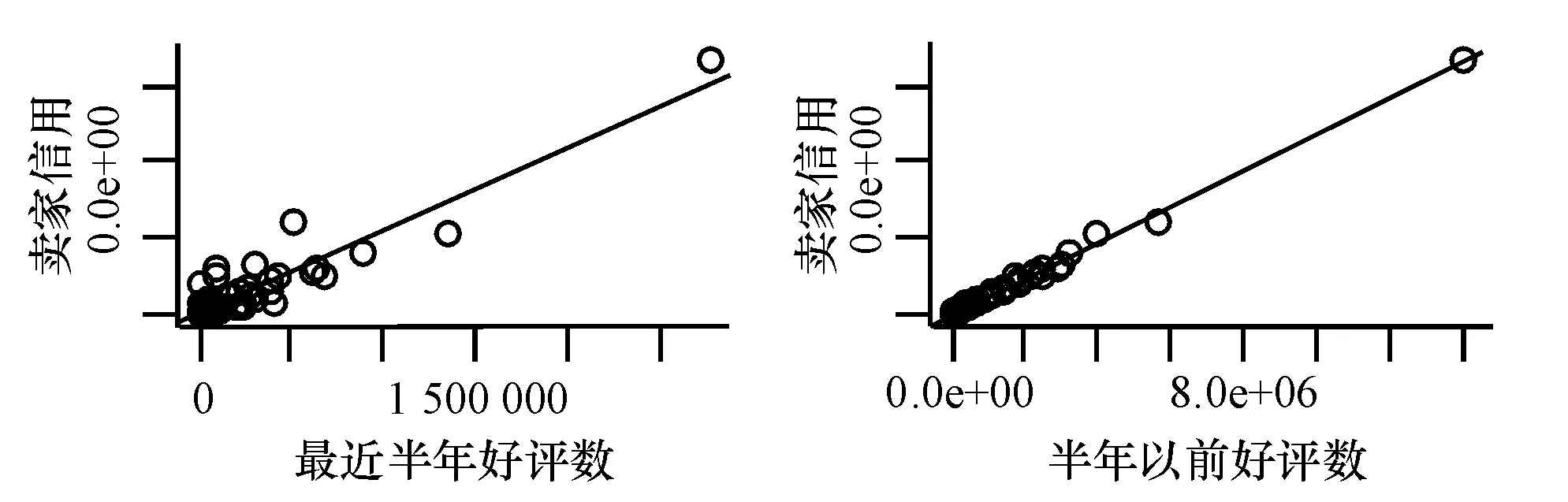
圖2 最近半年好評數和半年以前好評數分別與賣家信用的散點圖

Fig.2 Plots of sellers’s credit and the number of good evaluations

表1 最近半年好評數和半年前好評數分別與賣家信用做線性回歸的結果

Table 1 The linear regression result of the sellers’s credit and the number of good evaluations

模型系數估計值標準誤t值P值1截距54340241802.2480.025*最近半年好評數4.5990.16827.420<2e-16**2截距824452211.5790.115半年以前好評數1.1680.008148.553<2e-16**

顯著準則: 0‘***’ 0.001 ‘**’0.01 ‘*’ 0.05‘.’ 0.1‘ ’1

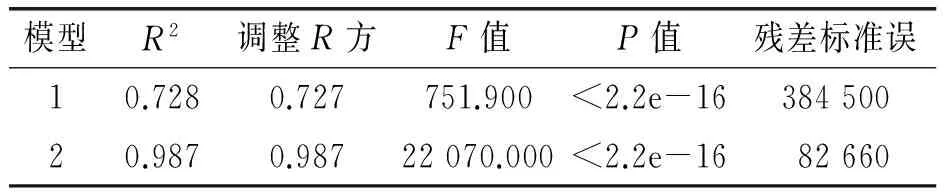
表2 模型的擬合優度檢驗表

若變量之間存在較高的相關性，所得擬合結果的可信度會大大降低.因而，應找出變量與變量之間相關性較高的變量，將它們劃分為一組，再從各組中找出一個代表性變量(各組中對賣家信用影響最大的因素).我們計算了所有變量的相關系數矩陣，發現“賣家服務態度”、“賣家發貨速度”、“寶貝與描述相符”之間的兩兩相關系數超過了0.9，故剔除了變量“賣家服務態度”；另外，微博數據中的“活躍天數”和“當前等級”的相關系數高達0.97，因而刪除了“當前等級”.數據經過上面的預處理，最后剩下24個的變量.其中包括4個定性變量和20個定量變量.

首先使用線性模型對這組數據進行分析，并且使用R軟件中的程序包Matrix，Grpreg和Ncvreg進行變量選擇和擬合.最后輸出的結果就會得到Lasso方法的解路徑[6],見圖3.

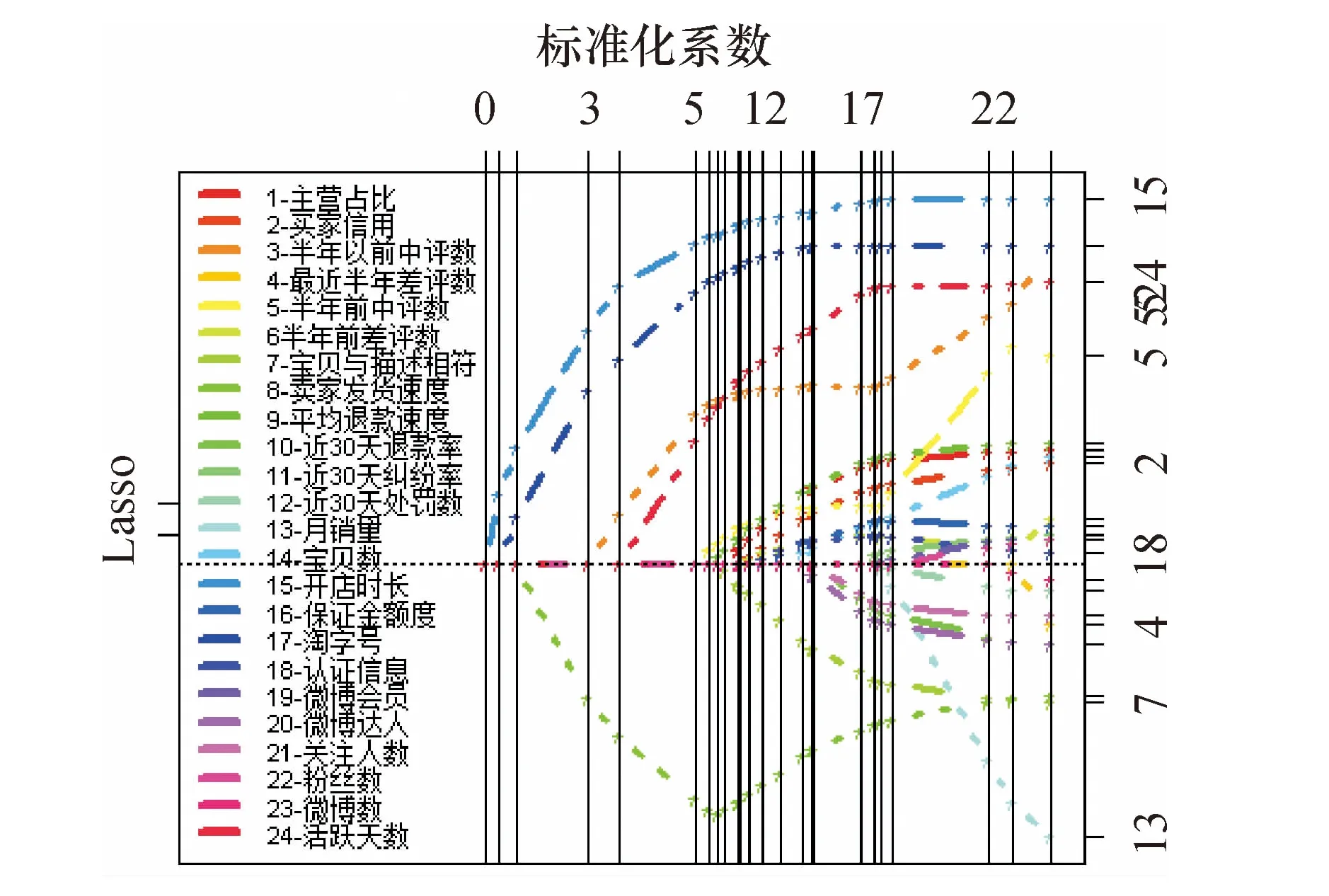
圖3 解路徑圖

且各變量的系數估計見表3.

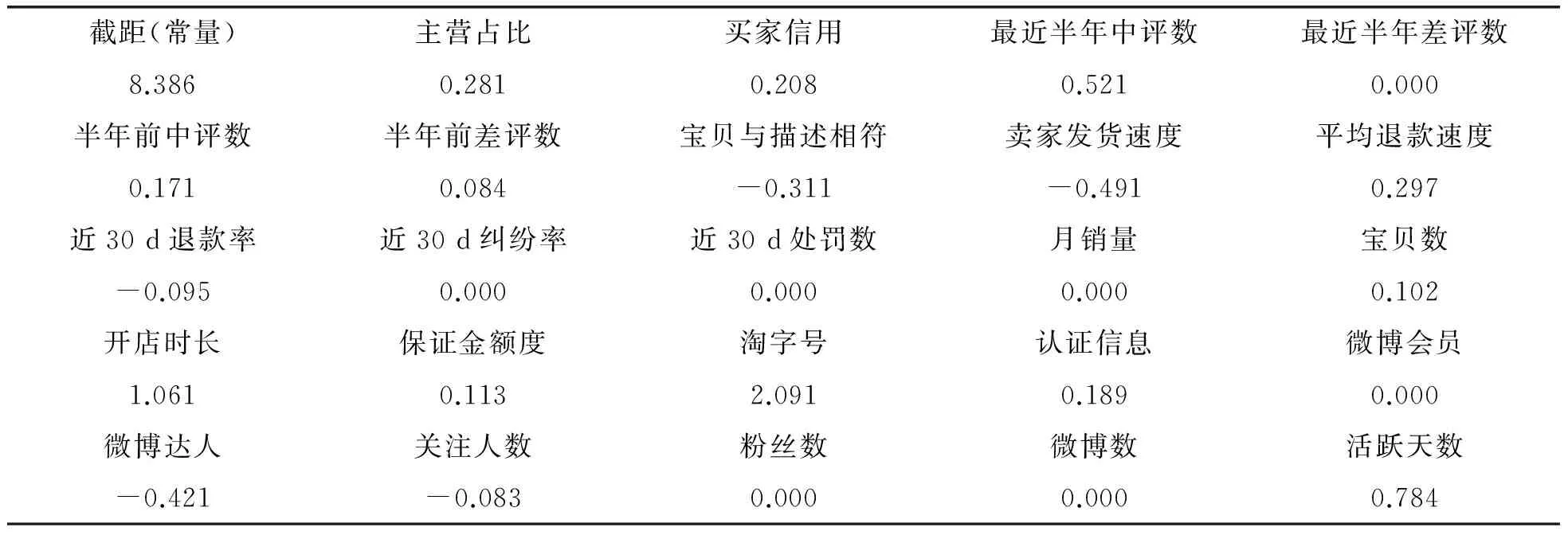
表3 24個變量對應的系數

圖3和表3可見，最近半年差評數、近30 d糾紛率、近30 d處罰數、月銷量、粉絲數、微博會員和微博數等7個變量的系數都為零,故只剩下17個變量,分別為主營占比、買家信用、最近半年中評數、半年前中評數、半年前差評數、寶貝與描述相符、賣家發貨速度、平均退款速度、近30 d退款率、寶貝數、開店時長、保證金額度、淘字號、認證信息、微博達人、關注人數和活躍天數.

利用統計軟件R語言將這些變量與Y進行簡單的線性擬合，所得回歸分析結果分析見表4.

表4反映了置信水平在0.05以下的顯著變量有8個，分別為：主營占比、買家信用、最近半年中評數、平均退款速度、開店時長、淘字號、微博達人和活躍天數；此時的殘差標準差為1.885，R2為0.749，調整的R2為0.734，F值較大，P值很小.然而以上結果反映了賣家信用與微博達人和關注人數呈負相關,這與現實經驗不相符.

為了改善線性模型的擬合結果，筆者采用如下部分線性可加模型：

賣家信用=β0+β1*淘字號+β2*認證信息+β3*微博會員+β4*微博達人+f1(主營占比)+f2(買家信用)+f3(最近半年中評數)+f4(最近半年差評數)+f5(半年以前中評數)+f6(半年以前差評數)+f7(寶貝與描述相符)+f8(賣家發貨速度)+f9(平均退款速度)+f10(近30 d退款率)+f11(近30 d糾紛率)+f12(近30 d處罰數)+f13(月銷量)+f14(寶貝數)+f15(開店時長)+f16(保證金額度)+f17(關注人數)+f18(粉絲數)+f19(微博數)+f20(活躍天數)+ε(其中E(ε|X)=0).

筆者使用統計軟件R軟件中的“mgcv”包實現部分線性可加模型擬合，所得回歸分析結果見表5.

表4 回歸分析結果

自由度為271的殘差標準誤=1.885;多元R2=0.749；調整R2=0.734;自由度是17和271的F值=47.65；P值<2.2e-16.

顯著準則: 0‘**’ 0.001 ‘**’0.01 ‘*’ 0.05‘.’ 0.1‘ ’1.

表5可見,置信水平在水平0.05下時,顯著的變量總共10個,其中線性部分有4個,分別是淘字號、 近30 d退款率、月銷量和活躍天數；非參數部分有6個，分別為主營占比、最近半年中評數、賣家發貨速度、平均退款速度、寶貝數和開店時長.上面結果顯示調整R2=0.877,調整R2=0.895，說明模型有良好的解釋能力.另外,部分線性可加模型得到的結果與簡單線性模型相比更符合現實情況.比如說，對商家信用度有影響的因素——開店時長.開店的時間長短能反映出商家的信譽好壞，反過來，只有商家信譽好，得到顧客的信賴，店家才能長期地經營下去.因此,建議購買者在網上購買商品時，可以通過參考開店時間這個指標來判斷哪家商品質量更加可靠，這樣更容易在網上淘到滿意的商品.當然，除了開店時長，還可以參考月銷量、寶貝數、店家新浪微博、活躍天數和店家是否有淘字號等指標來判斷哪個商家最可靠，而不像以往那樣僅僅參考好評數而被商家欺騙.

表5 部分線性可加模型回歸分析結果

Table 5 The partically linear additive model regression analysis

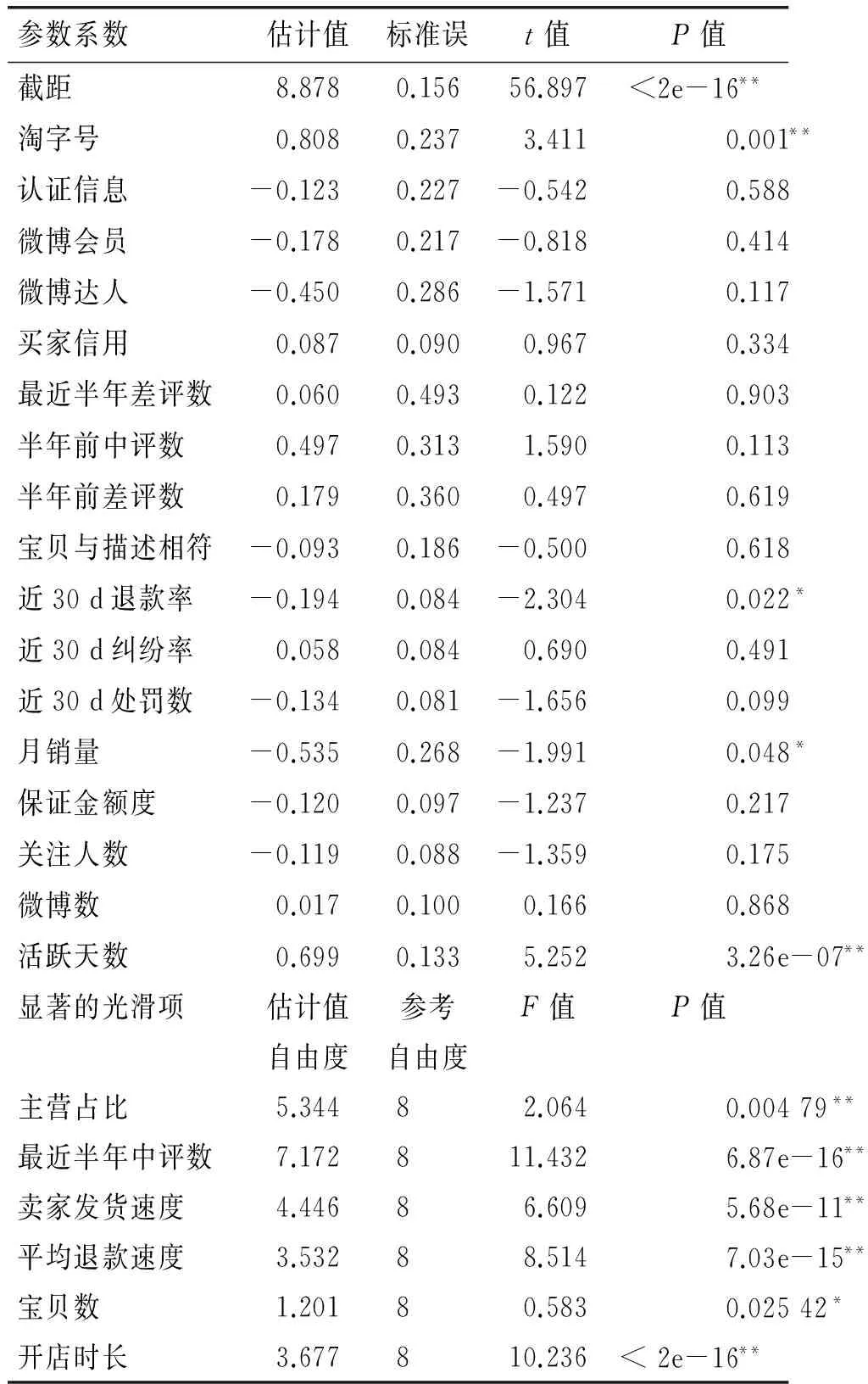
參數系數估計值標準誤t值P值截距8.8780.15656.897<2e-16**淘字號0.8080.2373.4110.001**認證信息-0.1230.227-0.5420.588微博會員-0.1780.217-0.8180.414微博達人-0.4500.286-1.5710.117買家信用0.0870.0900.9670.334最近半年差評數0.0600.4930.1220.903半年前中評數0.4970.3131.5900.113半年前差評數0.1790.3600.4970.619寶貝與描述相符-0.0930.186-0.5000.618近30d退款率-0.1940.084-2.3040.022*近30d糾紛率0.0580.0840.6900.491近30d處罰數-0.1340.081-1.6560.099月銷量-0.5350.268-1.9910.048*保證金額度-0.1200.097-1.2370.217關注人數-0.1190.088-1.3590.175微博數0.0170.1000.1660.868活躍天數0.6990.1335.2523.26e-07**顯著的光滑項估計值自由度參考自由度F值P值主營占比5.34482.0640.00479**最近半年中評數7.172811.4326.87e-16**賣家發貨速度4.44686.6095.68e-11**平均退款速度3.53288.5147.03e-15**寶貝數1.20180.5830.02542*開店時長3.677810.236<2e-16**

調整R2=0.877；離差解釋能力=89.5%；廣義交叉驗證值=1.926；尺度參數=1.637；n=289.

顯著準則: 0‘**’ 0.001 ‘**’0.01 ‘*’ 0.05‘.’ 0.1‘ ’1.

模型可以精簡為

賣家信用=8.878 41+0.807 87*淘字號-0.194 05*近30 d退款率-0.534 52*月銷量+0.699 13*活躍天數+f1(主營占比)+f2(最近半年中評數)+f3(賣家發貨速度)+f4(平均退款速度) +f5(寶貝數)+f6(開店時長) +ε.

以下為非參數部分相應函數的擬合及其置信帶的圖(圖4).

圖4可見，非參數部分中“主營占比” 呈現上下波動的形式； “最近半年中評數”先呈現上下波動，后呈現上升的趨勢；“賣家發貨速度”是先上升后下降，再上升，最后呈現下降的趨勢；“寶貝數”對賣家信用的影響是上升的趨勢；而“平均退款速度”和“開店時長”是先上升后下降的趨勢.

圖4 非參數部分相應函數的擬合及其置信帶

圖5是擬合后的殘差結果.

圖5 擬合值

部分線性可加模型殘差圖的點的分布比較均勻，沒有明顯的趨勢，與線性模型相比，擬合效果有明顯的提高.

3 結 論

基于淘寶網信息和淘寶商家的新浪微博信息，本文使用部分線性可加模型，深入探討了對淘寶賣家信用度的影響因素，發現對淘寶信用度有顯著影響的因素有10個.其中，與賣家信用呈線性關系的變量是淘字號、 近30 d退款率、月銷量和活躍天數；呈非線性的變量是主營占比、最近半年中評數、賣家發貨速度、平均退款速度、寶貝數和開店時長.由此，可以知道影響淘寶買家信用的因素：主營占比、最近半年中評數、賣家發貨速度、平均退款速度、寶貝數、開店時長、淘字號、 近30 d退款率、月銷量和活躍天數.因此，建議顧客在網上購物時可以通過參考商家的這些指標，去判斷哪個商家更加可靠.例如，如果顧客要買的商品在該家淘寶店的主營占比較大，該商家開店時間較長，且有淘字號的標志、寶貝數較多和保證金額較高等特征，那么可以認為該商家信用度較好，可以考慮在該商店購買該商品.

此外，活躍天數這個變量對賣家信用有正的影響，近30 d退款率有負的影響.由此可見，如果該淘寶商家的新浪微博的上線活躍次數較多，說明賣家服務更加周到，也更加靠譜.如果該店鋪退款率較少，可以推測商品質量較好，得到顧客的認可，因此，該賣家的信用度也會相對較高.

本文所研究的方法和思路雖然比較科學，但也有需要改進的空間.例如，需要擴大對淘寶商家信用度有影響的因素范圍和綜合考慮買家的評論內容等.另外,因為買家評論雖然對賣家信用有一定的影響，但難保沒有作假的可能，所以也應對這個因素做一些處理.

為更深入地挖掘淘寶賣家信用的影響因素，只是收集一次數據是不夠的.在未來的研究中，計劃按月份跟蹤收集相關淘寶賣家的數據，使用縱向數據模型分析該組數據.隨著數據的豐富，所得研究結果會更可靠.

[1] 吳培紅.淘寶網賣家信譽影響因素研究[D].天津: 河北工業大學，2011.

WU P H. The research of taobao sellers’ reputation affecting factors[D]. Tianjin: Hebei University of Technology, 2011.

[2] 劉博.淘寶網商的信用評價模型研究[D].北京：對外經濟貿易大學，2009.

LIU B. The research of taobao credit evaluation model[D]. Beijing: Foreign Economic and Trade University,2009.

[3] 孔松泉.基于銀行微觀信貸風險管理的理論與方法研究[D].南京：東南大學，2002.

KONG S Q. Study on the theory and method of the micro credit risk management of banks[D]. Nanjing: Southeast University, 2002.

[4] 陳珺.基于灰色多層次評價方法的中小企業信用評級研究[D].南昌：南昌大學，2010.

CHEN J. On the multi-level gray evaluation method of the small and medium-sized enterprise credit rating research[D]. Nanchang: Nanchang University, 2010.

[5] CUI X, WEN S Q, PENG H, et al. Component selection in the additive regression model[J]. Scandin J Stat, 2013, 40(3): 491-510.

[6] TIBSHIRAN R. Regression shrinkage and selection via the lasso[J]. J Royal Stat Soc Ser B,1996,58(1): 267-288.

[7] 閆麗娜，覃婷，王彤. LASSO 方法在 Cox 回歸模型中的應用[J]. 中國衛生統計，2012, 29(1):58-64.

YAN L N, QIN T, WANG T. The application of Lasso method in the Cox regression model[J]. China Health Stat, 2012,29(1).

[8] EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J].J Math Stat, 2004, 32(2):407-499.

[9] ZOU H, TREVOR H. Regularization and variable selection via the elastic net[J].J Royal Stat Soc, 2005,67(2):301-320.

[10]FAN J, LI R. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. J Am Statist Ass, 2001, 96(456): 1348-1360.

[11]何曉群，劉文卿.應用回歸分析[M].3版. 北京：中國人民大學出版社，2011.

HE X Q, LIU W Q. The application of regression analysis[M]. 3rd ed. Beijing: Chinese University Press, 2011.

[12]MAMMEN E, VAN D G S. Penalized quasi-likelihood estimation in partial linear models[J]. Ann Statist, 1997,25(3): 1014-1035.

【責任編輯： 陳 鋼】

Taobao sellers credit evaluation based on mass data

MAIJi-fang,CUIXia

(School of Economic & Statistics, Guangzhou University, Guangzhou 510006, China)

In this paper, we model the credit of Taobao seller based on the partially linear additive model and social communication data (such as Sina weibo). To control the impact of “good evaluation”, we do not use it in our model. First, we delete the noisy data and the related variables which result in multicollinearity. A natural choice is to use linear model to fit the data, however, we find that linear model is not adequate. Then we apply the partially linear additive model to analyze the data, and it indicates that this model performs better than traditional linear model.

partially linear additive model; mass data; semiparametric model; Lasso; R language

2016-05-03;

2016-05-16

麥繼芳(1991-)，女，碩士研究生.E-mail:1542178467@qq.com

1671- 4229(2016)05-0035-07

O 212

A