病態矩陣參數估計的改進主元加權迭代算法
潘 軼,岳建平,劉 斌
(1.河海大學 地球科學與工程學院,江蘇 南京 210098)
病態矩陣參數估計的改進主元加權迭代算法
潘 軼1,岳建平1,劉 斌1
(1.河海大學 地球科學與工程學院,江蘇 南京 210098)

傳統測繪數據處理中矩陣求逆的準確性極大地影響最終解算精度。針對測量數據處理常遇到的病態矩陣求逆不穩定,導致精度顯著降低等問題,提出一種改進的主元加權迭代法的病態矩陣處理算法。該算法結合傳統主元加權迭代法精度高、誤差轉移法穩定性好的優點,先將誤差從解向量轉至中間變量,再利用主元加權迭代法求解中間變量,實現更高精度的解算結果。實驗表明,改進算法在良態矩陣法方程中解算結果與傳統方法一致,在病態矩陣中改進算法精度更高。
參數估計;病態矩陣;改進主元加權迭代;誤差轉移
一直以來,病態問題存在于測繪領域的方方面面,比如控制網平差、坐標轉換、GPS快速定位計算、形變分析、大地測量反演、衛星重力向下延拓、航天飛行器的精密軌道解等[1]。在這些測量數據的處理中,病態矩陣求逆的不穩定性導致最終解算精度顯著降低,該問題亟待解決。針對測繪領域中的病態問題,國內外學者做過一系列研究,并取得相應成果。王樂洋等[2]采用嶺估計法處理加權總體最小二乘平差的病態性問題;郭海濤等[3]提出利用廣義嶺估計解決單線陣CCD衛星影像外方位元素解算中法方程病態問題,該方法簡便、穩定;Gui Q M等[4]提出基于奇異值分解的有偏估計,并將其應用于大地測量病態問題中;Wang Z[5]先基于Tikhonov正則化法選擇合適的正則化矩陣R 削弱法方程病態,再結合 Lambda方法確定整周模糊度,得到一種解決單頻接收機快速定位系統中病態問題的新算法。Vajargah等[6]利用遺傳算法找到2個可逆對角陣,并將其條件數縮放至最小,降低病態程度。王永弟等[7]先使用主元加權進行預處理,再構造迭代公式迭代處理病態問題,大大提高解的精度。胡圣榮等[8]提出了誤差轉移法,將誤差從解向量轉移到中間變量,提高解的精度與穩定性。
本文將誤差轉移法與主元加權迭代法相結合,研究了一種新算法。在矩陣分別為良態和病態情況下,將其應用效果與其他算法如高斯約化法、傳統主元加權迭代法進行對比分析,得出結論。
1 改進主元加權迭代法原理
1.1 傳統主元加權迭代法
一般情況下,參數估計線性化后的方程組的形式如下:

式中,A為系數矩陣;b為常數項;x為所求解向量。若令α為權因子,E為n階單位矩陣,則傳統主元加權法將式(1)左右兩端各加上ax,得:

通常根據條件數的大小衡量線性方程組的病態程度:系數矩陣A的條件數越大,方程組病態程度越大。根據文獻[9]可得,對于正定對稱矩陣A,當α>0時,則cond(A+αE)<cond(A)。其中cond表示條件數。將式(1)變換為式(2),減小了條件數,從而減輕了線性方程組的病態程度。
因式(2)兩端都含有解x,可構造迭代公式:
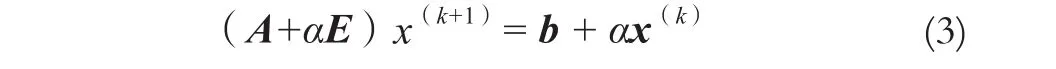
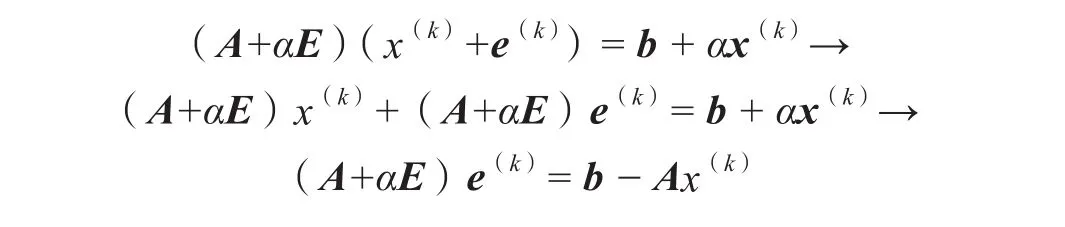
1.2 改進主元加權迭代法
傳統主元加權迭代法精度已經很高,為了進一步提高解算結果的精度與穩定性,本文在傳統主元加權迭代法的基礎上引入誤差轉移法,得到一種新的病態矩陣處理算法——改進主元加權迭代法。顯然,對病態方程組 Ax = b直接求解時,解x誤差太大。本文算法先引入C,變換式(1),得到:

其中,C為n×n非奇異矩陣。根據式(4),求解出的解向量y誤差雖大,但通過式(5)能夠得到誤差很小的解x:

簡而言之,這一步驟將誤差體現在中間變量y上而避開解x,即將解x的誤差轉移到y上,提高了解x的精度。文獻[6]中取C = AT實際效果較好。再在變換后的方程組式(4)左右兩端各加上αx,得:
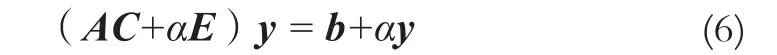
再根據迭代公式
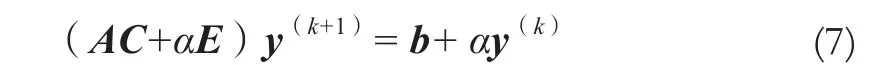
求解,得到中間變量y。最后通過式(5)得到更精確的解x。
本文結合誤差轉移與主元加權迭代法,得到一種改進的主元加權迭代法。即先將x替換為Cy,利用主元加權迭代法求解ACy = b,得到中間向量y;再由x=Cy得到解x。該方法在主元加權迭代法的基礎上,加入誤差轉移,進一步提高了解的精度與穩定性。該方法在Mmatlab中的解算步驟如下:
1)選取C,變換Ax=b為ACy=b;
2)選取α,選取初始點y(0),利用三角分解法求解(AC+αE)y(1)= b+ αy(0),得到y(1);
3)進入循環,計算r(k)= b - AC y(k);
4)求解(AC+αE)e(k)= r(k);
5)計算y(k+1)= y(k)+e(k);
7)計算x=Cy,得到解向量x。該方法的流程圖如圖1所示。
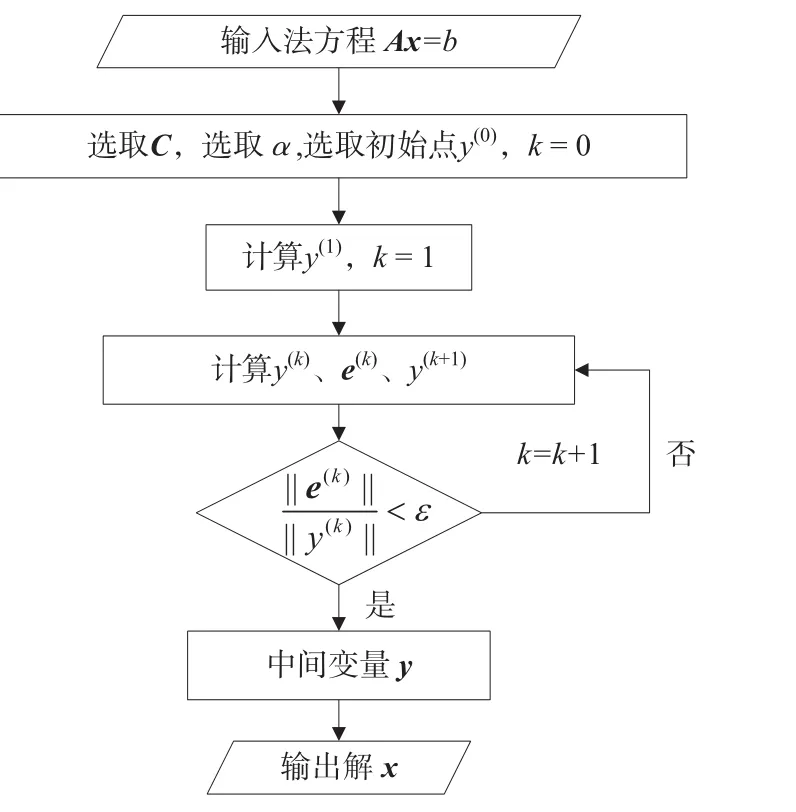
圖1 改進主元加權迭代法
2 算例分析
下面就各方程組分別為良態和病態2種情況下,利用高斯約化法、主元加權迭代法、改進主元加權迭代法3種方法進行求解,并對解的結果進行對比分析。
2.1 良態線性方程組求解
某三角網坐標平差的法方程如式(8)所示[10]:

式(8)的系數矩陣A的條件數為2.714 7,該線性方程組為良態方程組。利用高斯約化法、主元加權迭代法、改進主元加權迭代法3種方法分別對其進行求解,計算結果如表1所示。
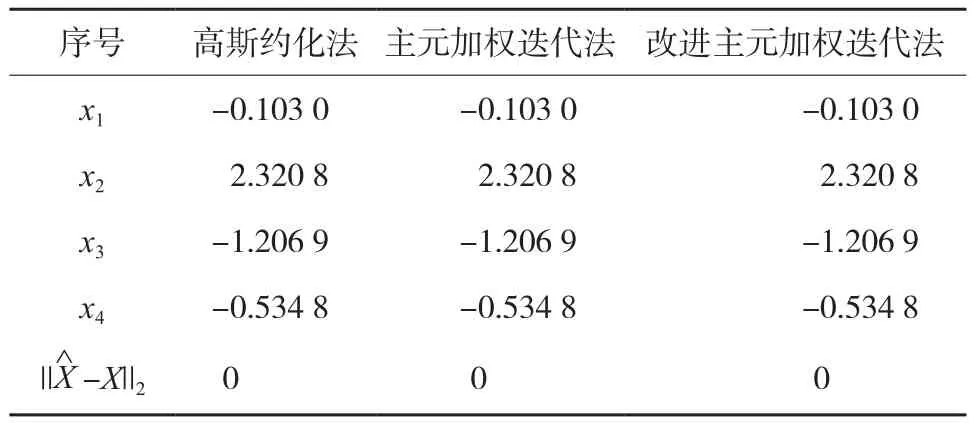
表1 計算結果
由表1中的計算結果可知,當線性方程組為良態時,無論是主元加權迭代法,還是本文中的改進主元加權迭代法,計算結果都與高斯約化法相同。
2.2 病態線性方程組求解
為了證明本文方法的通用性,選取文獻[11]中一個例子:
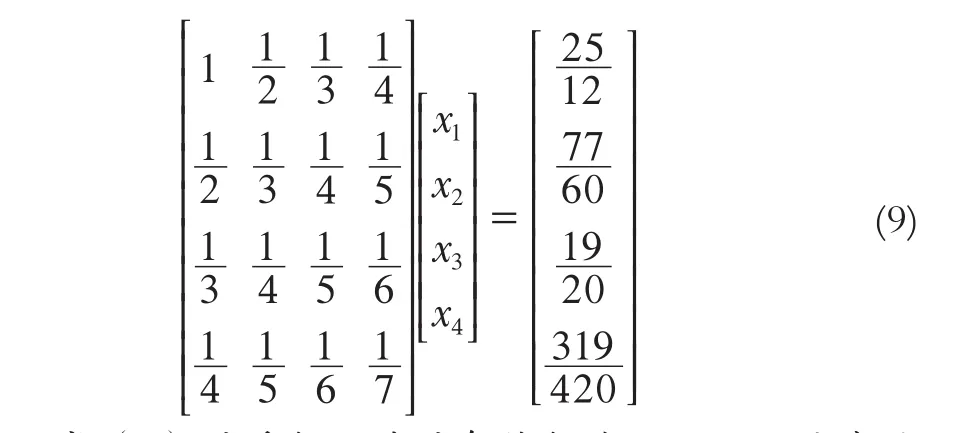
其中,式(9)的系數矩陣的條件數為15 514,該線性方程組為病態方程組。本例的精確解為[x1x2x3x4]T= [1 1 1 1]T。對常數項進行擾動,取為[2.083 3 1.283 3 0.950 0 0.797 5]T。利用高斯約化法、主元加權迭代法、改進主元加權迭代法3種方法對方程組(9)進行求解,計算結果如表2所示。
由表2中的計算結果可知,當線性方程組為病態時,高斯約化法、主元加權迭代法、改進加權迭代法3種方法參數真值與估值之差的范數分別為 202.000 0、0.186 7和0.117 5。相對于高斯約化法,利用主元加權迭代法與改進加權迭代法得到的計算結果精度大大提高;相對于主元加權迭代法,使用本文中的改進主元加權迭代法獲得的計算結果精度更高。
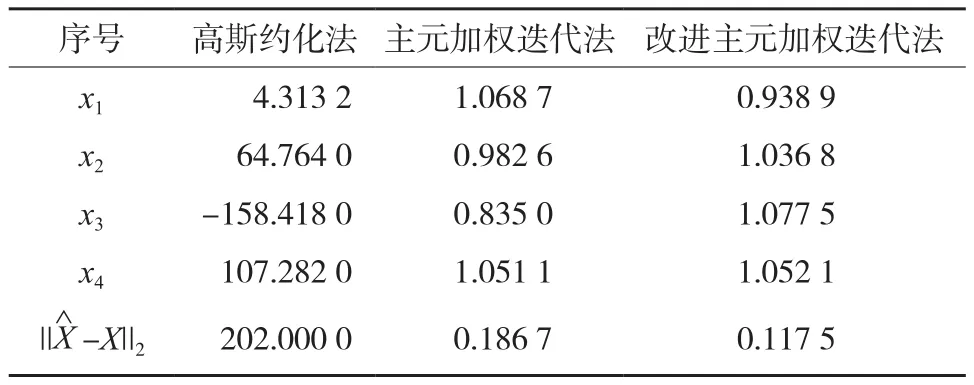
表2 計算結果1
為了進一步證明本文方法在測量數據處理中的作用,再選取文獻[12]中一個例子。該算例的設計陣與觀測值如表3所示。
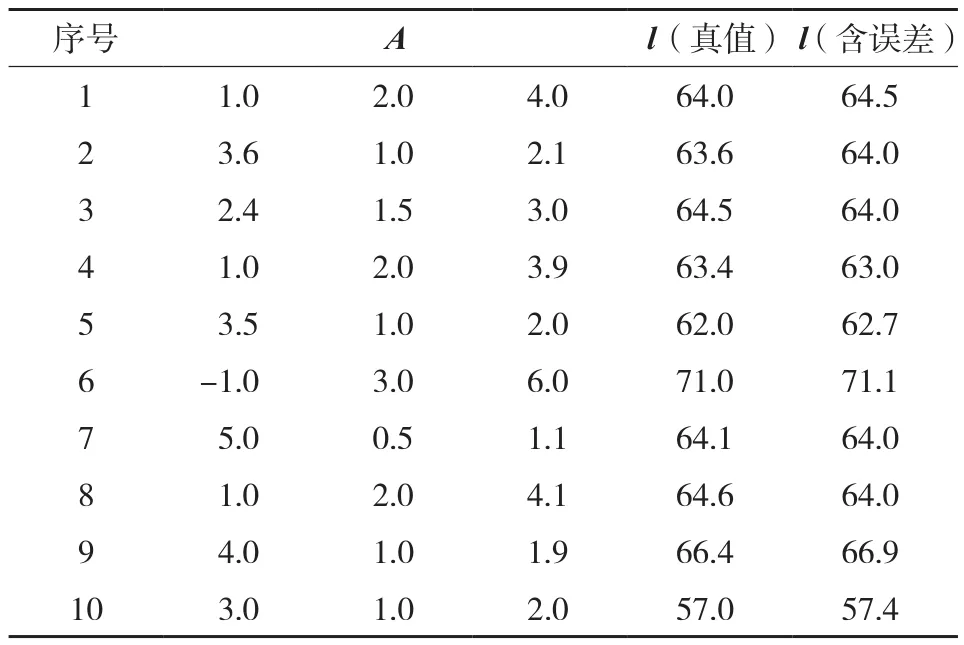
表3 設計陣與觀測值
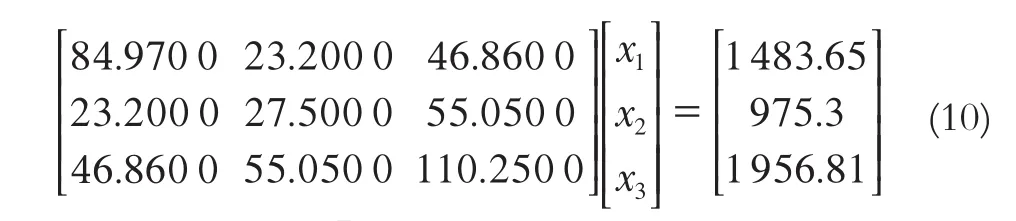
其中,法矩陣ATA的條件數為1.794×104,易得ATAx=ATl為嚴重病態線性方程組。該病態線性方程組有3個未知數,其精確解為
利用高斯約化法、主元加權迭代法、改進主元加權迭代法3種方法對病態線性方程組ATAx=ATl進行求解,計算結果如表4所示。
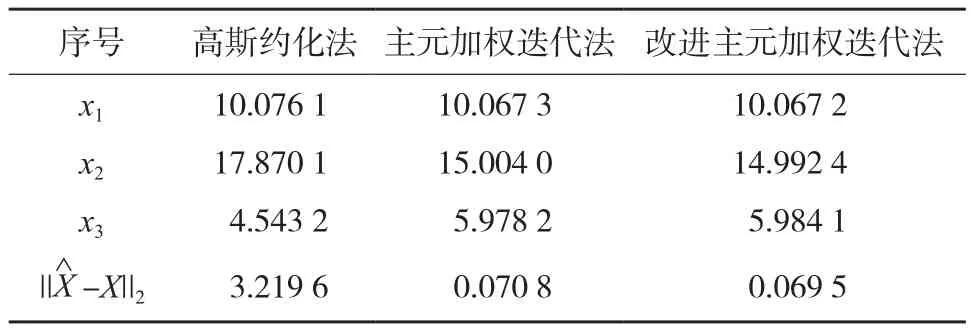
表4 計算結果2
由表4中的計算結果可知,當線性方程組為病態時,高斯約化法、主元加權迭代法、改進加權迭代法3種方法參數真值與估值之差的范數分別為3.219 6,0.070 8和0.069 5。相對于高斯約化法,利用主元加權迭代法與改進加權迭代法得到的計算結果精度得到較大提高;相對于主元加權迭代法,使用本文中的改進主元加權迭代法獲得的計算結果精度更高。
通過以上3個算例可得,無論是在線性方程組為良態還是病態時,利用改進主元加權迭代法求解的結果都非常接近真值。相對于傳統算法,本文中的主元加權迭代法的求解精度有一定的提高。
3 結 語
病態模型的求解一直是測繪領域中常常遇到的問題。相對于傳統算法,本文提出一種改進主元加權迭代法,并分別在方程組為良態和病態時,將其應用效果與高斯約化法、主元加權迭代法進行對比分析。計算結果表明,本文算法適用性強、求解精度高。但本文只將該算法與個別算法進行比較,與其他算法的對比還有待研究。
[1] 王振杰,歐吉坤.大地測量中不適定問題的正則化解法研究[D].北京:中國科學院研究生院,2003
[2] 王樂洋,許才軍,魯鐵定.病態加權總體最小二乘平差的嶺估計解法[J].武漢大學學報(信息科學版),2010,35(11):1 346-1 350
[3] 郭海濤,張保明,歸慶明.廣義嶺估計在解算單線陣CCD衛星影像外方位元素中的應用[J].武漢大學學報(信息科學版),2003,28(4):444-447
[4] GUI Q M, GUo J F, oU J K. Biased Estimation Based on SVD and Its Application in Geodetic Adjustment[J].Bollettino di Geodesia e Science Aiffni,2002(61):99-106
[5] WANG Z. A New Approach to Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers (IoN GPS/GNSS 2003) [A]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation [C]. Portland, oR: oregon Convention Center, 2003. 1 229-1 239
[6] VAJARGAH B F, MoRADI M. Diagonal Scaling of Ill-Conditioned Matrixes by Genetic Algorithm[J]. Journal of Applied Mathematics, Statistics and Informatics,2012, 8(1):49-53
[7] 王永弟,趙好好.病態線性模型參數估計的主元加權迭代法[J].測繪通報,2014(2):23-25
[8] 胡圣榮,羅錫文.病態線性方程組的新解法:誤差轉移法[J].華南農業大學學報,2001,22(4):92-94
[9] 唐麗,李鵬飛.主元加權迭代法求解病態線性方程組[J].科學技術與工程,2012,12 (2):381-383
[10] 武漢測繪科技大學測量平差教研室.測量平差基礎[M].北京:測繪出版社,1996
[11] HoFMANN B, MAT P. SomeNote on the Modulus of Continuity for Ill-posed Problems in Hilbert Space [J]. Weierstra? Institute for Applied Analysis and Stochastics, 2011, 16(6):34-41
[12] 周江文,黃幼才.抗差最小二乘法[M].武漢:華中理工大學出版社,1997
P207
B
1672-4623(2016)08-0064-03
10.3969/j.issn.1672-4623.2016.08.021
潘軼,碩士研究生,研究方向為精密工程測量。
2015-11-09。
項目來源:國家自然科學基金資助項目(41174002)。

