軟可補子半環

袁惠淑，袁志玲，孔祥智

(江南大學理學院，江蘇 無錫 213122)

軟可補子半環

袁惠淑，袁志玲，孔祥智

(江南大學理學院，江蘇 無錫 213122)

定義了軟可補子半環的概念，研究了軟可補子半環的基本性質.進一步，應用對偶軟集的方法研究了軟可補子半環和對偶軟集之間的關系.最后，探討了軟可補子半環像與原像的性質.

軟集；對偶軟集；可補子半環；軟可補子半環

Zadeh[1]提出的模糊集理論、Pawlak[2]提出的粗糙集理論與Atanassov[3]提出的直覺模糊集理論都是刻畫不完整性和不確定性信息的數學工具.但這些數學理論都存在參數工具不足的缺陷，針對此問題，Molodstov[4]提出了軟集的概念，它是一個包含模糊集、直覺模糊集、粗糙集等內涵的理論，許多學者在這方面做出大量工作.

目前，軟集理論被廣泛應用到數學、信息科學、計算機科學等各個領域.將軟集與代數學交叉，Aktas和Cagman[5]提出了軟群的新概念，并討論了其基本性質，建立了軟代數學的新研究領域.楊聞起[6]提出交換可剩余半群的剩余BCI-代數的概念，討論其性質并給出了軟半群的剩余BCI-代數，使半群的理論進一步得到充實.Ummahan等[7]把軟集理論運用到環中，建立了軟環理論.廖祖華等[8]在軟集理論的基礎上給出了軟坡的概念，并進一步研究了它的一些相關性質.

半環是環概念的推廣，將軟集運用到半環上，得到了很多有價值的結果.豐建文等[9]提出了可補半環的概念.本文將軟集理論運用到可補半環上，提出了軟可補子半環的概念，并研究了它的一些基本性質.

1 預備知識

設U是初始全集，E是參數集，P(U)表示U的冪集，A?U.

定義1.1[10]設F：A→P(U)為映射，則稱(F，A)為集合U上的軟集.

定義1.2[8](軟集的交) 設(F，A)，(G，B)是U上的軟集.若軟集(H，C)滿足：

(1)C=A∩B；

(2)?e∈C，H(e)=F(e)∩G(e).

則稱(H，C)是軟集(F，A)和(G，B)的交，記作(H，C)=(F，A)∩(G，B).

定義1.3[10](軟集的且運算) 設(F，A)，(G，B)是U上的軟集，令(H，A×B)=(F，A)∧(G，B)，其中H(α，β)=F(α)∩G(β)，?(α，β)∈A×B.則稱(H，A×B)是(F，A)與(G，B)的且運算，記為(F，A)∧(G，B).

為軟集H的對偶.若A：X→P(E)為一個軟集，則軟集

是A對偶.

定義1.5[12]設E是一個具有二元運算“+”和“·”的非空集合，且滿足條件：

(1) (E，+，0)和(E，·，1)都是幺半群；

(2) (E，+)是交換半群；

(3) ?a，b，c∈E，(a+b)c=ac+bc和c(a+b)=ca+cb；

(4) ?a∈E，0·a=a·0=0.

則稱E為結合半環，簡稱半環.若E只滿足條件(1)，(3)，(4)，則稱E為加法非交換半環.

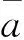
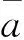
定理1.2[13]E是可補半環，則E是乘法冪等的，即aa=a，?a∈E.

定理1.3[13]可補半環E必是加法和乘法可交換的.

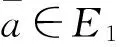
定義1.8[7](同態映射) 設E1，E2是可補半環，f：E1→E2為一個映射.稱f是同態映射，若滿足：

(1)f(a+b)=f(a)+f(b)，?a，b∈E1；

(2)f(ab)=f(a)f(b)，?a，b∈E1；

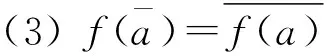
定義1.9[7](笛卡爾積)A，B是兩個非空集合，記A×B為A，B的笛卡爾積，且

A×B={(x，y)|x∈A，y∈B}.

定義1.10[7](笛卡爾積的乘法運算)A，B是兩個非空集合，定義A×B上的乘法運算，使得?(x，y)，(m，n)∈A×B，(x，y)(m，n)=(xm，yn).

定義1.11[7]設E1，E2是可補半環，規定E1×E2的運算為：

(1) (x1，y1)+(x2，y2)=(x1+y1，x2+y2)，?x1，x2∈E1，y1，y2∈E2；

(2) (x1，y1)·(x2，y2)=(x1y1，x2y2)，?x1，x2∈E1，y1，y2∈E2；

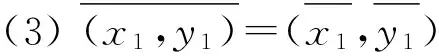
定理1.4 設E1，E2是可補半環，則E1×E2是可補半環.

證明 易證E1×E2滿足加法交換律、加法結合律、乘法結合律、乘法對加法的左右分配律.?(x1，y1)∈E1×E2，有

(x1，y1)+(0，0)=(x1+0，y1+0)=(x1，y1)=(0+x1，0+y1)=(0，0)+(x1，y1)，

故(0，0)是加法單位元；又因為

(x1，y1)(1，1)=(x11，y11)=(x1，y1)=(1x1，1y1)=(1，1)(x1，y1)，

故(1，1)是乘法單位元；由

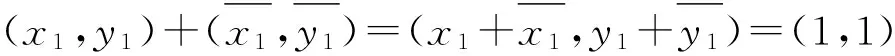
且

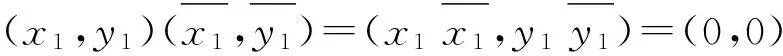
定理1.5[13]設E1，E2是可補半環E的可補子半環.若E1∩E2≠?，則E1∩E2也是E的可補子半環.

由定義1.8的條件(3)，有如下結論.

2 軟可補子半環

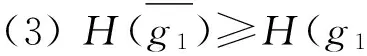
定理2.1 設E是可補半環，H：E→P(X)為一個軟集.若H為E的軟可補子半環，則

H(g1g2)?H(g1)∩H(g2)，?g1，g2∈E，

證明 因為H是E的軟可補子半環，?g1，g2∈E，有

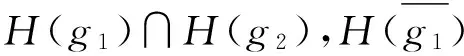
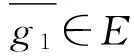
定理2.2 設E1，E2分別是可補半環E的可補子半環，H1，H2分別為E1，E2的軟可補子半環.若E1∩E2≠?，(H，E1∩E2)=(H1，E1)∩(H2，E2)，則H是E1∩E2的軟可補子半環.

證明E1，E2是可補半環E的可補子半環，且E1∩E2≠?，由定理1.5知E1∩E2也是E的可補子半環.?g1，g2∈E1∩E2，

H(g1+g2)=H1(g1+g2)∩H2(g1+g2)?[H1(g1)∩H1(g2)]∩[H2(g1)∩H2(g2)]=

[H1(g1)∩H2(g1)]∩[H1(g2)∩H2(g2)]=H(g1)∩H(g2)，

H(g1g2)=H1(g1g2)∩H2(g1g2)?[H1(g1)∩H1(g2)]∩[H2(g1)∩H2(g2)]=

[H1(g1)∩H2(g1)]∩[H1(g2)∩H2(g2)]=H(g1)∩H(g2)，

從而H是E1∩E2的軟可補子半環.

定理2.3 設E1，E2分別是可補半環，H1，H2分別是E1，E2的軟可補子半環.令E=E1×E2，則軟集(H，E)=(H1，E1)∧(H2，E2)是E的軟可補子半環.

證明 因為E1，E2是可補半環，由定理1.4知E1×E2也是可補半環.?(x，y)，(m，n)∈E，有：

H[(x，y)+(m，n)]=H(x+m，y+n)=H1(x+m)∩H2(y+n)?[H1(x)∩H1(m)]∩

[H2(y)∩H2(n)]=[H1(x)∩H2(y)]∩[H1(m)∩H2(n)]=H(x，y)∩H(m，n)，

H[(x，y)(m，n)]=H(xm，yn)=H1(xm)∩H2(yn)?[H1(x)∩H1(m)]∩[H2(y)∩

H2(n)]=[H1(x)∩H2(y)]∩[H1(m)∩H2(n)]=H(x，y)∩H(m，n)，

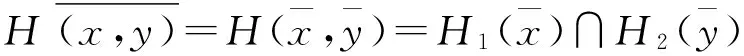
從而可知(H1，E1)∧(H2，E2)是E1×E2的軟可補子半環.

定理2.4 (1)H是E的軟可補子半環，當且僅當AH(x)是E的可補子半環，?x∈X；

(2) 設A：X→P(E).則?x∈X，A(x)是E的可補子半環，當且僅當HA是E的軟可補子半環.

證明 (1) 必要性.?g1，g2∈AH(x)，則x∈H(g1)且x∈H(g2)，所以x∈H(g1)∩H(g2).因為H是E的軟可補子半環，

H(g1)∩H(g2)?H(g1+g2)，H(g1)∩H(g2)?H(g1g2)，

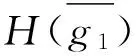
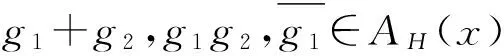
H(g1)∩H(g2)?H(g1+g2)；

H(g1)∩H(g2)?H(g1g2)；

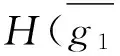
所以H是E的軟可補子半環.

(2) 必要性.一方面，?x∈HA(g1)∩HA(g2)，g1∈A(x)，g2∈A(x).又因為A(x)是E的可補子半環，g1+g2∈A(x)，即x∈HA(g1+g2).故：

HA(g1)∩HA(g2)?HA(g1+g2)；

g1g2∈A(x).

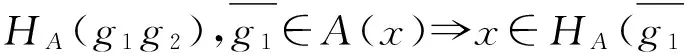
綜上，HA是E的可補子半環.

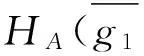
綜上，由定義1.7知A(x)是E的軟可補子半環.

3 軟可補子半環的像與原像

定義3.1[7]設E1，E2是可補半環，X是初始集合.f：E1→E2是一個映射，H1：E1→P(X)和H2：E2→P(X)是軟集.定義

f-1(H2)(g1)=H2(f(g1)).

則f(H1)，f-1(H2)分別為E2，E1上的軟集，稱f(H1)為H1的像，f-1(H2)為H2的原像.

定理3.1 設E1，E2是可補半環，X是初始集合，f：E1→E2是一個同態映射，H1：E1→P(X)與H2：E2→P(X)為軟集.則：

(1) 若H1為E1的軟可補子半環，則f(H1)為E2的軟可補子半環；

(2) 若H2為E2的軟可補子半環，則f-1(H2)為E1的軟可補子半環.

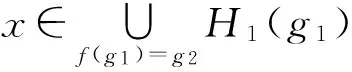
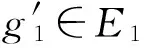
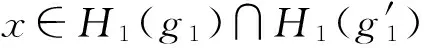
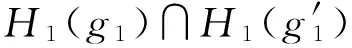
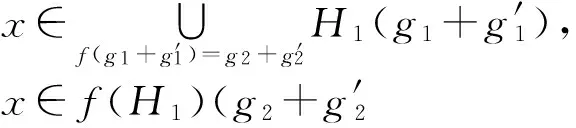
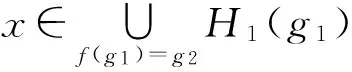
綜上，f(H1)是E2的軟可補子半環.

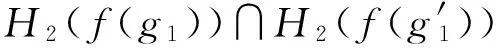
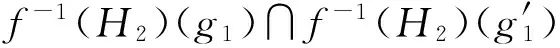
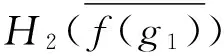
綜上，f-1(H2)是E1的軟可補子半環.

[1] ZADEH L A.Fuzzy sets[J].Information and Control，1965，8：338-353.

[2] PAWLAK Z.Rough sets[J].International Journal of Information Computer Science，1982，11：341-356.

[3] ASTANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20：87-96.

[4] MOLODTSOV D.Soft set theory：first results[J].Computers and Mathematics with Applications，1999，37：19-32.

[5] AKTAS H，CAGMAN N.Soft sets and soft groups[J].Information science，2007，177：2726-2735.

[6] 楊聞起.交換可剩余半群的剩余BCI-代數[J].東北師大學報(自然科學版)，2015，47：22-25.

[7] UMMAHAN ACAR，FATIH KOYUNCU，BEKIR TANAY.Soft sets and soft rings[J].Computers and Mathematics with Applications，2010，11：3458-3463.

[8] 廖祖華，芮明力.軟坡[J].計算機工程應用，2012(2)：30-32.

[9] 豐建文，黃福生，石定琴.可補半環[J].江西科學，2005，23(3)：207-209.

[10] MAJI P K，ROY A R.Soft set theory[J].Computers Mathematics with Applications，2003，45：555-562.

[11] 溫永川.關于軟集的研究[D].遼寧：遼寧師范大學，2008.

[12] 蒲保明，劉應明.不分明拓撲學Ⅰ：不分明點的鄰近構造與Moore-Smith式收斂[J].四川大學學報(自然科學版)，1977(1)：31-50.

[13] 豐建文，詹棠森.可補半環上的同余[J].模糊系統與數學，2010，24(6)：61-65.

(責任編輯：李亞軍)

Soft complemented subsemiring

YUAN Hui-shu，YUAN Zhi-ling，KONG Xiang-zhi

(School of Science，Jiangnan University，Wuxi 213122，China)

The concept of soft complemented subsemiring is given and some basic properties of soft complemented subsemiring are obtained.Furthermore，by adopting the dual soft sets，some properties of soft complemented subsemirings and the links with its dual soft sets are founded.Finally，the image of soft complemented subsemiring is discussed，also as the preimages.

soft sets；dual soft sets；complemented subsemiring；soft complemented subsemiring

1000-1832(2016)04-0005-05

10.16163/j.cnki.22-1123/n.2016.04.002

2015-06-14

國家自然科學基金資助項目(11371174，11301227)；江蘇省自然科學基金資助項目(BK20130119).

袁惠淑(1986—)，女，碩士，主要從事模糊代數研究；袁志玲(1974—)，女，碩士，副教授，主要從事模糊代數研究；孔祥智(1971—)，男，博士，教授，主要從事模糊代數研究.

O 153 [學科代碼] 110·44

A