光滑映射芽的RL-有限決定性

董艷青，何瑞瑞，劉恒興

(武漢大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖北 武漢 430072)

光滑映射芽的RL-有限決定性

董艷青，何瑞瑞，劉恒興

(武漢大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖北 武漢 430072)

為研究實(shí)空間上光滑映射芽RL-等價關(guān)系下的相關(guān)問題，需要討論光滑映射芽的RL有限決定性.討論及計(jì)算了光滑映射芽在群RL-作用下的軌道切空間，得到了光滑映射芽的RL-有限決定的充分必要條件.

光滑映射芽；RL-有限決定；RL-等價關(guān)系；切空間；向量場

0 引言

映射芽的有限決定性問題是奇點(diǎn)理論中的一個基本問題.若ε0(n，p)表示從(Rn，0)到(Rp，0)的全體光滑映射芽構(gòu)成的環(huán)，對于一個給定的等價關(guān)系E，稱f∈ε0(n，p)是r-E-決定的，意指對任意的g∈ε0(n，p)，如果g與f有相同的r階Taylor多項(xiàng)式，那么f是E-等價于g的.Mather[1]討論了光滑映射芽f：(Rn，0)→(Rp，0)在群L，R，C，A和K作用下的有限決定性問題，并給出了它們的有限決定的充要條件.

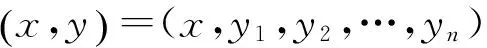
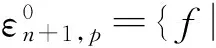
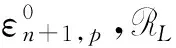
1 光滑映射芽在群RL作用下的軌道切空間

光滑函數(shù)芽f的“切空間J(f)”為研究光滑函數(shù)芽的R-決定性提供了重要信息.因此，有必要對映射芽f∈Mn+1×(Mn+1g)p-1的軌道RL·f在f處的切空間予以討論.

首先考慮f0∈Mn+1×(Mn+1g)p-1的切空間.

(1)

F°Φ=1(R，0)×f0.

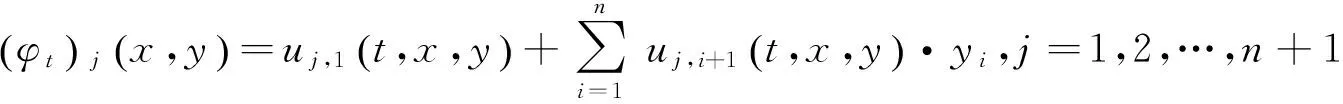
(2)

(3)

(4)

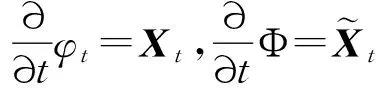
又

其中Dft表示ft關(guān)于點(diǎn)(x，y)處的Jacobian矩陣.則(4)式可表示為

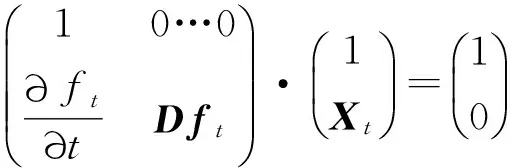
即

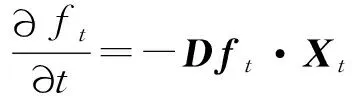
(5)

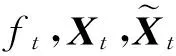
若記

定義1.2 設(shè)f∈Mn+1×(Mn+1g)p-1，軌道RL·f在f處的切空間TRL(f)定義為

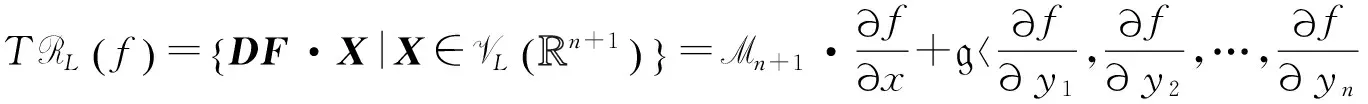
引理1.1[5]設(shè)G是代數(shù)作用在一個光滑代數(shù)簇M上的代數(shù)群，則對應(yīng)的軌道是M中的光滑擬代數(shù)子集.

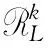
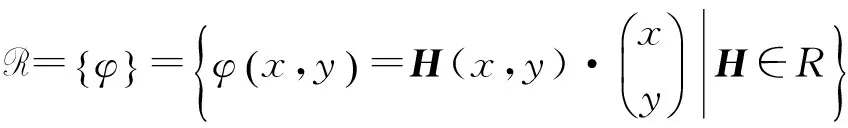
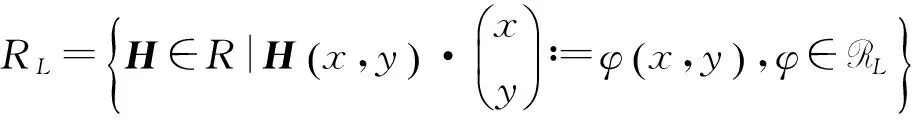
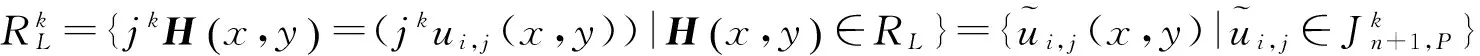
定義1.3

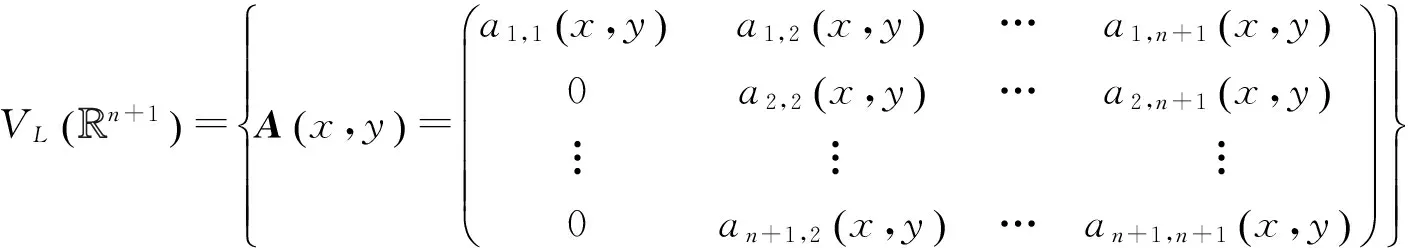
記：

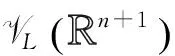
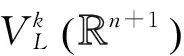
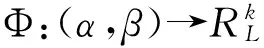
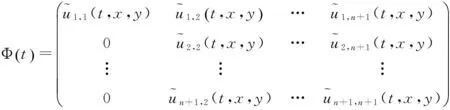
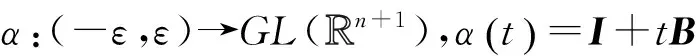
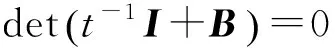
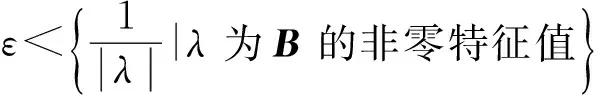
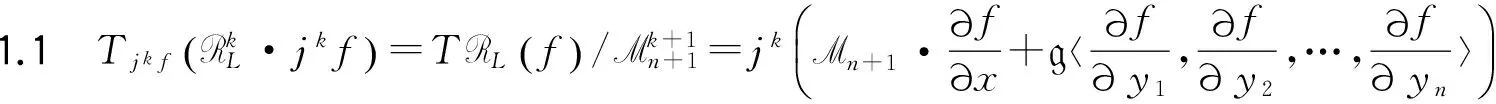
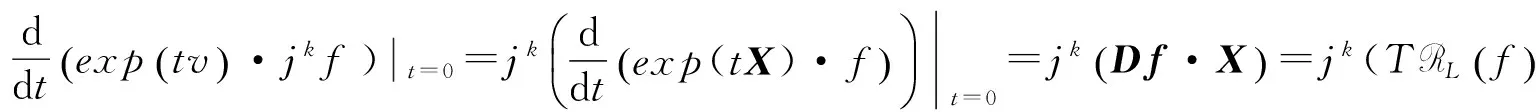
故

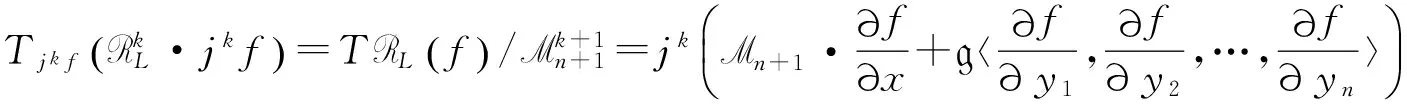
命題1.1蘊(yùn)含了定義1.2是合理的.

2 光滑映射芽的RL-有限決定性

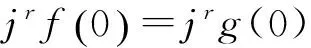
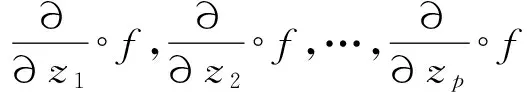
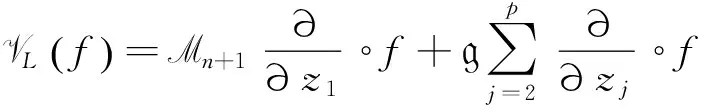
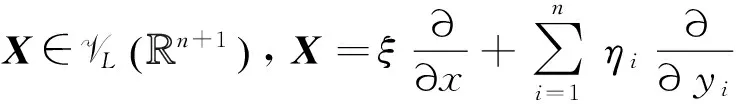
定理2.1 設(shè)f∈Mn+1×(Mn+1g)p-1.

為證明定理2.1，需要下面一些結(jié)論.

引理2.1 設(shè)f，g∈Mn+1×(Mn+1g)p-1，且具有相同的l-導(dǎo)網(wǎng)，則

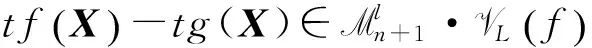
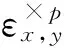
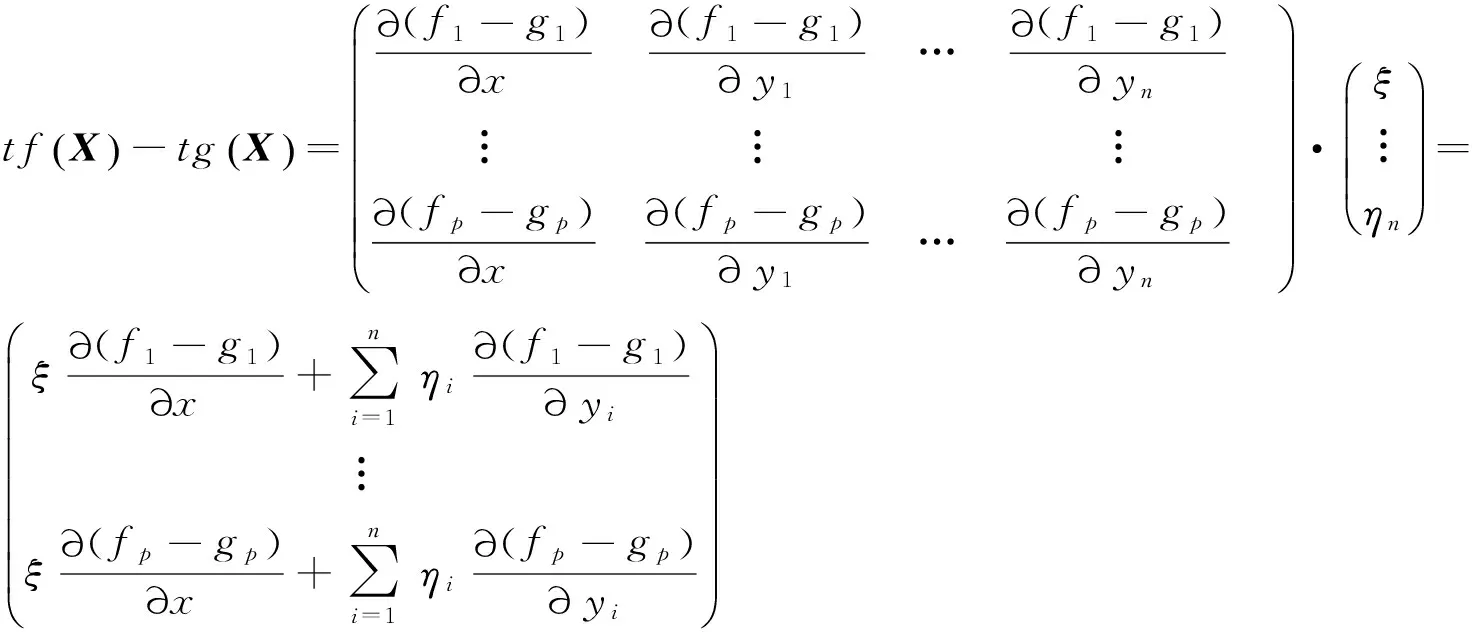
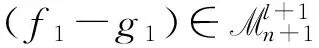
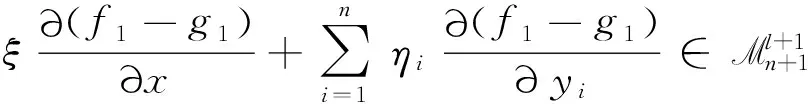
由引理2.1，易得下面結(jié)論.

對單參數(shù)族映射芽，有類似的逼近引理.

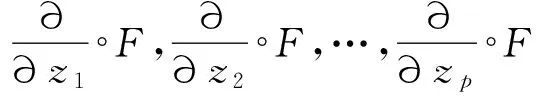
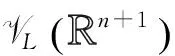
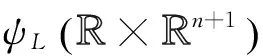
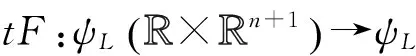
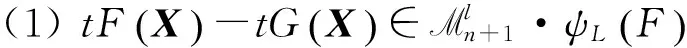
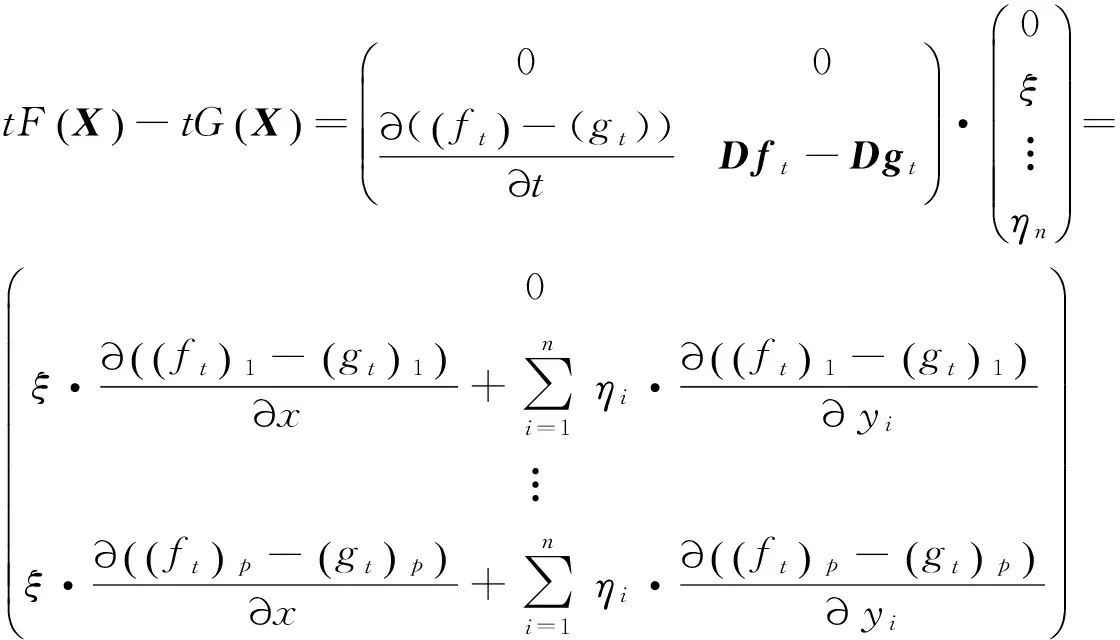
又由于

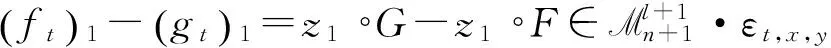
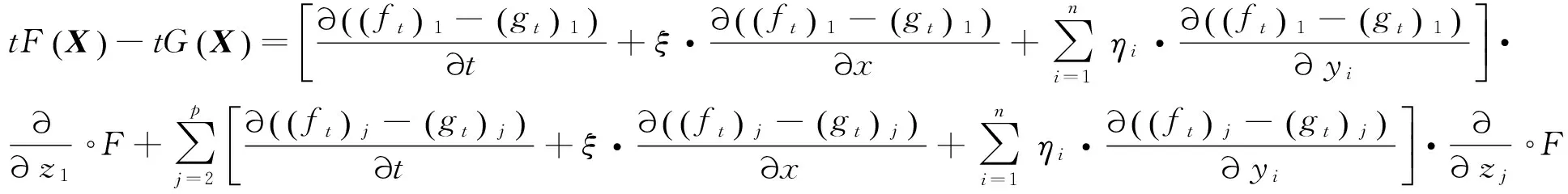
(2)的證明類似于引理2.2的證明.

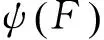
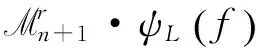
證明 其證明過程和文獻(xiàn)[4]中引理10.2.5的證明過程類似，此處略去.

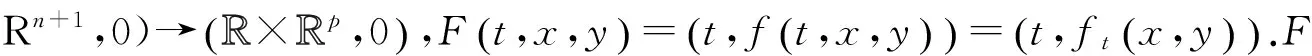
證明 因

使得

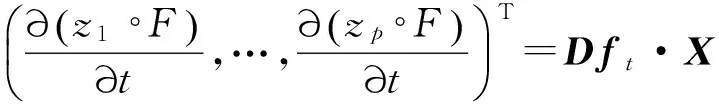
(6)

(7)

(7)式對應(yīng)的微分方程為

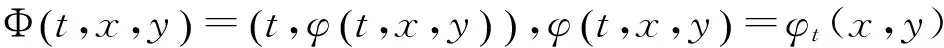
在證明定理2.1之前，我們先給出由文獻(xiàn)[4]定義的一個映射

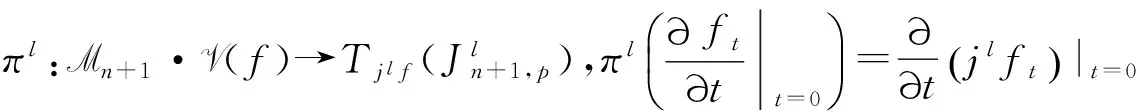
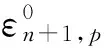
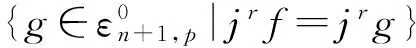
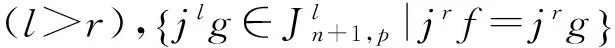
Tjlf{jlg∈Jln+1，p|jrf=jrg}?Tjlf{jlg∈Jln+1，p|f～RLg}.

由文獻(xiàn)[4]可知

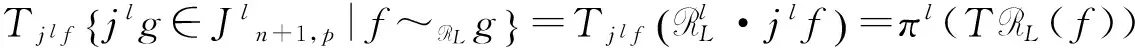
取l=r+1，由Nakayama引理有

故結(jié)論(1)成立.

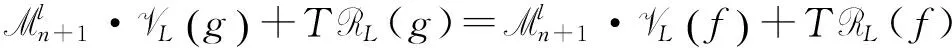
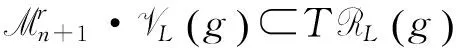
(8)

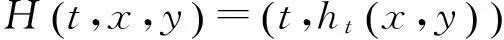
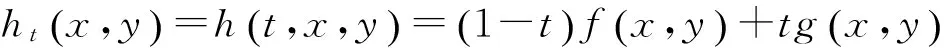
令F=1(R，0)×ha，其中1(R，0)是R上的恒同映射芽.根據(jù)引理2.4，

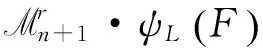
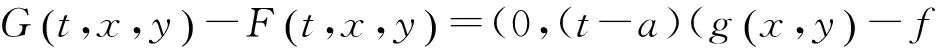
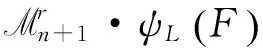
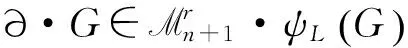
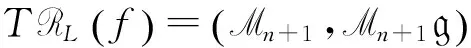
則f是RL-有限決定的.

類似計(jì)算得

從而f是R-有限決定的.

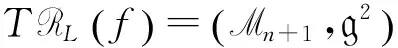
則f不是RL-有限決定的.

同樣可以算得

從而f是R-有限決定的.

上面的兩個例子說明，RL是更細(xì)于R的一個關(guān)系，因此可以利用群RL對Mn+1×(Mn+1g)p-1?ε0(n，p)中的映射芽來進(jìn)行分類.

[1] MATHER J.Stability ofC∞mappings Ⅲ：finitely determined map-germ[J].Pulb Math IHES，1969，35：127-156.

[2] SIERSMA D，JIANG G F.Local embeddings of lines in singular hypersurfaces[J].Ann Inst Fourier，1999，49(4)：1129-1147.

[3] SIERSMA D.Isolated line singularities[J].Proc Sympos Pure Math，1983，40：485-496.

[4] 李養(yǎng)成.光滑映射的奇點(diǎn)理論[M].北京：科學(xué)出版社，2002：159-182，207-220.

[5] DIMCA A.Topics on real and complex singularities[M].Braunschweing：Fried Vieweg and Sohn，1987：30-42.

(責(zé)任編輯：李亞軍)

Finite determinacy of smooth map germs under group RL

DONG Yan-qing，HE Rui-rui，LIU Heng-xing

(Department of Mathematics and Statistics，Wuhan University，Wuhan 430072，China)

In order to explore the relevant problems of smooth map germs under RL-equivalence，it is vital to discuss the RL-finite determinacy of smooth map germs.In this paper，the tangent space to orbit of smooth map germs under group =RLis calculated，and a necessary and sufficient condition with respect to RL-finite determinacy of smooth map germs is given.

smooth map germs；finite RL-determinacy；RL-equivalence；tangent space；vector field

1000-1832(2016)04-0027-09

10.16163/j.cnki.22-1123/n.2016.04.007

2015-06-28

國家自然科學(xué)基金青年項(xiàng)目(11501103)；國家自然科學(xué)基金資助項(xiàng)目(11201346).

董艷青(1990—)，女，碩士，助教，主要從事奇點(diǎn)理論研究；何瑞瑞(1990—)，女，碩士，主要從事奇點(diǎn)理論研究；劉恒興(1961—)，男，副教授，主要從事奇點(diǎn)理論研究.

O 192 [學(xué)科代碼] 110·3155

A