柔性二級倒立擺的準滑動模態控制研究
王 玨,謝慕君,李元春
(長春工業大學電氣與電子工程學院,吉林 長春 130012)
柔性二級倒立擺的準滑動模態控制研究
王 玨,謝慕君,李元春
(長春工業大學電氣與電子工程學院,吉林 長春 130012)
柔性二級倒立擺是一個高階非線性強耦合的自然不穩定系統,為了對其進行穩擺控制,基于建模機理建立了柔性二級倒立擺數學模型,提出準滑動模態控制方法,設計了滑模變結構控制器,使系統具有較好的穩擺控制和魯棒性.仿真結果表明:基于準滑動模態控制的滑模變結構控制方法能夠更好地實現倒立擺穩定控制;比傳統指數趨近率的滑模控制器輸出更加平滑,削弱了抖振.
柔性二級倒立擺;滑模變結構;準滑動模態
0 引言
倒立擺系統具有非線性、強耦合、多變量等不穩定特性,從理論上涉及跟蹤、非線性、魯棒性、鎮定等控制系統研究的關鍵問題,因此成為檢驗各種新的控制理論和方法的典型模型.柔性二級倒立擺系統是在直線二級倒立擺系統的基礎上加入了自由彈簧系統,由于閉環系統受彈簧振蕩頻率的限制,對該系統進行穩擺控制變得更加復雜和困難.目前,針對柔性二級倒立擺穩擺控制主要有以下幾種方法:LQR控制方法實現了柔性二級倒立擺的穩擺控制[1],但擺桿存在抖動;傳統滑模變結構控制方法實現了柔性二級倒立擺的穩擺控制[2],但系統輸入存在抖振,魯棒性較差;基于BP神經網絡的模糊控制方法實現了柔性二級倒立擺的穩擺控制[3],但調節時間較長.上述控制方法均實現了柔性二級倒立擺的穩擺控制,但均存在不足.本文針對柔性二級倒立擺的穩擺控制,采用準滑動模態控制思想設計控制器,調節時間較短,降低控制器輸出的抖動程度,提高柔性二級倒立擺系統的魯棒性.
1 柔性二級倒立擺系統模型的建立
彈簧等不確定性因素的存在,使得柔性二級倒立擺的數學模型建立比較困難[4].但在忽略了摩擦、空氣阻力后,可以把其抽象成由勻質擺桿、小車和彈簧組成的系統[5].本文采用機理建模法建立柔性二級倒立擺系統的數學模型,系統參數取自固高科技有限公司柔性倒立擺實驗裝置GLIP2013.該系統抽象的物理模型見圖1.

圖1 柔性二級倒立擺抽象物理模型

對一級擺桿水平方向的受力進行分析可得
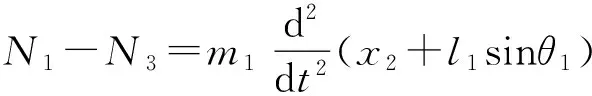
(1)
對一級擺桿垂直方向的受力進行分析可得

(2)
一級擺桿力矩平衡方程為

(3)
對質量塊水平方向的受力進行分析可得

(4)
對質量塊垂直方向的受力進行分析可得

(5)
對二級擺桿水平方向的受力進行分析可得

(6)
對二級擺桿垂直方向的受力進行分析可得

(7)
二級擺桿力矩平衡方程為

(8)
其中

設θ1=π+φ1,θ2=π+φ2(φ1與φ2分別是一級擺桿、二級擺桿與垂直向上方向的夾角),并假設
φ1?1 rad,φ2?1 rad.
(9)

(10)
代入參數后得:
(11)

(12)
將從動小車、擺桿和質量塊看做一個整體進行受力分析,可得

(13)
令

則傳遞函數轉化為


(14)
則系統的狀態空間方程為

(15)
其中:




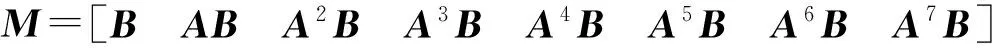
由系統的狀態空間方程可看出,柔性二級倒立擺系統是強耦合、高階不穩定系統.針對該復雜系統的穩擺控制,設計如下控制器,使其不僅達到較好的穩擺控制效果且控制器輸出抖動較小.
2 準滑動模態控制器的設計
在實際工程中,由于存在時間的延遲和空間上的滯后使得在滑模控制系統中滑動模態呈抖振形式[6].因此,本文采用準滑動模態控制系統.
所謂準滑動模態是指系統的運動軌跡被限制在理想滑動模態的某一Δ鄰域內的模態.從相軌跡方面來說,就是使一定范圍內的運動狀態點均吸引至切換面的某一Δ鄰域內,通常稱該Δ鄰域為滑動模態切換面的邊界層[7].在邊界層內,準滑動模態是不要求滿足滑動模態的存在條件的.
該控制器設計的基本步驟包括切換函數s(x) 的設計和準滑動模態控制率u(x)的設計2個相對獨立的部分.
2.1 切換函數的設計
切換函數[8]為
s=Zx.
(16)
采用Ackermann公式設計Z值為
Z=eTP(λ).
(17)
Ackermann公式為:
eT=[0,…,0,1][b,Ab,…,An-1b]-1;
(18)
P(λ)=(λ-λ1)(λ-λ2)…(λ-λn-1).
(19)
在二級柔性倒立擺系統中,當n=8,取λ1=-5,λ2,3=-50±0.7i,λ4,5=-25±2.7i,λ6,7=-35±2.7i,根據Ackermann公式設計Z值,可得Z=[225,1,-188.28,13.47,-4.61,-2.23,-32.15,-5.94].
2.2 準滑動模態控制率的設計
準滑動模態控制率為
(20)
其中
(20)式中Δ稱為邊界層.該控制率的實質是在邊界層外,采用基于指數趨近率的切換控制,在邊界層之內,采用線性反饋控制[9].

(21)
把(20)式帶入(21)式得系統控制率
u=(ZB)-1(-ZAx-εs2sat(s)-ks).
(22)
3 仿真分析

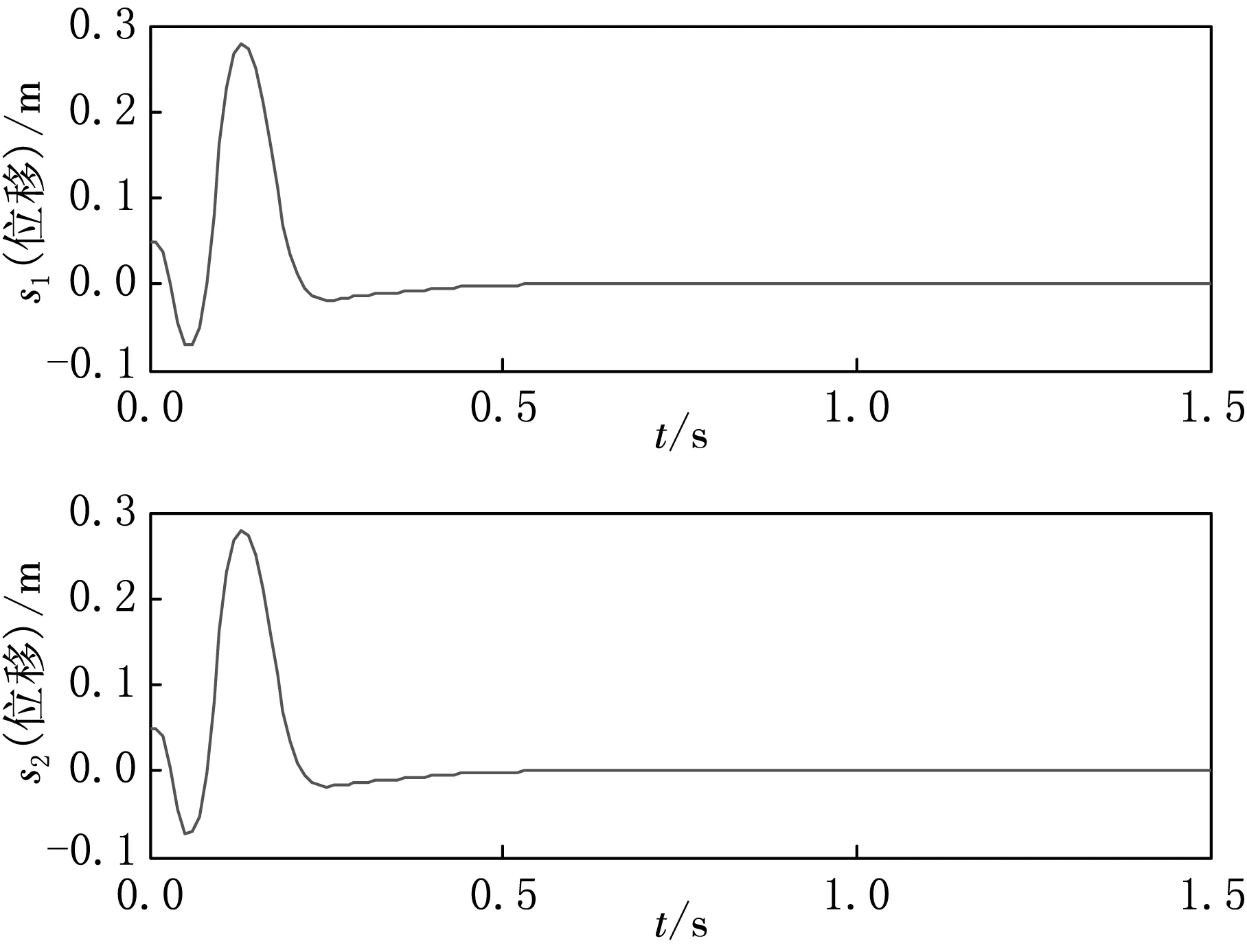
圖2 傳統指數趨近率滑模控制主、從動小車的位移

圖3 傳統指數趨近率滑模控制一級擺桿、二級擺桿的角度

圖4 傳統指數趨近率滑模控制控制器的輸出
從圖2和3可以看出,基于傳統指數趨近率的柔性二級倒立擺滑模控制位置跟蹤速度比較快,圖4的控制器的輸出具有較強的抖振,因此增加了控制器的負擔.

圖5 準滑動模態控制主、從動小車的位移

圖6 準滑動模態控制一級擺桿、二級擺桿的角度

圖7 準滑動模態控制控制器的輸出
從圖5和6可以看出,準滑動模態控制的柔性二級倒立擺保證了位置跟蹤速度,圖7的控制器輸出趨于平滑,因此有效地減弱了柔性二級倒立擺系統的抖動.由于基于傳統指數趨近率的控制使一定范圍內的狀態點被吸引至切換面,準滑動模態控制使一定范圍內的狀態點被吸引至切換面的某一Δ鄰域內,因此,在使用MATLAB進行仿真的過程中,從開始運行到得到仿真結果,準滑動模態控制使用時間在1 s左右,傳統指數趨近率的滑模控制使用時間在10 s左右,提高了運行效率.
4 結束語
本文針對柔性二級倒立擺的穩擺控制,設計了準滑動模態滑模控制器,通過MATLAB仿真實驗驗證了此控制器對于該系統的有效性.從仿真曲線可以看出,系統在0.9 s內迅速達到穩定,相對比基于傳統指數趨近率的滑模控制,準滑動模態滑模控制抑制了控制器的輸出抖動,魯棒性更優.
[1] 吳昊,秦志強,朱學峰,等.直線柔性連接兩級倒立擺控制器設計[J].控制工程,2003,10(6):497-499.
[2] 姜峰.直線二級柔性倒立擺的滑模變結構控制仿真研究[J].科技向導,2013(3):81-82.
[3] YU JIMIN,HUANG LINYAN. Fuzzy control of linear flexible double inverted pendulum sustem [C]// 2012 International Conference on Control Engineering and Communication Technology,Washington:IEEE Computer Society,2012:342-345.
[4] ANIRBAN BANREJEE,NIGAM M J. Designing of proportional sliding mode controller for linear one stage inverted pendulum [J].Power Engineering and Electrical Engineering,2011(9):84-89.
[5] PUNITKUMAR BHAVSAR,VIJAY KUMAR. Trajectory tracking of linear inverted pendulum using integral sliding mode control [J]. Intelligent Systems and Applications,2012(6):31-38.
[6] 劉金琨.滑模變結構控制MATLAB仿真[M].北京:清華大學出版社,2005:32-79.
[7] 高為炳.離散時間系統的變結構控制[J].自動化學報,1995,21(2):154-161.
[8] 謝慕君,王輝.模糊趨近率的滑模控制在倒立擺系統中的應用研究[J].自動化技術與應用,2008,27(10):8-11.
[9] 章仁華,馬靜.航空發動機準滑動模態變結構控制[J].計算機仿真,2011,28(1):103-106.
[10] 劉金琨,孫富春.滑模變結構控制理論及其算法研究與進展[J].控制理論與應用,2007,24(3):407-418.
(責任編輯:石紹慶)
Research on the control of flexible double inverted pendulum system based on quasi-sliding-mode control
WANG Jue,XIE Mu-jun,LI Yuan-chun
(Institute of Electrical and Electronic Engineering,Changchun University of Technology,Changchun 130012,China)
Flexible double inverted pendulum system is a higher order,nonlinear and strong coupling unstable system. In order to steady the pendulum,a mathematical model based on mechanism modeling method is established,and quasi sliding mode control method is put forward,then the sliding mode controller is designed. And then the system has good stability control and robustness. The simulation results show that,the quasi sliding mode control can realize stable control of inverted pendulum,and it is more smooth than general sliding mode control based on exponent trending law in system input,and reducing the shake of the system.
flexible double inverted pendulum system;sliding mode control;quasi sliding mode
1000-1832(2016)04-0083-05
10.16163/j.cnki.22-1123/n.2016.04.018
2015-06-09
國家自然科學基金資助項目(61374051).
王玨(1990—),女,碩士研究生;通訊作者:謝慕君(1969—),女,博士,教授,主要從事智能機械與機器人技術和現代節能技術研究.
TP 273 [學科代碼] 510·80
A

