關于4階極小漸近基的一個結果
李靜文,凌燈榮
(安徽師范大學數學計算機科學學院,安徽 蕪湖 241003)
關于4階極小漸近基的一個結果
李靜文,凌燈榮
(安徽師范大學數學計算機科學學院,安徽 蕪湖 241003)
設h≥2,若h階漸近基A的任一真子集均不是h階漸近基,則稱集合A是自然數集N的h階極小漸近基.為進一步刻畫漸近基與極小漸近基之間的關系,本文綜合運用自然數的b進制表示理論及分類討論的方法,證明了存在一個集合是4階漸近基且其任何子集均不是4階極小漸近基.
極小漸近基;5進制表示
1 引言
令集合N是全體非負整數所組成的集合,A?N.對任意整數h≥2,令
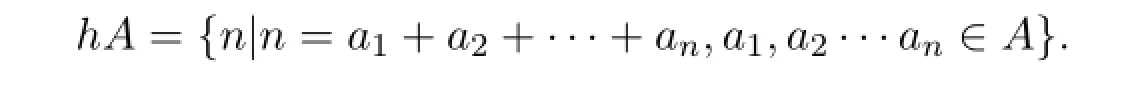
若對任意充分大的整數n均有n∈hA,則稱集合A為h階漸近基.若集合A的任意子集均不是h階漸近基,則稱集合A是h階極小漸近基.對于任意元素a∈A,記Ea=hAh(A{a}),則集合A是h階極小漸近基等價于Ea是無限集.設S?N,若對稱差(S2A)∪(2AS)是有限集,則稱這兩個集合是漸近等價的.若對稱差(S2A)∪(2AS)是無限集,則稱這兩個集合是漸近不等價的.1955年,文獻[1]引入了極小漸近基的概念.1956年,文獻[2]給出了極小基存在的非構造性證明.
1974年,文獻[3]構造了首個極小漸近基且構造了一個2階漸近基滿足任意子集均不是2階極小漸近基.
定理1.1[3]設
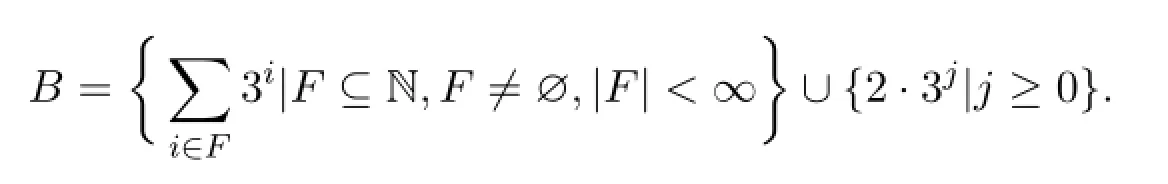
則B是2階漸近基且B不包含任何2階極小漸近基.
1978年,文獻[4]構造了一類有無限多漸近基,但沒有極小漸近基的集合.
定理1.2[4]設p1=2<p2<p3<···是素數序列,m2<m3<···是遞增的正整數序列且滿足對于k≥2有mk+1>2mk+pkpk+3和pkpk-1|mk.設
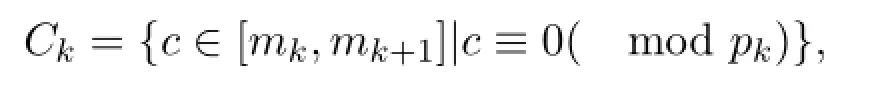
記
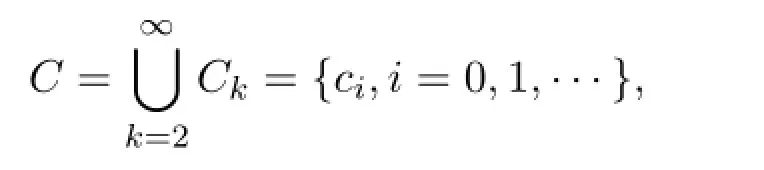
其中c0<c1<c2<···,則C是N的漸近基且滿足
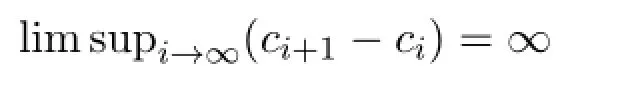
和對于任意有限集F,CF是N的漸近基.
定理1.3[4]存在一類集合S,具有無窮多漸進不等價的漸近基且沒有極小漸近基.
最近凌燈榮和湯敏已構造一個3階漸近基B滿足任意子集均不是3階極小漸近基.本文主要構造了一個4階漸近基B滿足任意子集均不是4階極小漸近基.關于極小漸近基的見相關文獻[5-7].
2 主要結果和證明
定理2.1設
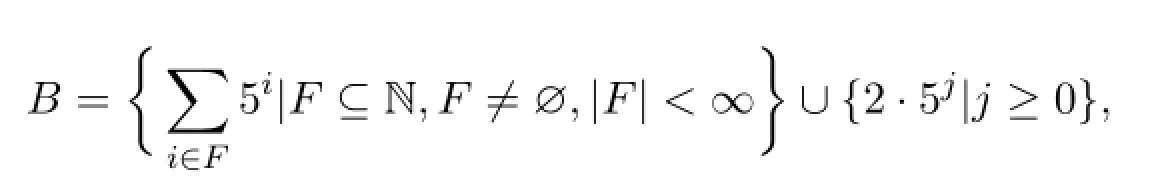
則B是滿足任意子集均不是4階極小漸近基的4階漸近基.


引理2.1若
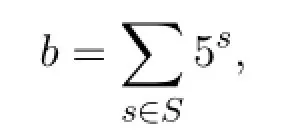
其中S是N的有限子集且card(S)>1,則b是必需的.
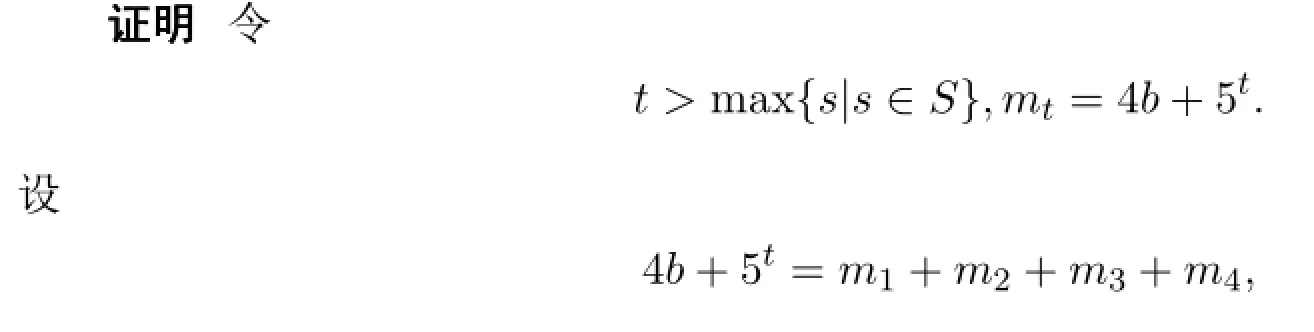

引理2.2若s>0,則5s∈4B的惟一解是5s=5s-1+5s-1+5s-1+2·5s-1.
引理2.3B的任意無限子集是必需的.

引理 2.4B中元素1和B的子集 {5s,2·5s-1},{5s,2·5s},{5s,5s-1}都是必需的,其中s>0.

引理2.5設U和V是N的有限子集,其中
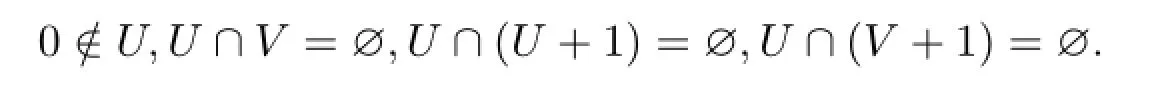








[1]St?hr A.Gel?ste und ungel?ste fragenüber basen der natürlichen zahlenreihe II[J].J.Renie Angew.Math., 1955,194:111-140.
[2]H?rtter E.Ein beitrag zur theorie der minimalbasen[J].J.Renie Angew.Math.,1956,196:170-204.
[3]Nathanson M B.Minimal bases and maximal nonbases in additive number theory[J].J.Number theory, 1974,6:324-333.
[4]Erd?s P,Nathanson M B.Sets of natural numbers with no minimal asymptotic bases[J].Proc.Amer.Math.Soc.,1978,70:100-102.
[5]Jia X D,Nathanson M B.A simple construction of minimal asymptotic bases[J].Acta Arith.,1989,51:95-101.
[6]Lee J B.A construction of minimal asymptotic bases[J].Period.Math.Hungar.,1993,26:211-218.
[7]Ling Deng Rong,Tang Min.On minimal asymptotic g-adic bases[J].Bull.Aust.Math.Soc.,2015,92:374-379.
A note minimal asymptotic basis of order 4
Li Jingwen,Ling Dengrong
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
Let h≥2,an asymptotic basis A of order h is minimal if no proper subset of A is an asymptotic basis of order h.In order to further describe the relationship between asymptotic basis and minimal asymptotic basis,this paper coordinates the theory of the b-adic representation of positive integers and the classification method.We prove that an asypmtotic basis of order 4 containing no subset which is a minimal asymptotic basis of order 4.
minimal asymptotic basis,5-adic representation
O156
A
1008-5513(2016)06-0606-12
10.3969/j.issn.1008-5513.2016.06.006
2016-06-18.
國家自然科學基金(11471017).
李靜文(1992-),碩士生,研究方向:計算數論.
2010 MSC:11B13

