雙差/非差解算模式對定位精度的影響分析

吳 波 ，黨亞民，楊 強，宋傳峰，王丹萍

(1.江蘇省測繪工程院，江蘇 南京 210013；2.中國測繪科學研究院，北京 100830；3.江蘇省蘇測信息科技有限公司，江蘇 南京 21111)

?

雙差/非差解算模式對定位精度的影響分析

吳 波1，黨亞民2，楊 強2，宋傳峰2，王丹萍3

(1.江蘇省測繪工程院，江蘇 南京 210013；2.中國測繪科學研究院，北京 100830；3.江蘇省蘇測信息科技有限公司，江蘇 南京 21111)

針對目前高精度數據處理中雙差網解與非差PPP解2種解算模式間精度差異的問題，進行了相同的觀測數據在上述2種解算模式下的定位精度分析：首先分別闡述了雙差非差數學模型，然后使用地中海周邊若干IGS站觀測數據進行實驗。結果表明：雙差、非差解坐標分量差值在1～2 cm左右；雙差、非差解算模式下，基線較短時基線長度差異較小，最大約為1 cm；隨著基線長度的增加，基線長度差異表現出明顯的累積性；綜合比較坐標分量和基線長度差異可知，雙差解算模式適用于精度要求較高的國家CORS網數據處理，非差處理模式適用于精度相對較低的省級CORS站框架維護。

雙差模式；非差模式；定位精度；基線

0 引言

高頻全球定位系統(global positioning system，GPS)數據處理方法主要有雙差和非差2種模式[1]。數據處理時在載波相位觀測值一次求差的基礎上繼續求差所獲得的虛擬觀測值結果，稱為雙差。雙差觀測消去了衛星鐘差和接收機相對鐘差的影響。此外在站點相距不遠的情況下，雙差可消除大多數電離層和對流層效應[2]。雙差處理模式是目前全球衛星導航系統(global navigation satellite system，GNSS)數據處理中的主流方式。

非差處理模式目前典型的應用是精密單點定位(precise point positioning，PPP)技術。利用國際GNSS服務(international GNSS service，IGS)提供的衛星精密軌道和鐘差產品，外加一臺GPS雙頻接收機即可解算出測站三維坐標、接收機鐘差、衛星鐘差、電離層和對流層延遲改正信息等參數。PPP模式采用單站進行作業，具有定位方式靈活、各測站的解算相互獨立、不受基線長度影響、解算速度快的優點[3]。

已有文獻[4-5]得出網解和非差解等價的結論；但對于對點位精度有嚴格要求的國家基準高精度框架維護，非差解算模式的精度能否達到與雙差解算模式同等精度水平則一直引人關注。本文采用實測數據在雙差和非差模式下進行解算，量化2種解算模式之間解算精度的差異。

1 雙差和非差模型比較

GPS精密定位從觀測值角度可分為非差定位模式和雙差定位模式，本節從誤差源角度給出2種定位模式的具體優勢。

1.1 雙差模型

載波相位雙差數學模型由圖1可得，測站1、2對衛星j、k的載波相位觀測方程[6]為

(1)

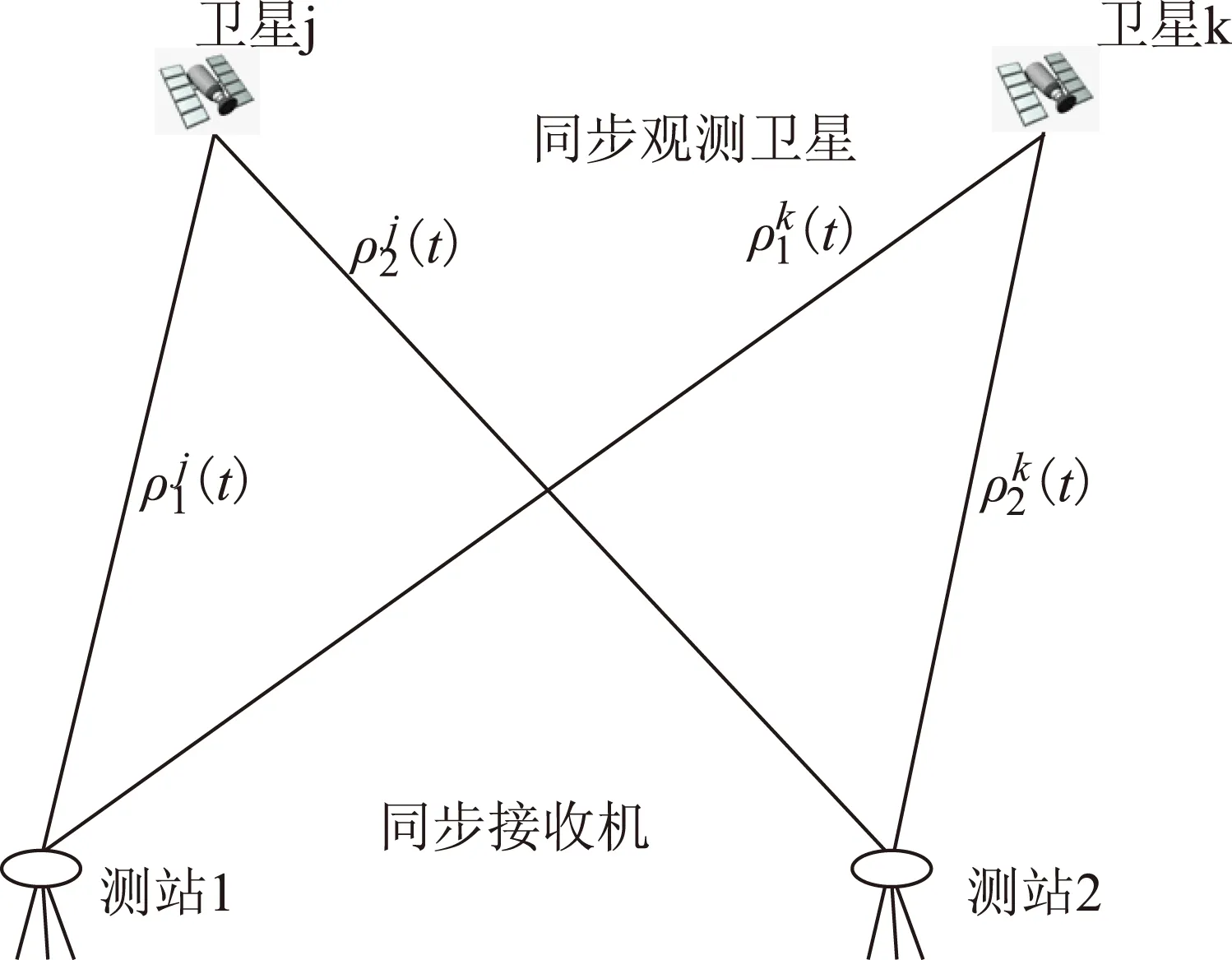
圖1 相對定位圖示

在測站間求單差，再在衛星間求雙差，即可得出雙差觀測方程為

ΔNk。

(2)

式中：

Δφk(t)=Δφk(t)-Δφj(t)；

(3)

ΔNk=ΔNk-ΔNj；

(4)

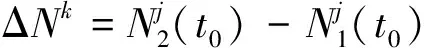
(5)

其中：Δφk(t)表示測站間的載波相位觀測量之差；ΔNk表示2測站觀測同一顆衛星整周模糊度差值。

從雙差觀測方程可以看出：雙差最重要的特點是完全消除了衛星鐘差和接收機鐘差的影響。此外，雙差可消除大多數電離層和對流層效應，特別是測站之間距離不遠的情況[2，7]。

1.2 非差模型

PPP采用雙頻觀測值進行定位時，通常采用無電離層組合觀測值，其基本觀測方程[8-9]為：

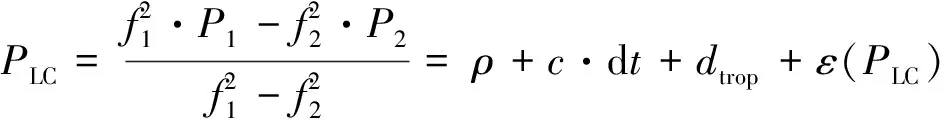
(6)

dtrop+Nλ+ε(ΦLC)。

(7)

式中：Pi為偽距觀測值；Φi為載波相位觀測值；dt為接收機鐘差；dtrop為天定對流層延遲；fi為載波Li頻率；N為無電離層組合模糊度；ε為隨機噪聲和多路徑誤差；ρ為衛星和接收機之間的幾何距離即

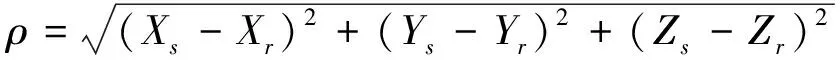
(8)

在精密單點定位中使用非差觀測值，沒有組成差分而是采用精密星歷消除衛星軌道誤差項；利用衛星精密鐘差估計值消去衛星鐘差項；采用雙頻觀載波測值消除了電離層一階項的影響，忽略電離層高階項的影響；采用Hopfield模型、Saastamonien模型，NMF、CMF投影函數進行對流層延遲改正；采用IGS發布的衛星和接收機天線相位中心改正模型進行天線相位中心偏差改正；將接收機鐘差作為一個未知參數進行估計，與其他參數一起解算；通常情況下，非差精密定位數學模型中，多路徑誤差沒有采用模型進行改正，也沒有作為未知數進行估計，因此定位結果中會包含多路徑誤差的影響[7]。

2 雙差網解和非差PPP解的結果比較

為了比較雙差解和非差解實際結果的差異，綜合考慮短(<50 km)、中(50～200 km)、長(>200 km) 3種基線類型，選取地中海沿岸7個IGS站作為待求站，全球均勻選取52個IGS核心站作為公共起算站，站點分布見圖2。公共站的坐標采用強約束，其他站完全放松。待求站數據處理分別采用GAMIT/GLOBK軟件和BERNESE軟件進行：GAMIT軟件是目前非常具有代表性的采用雙差模式的高精度數據處理軟件；BERNESE軟件包含了PPP解功能，對應采用非差解算模式。采用GAMIT軟件進行解算時，解算策略的主要參數設置如表1所示[10]，其他參數采用默認值。PPP的計算利用IGS發布的精密鐘差和最終軌道，連續地處理所有待求IGS站的數據；數據處理的基本設置如同GAMIT軟件，站坐標參數完全放松。從站點坐標分量和基線長2方面對實驗結果進行比較。

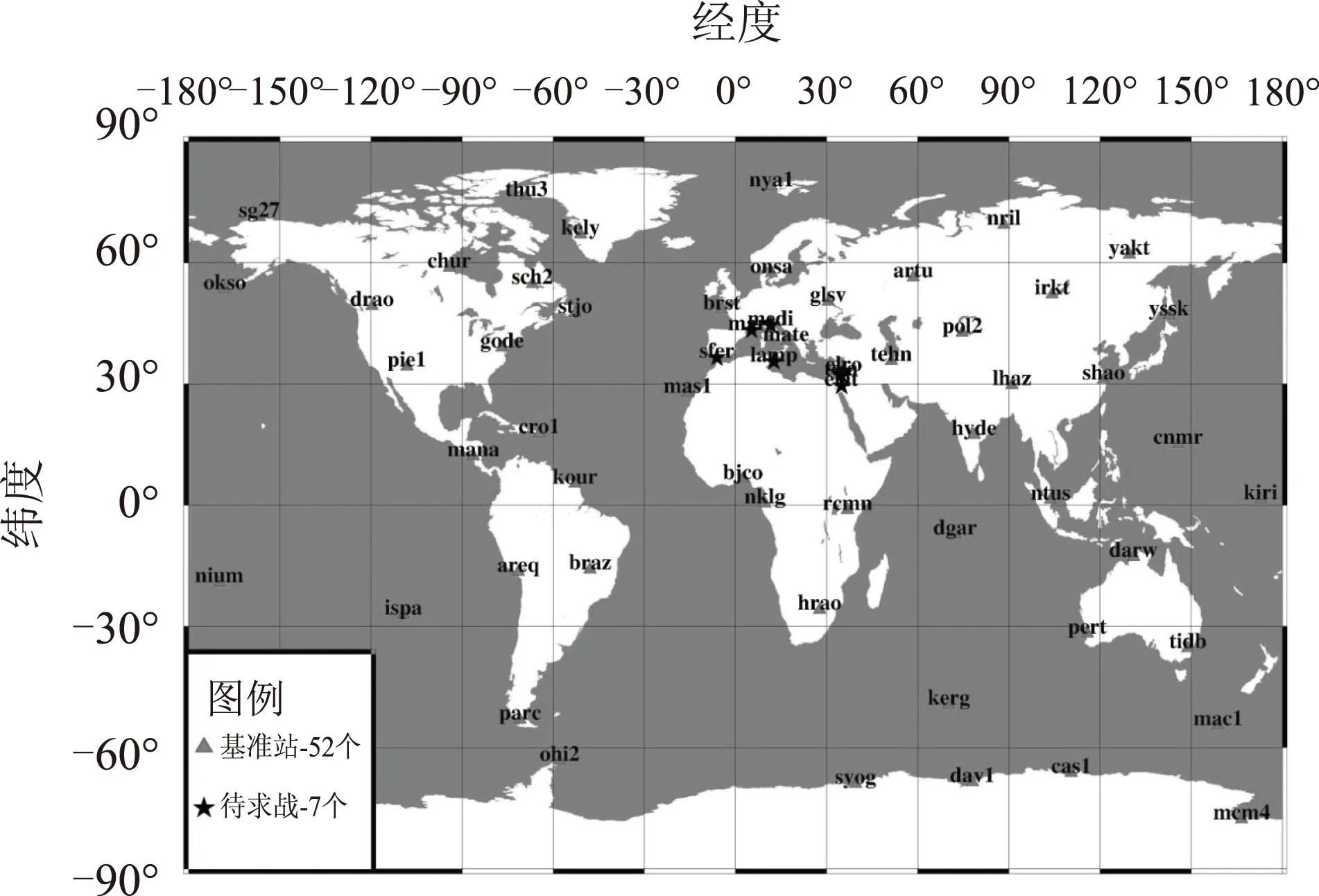
圖2 基準站及待求站分布圖

處理參數設置處理參數設置處理模式RELAX潮汐改正不使用觀測值的選取LC?HELP約束站ARTU等對流層誤差模型SAASTAMONIEN其他100100100光壓模型BERNE固定坐標參考框架ITRF2005數據篩選AUTCLN截止高度角10°大地水準面模型EGM96采樣間隔30s

2.1 站坐標絕對值比較

本文選取了2013年年積日328～334連續7 d的觀測數據，圖3顯示了部分待求站雙差解和非差解的坐標值在X、Y、Z方向的差值。根據坐標分量的殘差量級可以發現，雙差和非差解差異在2 cm以內，在實際數據處理中，不能得出雙差解與非差解完全等價的結論。

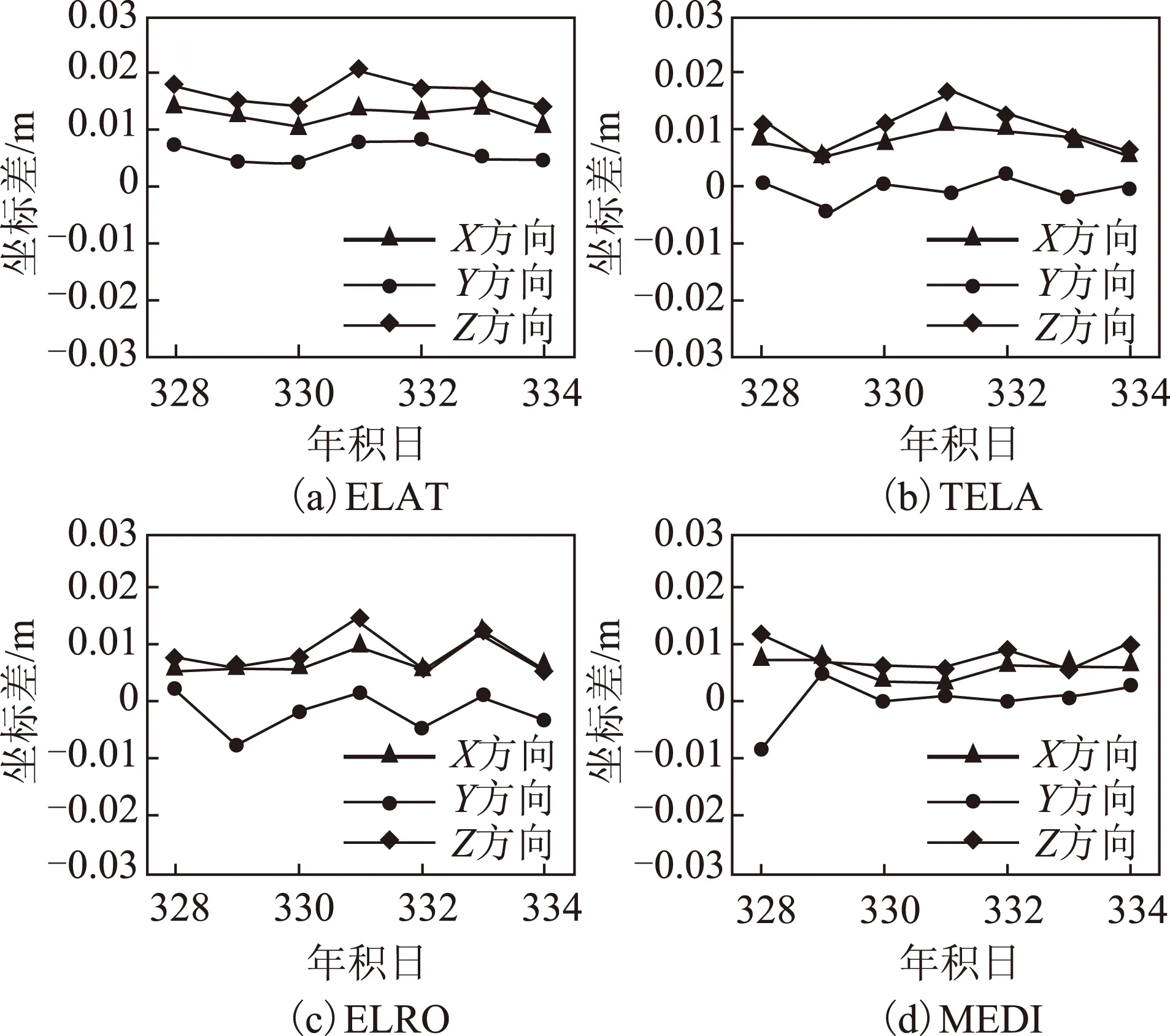
圖3 雙差解和非差解的坐標值比較

2.2 不同模式下基線長度的比較

除坐標外，還比較了2種解算模式下基線長度之間的差異。將經GLOBK平差后站點坐標作為參考值計算所有基線長度，分別與2種解算模式下對應基線長度進行比較，具體差異數值見表2，對應的差值分布如圖4所示。可以發現：非差解算模式下基線長度變化較大；雙差解算模式下基線長度變化較小。當基線較短時，種解算模式下基線長度相差較小，最大約為1 cm。隨著基線長度的增加，2種解算模式下基線長度的差異越發明顯。

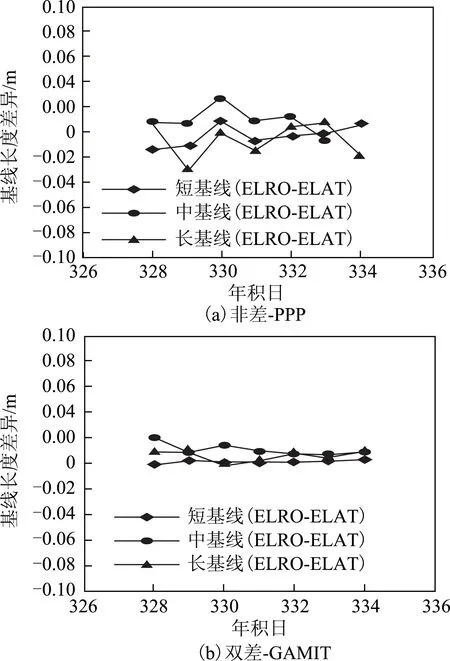
圖4 雙差解和非差解對應不同基線長度比較

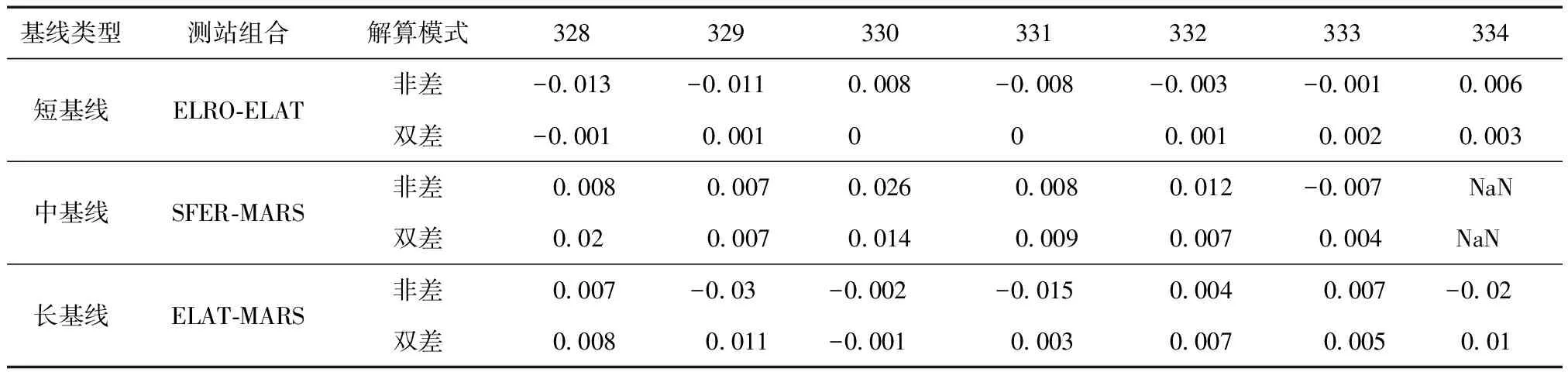
表2 雙差解和非差解對應基線差異數值 m

注：“NaN”表示由于SFER站年積日334 d沒有數據。

3 結束語

雙差解和非差PPP解是當前GPS數據處理中的2種方式。本文通過隨機選取的7個IGS站在2種解算模式下2013年年積日328～334共7 d的坐標分量，經計算、分析得出以下結論：

1)雙差、非差單天解坐標分量的差值在2 cm以內。

2)非差解算模式下計算得出的基線長度變化較大，而雙差解算模式下得出的基線長度變化平穩。

3)基線較短時，雙差、非差解算模式下，基線長度差異較小，最大約為1 cm。

4)隨著基線長度的增加，基線長度的差異表現出明顯的累積性。

對于解算精度要求達到mm級的國家連續運行參考站(continuously operating reference stations，CORS)系統網數據處理，雙差解以其解算精度高的優越性成為其數據處理的主流手段。而對于精度要求在1～2 cm的省級CORS站框架維護，非差解算模式能夠快速完成數據處理，并能夠滿足解算精度，因而成為其數據處理的首選。

[1] 吳繼忠，吳文壇.利用高頻GPS進行地震動態變形分析及地震定位[J].大地測量與地球動力學，2012，32(2)：20-23.

[2] 許國昌.GPS理論、算法與應用[M].李強，劉廣軍，于海亮，等譯.2版.北京：清華大學出版社，2011：151-151.

[3] 黨亞民，秘金鐘，成英燕.全球導航衛星系統原理與應用[M].北京：測繪出版社，2007：78-79.

[4] 劉焱雄，彭琳，周興華，等.網解和PPP解的等價性[J].武漢大學學報·信息科學版，2005，30(8)：736-738.

[5] 韓保民，歐吉坤.基于GPS非差觀測值進行精密單點定位研究[J].武漢大學學報·信息科學版，2003，28(4)：409-412.

[6] 王儷霏，李博峰，張興福.北斗與GPS隨機模型對比分析[J].測繪工程，2014，23(10)：9-13.

[7] 崔陽.大規模測量平差分布式計算技術及應用研究[D].鄭州：信息工程大學，2013： 63-64.

[8] 方榮新，施闖.高采樣率GPS數據非差精密處理方法及其在地震學中的應用研究[D].武漢：武漢大學，2010：30-32.

[9] 辜聲峰.多頻GNSS非差非組合精密數據處理理論及其應用[D].武漢：武漢大學，2013：138-140.

[10]王超，郭際明，周命端，等.高精度GPS數據處理中GAMIT批處理方法與實現[J].測繪信息與工程，2012，37(2)：10-12.

Influence analysis of double differential and un-differential calculating mode on positioning accuracy

WU Bo1，DANG Yamin2，YANG Qiang2，SONG Chuanfeng2，WANG Danping3

(1.Jiangsu Province Surveying & Mapping Engineering Institute，Nanjing，Jiangsu 210013，China;2.Chinese Academy of Surveying and Mapping，Beijing 100830，China;3.Jiangsu Province Suce Information Technology Co.，Ltd，Nanjing，Jiangsu 211111，China)

Aiming at the problem of the precision difference between double differential network solution mode and un-differential PPP solution mode in high precision data processing，the paper analyzed the positioning accuracy of the same observation data with above-mentioned two modes：the mathematical models of the two modes were elaborated，and an experiment was conducted by using the data of IGS stations around Mediterranean Sea finally.Result showed that the coordinate component difference between the two modes would be about 1～2 cm；when the baseline was short，the baseline length difference in above two modes would be small，the biggest could be about 1 cm，and with the increase of baseline length，the length of baseline differences would show obvious cumulativity；through synthetically comparing between the coordinate components and the baseline length difference，it could be indicated that double differential mode would apply to national CORS net data processing under requirement of high precision，while undifferential mode would be suitable for provincial CORS framework maintenance with the requirement of comparatively low precision.

double differential mode；un-differential mode；location accuracy；baseline

2015-07-30

國家自然科學基金項目(41474011)；中國測繪科學研究院科研業務費支持項目(7771502，7771405)。

吳波(1989—)，男，江蘇鹽城人，碩士研究生，研究方向為高精度GNSS數據處理。

吳波，黨亞民，楊強，等.雙差/非差解算模式對定位精度的影響分析[J].導航定位學報，2016，4(4)：100-103 .(WU Bo，DANG Yaming，YANG Qiang，et al.Influence analysis of double differential and un-differential calculating mode on positioning accuracy[J].Journal of Navigation and Positioning，2016，4(4)：100-103.)

10.16547/j.cnki.10-1096.20160419.

P228

A

2095-4999(2016)04-0100-04