創富路徑
沒有永遠成功的企業,只有適應時代的企業。
農業時代、工業時代和早已到來的商業時代,財富主體的思維方式都是兩分的,即生產者和消費者的界限被明確劃分。許多哲學思想也同樣是以事物二分性為基礎,強調以辯證的角度來看待問題。它,認為矛盾是事物發展的本質,矛盾的存在推動了社會的發展。
經濟學的興起強化了產、消兩類主體的思維方式。基于不同的利益相關方,經濟學家建立包含不同要素的函數來使自身利益最大化。生產者和消費者都想通過降低成本(對生產者來說是生產成本,對消費者來說是支付成本)來最大化自身的效用。如果成本能夠無限降低,低到接近于零,那么即使從商品本身得到的利益是微乎其微的,對于主體來說都是正向收益。正是這種二分性的思維,導致了經濟市場中頻繁出現欺騙、破壞環境等負面行為。
智慧時代趨向于圓體論
然而智慧時代的到來,傳統的二分法思維正在逐步被取代,圓體論的趨勢越來越明顯。東西方傳統文化的差異在于東方強調整體全局的思維方式,而西方則更看重事物的微觀和局部,尤如中醫與西醫的區別。例如,中國文化中有“天人合一”的概念。近現代隨著“西學東漸”運動,西方文化逐步滲入中國。西方思維中主客二分的思維對東方文化產生潛移默化的影響。然而,智慧時代的趨勢已經在暗示“圓”型思考方式是未來發展方向,“圓”也就是無邊界、無差異的意思。
未來的財富創造必然也是向“圓”趨近。商業會逐步地由分立走向一體無分別,在融合后,商業的概念也就消失了。對于企業家而言,最重要的是把握時機。企業家只有把握正確的時機,與時俱進,才能在時代的浪潮中乘風破浪。
因果律告訴我們:整個世界質能是守恒的,有因才會有果。
我們可以把所有的能量劃分為質能、勢能和動能。物理學教授給我們的總能公式如下:
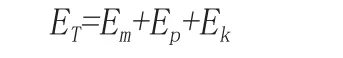
其中ET是總能,而Em是質能,EP是勢能,Ek是動能。
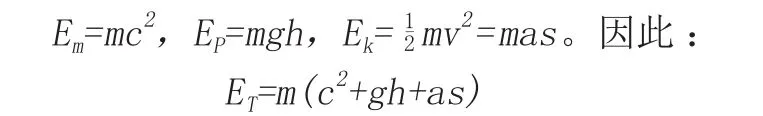
ET的計算式對應了財富的六種要素理論。其中m對應于資源的用度,c對應于互聯網的程度,g對應于客戶的信度,h對應于產品的高度,a對應于科技的密度,s對應于價值的廣度。那么,如何從財富的六種方法來實現財富的創造呢?
m是資源的用度。用度是財富四度論的基礎,如果產品用度為零,其余三度取值再大,該產品的財富值也為零,所以質量相當于產品的用度。
c是互聯網的程度。而c2則表示網絡的交叉程度進一步增加,該網絡包括內外部兩種關系網絡。企業只有將內外部兩張關系網絡營建好,才能擴大受眾面積和影響力。
g表示的是客戶的信度。客戶對公司的產品越信任,公司在消費者心目中的地位越高。
h表示的是產品的高度,也就是產品的質量和服務。對公司而言,接觸消費者的唯一途徑就是公司提供的商品和服務,商品質量越高,服務水平越高,越能得到消費者的認可。
a表示的科技的密度,也就是科技的水平。傳統要素經濟學中,我們就已經知道科技是改變要素邊際收益遞減曲線的重要途徑。科技水平直接對應了企業的創新能力,創新能力越高,企業產品的優勢越大。
s表示距離,意味著價值的廣度,也是企業產品的覆蓋程度。覆蓋面積越大,廣度越大,企業的財富值也就越高。企業按照以上六個方面去做,企業的財富值是無法估量的。
以上的公式是從加法的角度去理解總能這個概念,但是在智慧時代,利用乘法的放大作用可以為企業創造更大的財富。所以我們得到的總能公式是:這里財富的用度被進一步放大,當企業的財富要素值都大于1,上述公式得到的總能相比加法法則可以創造更多的價值。
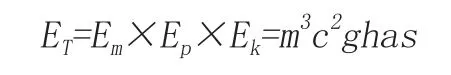
創財需遵循熵增律
智慧時代,企業應該根據財富四度原則來選擇經營的產品,營建企業內外部生態系統,運用科技創新的手段,提供優質的商品和服務,以此增加產品的勢能和在消費者心目中的信度,通過口碑等宣傳以及搭建平臺等方式增加輻射,并處理好以上各部分之間的關系,才能為企業創造更大的價值,贏得更多的財富。
本文給出財富增量的計算公式是:

傳統的財富觀念中要素或資源是財富的根本,因此,傳統財富觀中的創造就是對資源的掠奪,實現個人財富的增值。但是,在這個過程的增值沒有充分發揮人的作用。因此,本文的財富創造是圍繞以下這個公式展開的。

首先毋庸置疑的是,無論是人還是要素本身,基于宇宙的環境下,必然遵循宇宙的熵增律。但是人作為整個財富創造系統的核心,關鍵在于發揮其智慧。智者知道如何利用資源,使各要素各盡其用。經過這一過程的加工,財富創造完成,并得到承載財富增量的載體。
根據質能守恒定律我們可以知道,要素(資源)=質能(載體),這里用實體物質可以衡量測算的。剩下部分中,自然可以得到財富的計算公式是:
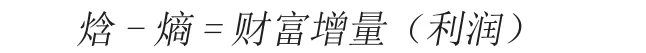
這個公式的本質在于揭示:通過發揮人的聰明才智創造的物質克服了熵增律后,剩余的部分就是財富的增加。
順時而為
習近平總書記在2015年的西雅圖大會上強調了做對的事,任何時機都是好時機,并引用了基辛格博士的話,“評判每一代人時,要看他們是否正視了人類社會最宏大和最重要的問題”。每件事情無所謂對錯,每個企業也無所謂成功,其中的真諦在于合不合時機,合不合時代。
沒有永遠成功的企業,只有適應時代的企業。曾經的輝煌最終成為歷史,只有活在當下,扛著時代的紅旗,才能處于不敗之地。時代或者很嚴苛,它不會因為某個企業是行業的老大,就包容放縱;時代或者很慈祥,只有順從它,它就可以帶領企業越來越壯大。的確,它“吃軟不吃硬”。作為時代的企業,必須要摸清時代的脾性和演變方向,才能永遠成為時代的愛徒。
對于企業而言,目前企業普遍存在的現象是遇到問題,沒有考慮問題產生的原因,而是單純針對問題尋找解決方案,最后容易導致治標不治本。古人常說“當局者迷旁觀者清”,只有跳出這個系統,才能將問題看得更清楚。因此,在遇到問題的時候,關鍵不是在于解決該問題本身,而是判斷問題發生的時代背景,然后明確事情的目標,再選擇解決問題的方法,最后采取行動。
“人無遠慮必有近憂”,我們在自己的人生規劃和發展中重視未雨綢繆和考慮未來的重要性,但是在管理企業時常常忘了判斷未來。“笨鳥先飛”、“早起的鳥兒有蟲吃”,動物也知道為自己多做準備。智慧的人類更應該知道如何取得更好的成績。順應時代者為王,成功者應該是大局的把握者,他洞察經濟、政治、社會環境形勢,制定公司發展的大方向和基本框架,具體的執行細節交給管理者和執行者去展開。
當今社會,習近平總書記提出“創新、協調、綠色、開放、共享”五個新的發展理念,如果企業家不關心國家大事,還要一意孤行,生產高污染高能耗的產品,企業必將走向滅亡。誰摸清了時代發展的根本脈絡,誰才能笑到最后。正如馬丁?路德?金說的那樣“做對的事,任何時機都是好時機”。
對于企業而言,如何順時?順時包括順應:時代×時勢×時機。首先,是時代,企業第一要義是判斷當今的時代和未來的時代;其次,是判斷產業未來的發展趨勢,根據時代來預判企業在未來一年、五年和十年后分別在哪里;最后,則是把握好時間,準確判斷企業應該從哪點入手比較合適。

