非洲某水電站母線豎井圍巖穩(wěn)定分析

劉 寅，馮 飛，屈 潔

(中國電建集團(tuán)西北勘測設(shè)計研究院有限公司，西安 710065)

非洲某水電站母線豎井圍巖穩(wěn)定分析

劉 寅，馮 飛，屈 潔

(中國電建集團(tuán)西北勘測設(shè)計研究院有限公司，西安 710065)

結(jié)合非洲某工程實際，利用PHASE2軟件，通過平面計算和軸對稱計算，對此項目長達(dá)142.3 m的母線豎井進(jìn)行圍巖穩(wěn)定分析。根據(jù)計算結(jié)果，確定不同類別圍巖的支護(hù)形式，為豎井圍巖穩(wěn)定性評價和支護(hù)設(shè)計方案的選擇提供了一種新的方法。關(guān)鍵詞：母線豎井；圍巖穩(wěn)定；支護(hù)形式；有限元計算；PHASE2

0 前 言

隨著水利水電工程的發(fā)展。作為一種典型的廠房結(jié)構(gòu)，地下廠房已經(jīng)日益普遍地出現(xiàn)在各類水電站之中。其中圍巖穩(wěn)定問題是地下洞室中最為突出的問題之一。關(guān)于地下廠房主變的布置，常規(guī)有2種形式，一種將主變布置在平行于主廠房的主變洞內(nèi)，另一種則通過母線豎井將母線引出至地面，接入位于地面的主變。本文以非洲某水電站長達(dá)142.3 m的豎井為模型，通過有限元圍巖穩(wěn)定分析，確定其支護(hù)形式。

PHASE2是由加拿大Rocscience公司推出的巖土專用計算軟件，該軟件主要用于計算邊坡及地下洞室開挖后巖土應(yīng)力、應(yīng)變和位移狀況。軟件特性：可分析平面應(yīng)變問題和空間軸對稱問題；材料的本構(gòu)模型包括了彈性模型、Mohr-Coulomb模型[2]和Hoek-Brown模型[3-4]等備用的模型；可模擬多種具有不同力學(xué)特性的材料；可以進(jìn)行不同開挖階段的模擬[5]；可考慮均勻場力單獨作用[6]、重力單獨作用和二者同時作用下的地應(yīng)力分布[7]；可以對開挖面噴混凝土、開挖面施加錨桿、錨索等支護(hù)加固措施的效果進(jìn)行分析計算[8]。

1 計算思路

以往常用的平面計算只能在二維層面考慮問題，這種情況下，在空間上的問題得不到解決。例如，對于一個豎井，平面計算只能考慮豎井在某一高程、一個特定斷面的結(jié)果，但是無法考慮此斷面高程以上或以下范圍內(nèi)的影響，往往會造成計算結(jié)果偏小。

因此對于圓形的豎井，且四周圍巖類別基本成水平分布，可以考慮用軸對稱計算來模擬此類情況。軸對稱計算是用二維模型來模擬一個關(guān)于某個軸圓周對稱的三維模型。可以用較少的計算資源(二維單元)，模擬三維問題，考慮空間上整個結(jié)構(gòu)的穩(wěn)定性。此計算方法雖然在適用條件上不如平面模型廣泛，但只要滿足其邊界條件，計算結(jié)果較平面模型更加趨于實際情況。

2 母線豎井概況

本工程母線豎井總長142.3 m，外徑7 m，下部連接廠房內(nèi)部母線室，上部連通主變平臺，母線豎井部位地表堆積殘坡積塊石碎石土，結(jié)構(gòu)松散，局部架空，厚度小于15 m，需清除；母線豎井自上而下穿過強風(fēng)化石英黑云母片麻巖和石英巖、中風(fēng)化石英巖以及微風(fēng)化～新鮮的石英黑云母片麻巖，片麻理發(fā)育，片麻理產(chǎn)狀因巖體揉皺而變化較大，主要有NE70°～83°SE∠20°～30°。母線豎井縱向需要穿越強風(fēng)化、中風(fēng)化和弱風(fēng)化3類圍巖。根據(jù)地質(zhì)鉆孔資料顯示，在41.5 m以上為強風(fēng)化；強風(fēng)化與中風(fēng)化之間，有厚度約為1 m的軟弱夾層帶；中風(fēng)化厚度約為33 m，以下均為弱風(fēng)化圍巖。各類圍巖的參數(shù)見表1。對于計算中各種支護(hù)的參數(shù)取值，見表2。

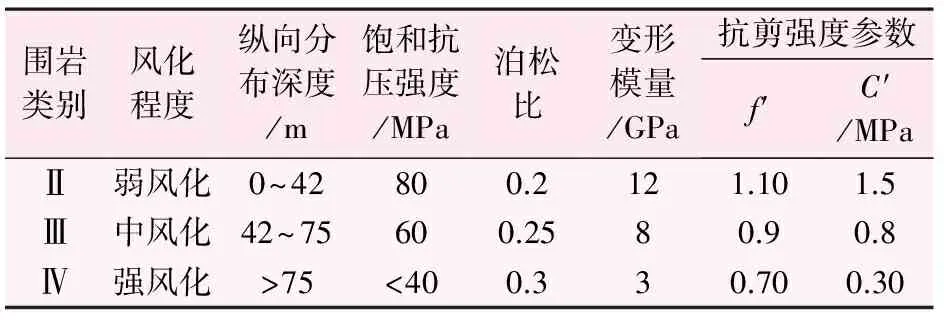
表1 圍巖力學(xué)參數(shù)表

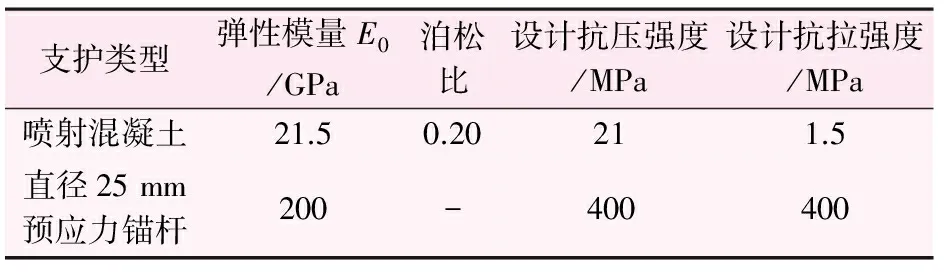
表2 支護(hù)參數(shù)表

初步設(shè)計對于強風(fēng)化圍巖(Ⅳ類圍巖)采取布置長3 m、間距1.5 m、直徑25 mm的錨桿支護(hù)，并設(shè)有100 mm厚掛網(wǎng)噴混凝土；對于中風(fēng)化圍巖(Ⅲ類圍巖)采取布置長3 m、間距2 m、直徑25 mm的錨桿支護(hù)，并設(shè)有100 mm厚掛網(wǎng)噴混凝土；對于弱風(fēng)化圍巖(Ⅱ類圍巖)僅進(jìn)行100 mm厚掛網(wǎng)噴混凝土。

3 平面模型計算結(jié)果

計算使用PHASE2軟件進(jìn)行平面計算，采用摩爾庫倫非線性模型進(jìn)行巖體參數(shù)的定義，計算模型四周采用法向約束。根據(jù)以往的計算經(jīng)驗，當(dāng)計算模型四周的厚度達(dá)到一定程度，就不會對計算結(jié)果產(chǎn)生影響。因此模型在高度方向和長度方向上均取為5倍的豎井開挖直徑，即為40 m。整個模型采用三角形單元劃分，共有節(jié)點2 097個，單元4 354個，計算模型見圖1。

為了計算開挖后圍巖穩(wěn)定性，需要考慮初始應(yīng)力。在平面模型中，計算的初始應(yīng)力由豎向地應(yīng)力得到。根據(jù)圍巖深度的不同，不同類別圍巖計算時的初始應(yīng)力場有所不同。

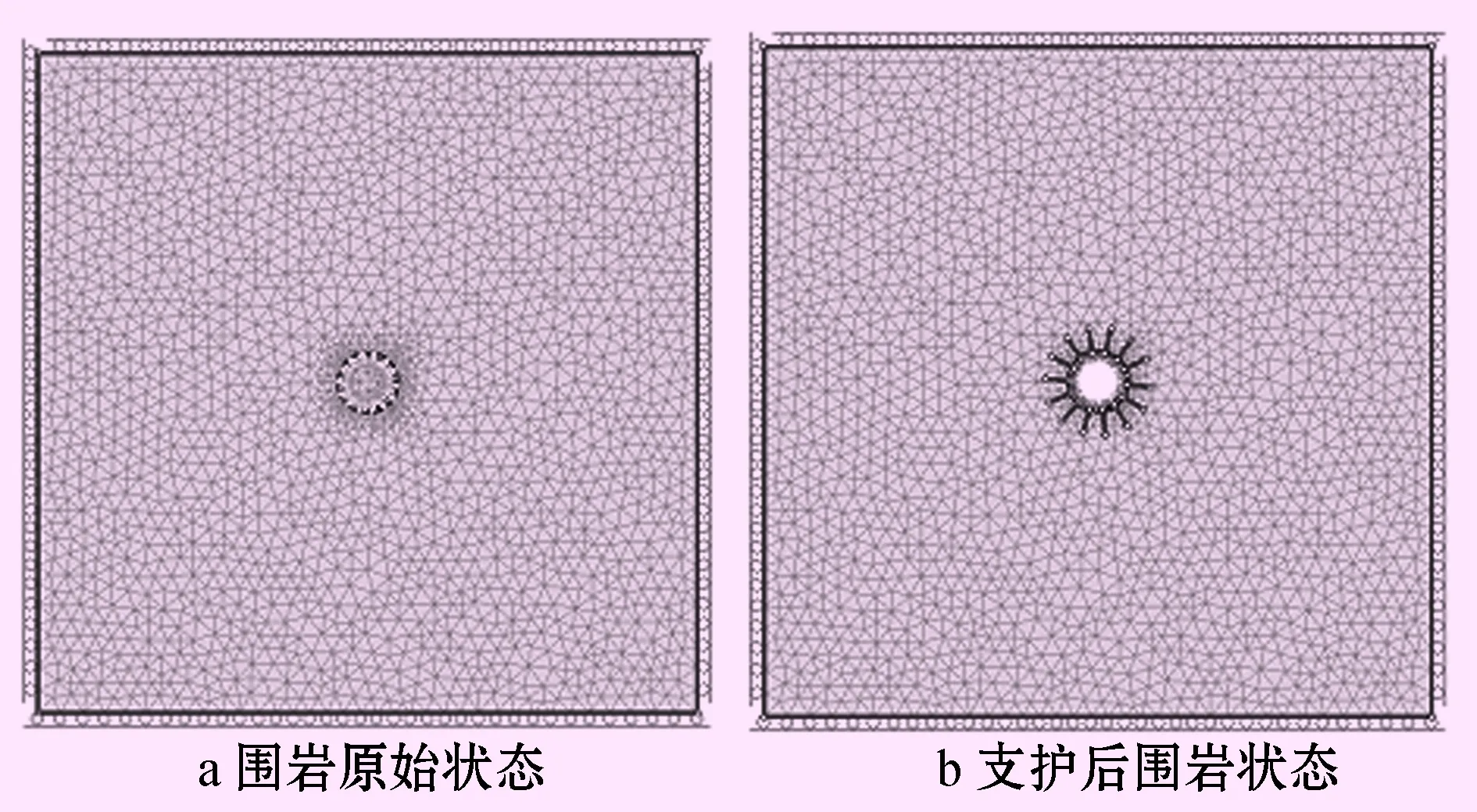
圖1 母線豎井縱剖面圖

根據(jù)圍巖深度，圍巖的豎向應(yīng)力大小為：

(1)

式中：σv為豎向應(yīng)力；γ為巖石容重；H為巖體深度。

水平向圍巖壓力為：

(2)

式中：σh為豎向應(yīng)力；μ為巖石泊松比。

計算模型輸入各類荷載和支護(hù)條件后，其計算結(jié)果分析如下：

(1) 強風(fēng)化圍巖在有支護(hù)的情況下，出現(xiàn)的最大壓應(yīng)力為0.76 MPa，遠(yuǎn)小于圍巖的強度。豎井的最大位移值為0.45 mm，此數(shù)值很小。因此認(rèn)為對于強風(fēng)化圍巖，其支護(hù)形式的選取能夠滿足要求，圍巖在支護(hù)后穩(wěn)定。

(2) 中風(fēng)化圍巖在有支護(hù)的情況下，出現(xiàn)的最大壓應(yīng)力為1.17 MPa，遠(yuǎn)小于圍巖的強度。豎井的最大位移值為0.28 mm，此數(shù)值很小。因此認(rèn)為對于中風(fēng)化圍巖，其支護(hù)形式的選取能夠滿足要求，圍巖在支護(hù)后穩(wěn)定。

(3) 弱風(fēng)化圍巖在有支護(hù)的情況下，出現(xiàn)的最大壓應(yīng)力為1.8 MPa，遠(yuǎn)小于圍巖的強度。豎井的最大位移值為0.3 mm，此數(shù)值很小。因此認(rèn)為對于弱風(fēng)化圍巖，其支護(hù)形式的選取能夠滿足要求，圍巖在支護(hù)后穩(wěn)定。

根據(jù)以上計算結(jié)果分析，圍巖開挖后，無論是第1主應(yīng)力還是第2主應(yīng)力的數(shù)值都不大，且圍巖的變形值很低，并且塑性區(qū)幾乎不可見。因此認(rèn)為支護(hù)設(shè)計基本合理，圍巖在開挖后不存在失穩(wěn)的危險。

4 軸對稱模型計算結(jié)果

軸對稱計算模型，可以用二維模型來模擬一個關(guān)于某個軸圓周對稱的三維模型。這種計算比二維平面計算要更加準(zhǔn)確，特別是能夠反映在不同高度下圍巖的穩(wěn)定特性。

根據(jù)實際設(shè)計的母線豎井，建立軸對稱模型，對稱軸為母線豎井中心線。

計算的材料依然使用摩爾庫倫模型，模型底部和兩側(cè)都使用法向約束。

通過計算結(jié)果可以看出，最大壓應(yīng)力為5 MPa，遠(yuǎn)小于圍巖的強度。豎井的最大位移值為3 mm，此數(shù)值很小。因此認(rèn)為對于強風(fēng)化圍巖，其支護(hù)形式的選取是能夠滿足要求的，圍巖在支護(hù)后是穩(wěn)定的。

對比平面計算結(jié)果，軸對稱模型計算的結(jié)果相對較大，但總體數(shù)值比較接近，所得結(jié)論也是一致的。此類計算結(jié)果同圍巖參數(shù)、豎井的深度和直徑關(guān)系密切，可以看出，如果僅考慮平面計算結(jié)果，在一些地質(zhì)條件較差、地應(yīng)力較大的區(qū)域，也許會得到與實際情況相違背的結(jié)果。但通過軸對稱計算，可以充分地反映出三維空間上圍巖的穩(wěn)定性，其計算結(jié)果要更加真實。

5 結(jié) 語

根據(jù)平面和軸對稱模型的計算結(jié)果，對于圍巖進(jìn)行的支護(hù)設(shè)計是合適的，能夠滿足安全要求。此工程中，雖然2種計算所得結(jié)果相同，但可以看出軸對稱模型計算結(jié)果較平面模型計算結(jié)果大。這種大是考慮了三維空間影響得到的結(jié)論，是合理的，更加趨向于真實的情況。

平面計算模型可以在任何條件下使用，其適應(yīng)性較強。而對于軸對稱模型，首先必須是圓形隧洞，并且在周邊是對稱的，一旦在計算范圍內(nèi)有其他洞室存在，就無法考慮這些因素，會使得計算的邊界條件不準(zhǔn)確，無法保證計算結(jié)果的真實性。

因此，在后續(xù)工程中，在滿足軸對稱模型計算邊界條件要求的前提下，使用此種計算能夠更加真實地反映實際情況。如果邊界條件不能夠滿足，可以用平面模型作為基本計算，軸對稱計算作為復(fù)核計算，在相互驗證之后，找到最為經(jīng)濟(jì)和合理的支護(hù)設(shè)計，從而收到良好的經(jīng)濟(jì)效益。

[1] 華東水利學(xué)院.巖石力學(xué)[M].北京：水利電力出版社，1986.

[2] 韓瑞庚.地下工程新奧義[M].北京：科學(xué)出版社，1987.

[3] HOEK E，BROWN E T. Practical estimates of rack mass strength[J].International Journal of Rock Mechanics and Mining Science，1998,38(08):1165-1186.

[4] R.K.Goel，Bhawani Singh.Rock mass classification [M].ELsevier Science Ltd，1999.

[5] 李杰,郭海燕,劉凌云,牟桂杰.丈八口隧道圍巖穩(wěn)定分析[J].巖土力學(xué)，2004(S2)： 537-541.[6] 王立忠,胡亞元,王百林,陳云敏.崩塌松散圍巖隧道施工穩(wěn)定性分析與監(jiān)控[J].巖石力學(xué)與工程學(xué)報，2003,22(04)：79-85.[7] 何欣,曹懷園,劉永智,劉潔玉.Phase2軟件在隧洞開挖圍巖支護(hù)時機(jī)中的應(yīng)用[J].西北水電，2015(03)：57-61.

[8] 溫森,楊圣奇.基于Hoek-Brown準(zhǔn)側(cè)的隧洞圍巖變形研究[J].巖土力學(xué)，2011,32(01)：70-76.

[9] 高凱,王林維，郭建宏.云南某水電站地下洞室圍巖穩(wěn)定性分析[J].西北水電，2015(05)：33-37.

[10] 石高峰.基于Phase2的地下廠房及尾調(diào)室開挖與支護(hù)設(shè)計[J].水力發(fā)電，2015(12)：63-67.

Analysis on Stability of Surrounding Rock of Basbar Shaft

LIU Yin, FENG Fei, QU Jie

(Northwest Engineering Corporation Limited, Xi'an 710065,China)

In combination with the practice of one African project and by application of PHASE 2 software, stability of the surrounding rock of the 142.3 m long busbar shaft of the project is analyzed through plan calculation and axis symmetry calculation. According to the calculation results, supports modes for different surrounding rocks are finalized, this provides stability assessment and support design scheme of the shaft surrounding rock with a new method.Key words:basbar shaft; stability of surrounding rock; support mode; calculation by finite element method; PHASE2

1006—2610(2016)06—0094—03

2016-11-18

劉寅(1987- )，男，河北省秦皇島市人，助理工程師，主要從事水利水電工程設(shè)計工作.

TV554;TU457

A

10.3969/j.issn.1006-2610.2016.06.024