泵站出水管道水錘風險分析

郭 強，王長新

(新疆農業大學 水利與土木工程學院，新疆 烏魯木齊 830052)

泵站出水管道水錘風險分析

郭 強，王長新

(新疆農業大學 水利與土木工程學院，新疆 烏魯木齊 830052)

本文結合新疆某水泵出水管道針對水泵出水管道水錘風險問題進行了分析。對比有無箱式雙向調壓塔出水管初始端水錘壓力，管道測壓水頭進行了對比，表明了箱式雙向調壓塔的調壓效果好。建立水錘風險計算的功能函數，水錘作為不確定性變量，運用蒙特卡洛法對無箱式雙向調壓塔和箱式雙向調壓塔安裝安裝于出水管的水錘風險進行定量分析。結果表明，安裝調壓塔，管道風險最大處風險值降低13倍。

泵站;水錘;不確定性;風險

DO I:10.3969/j.issn.1672-2469.2016.08.032

在泵站管道工程中，由于人為或者機械的原因導致機組失去動力，在慣性作用下，流體繼續流動，且流量逐漸減小，導致管道壓強低于汽化壓強，在外荷載作用下，產生較大風險。當流速減小至零時，水流回流，產生彌合水錘，彌合水錘壓力往往是正常工作水壓的幾倍甚至幾十倍，使管道產生巨大的環向應力［1，2］。這種水錘壓力就產生了較大的風險。并且造成的后果小到設備損壞、漏水，大至泵站淹沒、人員傷亡。根據泵站水錘研究證明，風險的危害是不可預測的，努力地減小風險或者減小風險后的損失是有必要的［3～8］。在國內外眾多專家學者的努力下，減小停泵水錘風險有了長足的發展。本文依托新疆小紅山水泵出水管道，對水泵出水管道水錘風險進行定量計算分析。

1 工程簡介

管道前接泵站，泵站電動機額定功率 13500 KW，額定轉速600 r/m in，額定效率89%，安裝高程516.55m，泵型為立式單級單吸離心泵，安裝高程516.55m，水泵設計揚程為186m;管道后接水池，管出口中心離水面1.03m。管道全長12790m，水泵后出水管道由前段6900m涂料鋼管，簡單管管徑2.2，壁厚22mm，與后段5890m PCCP管組成，每隔500m設置排氣閥。采用單溝雙管寬槽式埋設，機械開挖，邊坡1∶1，管頂覆土4～6m。坡度0.009～0.018。每隔532.92m進行斷面編號，水泵出水管初始位置編號為1，管道末端編號為25。時間段32秒內水力瞬變。閥門相對開度按直線規律1—t/tz進行關閉。

2 水錘計算

特征線法是水錘數值計算最常用方法［9］。易于編程，可處理較為復雜的管道，實用范圍廣且能夠滿足實際工程中的精度要求。根據水力瞬變的連續方程與運動方程有限差分得正特征線方程C+:

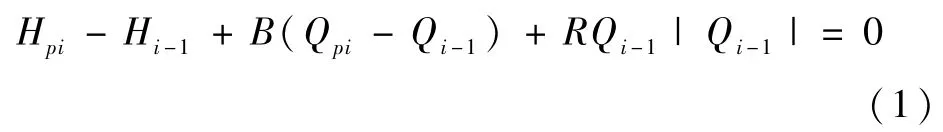
負特征線方程C+:

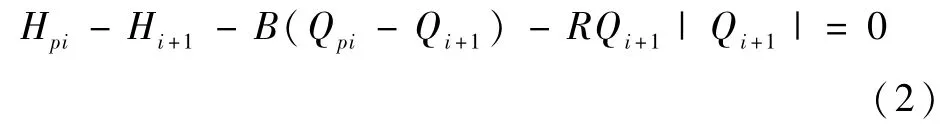
a為水錘波波速，對給定管道波速為常數，m/s;E、K為材料彈性模量和流體體積彈性模量，Mpa;D、e為管道直徑與壁厚，mm;ρ為流體密度，kg/m3;在本工程中溫度變化小視為常數。Hi+1、Qi+1分別為斷面編號i+1在t時刻時水錘壓力水頭和流量，m，m3/s;Hi-1、Qi-1分別為斷面編號i-1在t時刻時的水錘壓力和流量;HPi、QPi分別為斷面編號i在t+Δt時刻水錘壓力和流量。把整個管道等分間距為 Δx，時間間隔為 Δt，Δx=aΔt。

相對壓力水頭h=H/Hn，q=Q/Qn其中Q、H為流量和水錘壓力水頭計算值，Qn、Hn為正常狀態下泵站出水管道設計流量和設計水頭。相對流量泵站出水管道結果如圖1所示，由于泵站機組突然失去動力，在慣性作用下繼續流動，但流量減小。此時管道內產生漸漸空腔，導致管道內壓強減小。當流體速度減為0時后，流體回流，由于逆止閥的存在，流體止于逆止閥前完全填補空腔，造成水柱彌合，產生彌合水錘。水錘壓力水頭是正常工作水壓水頭的-0.39～1.9倍。

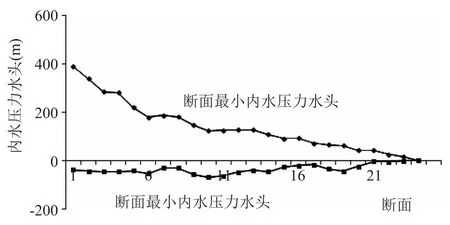
圖1 無調壓塔水錘壓力水頭和流量的變化

在水錘現象的影響下，計算各斷面表征各的測壓管水頭峰值和最小值包絡計算結果如圖2所示。由圖可以看出，在水錘現象的影響下，壓力通過波的形式傳遞，導致測壓管水頭峰值在0～5斷面都很高，且呈減小趨勢。當水錘波到達管道末端水池時，在水池中形成減壓波，向閥門傳遞。造成各斷面處均小于設計壓力，并成減小趨勢。

3 水錘風險的估算

計算水錘風險時，水錘壓力作為不確定性變量，各斷面水錘壓力峰值為均值，標準差為均值0.05倍的正態分布，建立水錘風險計算模型。

3.1 產生符合分布的隨機數

從理論上講，只要有了任何一種連續分布的隨機數，就可以通過多種方法，產生其它分布的隨機數。由于［0，1］區間上的均勻分布是最簡單、最基本的連續分布，所以通常都使用［0，1］上的均勻分布隨機數。

通常用同余法產生［0，1］區間上的均勻分布:

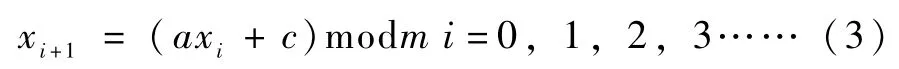
式中a為乘子，c為增量，m為模。a，c，m均為非負整數，a，c都小于m。得到ui=xi/m、u1、u2為［0，1］上兩個均勻分布隨機數，則經過下列變換就可以得到標準正態分布N(0，1)上的兩個隨機數Ni、Ni+1:

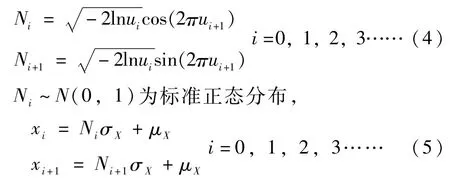
x～N(μX，σX)為一般正態分布。

3.2 不確定隨機變量

統計研究表明，鋼材強度 σR服從正態分布，變異系數為0.095［10］。由于各種原因，計算內水壓力、材料參數等變量具有不確定性，且無相關數據進行數理統計分析。根據誤差理論、中心極限定理和王長新等人的研究，將難以確定的分布視為正態分布，并且認為均值為設計值，標準差按均值的5%選取。水錘壓力計算結果為均值，相對標準差取0.05。隨機變量的分布特性與統計特征值見表 1［11～13］。

表1 主要隨機變量的分布特性與統計特征值

3.3 極限狀態方程

本工程管道坡度為0.0094～0.018，小于《給水排水工程管道結構設計規范》規定的36%，不考慮管道軸向應力的影響。根據文獻建立其功能函數［14］。

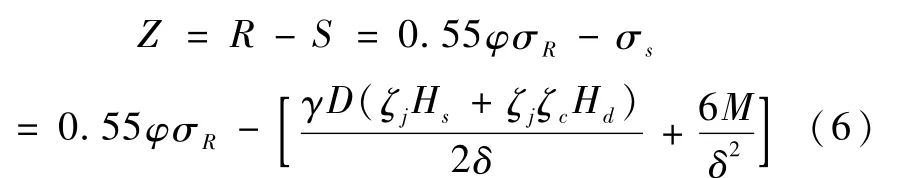
式中:M=K1Wr2m-0.083eΔX-K1PΔXrm;ΔX=ζj—相對前池水頭;其中W—土壓應力;rm—管壁半徑;△X—水平撓度; K—管底支承角相關的系數;e—被動土壓力系數; EP—鋼的彈性模量;I—單位長度鋼管管壁慣性矩。Hmax—最大水頭;Hs—設計水頭;Hc—水錘設計值;Z—管道高程;σs—管道所受環向應力。對于PCCP管，目前沒有明確的規范標準，但大量實驗表明，PCCP管抗裂失效主要是混凝土開裂引起，其環向應力由內水壓力和土壓力引起［15］。利用軟件ABAQUS對管道環向應力進行計算。網格的劃分如圖2所示。

圖2 PCCP網格圖

計算得混凝土環向應力如圖3所示。

圖3 PCCP混凝土環向應力

建立其功能函數:

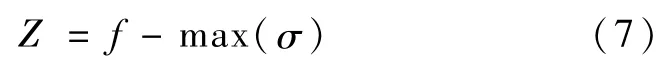
式中:f為管道抗拉強度，σ為ABAQUS計算環向應力，其后PCCP每小段計算相類似。基于MATLAB的蒙特卡洛，計算100萬次的結果如圖5所示由于鋼管屈服強度遠遠大于內水壓力，故產生的風險值較小;到斷面編號為15處管道變為PCCP管，PCCP管混凝土抗拉強度較小，造成水錘風險值在斷面編號為15處突然升高(PCCP管與鋼管接口)，其后由于出水池影響，水錘壓力峰值減小、不出現負壓情況，所以風險值也減小［16～17］。

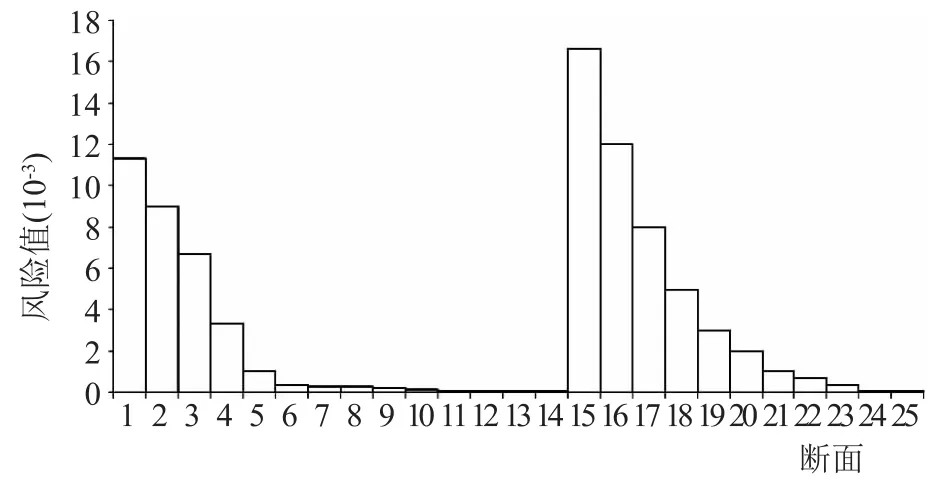
圖4 無調壓塔各斷面風險

4 調壓后水錘風險估算

4.1 靈敏度驗算

利用調節水錘壓力減小風險措施時，必須驗證水錘壓力不確定性的影響。取設計標準差0.5～1.5倍，其他變量不變，利用蒙特卡洛模擬得出主要不確定因素與風險關系，如圖5、圖6所示。兩圖土壓力的不確定性對風險值的影響很小，幾乎可看作確定性變量。當水錘壓力標準差小于設計標準差時，水錘壓力的不確定性對風險值影響較小，但當水錘壓力標準差大于設計標準差時，水錘不確定性對風險值影響較大并越來越大。由此可見，水錘壓力設計標準差的選取就尤為重要。鋼管材料參數和焊縫系數的不確定性對風險影響很小，計算時視情況適當考慮。PCCP管段由于混凝土抗拉強度內水壓力不確定性對風險影響遠大于有效預應力不確定性對風險影響，故混凝土抗拉強度和內水壓力作為不確定性變量。

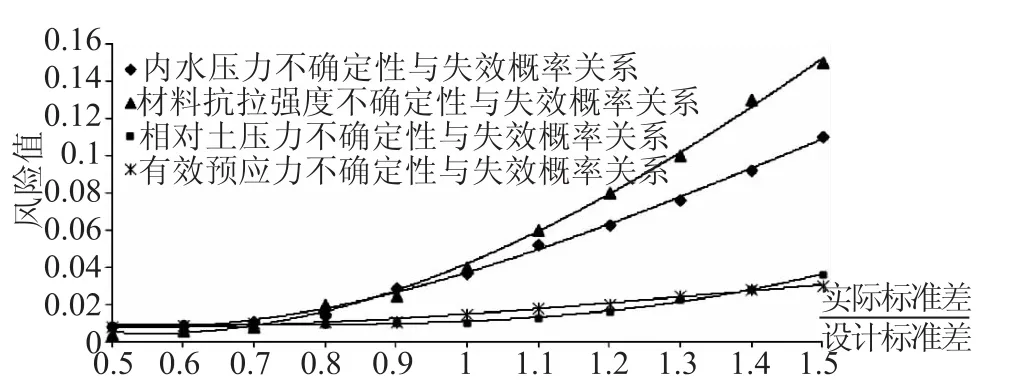
圖5 鋼管主要變量不確定性對風險影響

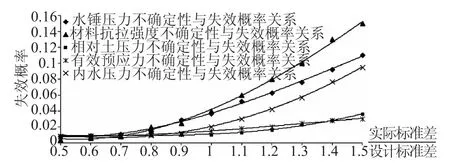
圖6 PCCP主要變量的不確定性對風險影響

驗證了減小風險產生主要不確定荷載為水錘壓力，為減小水錘風險值，應對水錘壓力進行調節。

4.2 箱式雙向調壓塔原理

箱式雙向調壓塔采用了上下不等面積活塞增壓的原理。雖然箱式雙向調壓塔內的壓強遠小于管道內的壓強，但由于壓力F等于壓強P與面積S的乘積，而活塞的上部面積遠大于下部面積，活塞受力依然可以達到平衡。兩個值的大小決定箱式調壓塔的動作狀態，箱式雙向調壓塔的有效高度就決定于活塞上下面積的比值。

(1)當管道壓強乘以下部小活塞面積等于箱式雙向調壓塔內的水壓乘以上部大活塞面積時，活塞處于正常關閉狀態，調壓塔既不向管道注水，管道水流也不進入調壓塔。

(2)當管道壓強乘以下部小活塞面積大于箱式雙向調壓塔內的壓強乘以上部大活塞面積時，活塞整體向上運動，處于管道高壓開啟狀態，管道水流進入調壓塔。

(3)當管道內水壓力小于箱式調壓塔內水深的時候，調壓塔的單向板向下打開，活塞處于管道低壓注水狀態，調壓塔向管道內注水。

4.3 調壓效果計算

調壓后，水泵出水管道初始位置水錘壓力變化如圖所示，對比圖1和圖2水錘峰值由正常工作壓力的1.96倍降為1.3倍，水錘最小值由低于汽化壓強正常工作壓力的倍增為0.2;管道測壓水頭波動得到很大的減小，沒有低于汽化壓強情況出現。證明了箱式雙向調壓塔具有很好的效果。

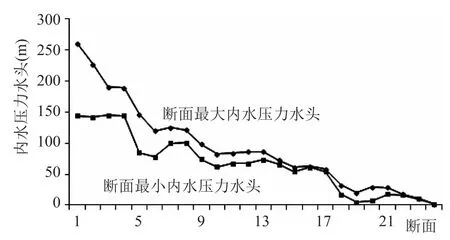
圖7 有調壓塔內水壓力水頭變化

如表2所示，調壓前后第15斷面風險值減小了13倍，證明箱式雙向調壓塔對供高本工程可靠度有很好的作用。

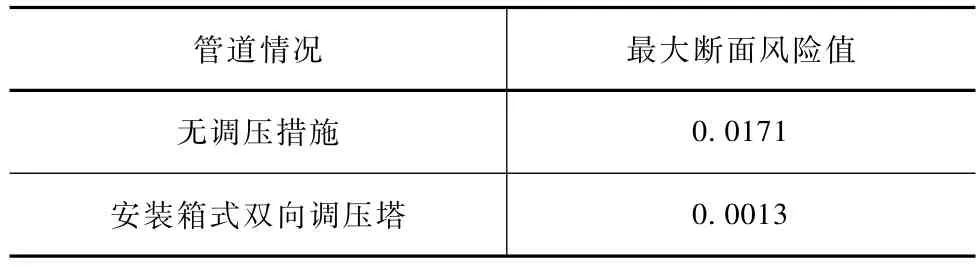
表2 第15斷面調壓前后風險值對比

5 結論

(1)通過蒙特卡洛無調壓塔情況下風險模擬，得到管道風險最大為鋼管與PCCP管接口處。且計算水錘風險時，水錘和內水壓力作為不確定性變量，土壓力可視為確定性變量。

(2)對比安裝箱式雙向調壓塔和無調壓塔，得到箱式雙向調壓塔在本工程削減彌合水錘峰值、控制水錘壓力出現負值效果很好。安裝調壓塔后，最危險斷面風險值減小近13倍。

［1］喬丁.高揚程多起伏長距離壓力輸水管道水錘防護技術研究［D］.西安.長安大學，2010.

［2］岳文青.長距離輸水工程中采用箱式雙向調壓塔進行水錘防護的實驗研究［D］.西安.長安大學，2009.

［3］蔣紅梅，陳松山，何鐘寧.泗陽泵站出水流道可行性方案對比分析研究［J］.水利與建筑工程學報.2011，9(01):104-109.

［4］周濟人，金燕，劉超.大型泵站箱形進水流道內部流動數值模擬［J］.水利與建筑工程學報.2011，9(06):48-50.

［5］楊杰.結構可靠度計算方法及靈敏度分析研究［D］.大連.大連理工大學，2012.

［6］沈士明，趙建平.壓力管道的風險分析技術［C］.第三屆全國管道技術學術會議壓力管道技術研究進展精選集，合肥:2006.

［7］金明.水力不確定性及其在防洪系統風險分析中的影響［J］.河海大學學報，1991，19(01):40-45.

［8］羅云，樊運曉，馬曉春.風險分析與安全評價［M］.北京:化學工業出版社，2004.

［9］李玉科.排水系統取消逆止閥的電算方法［J］.水利學報，1989 (05):55-70.

［10］吳世偉，張思俊，余強.壩上游水位變化規律及統計量［J］.華東水利學院報，1984(04):66-71.

［11］趙國藩.工程結構可靠性理論與應用［M］.大連:大連理工大學出版社，1996.

［12］楊惠蓮，張濤.誤差理論與數據處理［M］.天津:天津大學出版社，1992.

［13］王長新.施工導流風險分析及計算［D］.南京.河海大學，1995.

［14］GB50332-2002.給水排水工程管道結構設計規范［S］.

［15］王玉良.預應力鋼筒混凝土管受力性能的理論研究［D］.天津.天津大學，2007.

［16］張虎，王長新，李江，等.基于MATLAB的MC法在施工導流風險率計算中的應用［J］.水利與建筑工程學報 2013，110 (04):94-97.

［17］尤嘉惠，王長新.基于蒙特卡羅法的挑流消能風險分析［J］.水利與建筑工程學報，2015，13(04):146-150.

［18］陳利瓊，張鵬，馬劍林，等.基于故障樹的油氣管道失效概率模型［J］.石油工業技術監督，2006(10):11-15.

［19］楊開林.電站與泵站中的水力瞬變調節［M］.北京:中國水利水電出版社，2000.

TV732.4+1

A

1672-2469(2016)08-0100-04

2016-04-13

郭 強(1989—)，男，碩士研究生。