基于初始缺陷的鉆柱疲勞壽命預測方法

耿亞楠陳孝亮楊進劉書杰鄧賀何英明

1.中海油研究總院；2.中國石油大學（北京）

基于初始缺陷的鉆柱疲勞壽命預測方法

耿亞楠1陳孝亮2楊進2劉書杰1鄧賀2何英明1

1.中海油研究總院；2.中國石油大學（北京）

鉆柱初始缺陷是影響鉆柱疲勞壽命的關鍵因素之一。傳統的鉆柱疲勞預測模型往往忽略初始缺陷的影響，導致預測的結果偏大，影響鉆柱的安全性。針對鉆柱的初始缺陷，在傳統無缺陷鉆柱的受力研究基礎上，用應力集中系數修正鉆柱受到的拉伸應力和彎曲應力，同時根據鉆柱裂紋拓展規律建立鉆柱的疲勞壽命預測模型，最后利用有限元分析工具分別模擬具有不同深度、半長和位置的初始缺陷的鉆桿和無缺陷鉆桿的平均應力及最小疲勞壽命，并進行對比。研究結果顯示，初始缺陷深度和半長對鉆桿的最小疲勞壽命有著重要的影響，初始缺陷離接箍越近，對鉆柱的疲勞壽命的影響越大。研究結果為準確預測鉆井過程中鉆柱疲勞壽命，從而保證安全、高效鉆進，具有一定的指導意義。

鉆柱疲勞壽命；應力集中系數；初始缺陷；有限元模擬；最小疲勞壽命

隨著海上油田的開發井型由直井等的單一模式向大斜度井等復雜結構模式轉變。鉆柱由于中和點高、受壓段長、承受扭矩高和作業時間長的特點，受到自身運動以及井下載荷作用，常常過早失效（李文飛，2008）［1］。

目前國內外學者針對鉆柱的疲勞壽命進行了一系列研究，M.Veidt（2004）［2］根據提出的鉆桿疲勞壽命試驗臺，總結了鉆桿公扣圓周上的裂紋拓展規律；B.A.Dale（1988）［3］通過實驗的方法研究了鉆桿接箍類型、初始裂紋等對鉆桿壽命的影響，其結果對鉆桿無損探傷周期有著重要指導意義；羅增［4］等針對空氣鉆井中鉆柱振動頻率高、疲勞損壞嚴重的問題，修正了鉆柱軸向應力和疲勞裂縫計算公式；李文飛（2008）［1］等結合Forman模型建立了鉆柱Ⅰ，Ⅲ復合型疲勞裂紋拓展速率計算模型；高寶奎（2003）［5］重點討論了鉆柱壽命的不確定因素，包括工作環境、工作載荷的不確定性等。

筆者在前人研究的基礎上，采用應力集中系數修正鉆柱井下受到的軸向拉伸應力和彎曲應力，通過應力集中系數描述了初始缺陷對平均應力和最小疲勞壽命的影響程度，同時優化了鉆柱疲勞壽命預測模型，為海上的鉆井作業提供了安全保障。

1 初始缺陷下的鉆柱應力分析

Stress analysis on string with initial imperfection

鉆柱在使用前或使用過程中產生的缺陷，如焊接點、腐蝕區、卡瓦壓痕等，作為裂紋源，是影響鉆桿疲勞壽命的重要因素。傳統以無缺陷鉆桿為假設條件得出的鉆柱應力分析以及鉆柱疲勞壽命模型并不能夠準確描述實際情況，風險性高，需要進行修正。

定義應力集中系數Rscf（Stress Concentration Factor，SCF），即集中應力與施加應力的比值來修正原有的鉆柱應力［6］。

如圖1，應力集中系數隨壓痕深度呈幾何倍數增大［7］。一般而言，缺陷的深度為0.001～0.01 in，應力集中系數取值為1.1～1.6。

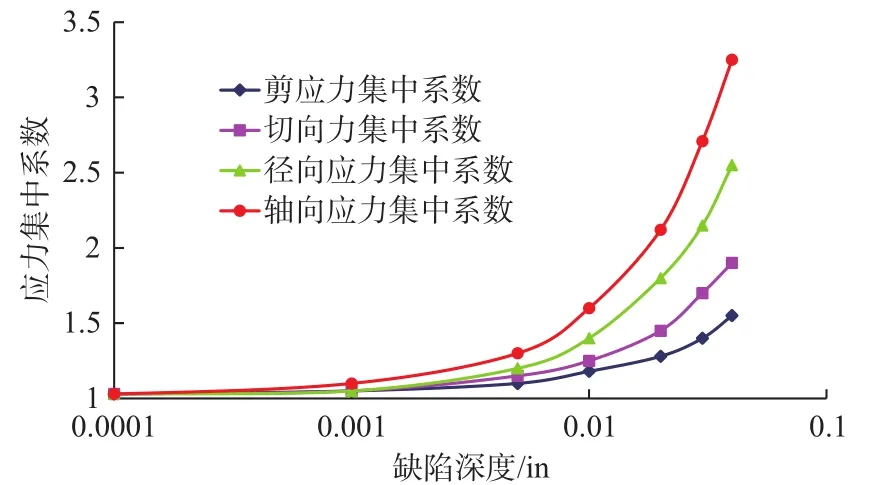
圖1 缺陷深度與應力集中系數關系Fig.1 Relationship of imperfection depth and stress concentration factor

根據缺陷深度，查圖版得應力集中系數Rscf，與σb和σa相乘得修正的σbc和σac。

由于鉆柱受到的力基本都是作用在鉆桿上，關于軸向拉伸應力和彎曲應力，可以用鉆桿的受力代替。同時為研究鉆柱初始缺陷的影響，在此不考慮使用過程中產生的缺陷影響。

（1）修正后的軸向拉伸應力。在大斜度井中，由于井斜角較大，旋轉中的彎曲鉆桿交替受壓、受拉，加劇了裂紋張開、擴展的速度，降低了鉆桿的抗疲勞能力。考慮鉆桿自重影響，忽略鉆桿受到的大鉤載荷、鉆壓等因素的影響，鉆桿在井斜段承受的拉伸載荷為

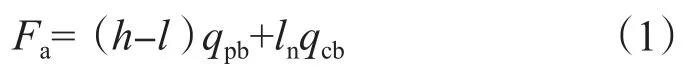
式中，Fa為拉伸載荷，N；h為最大井深，m；l為某截面所在的測深，m；ln為中和點距鉆鋌頂部的距離，m；qpb為單位長度鉆桿在鉆井液中的重力，N/m；qcb為單位長度鉆鋌在鉆井液中的重力，N/m。

此時的拉伸應力為

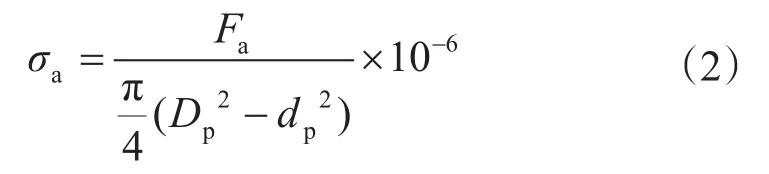
式中，σa為拉伸應力，MPa；Dp為鉆柱外徑，m；dp為鉆柱內徑，m。

考慮初始缺陷的影響，用應力集中系數修正軸向拉伸應力，得到

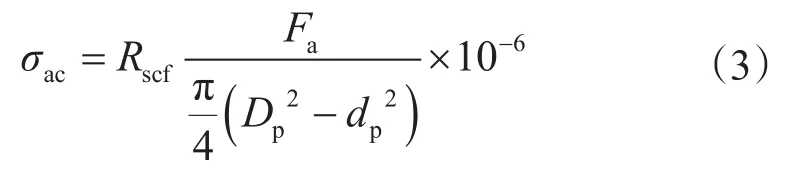
（2）修正后的彎曲應力。鉆桿彎曲應力是由橫向振動沿多接觸點鉆桿傳播而引發的。除正常轉動外，鉆桿會在井內逆時針繞井眼軸線旋轉。彎曲應力的大小取決于反轉速度，而且自轉加大了彎曲頻率，彎曲頻率與正、反轉速之和相近（韓家強，2014）［8］。如果不考慮鉆具進動的影響，則接頭貼近井壁而本體與井壁不接觸時，鉆桿的彎曲應力為

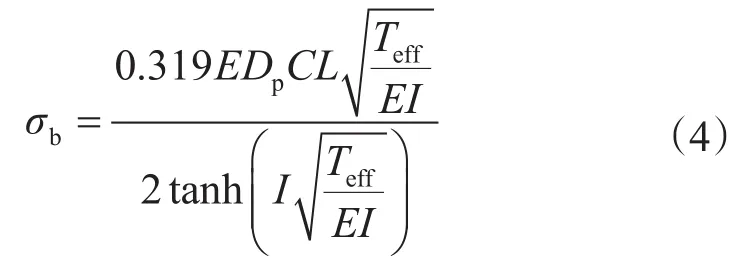
式中，σb為彎曲應力，MPa；E為彈性模量，MPa；C為狗腿度，rad/mm；L為接箍間的鉆桿半長，mm；I為鉆桿截面慣性矩，mm4；Teff為截面下鉆柱的浮重，kg。

考慮初始缺陷的影響，用應力集中系數修正彎曲應力，得到

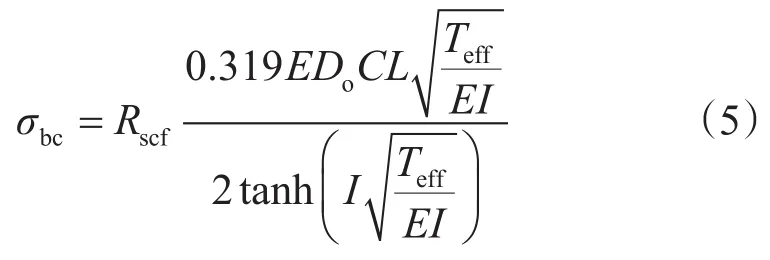
最后計算修正應力σad，增加了應力集中效應和軸向拉伸力的影響

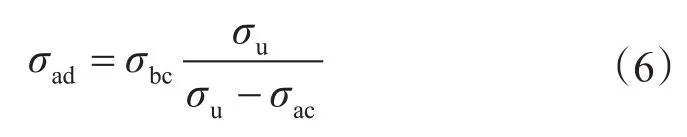
式中，σu為鉆桿材料的抗拉強度。進而用修正應力σad作為最大彎曲應力σ來計算疲勞壽命。

考慮初始缺陷影響后，相對于無缺陷情況，鉆柱的應力水平提高，裂紋擴展速率加快，疲勞壽命會更接近實際情況，偏于安全。

鉆柱通過彎曲井眼時，所受的應力會在大小和方向上發生交替變化［9］，在交變的彎曲應力和拉應力的共同作用下，鉆柱的等效應力可以通過Mises等效應力理論［10］來進行應力合成，根據第四強度理論，可得等效應力為

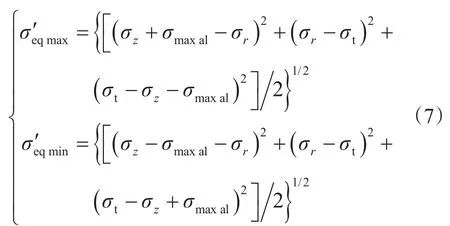
Tresca等效應力為

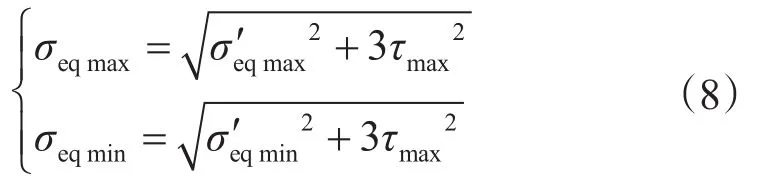
因此平均應力與應力幅為

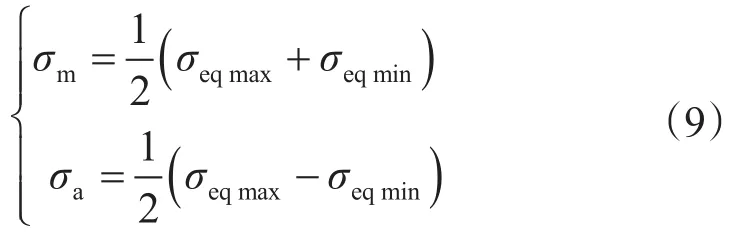
2 鉆柱疲勞壽命預測模型

Prediction model on fatigue life of string

考慮到鉆柱的初始缺陷影響，所以在疲勞壽命計算中，需要先計算出裂紋的幾何形狀因子以及應力強度因子［11］，并由無損探傷測定初始裂紋尺寸，再根據應力條件求得臨界裂紋尺寸，最后根據Walker模型求出裂紋疲勞壽命［4］。

考慮到鉆桿在制造及使用中產生的裂紋多為表面線性裂紋［4］，其幾何形狀因子計算公式為

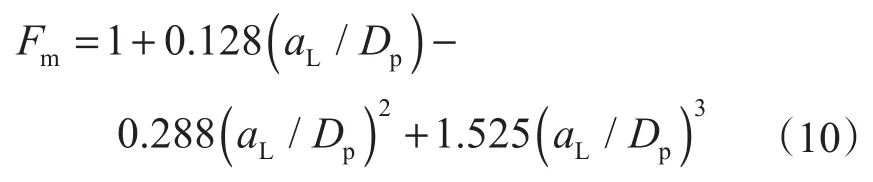
式中，Fm為裂紋形狀因子；aL為裂紋半長，m。

最大應力強度因子為

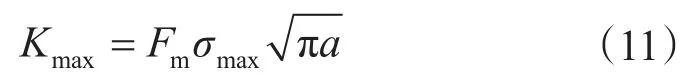
B.A.Dale通過全尺寸試驗發現鉆桿表面裂紋的形狀為半橢圓形［3］，隨著裂紋的擴展，橢圓中心逐漸遠離裂紋初始點，裂紋的半長aL和深度a關系為

鉆桿的初始裂紋尺寸a0可由無損探傷測出，而其臨界裂紋尺寸ac則由其受力情況和材料性能決定

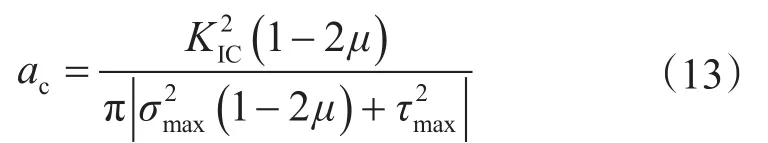
式中，ac為鉆桿在某應力條件下的臨界裂紋深度，m；KIC為材料斷裂韌性，MPa·m1/2。

Walker模型

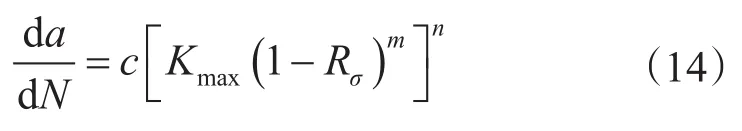
式中，a為裂紋深度，m；N為應力循環次數，周；Kmax為最大應力強度因子，MPa·m1/2；Rσ為應力比；c、m、n為材料常數。

在鉆柱恒幅加載的條件下，裂紋從初始裂紋a0擴展到臨界裂紋ac所經歷的循環周次N為

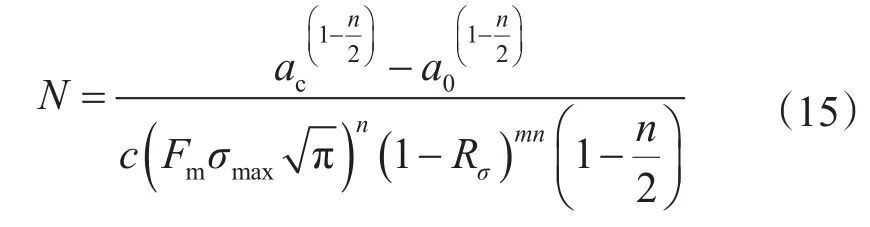
3 鉆桿疲勞有限元分析

Finite element analysis on the fatigue of string

利用Ansys Workbench工具，模擬了無缺陷鉆桿和受初始缺陷深度、初始缺陷半長、初始缺陷位置3個因素影響下的鉆桿所受的平均應力以及最小疲勞壽命，并通過繪制曲線圖進行對比。

3.1 模型建立

Model establishment

（1）模型材料參數。有限元模型的材料選為鋼材，參數如下見表1。

表1 模型材料參數Table 1 Material parameters of the model

（2）鉆桿參數。根據API鉆桿規格建立有限元模型，選用101.6 mm鉆桿。

鉆桿的本體長度9.6 m，接箍外螺紋體直徑177.8 mm，內螺紋體直徑254.0 mm。由于螺紋齒形不是本研究內容，故對螺紋齒做了平滑處理，忽略具體齒形。

（3）邊界條件。鉆桿受力及約束條件為：母扣端面施加固定約束，公扣端面受到100 kN壓力、150 N·m彎曲力矩、50 N·m的扭矩。施加的載荷及約束見圖2及圖3。

圖2 母扣端面固定約束Fig.2 Fixed constraint on box face

圖3 公扣斷面受力Fig.3 Force on pin section

3.2 模型求解

Model solution

交變應力條件：疲勞模型選為恒幅加載、比例載荷的通用疲勞模型；同時設定疲勞強度因子系數為1，交變應力幅度為1，應力選為Von Mises應力。3.2.1 無缺陷鉆桿 首先對無缺陷鉆桿的應力及疲勞壽命進行求解。通過ANSYS求解得出無缺陷鉆桿的應力云圖及疲勞壽命云圖如圖4、圖5所示。

通過有限元分析計算，得到無缺陷鉆桿的平均應力為40.9 MPa，鉆桿本體的應力處于平均水平；最大應力發生在鉆桿本體與接箍間的加厚層，為89.3 MPa；最小疲勞壽命為8.169×105次，發生在鉆桿本體與接箍間的加厚層，這與該處屬于截面變化區，應力水平較高相一致。

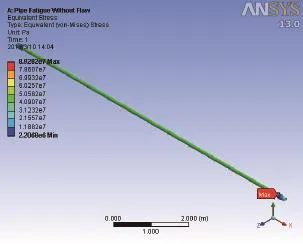
圖4 無缺陷鉆桿的應力云圖Fig.4 Stress cloud chart of defect free string

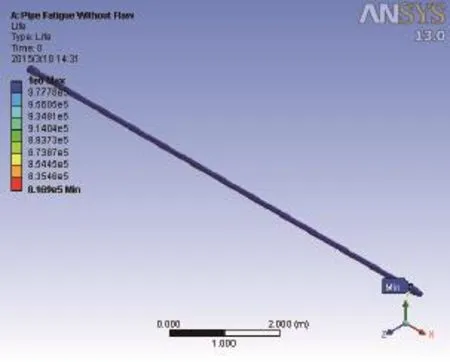
圖5 無缺陷鉆桿的疲勞壽命云圖Fig.5 Fatigue life cloud chart of defect free string

3.2.2 帶有初始缺陷的鉆桿 為研究鉆桿上初始缺陷對鉆桿疲勞壽命的影響，有限元模擬設計了不同深度、不同半長、距鉆桿接箍不同距離的缺陷的多組模擬作業。

例如，有限元分析中定義半長10 mm、深度5 mm的長橢圓柱缺陷，定位在距母扣接箍9 000 mm處。

通過有限元分析計算得，缺陷鉆桿的平均應力為44.1 MPa，比無缺陷鉆桿高7.82%；最大應力發生在鉆桿本體的缺陷處，為96.6 MPa，對比無缺陷鉆桿加厚處的89.3 MPa有8.17%的提高；缺陷鉆桿的最小疲勞壽命為5.189×105次，發生在鉆桿本體缺陷處。相對于無缺陷鉆桿8.169×105次的疲勞壽命，有著36.5%的顯著下降。缺陷鉆桿的應力云圖及疲勞壽命云圖如圖6、圖7所示。

（1）初始缺陷深度。模型中鉆桿的壁厚為8.38 mm，對缺陷深度分別為0.1、0.5、1、2、3、4、5、6、7、8、8.38（貫通）mm情況分別作了有限元模擬；裂紋半長保持10 mm不變。

缺陷深度與疲勞壽命關系如圖8所示。

由圖8可見，當初始缺陷的深度不超過2 mm時，鉆桿的疲勞壽命很高，可以看做能夠正常使用；而當初始缺陷深度進一步加大時，鉆桿的疲勞壽命迅速降低，可以視為應該退出使用，否則將會發生斷裂事故。例如，當初始缺陷的深度過大，貫通鉆桿壁厚后，鉆桿的疲勞壽命為0.533×105次，僅為無缺陷鉆桿的6.52%。

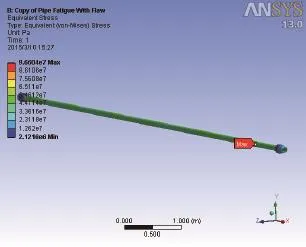
圖6 缺陷鉆桿的應力云圖Fig.6 Stress cloud chart of defective string

圖7 缺陷鉆桿的疲勞壽命云圖Fig.7 Fatigue life cloud chart of defective string

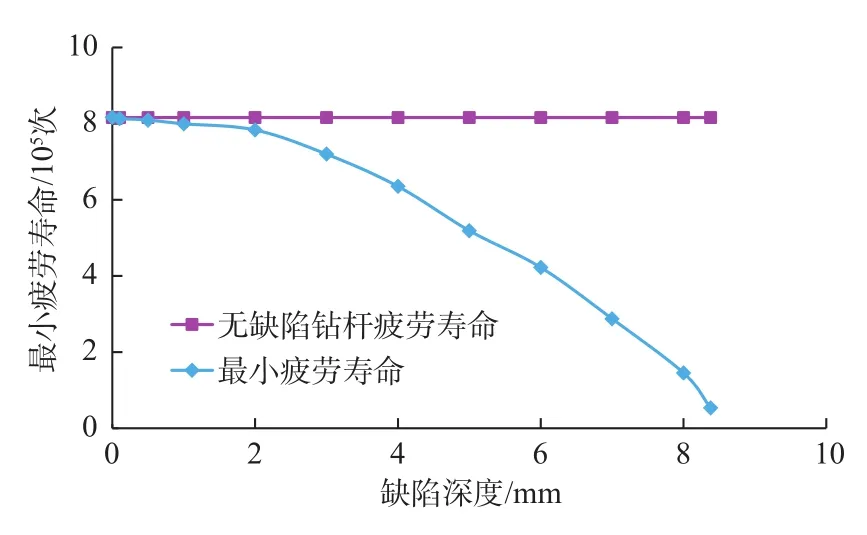
圖8 缺陷深度與疲勞壽命關系Fig.8 Relationship of imperfection depth vs.fatigue life

（2）初始缺陷半長。模型中鉆桿的外徑為101.60mm，對缺陷半長分別為1、2.5、5、7.5、10、12.5、15、17.5、20、22.5、25 mm情況分別作了有限元模擬；裂紋深度保持5 mm不變。

缺陷半長與疲勞壽命關系如圖9所示，當初始缺陷的半長不超過2.5 mm時，鉆桿的疲勞壽命很高，可以看做能夠正常使用；而當初始缺陷半長進一步加大時，鉆桿的疲勞壽命迅速降低，特別是當缺陷半長超過20 mm（接近鉆桿外徑的1/5）后，疲勞壽命降低的速度加大，可以視為應該立即退出使用，否則將會發生斷裂事故。例如，當初始缺陷的半長過大，達到22.5 mm時，鉆桿的疲勞壽命為0.809×105次，僅為無缺陷鉆桿的9.90%。

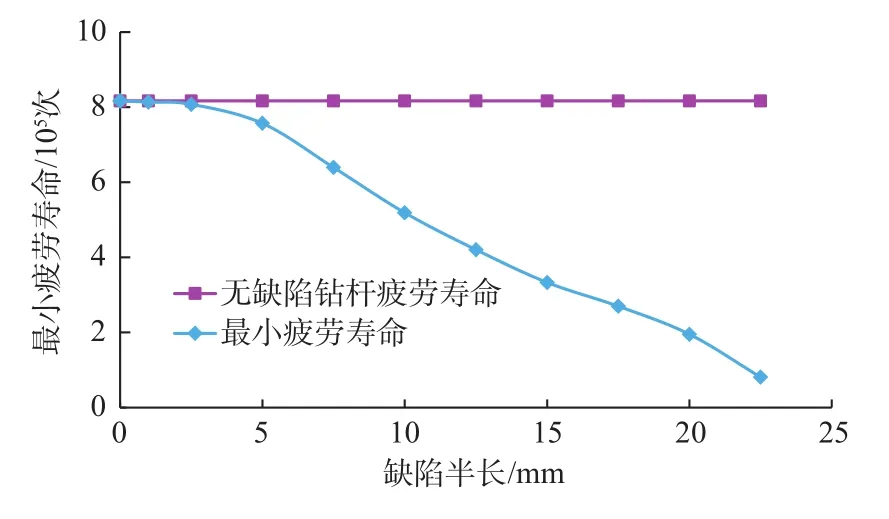
圖9 缺陷半長與疲勞壽命關系Fig.9 Relationship of imperfection semi-length vs.fatigue life

（3）初始缺陷位置。模型中鉆桿的本體長度9.6 m，接箍外螺紋體直徑177.8 mm，內螺紋體直徑254.0 mm，對缺陷距母扣接箍的距離分別為0、500、1 000、2 000、3 000、4 000、5 000、6 000、7 000、8 000、9 000、9 600（公扣處）mm情況分別作了有限元模擬；裂紋深度保持5 mm不變，半長保持10 mm不變。

缺陷位置與疲勞壽命關系如圖10所示，當缺陷的位置遠離接箍，也即在鉆桿本體中部時，疲勞壽命最大；而當缺陷越來越接近接箍，即位于接箍與本體之間的加厚區時，因該處的應力水平較高，疲勞壽命最低，約為5.2×105次；而當缺陷位于接箍上時，疲勞壽命又會略微提高，這與接箍的剛度較大有關。此外，由于母扣的厚度、剛度大于公扣，相應的，有缺陷母扣的疲勞壽命略大于有缺陷的公扣。

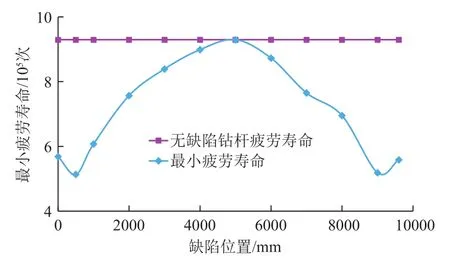
圖10 缺陷位置與疲勞壽命關系Fig.10 Relationship of imperfection location vs.fatigue life

4 結論

Conclusions

（1）井場使用中的鉆柱存在著初始缺陷，初始缺陷的存在加劇了裂紋擴展和破壞，因而需要對采用無缺陷構件假設推導的應力公式乘以應力集中系數，得出更為貼近實際的應力。

（2）鉆柱的臨界循環周次取決于初始裂紋尺寸、臨界裂紋尺寸以及裂紋的幾何形狀因子和應力強度因子；同時鉆柱的疲勞破壞來源于通過不同井段時交變狀態下鉆柱裂紋的累積和拓展，因此計算疲勞壽命時需要考慮其累積性。

（3）初始缺陷的深度和半長對鉆桿的最小疲勞壽命有著重要影響，當深度超過2 mm（大于外徑的1/4），或者半長超過2.5 mm，鉆桿的疲勞壽命迅速下降，應立即停止使用。

（4）當初始缺陷越來越接近接箍，也即位于接箍與本體之間的加厚區時，因該處的應力、應變水平較高，疲勞壽命最低，僅為本體中部的55%；鉆井實踐中，接箍與鉆桿本體的過渡區域經常受到夾持機構的咬傷，其誘發疲勞損壞的風險需加以規避。

References:

［1］李文飛，管志川，趙洪山.基于可靠性理論的鉆柱疲勞壽命預測［J］.石油鉆采工藝，2008，30（1）： 12-14.LI Wenfei,GUANZhichuan,ZHAO Hongshan.Research on fatigue life of drill string based on reliability theory［J］.Oil Drilling &Production Technology,2008,30（1）:12-14.

［2］VEIDT M,BEREZOVSKI A.Design and application of a drill pipe fatigue test facility［C］.Structural Integrity and Fracture,2004:367-373.

［3］DALEB A.An experimental investigation of fatiguecrack growth in drillstringtubulars［J］.SPE Drilling Engineering,1988,3（4）:356-362.

［4］羅增，林元華，明傳中，盧強，謝居良，劉貴喜.基于Walker模型的空氣鉆井鉆柱疲勞壽命算法［J］ .石油礦場機械，2010，39（4）：57-60.LUO Zeng,LIN Yuanhua,MING Chuanzhong,LU Qiang,XIE JuLiang,LIU Guixi.Research on predicting DWA drive drillstring fatigue life by walker model［J］.Oil Field Equipment,2010,39（4）:57-60.

［5］高寶奎，高德利.鉆柱使用壽命的不確定性分析［J］.石油鉆探技術，2003，31（5）： 63-66.GAO Baokui,GAO Deli.Analysis of nondeterminacy for drill piper service life［J］.Petroleum Drilling Techniques,2003,31（5）:63-66.

［6］杜之富.焊接圓鋼管K型節點焊縫周圍熱點應力分布規律研究［D］.煙臺：煙臺大學，2008.DU Zhifu.Research of stress distribution rule for weld cylinder steel tube about weld joint type-K ［D］.Yantai:Yantai University,2008.

［7］HOSSAINM M ,RAHMAN M K ,RAHMAN S S,AKGUN F,KINZEL H.fatigue life evaluation:a key to avoid drillpipe failure due to die-marks［R］.SPE 47789,1998.

［8］韓家強，藺剛.鉆柱受力與疲勞強度校核研究［J］.決策與信息旬刊，2014（8）：82-82.HAN Jiaqiang,LIN Gang.Research of drill string’ s stress and fatigue strength checking［J］.Decision &Information,2014（8）:82-82.

［9］楊堯焜，代成建，陳小龍，吳俊.深水鉆井鉆柱動力學機理研究［J］.科技創新導報，2015（22）：30-31.YANG Yaokun,DAI Changjian,CHEN Xiaolong,WU Jun.Mechanism research of dynamics of drill string for deep water drilling［J］.Science and Technology Innovation Herald,2015（22）:30-31.

［10］TIMOSHENKOS P,GoodierJ N.Theory of elasticity［M］.3rd rdition.New York:McGraw-Hill Book Co.Inc.,1970:250.

［11］張德平，駱發前，林元華，戴榮華，關小旭，施太和.鉆柱疲勞壽命預測研究［J］.斷塊油氣田，2006，13（3）：57-60.ZHANG Deping,LUO Faqian,LIN Yuanhua,DAI Ronghua,GUAN Xiaoxu,SHI Taihe.Research on fatigue life for drill string［J］.Fault-Block Oil &Gas Field,2006,13（3）:57-60.

（修改稿收到日期 2016-09-11）

〔編輯 薛改珍〕

Prediction method on fatigue life of string based on initial imperfection

GENG Yanan1,CHEN Xiaoliang2,YANG Jin2,LIU Shujie1,DENG He2,HE Yingming1
1.CNOOC Research Institute,Beijing 100028,China;
2.China Uniνersity of Petroleum (Beijing),Beijing 102249,China

The initial imperfection of string is one of the key factors that affect its fatigue life.In the traditional string fatigue prediction model,the effect of initial imperfection is often neglected,and consequently the predicted result is higher and the string safety is impacted.In view of the initial imperfection of strings,the extensional stress and bending stress on strings are corrected by using the stress concentration factor based on the force analysis on traditional defect-free strings.Then,the string fatigue life prediction model was built according its crack propagation laws.And finally,the average stress and minimum fatigue life of defect free strings and those with initial imperfection at different depth,semi-length and locations were simulated by means of finite element analysis tool and then compared.It is indicated that the depth and semi-length of initial imperfection have significant effect on the minimum fatigue life of strings.The closer the initial imperfection is to the collar,the more effect is has on the fatigue life of strings.The research results provide the reference for predicting the fatigue life of strings in the process of well drilling accurately so as to guarantee safe and efficient drilling.

string fatigue life;stress concentration factor;initial imperfection;finite element simulation;minimum fatigue life

耿亞楠，陳孝亮，楊進，劉書杰，鄧賀，何英明.基于初始缺陷的鉆柱疲勞壽命預測方法研究［J］.石油鉆采工藝，2016，38（6）：817-822.

TE21

A

1000-7393（ 2016 ） 06-0817-06

10.13639/j.odpt.2016.06.021

:GENG Yanan,CHEN Xiaoliang,YANG Jin,LIU Shujie,DENG He,HE Yingming.Prediction method on fatigue life of string based on initial imperfection［J］.Oil Drilling &Production Technology,2016,38(6):817-822.

攻關項目：中海油有限公司綜合科研“中海油井的完整性技術體系研究”（編號：YXKY-2015-ZY-09）；“中海油鉆完井井控技術管理體系研究”（編號：2014-YXKJ-001）。

耿亞楠（1968-），1989年畢業于中國石油大學（華東）石油工程專業，現主要從事海洋石油鉆井工程設計與研究工作。通訊地址：（100028）北京市朝陽區太陽宮南街6號院中海油大廈A704室。電話：010-84522391。E-mail:gengyn@cnooc.com.cn