玻璃纖維增強塑料錨桿粘結性能研究

匡亞川，徐 楊，歐練文

（中南大學土木工程學院，湖南長沙410075）

玻璃纖維增強塑料錨桿粘結性能研究

匡亞川，徐 楊，歐練文

（中南大學土木工程學院，湖南長沙410075）

為了研究玻璃纖維增強塑料GFRP（glass fiber reinforced plastic）錨桿的粘結性能，對GFRP錨桿軸向傳力機理進行了研究，基于Mindlin位移解，得到GFRP錨桿的剪應力和軸應力的計算公式。利用MATLAB軟件編制程序得到GFRP錨桿的剪應力及軸力沿桿體軸向方向的分布曲線。通過現場拉拔試驗結合有限元分析軟件ANSYS建模分析結果，得到了GFRP錨桿的剪應力、軸力沿桿體分布規律以及錨桿的粘結-滑移曲線，試驗值與有限分析結果及理論計算值基本吻合，驗證了有限元分析與理論推導的準確性。該研究為GFRP錨桿的設計和工程應用提供理論依據。

GFRP錨桿；傳力機理；粘結性能；現場試驗；數值分析；剪應力；軸力

錨桿在土木工程的應用非常廣泛，從1912年美國的Abershiesin第一次將錨桿用于煤礦巷道的支護中，到目前為止，經過近百年的發展，目前世界上僅各類巖石錨桿就多達數百余種，每年使用錨桿量達到2．5億根［1-2］。我國從1956年開始使用錨桿支護技術，從20世紀70年代開始，錨桿支護技術在土木工程中大量使用。但是錨桿的銹蝕已成為世界各國廣泛和長期關注的焦點。錨桿一般服役在地下水長期作用的環境中，水及其水中侵蝕性離子介質的滲透、沖刷、冰凍、侵蝕等作用使得錨桿的工作環境條件異常復雜和嚴酷，錨桿的銹蝕問題日益成為影響錨固體系安全性和耐久性的突出問題。工程上由于鋼錨桿容易銹蝕造成的損失非常巨大。國際預應力協會（FIP）曾對35個錨桿斷裂實例進行調查［3］，其中永久錨桿占69％，臨時錨桿占31％，錨桿使用期在2年內或2年以上發生腐蝕斷裂的各占一半。解決這類問題的傳統做法是在鋼材的表面噴涂防腐劑，或是改變鋼材的物理化學成分提高鋼材的耐腐蝕性［4］。但是這種做法一方面會增加錨桿安裝操作的復雜性，另一方面會提高工程的造價。采用耐腐蝕性能好的FRP（fiber reinforced plastic）新材料代替鋼材是解決錨桿腐蝕問題的重要方向。GFRP錨桿軸向抗拉強度高、抗腐蝕性能好，可解決鋼錨桿施工困難、易腐蝕等問題［5-6］。國外對GFRP粘結型錨桿研究較多［7-8］，在土層錨桿中也已有應用，而我國研究才剛剛起步，大部分的研究集中在FRP筋材的力學性能［9-12］。本文將通過理論推導，結合現場拉撥試驗及有限元分析軟件研究GFRP錨桿的粘結性能。本文的研究成果將為GFRP錨桿的設計和工程應用提供理論依據。

1 GFRP錨桿軸向傳力機理分析

GFRP錨桿的彈性模量低，表面樹脂硬度小，抗剪能力差，因此全螺紋GFRP錨桿的滑移破壞以表面肋被壓裂、削減或剪切破壞為主［13］。GFRP錨桿粘結力的分布規律可從拉拔受力過程及彈性理論解進行研究分析。

1．1 GFRP錨桿拉拔過程分析

GFRP錨桿拉拔時，假定GFRP錨桿橫截面受力均勻而且只承受拉拔力的作用。將GFRP錨桿的錨固段沿錨桿軸向方向分散為若干個微小單元，每個微小單元都與錨固體表面產生互剪作用，如圖1所示［14］。每個單元的左右兩邊受不同的拉力作用，形成拉力差，與側邊摩擦阻力平衡，可表示為

式中:d為GFRP錨桿的直徑，ΔPi為微小單元左右的拉力差，P為GFRP錨桿加載端的加載力，τ（xi）為每個微小段的側阻力。

圖1 GFRP錨桿受力示意圖Fig．1 GFRP anchor force diagram

由圖1可知，當GFRP錨桿承受拉拔荷載P時，GFRP錨桿因為拉伸變形產生了移動，這時GFRP錨桿與錨固體之間就產生了相對位移，錨固體對錨桿的剪應力τ（xi）阻止GFRP錨桿的移動。假設錨桿長度無限長時，在微小拉拔力作用下，第一個微小單元產生的摩阻力πdτ（xi）Δxi就可以平衡外荷載P的作用，隨著拉拔力P的增大，第一微小單元的摩阻力達到一定的強度πdτ（xi）Δxi仍然不能平衡外力P，則剩余的力P-πdτ（xi）Δxi將向下一個單元傳遞，下個單元的受力情況與前一個單元類似，依次傳遞，直到式（2）平衡為止。由此可見，錨桿長度較大時，GFRP錨桿的粘結力并不是沿著錨桿長度均勻分布，而是隨著荷載的增大逐漸從外向內傳播的，當荷載較大時，端口附近的一微小單元可能最先達到最大剪切強度τmax而進入塑性破壞，出現界面的脫粘現象，同時也使端口附近粘結力下降出現脫粘，而拉拔力傳遞往遠端轉移。

1．2 基于Mindlin位移解的GFRP錨桿的受力分析

考慮全長粘結式錨桿埋入巖體中，其端頭受拉拔力的情況，假定巖體與錨固體材料性質相同或錨固體材料較薄，同時假定錨固的錨桿無限長。巖體視為無限半空間，在深度h處作用集中荷載P，由Mindlin位移解可得在A（x，y，z）點處的垂直位移W［15］。假設GFRP錨桿與錨固體之間為彈性變形狀態，且錨桿孔口處，錨桿沿桿軸向伸長量與巖土體沿桿軸向位移值相等。通過微分變換，利用邊界條件，可得GFRP錨桿所受剪應力t沿桿體分布為

將式（3）兩邊積分，得到GFRP錨桿桿體軸力分布表達式:

GFRP錨桿的彈性模量Ea取值43×103MPa，直徑分別是18、25、32 mm，巖體彈性模量E取值3．05× 103MPa，泊松比v=0．25，拉拔荷載P為40 kN。利用軟件MATLAB編制程序，對式（3）和式（4）求解，可得到GFRP錨桿的剪應力及軸力沿軸向方向的分布曲線，分別如圖2和圖3所示。

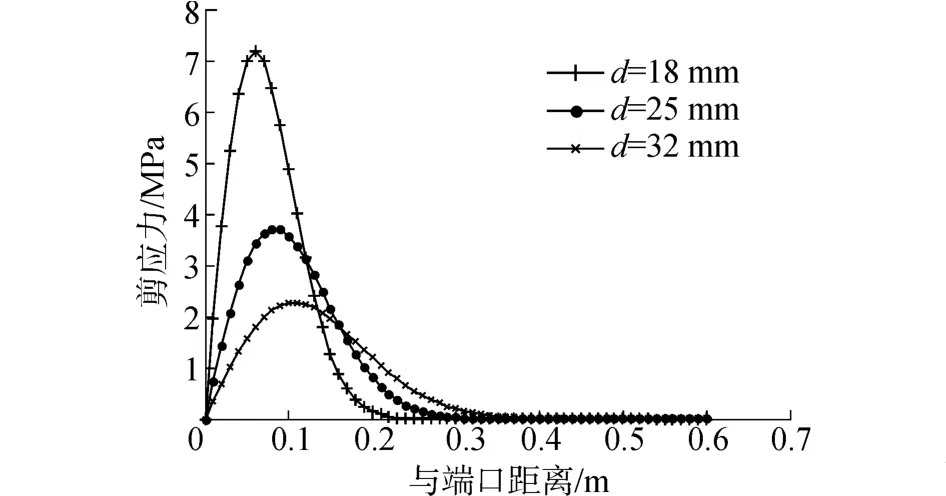
圖2 剪應力沿錨桿長度方向的分布圖Fig．2 Distribution of shear stress along the anchor length direction

從圖3可知，GFRP錨桿軸力最大值在端口，錨桿軸力從端口沿著錨桿長度方向迅速減小，并在較小的長度范圍內減小到0。而且直徑越小，軸力沿桿長度方向減小速度越快。因此，在一定條件下，增大GFRP錨桿的直徑可以減小應力集中現象。

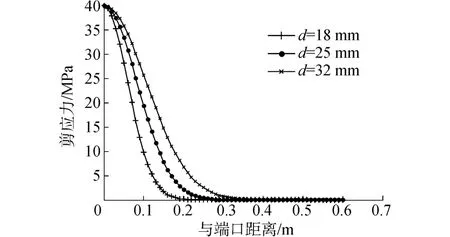
圖3 軸力沿錨桿長度方向的分布圖Fig．3 Distribution of axial force along the anchor length direction

2 GFRP錨桿現場拉拔試驗

現場拉撥試驗在湖南省懷化市托口水電站大壩進行，如圖4所示。錨固體為灰白色的石灰巖，彈性模量E取值32．5×103MPa，泊松比v=0．35，粘聚力為2 MPa，內摩擦角為30°，密度為2．5 g／cm3，軟化系數0．8，空隙率為30，吸水率為2．4，抗壓強度為125 MPa。GFRP錨桿直徑為18 mm和25 mm，采用水灰比0．5的純水泥漿進行注漿，水泥為42．5級普通硅酸鹽水泥

圖4 托口水電站大壩Fig．4 Tuokou hydropower dam

2．1 拉撥試驗

試驗前在錨桿上沿長度方向粘貼應變片，應變片對稱分布，如圖5所示。然后，鉆孔、清孔、安裝錨桿、灌注砂漿。養護到齡期后，采用拉拔儀（如圖6所示）進行拉拔試驗。

圖5 GFRP錨桿應變片布置圖Fig．5 Layout of GFRP bolt strain gauge

圖6 拉拔試驗裝置Fig．6 Set-up of pull-out test

試驗時采用分級加載，每級荷載施加完成后，穩定10 min，記錄數據，再進行下一級加載試驗。在拉撥試驗進行時，同時采用千分表測量錨桿桿端的滑移，如圖7所示。

圖7 錨桿桿端滑移測量Fig．7 The anchor rod end slip measurement

2．2 試驗結果與分析

2．2．1 試驗結果

GFRP錨桿在荷載作用下桿體的應變值如表1、2所示。

表1 Φ25 GFRP錨桿荷載作用下桿體的應變值（×10-6）Table 1 Φ25 GFRP anchors train value under loads

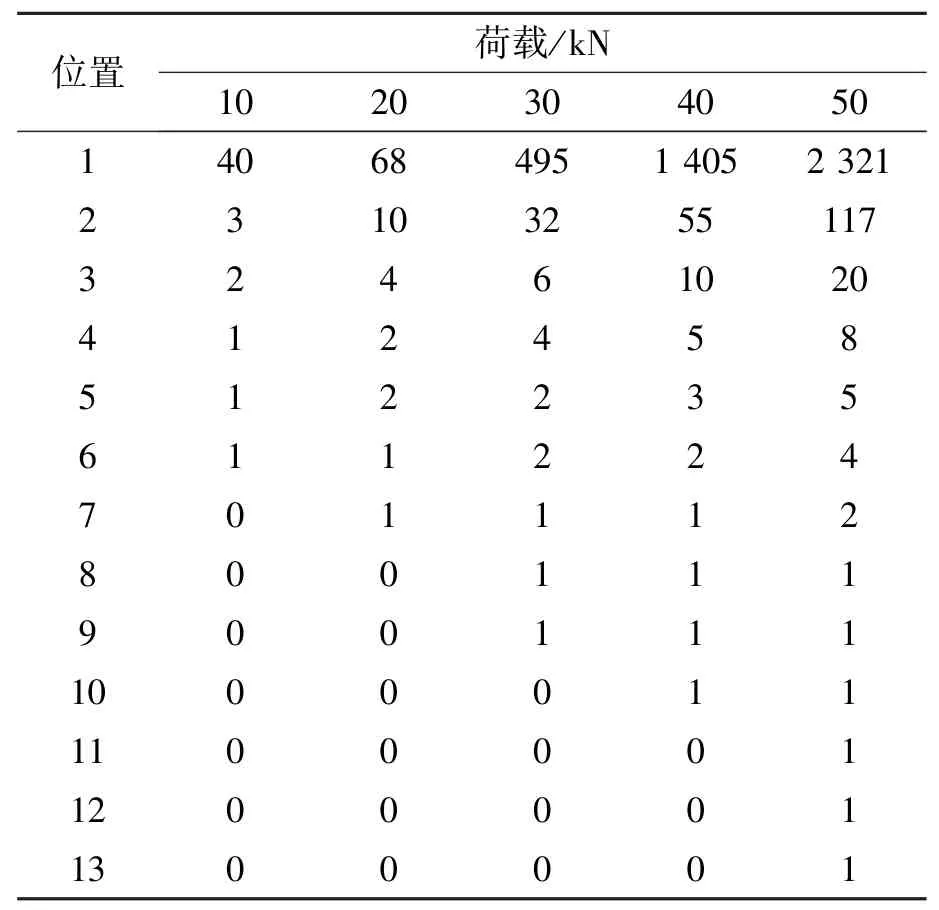
表2 Φ18 GFRP錨桿在荷載作用下的的應變值（×10-6）Table 2 Φ18 GFRP anchor strain value under loads

試驗時隨著荷載的增大，端口逐漸產生微裂縫，并向四周擴展，桿體出現滑移。錨桿在不同荷載作用下的滑移值如表3、4所示。

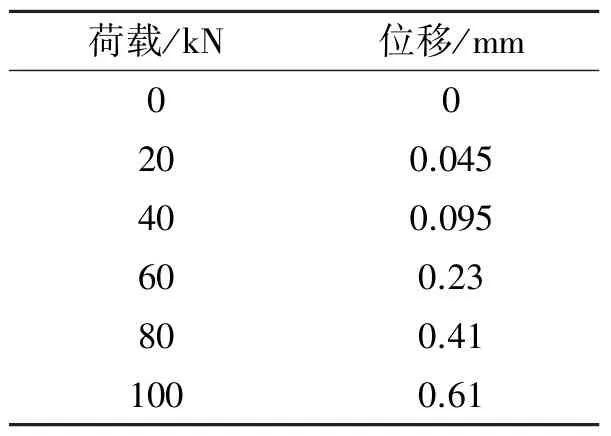
表3 Φ25 GFRP錨桿在荷載作用下的滑移值Table 3 Φ25 GFRP anchor slip value under loads

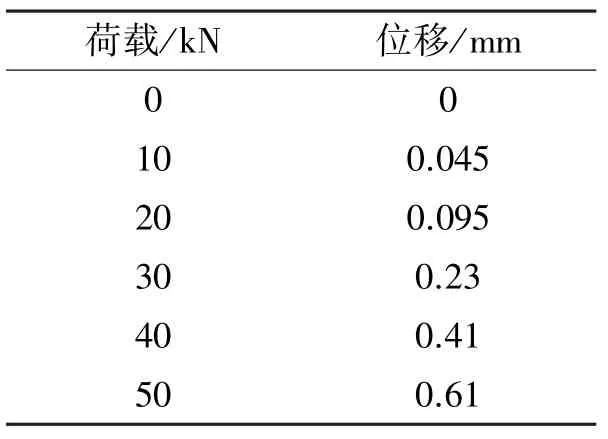
表4 Φ18 GFRP錨桿在荷載作用下的滑移值Table 4 Φ18 GFRP anchor slip value under loads

2．2．2 剪應力沿桿體分布規律

GFRP錨固的粘結應力在相鄰兩個測點之間可假定為均勻分布，根據力的平衡條件，即

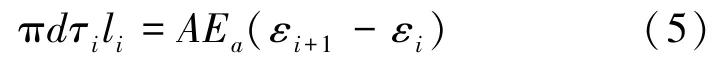
式中:εi+1、εi分別為i+1點和i點測得的應變，d為GFRP錨桿的直徑，Ea為GFRP錨桿的彈性模量，A為GFRP錨桿的橫截面積，li為GFRP錨桿第i點到第i+1點的距離。

在加載端口的剪應力為0，則根據式（5）可以得到GFRP錨桿的剪應力沿錨桿長度方向分布的規律，如圖8、9所示。

圖8 Φ25 GFRP錨桿的剪應力沿桿體分布規律Fig．8 Shear stress distribution along the rod body of Φ25 GFRP anchor

圖9 Φ18 GFRP錨桿的剪應力沿桿體的分布規律Fig．9 Shear stress distribution along the rod body of Φ18 GFRP anchor

由圖8和圖9可知，GFRP錨桿的剪應力，沿著錨桿長度方向是不均勻的，在端口附近達到最大值，然后沿著錨桿長度方向急劇降低，最終趨于0，錨固影響范圍較小。隨著拉拔力的增大，峰值剪應力增大，同時剪應力的分布范圍有所增大，但增大效果并不顯著。錨桿直徑增大，峰值剪應力減小，但剪應力分布范圍增大。

圖10為40 kN荷載作用下，直徑為25 mm的GFRP錨桿的剪應力試驗值與Mindlin公式計算結果對比圖，從圖10中可以看出試驗值與Mindlin公式計算值比較接近。Mindlin理論計算得到的峰值剪應力略大于試驗所得值，這主要是由于理論計算是在彈性理想條件下，而且并不考慮錨固劑與巖土體之間的作用以及巖土體的塑性作用，因此應力集中現象較嚴重，計算所得峰值剪應力略偏大。

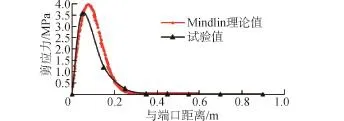
圖10 P=40 kN時錨桿的剪應力理論值與試驗值Fig．10 P=40 kN shear stress theoretical values and test values of anchors

2．2．3 軸力沿桿體分布規律

GFRP錨桿為線性材料，由表1、2的應變值可計算得到GFRP錨桿桿體軸力分布，如圖11、12所示。

由圖11、12可知，GFRP錨桿的軸向力在端口處最大，為實際施加的試驗拉拔力，從端口沿著錨桿長度方向逐漸減小，并在較小的長度范圍內就減小到0。隨著荷載的增大，錨桿的端口軸力也增大，錨固影響范圍有所增大，但并不明顯。相同荷載（20 kN，40 kN）作用下，Φ25的GFRP錨桿軸力傳遞范圍比Φ18錨桿的傳遞范圍要大一些，這是由于直徑越大，表面缺陷越多，粘結應力就較小，這樣就需要更大的錨固范圍來平衡拉拔力。

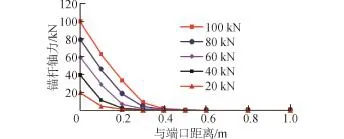
圖11 Φ25 GFRP錨桿軸力沿桿體的分布規律Fig．11 Axial force distribution along the rod body of Φ25 GFRP anchor

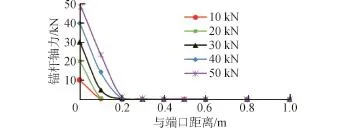
圖12 Φ18 GFRP錨桿軸力沿桿體的分布規律Fig．12 Axial force distribution along the rod body of Φ18 GFRP anchor

圖13為40 kN荷載作用下，直徑25 mm的GFRP錨桿的軸力沿桿體分布的試驗值與Mindlin公式計算值對比圖，試驗值與Mindlin公式值比較接近。

圖13 P=40 kN時錨桿軸力的理論值與試驗值Fig．13 P=40 kN axial force theoretical values and test values of anchors

2．2．4 粘結-滑移曲線

由表3、4滑移值可得到GFRP錨桿的粘結-滑移曲線關系，如圖14所示。

從圖14可知，GFRP錨桿的粘結-滑移曲線可分為兩部分:微滑移段和滑移段，在微滑移段，化學膠著力起主要作用，粘結應力隨荷載增大而成線性增大，但滑移量較小。隨著荷載的增大，化學膠著力所起作用越來越小，摩擦力與機械咬合力起主要作用，粘結應力隨荷載增大的幅度降低，而滑移量增大幅度較大，進入了滑移段。錨桿直徑增大，粘結應力降低，而滑移量卻在增大。GFRP錨桿的直徑越大，錨固體的泌水現象越嚴重，界面空隙及缺陷越大，粘結強度降低；同時GFRP錨桿表面包裹的樹脂剪切剛度較小，與中心區域的纖維變形不同時，造成剪切滯后現象，直徑越大，這種滯后現象越嚴重，粘結應力就越低。

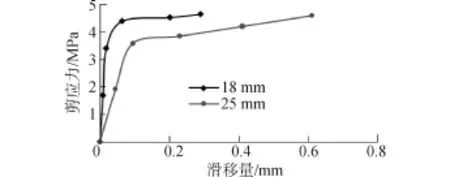
圖14 不同直徑的GFRP錨桿的粘結-滑移曲線Fig．14 Bond-slip relationship curve of GFRP anchor with different diameters

3 基于ANSYS彈簧單元的GFRP錨桿粘結性能有限元分析

3．1 有限元模型的建立與求解

3．1．1 模型建立

考慮GFRP錨桿與巖土體之間的粘結-滑移性能，建模時在GFRP錨桿與巖土體之間引入Combination39彈簧單元。GFRP錨桿選用LINK8單元。巖土體單元選用SOLID45單元，巖土體材料采用DP材料。GFRP錨桿的直徑分別為18 mm和25 mm，巖土的計算模型取外徑為1 000 mm進行有限元分析。有限元模型如圖15所示。

圖15 有限元模型Fig．15 The finite element model

3．1．2 約束邊界條件和施加荷載

由于巖土體的直徑遠大于30倍的GFRP錨桿直徑，因此在巖土體四周的邊界條件不再受外力的影響，在y=0的底面上施加x、y、z三個方向的面約束。根據試驗加載情況，在GFRP錨桿單元的頂點施加一個沿軸向方向的集中荷載，進行求解分析。

3．2 ANSYS計算結果及分析

在荷載作用下GFRP錨桿剪應力、軸應力沿桿體的分布規律如圖16、17所示。

從圖16和圖17中可以看出，軸力沿錨固長度方向逐漸減小，粘結應力在端口附近達到峰值，然后逐漸減小到0，錨固粘結范圍較小。

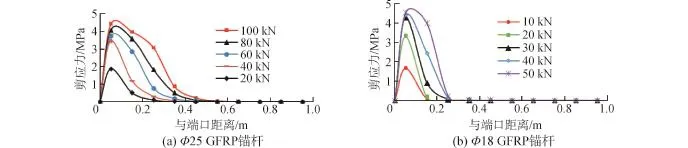
圖16 荷載作用下錨桿剪應力沿錨桿長度方向分布Fig．16 Distribution of shear stress along the anchor length direction under the load

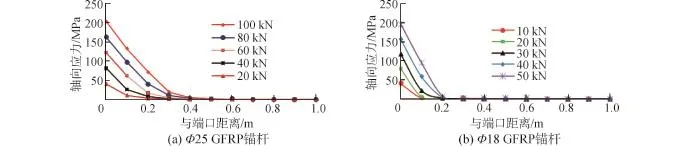
圖17 荷載作用下軸向應力沿錨桿長度方向分布Fig．17 Distribution of axial stress along the anchor length direction under the load

圖18、19為40 kN荷載作用下，直徑為25 mm的GFRP錨桿的剪應力及軸力理論計算值、試驗值以及ANSYS分析值的對比圖。可以看出，錨桿的剪應力及軸力的ANSYS有限元分析值與Mindlin計算結果以及試驗結果基本一致。

圖18 剪應力的理論值、試驗值及模擬值Fig．18 The theoretical value，experimental value and simulation value of shear stress

圖19 軸力的理論值、試驗值及模擬值Fig．19 The theoretical value，experimental value and simulation value of axial force

圖20為在荷載作用下GFRP錨桿滑移沿桿體的分布規律。圖21為荷載作用下GFRP錨桿滑移量的ANSYS分析值、理論計算值以及試驗值的對比圖。

從圖21可以發現ANSYS有限元分析的粘結-滑移曲線走勢與試驗結果基本一致。

圖20 荷載作用下錨桿位移沿錨桿長度方向分布Fig．20 The distribution of anchor displacement along the anchor length directionunder the load

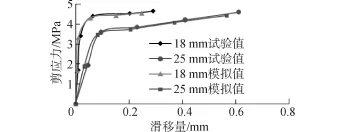
圖21 GFRP錨桿的粘結-滑移理論值與試驗值Fig．21 Theoretical value and test value of the bond-slip of GFRP anchor

4 結論

通過理論分析、現場試驗以及數值模擬分析，研究了GFRP錨桿的粘結性能，得到了以下主要結論:

1）研究了GFRP錨桿的傳力過程，利用MATLAB軟件編制程序得到得到GFRP錨桿的剪應力及軸力沿桿體軸向方向的分布曲線。

2）GFRP錨桿的剪應力，沿著錨桿長度方向是不均勻的，剪應力在錨桿端口為0，而在端口附近迅速達到最大值，然后沿著錨桿長度方向急劇降低，最終趨于0，錨固影響范圍較小；隨著拉拔力的增大，峰值剪應力增大，剪應力的分布范圍有所增大。直徑增大，峰值剪應力減小，但剪應力分布范圍增大。

3）GFRP錨桿的軸向力在端口處最大，為實際施加的試驗拉拔力，從端口沿著錨桿長度方向迅速減小，并在較小的長度范圍內就減小到0。隨著荷載的增大，錨桿的端口軸力也增大，錨固影響范圍有所增大。

4）GFRP錨桿的粘結-滑移曲線可分為微滑移段和滑移段兩部分。錨桿直徑增大，粘結應力降低，而滑移量增加。

5）試驗值與ANSYS分析值，理論計算值基本吻合，可為GFRP錨桿的設計和工程應用提供理論依據。

［1］張樂文，汪稔．巖土錨固理論研究之現狀［J］．巖土力學，2002，23（5）:627-631．ZHANG Lewen，WANG Ren．Research on status quo of anchorage theory of rock and soil［J］．Rock and soil mechanics，2002，23（5）:627-631．

［2］程良奎，李象范．巖土錨固·土釘·噴射混凝土—原理、設計與應用［M］．北京:中國建筑工業出版社，2008．CHENG Liangkui，LI Xiangfan．Geotechnical anchoring，soil nail，shotcreting-principles，design and application［M］．Beijing:China Architecture and Building Press，2008．

［3］中國工程建設標準化協會．CECS 22-2005，巖土錨桿（索）技術規程［S］．北京:中國計劃出版社，2005．China Engineering Construction Standardization Association． CECS 22-2005，Technical specification for ground anchors［S］．Beijing:China Planning Press，2005．

［4］NGUYEN T，MARTIN J W．Modes and mechanisms for the degradation of fusion-bonded epoxy-coated steel in a marine concrete environment［J］．JCT research，2004，1（2）:81-92．

［5］AHMED E A，EL-SALAKAWY E F，BENMOKRANE B．Tensile capacity of GFRP postinstalled adhesive anchors in concrete［J］．Journal of composites for construction，2008，12（6）:596-607．

［6］American Concrete Institute．Guide for the design and construction of concrete reinforced with FRP bars，ACI 440．1R-03［R］．Farmington Hills:American Concrete Institute，2006．

［7］ARIAS J P M，VAZQUEZ A，ESCOBAR M M．Use of sand coating to improve bonding between GFRP bars and concrete［J］．Journal of composite materials，2012，46（18）:2271-2278．

［8］BERTHET J F，FERRIER E，HAMELIN P，et al．Modelling of the creep behavior of FRP-confined short concrete columns under compressive loading［J］．Materials and structures，2006，39（1）:53-62．

［9］劉漢東，高磊，李國維．GFRP錨桿錨固機理試驗研究［J］．華北水利水電學院學報，2007，28（3）:63-65．LIU Handong，GAO Lei，LI Guowei．Experimental study on anchoring mechanism of GFRP bolt［J］．Journal of North China Institute of Water Conservancy and Hydroelectric Power，2007，28（3）:63-65．

［10］李偉偉，張明義，白曉宇．GFRP抗浮錨桿外錨固試驗研究及數值模擬［J］．工程建設，2013，45（6）:7-10．LI Weiwei，ZHANG Mingyi，BAI Xiaoyu．Test study and numerical simulation of external anchorage of GFRP anti-floating anchor［J］．Engineering construction，2013，45（6）:7-10．

［11］劉穎浩，袁勇．全螺紋GFRP黏結型錨桿錨固性能試驗研究［J］．巖石力學與工程學報，2010，29（2）:394-400．LIU Yinghao，YUAN Yong．Experimental research on anchorage performance of full-thread GFRP bonding anchor bolts［J］．Chinese journal of rock mechanics and engineering，2010，29（2）:394-400．

［12］鄭祖嘉．GFRP筋粘結性能與作用機理研究［D］．武漢:武漢科技大學，2015．ZHENG Zujia．Research on bond behavior and mechanism of GFRP bars［D］．Wuhan:Wuhan University of Science and Technology，2015．

［13］高磊．GFRP錨桿抗拉拔特征及破壞機理試驗研究［D］．鄭州:華北水利水電學院，2007．GAO Lei．Experimental study on tensile character and failure mechanism of GFRP rebar［D］．Zhengzhou:North China University of Water Resources and Electric Power，2007．

［14］白金超．巖土錨固的FBG-FRP錨桿及其智能監測系統［D］．哈爾濱:哈爾濱工業大學，2008:25-27．BAI Jinchao．FBG-FRP anchor bolts and intelligent monitoring systems of ground anchorage［D］．Harbin:Harbin Institute of Technology，2008:25-27．

［15］尤春安．全長粘結式錨桿的受力分析［J］．巖石力學與工程學報，2000，19（3）:339-341．YOU Chun′an．Mechanical analysis on wholly grouted anchor［J］．Chinese journal of rock mechanics and engineering，2000，19（3）:339-341．

Research on the bond behavior of a glass-fiber-reinforced plastic bolt

KUANG Yachuan，XU Yang，OU Lianwen
（School of Civil Engineering，Central South University，Changsha 410075，China）

To study the bonding performance of a glass-fiber-reinforced plastic（GFRP）bolt，its force transmission mechanism is analyzed．Moreover，based on the Mindlin solution，a formula for the calculation of shear stress and axial stress is proposed．The distribution curves of the shear stress and axial force along the axial direction of the GFRP bolt were obtained using MATLAB．The distribution laws of shear stress and axial force of the GFRP bolt and the bond slip curve were obtained by pull-out tests and finite element analysis using ANSYS software．The experimental results are consistent with the finite element analysis results and the theoretical calculation results，and the accuracy of the finite element analysis and the theoretical derivation is verified．Thus，a theoretical basis for the design and engineering application of GFRP bolts is provided．

GFRP bolt；force transmission mechanism；bond performance；field test；numerical analysis；shear stress；axial force

10．11990／jheu．201510036

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．032．html

TU45

A

1006-7043（2016）12-1658-07

匡亞川，徐楊，歐練文．玻璃纖維增強塑料錨桿粘結性能研究［J］．哈爾濱工程大學學報，2016，37（12）:1658-1664．

2015-10-16．

2016-09-28．

國家自然科學基金項目（51008314）；長江學者和創新團隊發展計劃資助項目（IRT1296）．

匡亞川（1975-），男，副教授．

匡亞川，E-mail:Kuangyachuan＠csu．edu．cn．

KUANG Yachuan，XU Yang，OU Lianwen．Research on the bond behavior of a glass-fiber-reinforced plastic bolt［J］．Journal of Harbin Engineering University，2016，37（12）:1658-1664．