多重狀態時滯系統的min-max魯棒預測控制

周衛東，鄭 蘭，廖成毅，蔡佳楠

（1．哈爾濱工程大學自動化學院，黑龍江哈爾濱150001；2．中國船舶及海洋工程設計研究院，上海200011；3．中國電子科技集團公司第三十八研究所，安徽合肥230088）

多重狀態時滯系統的min-max魯棒預測控制

周衛東1，鄭 蘭1，廖成毅2，蔡佳楠3

（1．哈爾濱工程大學自動化學院，黑龍江哈爾濱150001；2．中國船舶及海洋工程設計研究院，上海200011；3．中國電子科技集團公司第三十八研究所，安徽合肥230088）

針對一類帶有擾動、多重狀態時滯的凸多面體不確定離散非線性系統，基于預測控制理論提出一種minmax魯棒預測控制算法。將模型預測控制問題描述為一類無限時域min-max優化問題；采用LMI技術把此問題轉變為一類采用LMI描述的約束問題，設計了狀態反饋控制器；運用所給信息構造一個改進的Lyapunov-Krasovskii泛函，根據模型預測控制基本原理來求解此優化問題，同時給出了控制器存在的定理及相關證明，進而獲得所設計控制器存在的新判據及狀態反饋矩陣構造方法，在此基礎上給出了魯棒模型預測控制算法流程。最后，給出了閉環系統漸進魯棒穩定定理，理論及仿真分析驗證了控制器設計的可行性及系統的魯棒漸近穩定性。

非線性擾動；多重狀態時滯；離散非線性系統；狀態反饋控制；模型預測控制；線性矩陣不等式

模型預測控制（model predictive controlMPC）具有模型預測、滾動優化和反饋校正三個主要特性。對模型要求低、設計簡單、魯棒性強而且能夠有效的處理狀態、控制等方面的約束問題，在工業界受到廣泛的關注［1］。

在實際生產過程中不確定性與擾動是不可避免且無法預知的，而魯棒預測控制因其既具備魯棒控制的優點，可以處理模型的不確定性，又兼具預測控制的滾動優化思想，彌補了經典MPC的不足，因此得到學者們的極大重視［2-8］。文獻［2］基于LMI方法給出了一類具有時變時滯、輸入約束和擾動的離散系統的控制器設計方法；文獻［3］解決了前提不匹配情況下T-S模糊時滯系統的控制器設計問題，該文降低了設計的保守性；文獻［4-5］針對具有輸入約束的離散時滯系統通過LMI技術研究了一種魯棒模型預測控制器設計方法，但是在時滯為常數時研究的；文獻［6］采用魯棒預測控制方法研究了一類帶有非線性擾動的多重時滯不確定系統的控制律設計問題，但所考慮的系統為連續的；文獻［7］解決了一類帶有區間時滯的離散非線性系統的預測控制器設計問題；文獻［8］研究了一類時滯為多重的不確定離散線性系統的控制器設計方法，所提方法保證了閉環系統的穩定性與可行性。然而，有關多重狀態時滯與擾動同時存在的不確定離散非線性系統的魯棒預測控制問題還有待進一步研究。本文在文獻［7-8］的基礎上，討論了一類既具有非線性擾動又同時存在多重狀態時滯的不確定離散非線性系統的魯棒預測控制器設計問題。

1 問題描述與預備知識

記號:Rn為n維歐幾里德空間，Rn×m為n×m維實矩陣的集合，In為n×n維單位矩陣。符號?代表相應的對稱塊矩陣，即如果H，R是對稱矩陣，則

考慮如下一類具有多重狀態時滯和非線性擾動的不確定離散非線性系統:

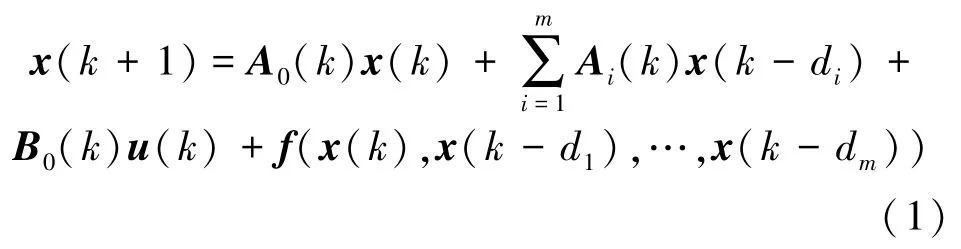
式中:x（k）∈Rnx是系統的狀態，u（k）∈Rnu為系統的輸入，f（x（k），x（k-d1），…，x（k-dm））是非線性擾動，為方便表述，令fk:=f（x（k），x（k-d1），…，x（k-dm）），且滿足:

式中:0＜d1＜…＜dm表示系統的時滯，x（k）= φ（k），-dm≤k≤0是系統的初始條件。系統（1）中的系統矩陣是未知的，并且可以表示成凸組合的形式，即

其中

式中:Co表示由L個頂點［A01A11…Am1B01］，…，［A0LA1L…AmLB0L］構成的凸多面體集，即存在L個非負系數0≤λi（k）≤1（i=1，2，…，L），使得

系統（1）的模型預測控制問題可描述為如下問題:設計一種魯棒預測控制器使所研究系統魯棒穩定同時獲得下面的魯棒性能指標，即需要考慮如下min-max優化問題:

式中:Q1＞0為性能指標中狀態的對稱加權矩陣，R＞0為控制的對稱加權矩陣表示k時刻對k+j時刻輸入的預測表示k時刻對k+j時刻狀態的預測，并且有

式（6）表示未來控制輸入的無限時域和系統預測狀態的二次魯棒性能指標，式（7）表示系統的狀態預測模型。

針對系統（1），設計如下的狀態反饋控制律:

控制目標:求取所設計控制器中的增益矩陣K，并要求控制輸入使得閉環系統漸進穩定。

針對系統（1），構造如下的Lyapunov-Krasovskii函數:

假設在每一個k≥d1時刻是可測量的。在k時刻，假設對所有的［A0（k） A1（k）…Am（k） B（k）］∈Ω，i≥0，有下式成立:

其中

為了使J∞(k)有界，令因此將不等式（10）兩邊同時從j=0到 j=∞求和，可得

因此:

根據本文所需先給出下面的兩個引理。

引理1［9］（Schur補）矩陣不等式:

式中:Q( x)=QT(x)，R( x)=RT(x)，S( x)是關于x的仿射函數，則式（13）等價于:1）Q( x)＞0，R( x)-ST(x)Q-1(x)S( x)＞0；2）R( x)＞0，Q( x)-S( x)R-1(x)ST(x)＞0。

引理2［10］設W0(x)和W1(x)都是關于x∈Rn的二次函數，如果對任意的x∈Rn-{0}，有W1(x)＜0，并且存在常數ρ＞0使得

W0(x)-ρW1(x)＜0， x≠0（14）

成立，則有W0(x)＜0。

2 控制器設計及穩定性分析

2．1 基于LMI的模型預測控制器設計

定理1考慮含有延時的離散不確定時滯系統（1），同時令為采樣k時刻狀態x（k）的測量值。如果存在標量γ（k）＞0，ρ＞0，對稱的正定矩陣Q，Qdi，P0，Pd1，…，Pdm和適當維數的矩陣Y滿足下述形式的LMI優化問題，那么一定存在狀態反饋控制律u滿足性能目標（10），其中狀態反饋增益K=YQ-1。

其中

證明:由于式（9）是性能指標的上界，可以通過求解下面的問題把這個界減至最低:

其中，

應用Schur補，式（18）可寫為

將式（19）分別左乘和右乘矩陣diag( I，P)，則有

則不等式（16）成立。下面將證明不等式（17）成立。

取Lyapunov-Krasovskii函數（9），對它求差分有

則

其中

通過計算:

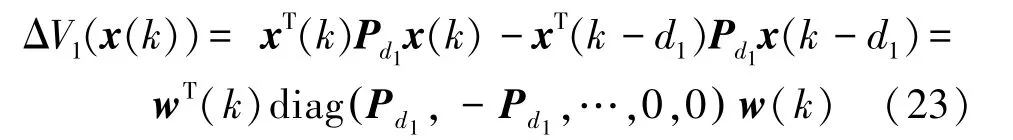
進一步:

把式（22）～（24）代入到式（21），有

其中

考慮式（10）和u（k）=Kx（k），設

其中，Θ2=diag( Pd1-P0+Q1+KTRK，-Pd1，…，-Pdm，0)又因為式（2）可以寫成:

其中

根據引理2，存在數λ＞0使得W0(x)-λW1(x)＜0成立，則W0(x)＜0，即

其中

再利用Schur補有

其中

又因為式關于系統矩陣滿足［A0（k） A1（k）…Am（k） B（k）］∈Ω，根據凸集的基本性質，式（31）成立當且僅當對凸包Ω的每個頂點都成立，即式（31）成立當且僅當式（17）成立。

2．2 控制算法

綜合上面的控制器設計過程，系統（1）的控制算法如下:

1）測量當前時刻系統的狀態x（k），并獲得過去時刻的狀態x（k-1），…，x（k-d1），…，x（k-dm）；

3）選擇適當的對稱正定矩陣Q1和R；

4）定義優化問題（5）～（7）中的各個變量，標量γ（k）＞0，ρ＞0，正定對稱矩陣Q，Qdi，P，Pd1，…，Pdm和適當維數的矩陣Y；

5）用MATLAB中的LMI工具箱求解優化問題（5）～（7），得到最優解γ（k），ρ，Y，Q，Qdi，P0，Pd1，…，Pdm；

6）計算出狀態反饋預測控制控制器增益矩陣K=YQ-1；

8）令k=k+1，重復步驟1）～7）。

2．3 可行性與穩定性分析

引理3［11］（可行性） 如果定理1中該優化問題在k時刻是可行的，那么它對所有k+j，j＞0都是可行的。

定理2如果優化問題（5）～（7）在k時刻是可行的，則由定理1給出的狀態反饋控制器u（k）= Kx（k）使閉環系統魯棒漸近穩定。

證明由引理3可知最優化問題（5）～（7）是可行的。所以假設分別表示最優化問題（5）～（7）在k時刻和k+1時刻的最優解，最優狀態分別為和

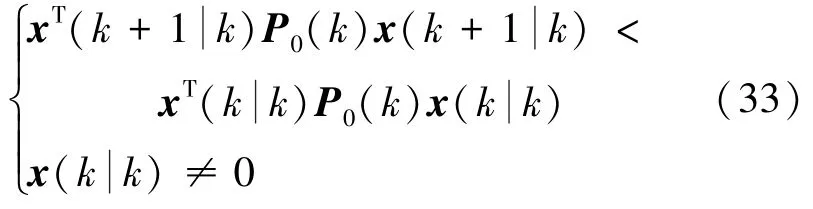
由上述假設可知:

這里i=1，2，…，d1，…，dm。則有

又因為測量狀態

式（35）說明V( k｜k)是單調非增且有界的Lyapunov函數，當k→∞時，有x( k)→0。由離散Lyapunov穩定性理論可以說明閉環系統魯棒穩定。

3 仿真結果與分析

考慮如下帶有非線性擾動、時滯和凸多面體不確定的離散非線性系統:

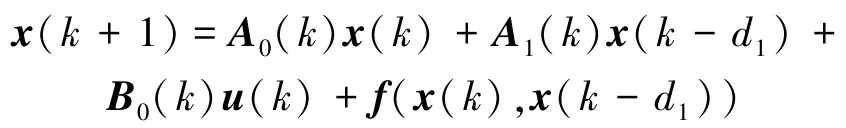
其中

圖1 狀態x1(k)的時間響應曲線Fig．1 Time response of the state x1(k)

圖3是控制器曲線圖，可以看出在該控制器的作用下，系統是穩定的而且性能也很好。

4 結論

1）基于LMI技術及變量變換思想提出了一種min-max魯棒預測控制算法，將時域為無限時的最小、最大優化問題轉換為一類凸優化問題。解決了一類同時帶有多重狀態時滯、擾動和多面體不確定離散非線性系統的控制器設計問題。

2）算法通過利用所構造的改進的二次Lyapunov-Krasovskii泛函得到了所設計的控制器存在的新判據。應用LMI技術得到的魯棒預測控制器，保證了系統的魯棒穩定性，并分析了控制算法的可行性。

3）最后的仿真結果表明了該方法的有效可行。

［1］何德峰，丁寶蒼，于樹友．非線性系統模型預測控制若干基本特點與主題回顧［J］．控制理論與應用，2013，30（3）:273-287．HE Defeng，DING Baocang，YU Shuyou．Review of fundamental properties and topics of model predictive control for nonlinear systems［J］．Control theory＆applications，2013，30（3）:273-287．

［2］趙杰梅，胡忠輝，張利軍．區間時滯相關離散非線性系統的魯棒模型預測控制［J］．控制與決策，2015，30（1）: 59-64．ZHAO Jiemei，HU Zhonghui，ZHANG Lijun．Robust model predictive control for discrete-time nonlinear systems with delay-range-dependent［J］．Control and decision，2015，30（1）:59-64．

［3］俞華軍．帶有非線性擾動的不確定時滯系統魯棒預測控制［J］．電子設計工程，2016，24（6）:190-193．YU Huajun．Robust predictive control of uncertain time-delay systems with nonlinear disturbance［J］．Electronic design engineering，2016，24（6）:190-193．

［4］CHEN Qiuxia，HE Defeng，YU Li．Input-to-state stability of min-max MPC scheme for nonlinear time-varying delay systems［J］．Asian journal of control，2012，14（2）:489-501．

［5］SHI Yujing，CHAI Tianyou，WANG Hong，et al．Delay-dependent robust model predictive control for time-delay systems with input constraints［C］／／Proceedings of the 2009 conference on American Control Conference．Piscataway，NJ，USA:ACM，2009:4880-4885．

［6］蘇成利，趙家程，李平．一類具有非線性擾動的多重時滯不確定系統魯棒預測控制［J］．自動化學報，2013，39（5）:644-649．SU Chengli，ZHAO Jiacheng，LI Ping．Robust predictive control for a class of multiple time delay uncertain systems with nonlinear disturbance［J］．Acta automatica sinica，2013，39（5）:644-649．

［7］LI Jianxiong，FANG Yiming，SHI Shengli．Robust MPC algorithm for discrete-time systems with time-varying delay and nonlinear perturbations［C］／／Proceedings of the 29th Chinese Control Conference．Beijing，China:China Automation Society Control Theory Specialized Committee，2010:3128-3133．

［8］ZHAO Juncheng，FANG Yiming，LI Jianxiong．Robust predictive control for a class of uncertain discrete system with multiple state delays［C］／／Proceedings of the 30th Chinese Control Conference．Yantai，China:IEEE，2011:3372-3376．

［9］俞立．魯棒控制:線性矩陣不等式處理方法［M］．北京:清華大學出版社，2002．

［10］馬新軍，向少華，胥布工，等．帶非線性擾動的不確定多時變時滯系統H∞魯棒穩定性［J］．控制理論與應用，2006，23（4）:631-635．MA Xinjun，XIANG Shaohua，XU Bugong，et al．H-infinity robust stability for uncertain systems with multiple timevarying delays and nonlinear perturbations［J］．Control theory＆applications，2006，23（4）:631-635．

［11］KOTHARE M V，BALAKRISHNAN V，MORARI M．Robust constrained model predictive control using linear matrix inequalities［J］．Automatica，1996，32（10）:1361-1379．

Min-max robust predictive control for multi-state time-delay systems

ZHOU Weidong1，ZHENG Lan1，LIAO Chengyi2，CAI Jianan3
（1．College of Automation，Harbin Engineering University，Harbin 150001，China；2．Marine Design and Research Institute of China，Shanghai 200011，China；3．China Electronics Technology Group Corporation No．38 Research Institute，Hefei 230088，China）

For a class of convex polyhedron uncertain discrete nonlinear systems with disturbance and multi-state time delays，a min-max robust predictive control algorithm is proposed based on the predictive control theorem．Firstly，the model prediction control problem is described as a class of min-max problems for an infinite time-domain．Then，using liner matrix inequalitie（LMI）technology，the problem is transformed into a constraint problem and a state feedback controller designed．An improved Lyapunov-Krasovskii function is constructed using information provided，and the optimization problem is solved based on model predictive control theory．At the same time，the theorem and its proofs for the existence of the designed controller are also given．Thus，new evidence for the existence of a designed controller and a design method for the state feedback matrix were obtained．Based on this，a flowchart of the robust model predictive controller is given．Finally，a robust asymptotic stable theory of the closedloop system is given．Theoretical analysis and simulation demonstrate the feasibility of the controller and the robust asymptotic stability of the system．

nonlinear perturbation；multi-state time-delay；discrete nonlinear system；state feedback control；model predictive control；liner matrix inequalitie

10．11990／jheu．201510071

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．020．html

TP273

A

1006-7043（2016）12-1685-06

周衛東，鄭蘭，廖成毅，等．多重狀態時滯系統的min-max魯棒預測控制［J］．哈爾濱工程大學學報，2016，37（12）:1685-1690．

2015-10-28．

2016-09-28．

國家自然科學基金項目（61102107；61374208）．

周衛東（1966-），男，教授，博士生導師；

鄭蘭（1982-），女，博士研究生．

鄭蘭，E-mail:zhenglan000＠163．com．

ZHOU Weidong，ZHENG Lan，LIAO Chengyi，et al．Min-max robust predictive control for multi-state time-delay systems［J］．Journal of Harbin Engineering University，2016，37（12）:1685-1690．