非線性轉子-密封系統動力學行為演變機理研究

李忠剛，陳照波，陳予恕，朱偉東，3，馬文生

（1．哈爾濱工業大學機電學院，黑龍江哈爾濱150001；2．哈爾濱工業大學航天學院，黑龍江哈爾濱150001；3．美國馬里蘭大學機械工程，美國巴爾的摩縣21250；4．中航工業集團公司沈陽發動機設計研究所，遼寧沈陽110015）

非線性轉子-密封系統動力學行為演變機理研究

李忠剛1，2，陳照波1，陳予恕2，朱偉東2，3，馬文生4

（1．哈爾濱工業大學機電學院，黑龍江哈爾濱150001；2．哈爾濱工業大學航天學院，黑龍江哈爾濱150001；3．美國馬里蘭大學機械工程，美國巴爾的摩縣21250；4．中航工業集團公司沈陽發動機設計研究所，遼寧沈陽110015）

旋轉機械廣泛應用于民用、航空、航天和航海等各個領域，其穩定的動力學行為是保證工程機械安全運行的前提。本文主要針對轉子-密封系統豐富的非線性動力學行為，利用非線性動力學等理論分析了轉子-密封系統發生Hopf分岔和1∶2亞諧共振等動力學行為的產生條件和機理，進一步給出了非線性轉子-密封系統由自激振動引發亞諧共振的動力學行為演變機理，并通過理論分析，闡明了轉子-密封系統的氣流阻尼和剛度等動力學參數對系統動力學穩定性的影響規律，同時也利用數值計算驗證了分析結果。其理論分析結果對實際工程振動分析和結構設計具有一定的理論指導意義。

轉子-密封系統；Muszynska氣流模型；非線性轉子動力學；多尺度法；Hopf分岔；亞諧共振；自激振動；臨界轉速

轉子系統在非線性力作用下的動力學行為非常豐富，因此國內外學者針對非線性轉子系統動力學特性做出了大量杰出的工作［1］。在包含非接觸式密封的高參數旋轉機械系統中由于氣體壓力、流速和溫度等參數較高，端部密封的氣流激振力非常復雜，在實際工程中有時會嚴重影響機組的正常運行［2］。然而對轉子-密封系統中氣流激振力的實驗研究比較困難，目前國內外只有部分學者根據相似性等原理設計了轉子-密封系統實驗臺并進行了相關數據測試［3-5］。在氣流激振力模型研究方面，Alford［6］在1965年首先提出了氣流激振的力學模型——Alford模型，雖然能很好地解釋了氣流激振的基本現象，但Alford模型為線性模型。隨后，Rosenberg［7］提出了迷宮密封中流體的周向流動會激發出作用于轉軸上的擾動循環力。1986年，美國Bently公司的Muszynska［8］在大量轉子-密封系統流體實驗的基礎上，給出了流體激振力描述模型——Muszynska模型。此模型是一個非線性模型，雖然Muszynska模型很好的揭示密封中流體激振力的作用現象，但是其模型中含有多個需要通過實驗獲得的經驗參數，限制了此模型的廣泛適用性。在動力學分析方面，丁千等［9］應用Muszynska流體激振力模型建立的單盤轉子-密封系統，并利用中心流形定理和正規形理論研究了系統的Hopf分岔和自激振動等非線性動力學產生機理；馬輝等［10］應用數值計算的方法研究了轉子-軸承-密封系統在兩個不同載荷下存在多周期和分岔振動等豐富的動力學特性；何洪軍等［11］基于雙控體模型研究了轉子-密封系統動力學模型；王煒哲等［12］研究了實際工質氣體的密封力模型，并數值模擬了單盤轉子系統的動力學特性。Hopf分岔理論與多尺度法等動力學理論和方法研究非線性轉子-密封系統的周期解特性，并結合數值方法描述轉子-密封系統動力學特性，闡明數值計算中的非線性動力學特性的演變規律。

1 轉子-密封系統動力學模型及HOPF分岔分析

首先建立Jeffcott轉子-密封系統非線性動力學模型，如圖1所示，并考慮重力和不平衡質量對轉子的作用，系統動力學模型可表示為

式中:M為轉子質量，m為氣流慣性效應；Ke、De分別為轉軸的剛度和外阻尼；K、D為密封中氣流激振力的剛度和阻尼，K和D均為位移（x，y）的非線性函數為密封結構經驗系數；λ為密封中氣流的周向平均流速比，也為位移(x，y)的非線性函數，λ=λ0(1-e)b，b為密封結構經驗系數；mg為轉子自身重力；ρ為轉子平衡質量；r為不平衡質量半徑。可見系統（1）為非線性動力學系統，其動力學行為無法用傳統的八參數法完全描述。

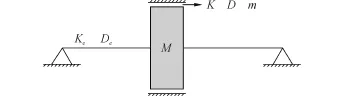
圖1 單盤轉子-密封結構模型Fig．1 Model of the rotor-seal system

首先將動力學系統（2）可表示成狀態方程形式為

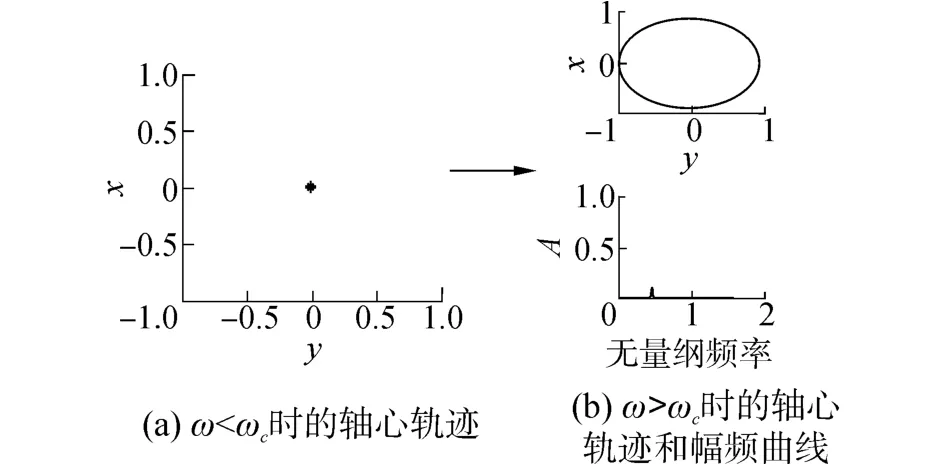
圖2 Hopf分岔前后系統狀態圖Fig．2 Analysis chart of system before and after Hopf bifurcation

2 轉子-密封系統1∶2亞諧共振理論分析

在實際工程中，不平衡轉子-密封系統會發生由氣流激振力誘發的低頻振動，導致系統出現1∶2亞諧共振。由于低頻振動的突發性和強烈振動（幅值較高），有時會嚴重影響機組的安全運行，因此對亞諧振動機理的產生研究是非常必要的。首先，將系統（2）在靜平衡點領域內進行冪級數展開，得到轉子-密封系統在平衡點領域內的冪級數表達形式，再考慮剔除影響較小的高階非線性項，則可得非自治的轉子-密封系統冪級數模型，可表示為

式中:ω1和ω2為系統固有頻率和為系統非線性力冪級數展開形式三次截斷表達式，Ω為系統外激勵頻率。

本文采用多尺度法來進一步研究系統（5）的周期解析解特性。設所求一次近似解形式為

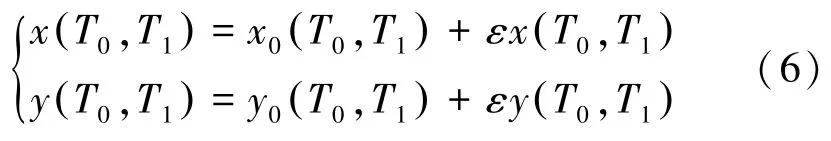
式中:Tn=εnt( n=0，1)為不同尺度的時間變量，T0為快時間變量，T1為慢時間變量。此時關于時間的導數為

將x、x′、x″和y、y′、y″代入動力學系統（5）中，由ε的同次冪系數可得:

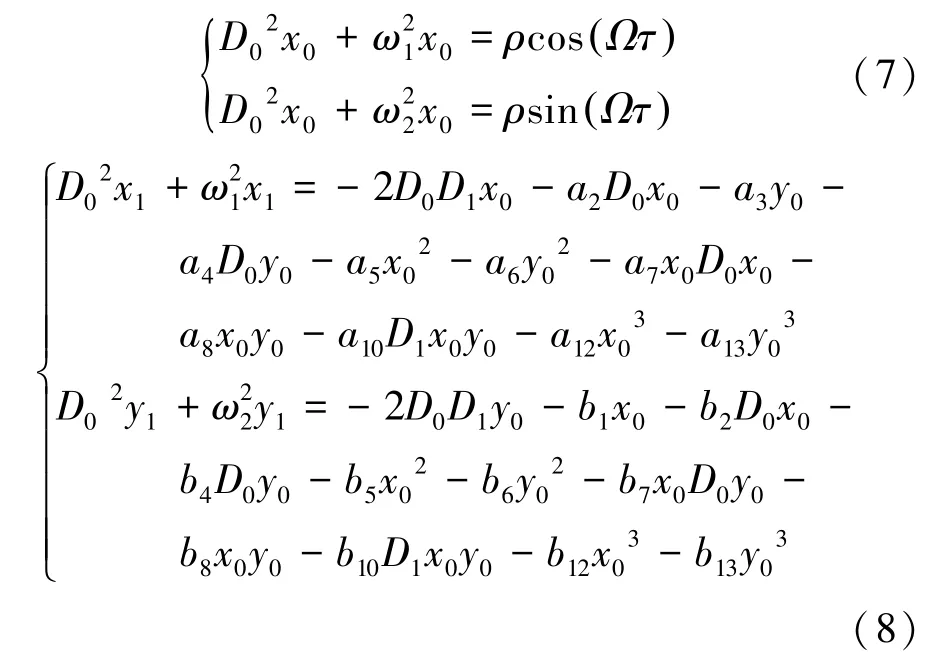
若系統存在1∶2亞諧共振，轉子的固有頻率ω為外激勵頻率的一半，即ω=1／2( Ω+σ)，σ為調諧參數。根據方程（7），解可設為

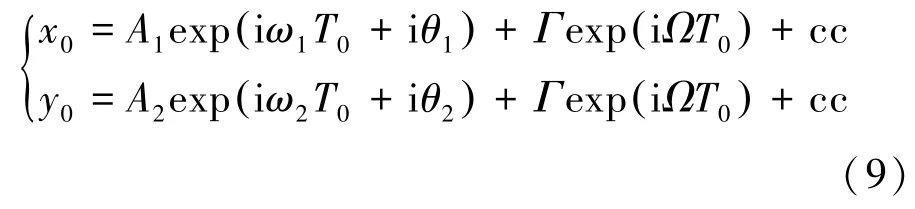
式中:A1、A2為時間變量Tn的函數，cc為前面部分的共軛表達式為激勵幅值項。為消除方程（8）中產生的長期項，必有:

可見式（10）中A1，A2的解相同，為分析方便可只分析第一個方程，將式（10）第一個方程的實部和虛部分離可得到:

其中φ=-2θ+2T0σ。由方程（9）消去相角項φ，系統（5）的分岔方程為

方程（12）非零解存在條件可以表示為

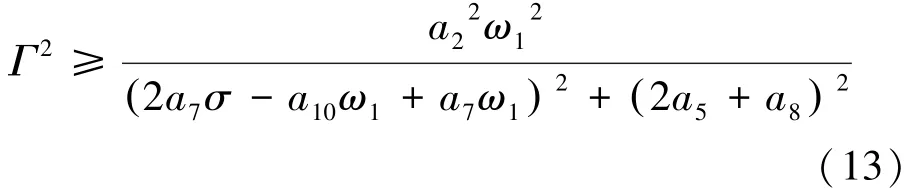
由此可知，由不平衡質量引起的同步周期振動會在非零解參數區域內被誘發出現1∶2亞諧共振。若轉子-密封系統不平衡質量很小，氣流激振力不會誘發系統出現亞諧共振現象或者可能發生亞諧共振的轉速較高；但當系統不平衡質量較大時，氣流激振力極易在轉子發生同步渦動時會誘發出亞諧振動成分。

3 轉子-密封系統非線性動力學演變機理及數值分析

當轉速較低時，轉子-密封系統在不平衡質量的作用下，只會發生同步運動，如圖3所示。且在一階固有頻率下，隨著轉速的提升振動幅值會明顯增加。隨著轉速升高，系統在臨界轉速ωc處會出現Hopf分岔，即此時會出現一個自激振動頻率成分，但由于自激振動頻率和轉速頻率可能不可約化導致系統出現擬周期運動，同時在Poincaré截面上出現閉合點集，在頻譜上能看到兩個不可約化頻率峰值，如圖4所示。隨著轉速持續增加，系統的自激振動頻率會接近系統固有頻率，此時兩個頻率可以約化，系統會出現倍周期運動，如圖5所示。此時頻譜圖上的兩個頻率成分比值為1∶2。當轉速繼續增加，系統出現由低頻振動產生的極限環，頻譜圖上低頻振動幅值較高，此時系統的振動主要由自激振動已發的系統共振導致，如圖6所示，同時可見振動幅值有所增加，有多個頻率成分，系統會變得更加不穩定。

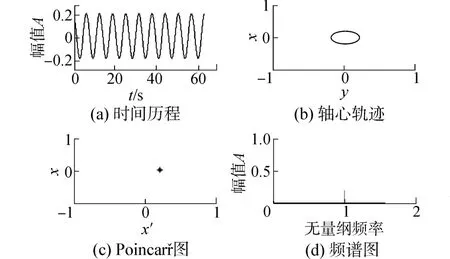
圖3 ω=120 rad／s系統分析圖Fig．3 Analysis charts of system with ω=120 rad／s

圖4 ω=295 rad／s系統分析圖Fig．4 Analysis charts of system with ω=295 rad／s

系統的不平衡質量是外激勵主要因素，其大小對系統的動力學影響如圖7所示。從圖中可以看出，當外激勵幅值較大時，如圖7中Γ=0．4時所示，系統會發生超臨界的Hopf分岔行為，即非零解與零解分別出現在Hopf分岔點的兩側；當外激勵幅值減小后，如圖7中Γ=0．18時所示，系統發生亞臨界Hopf分岔行為，即非零解與零解出現在Hopf分岔點附近的同一側；當外激勵幅值再進一步減小后，如圖7中Γ=0．1時所示，系統會在分岔點附近發生振動幅值跳躍的現象，且會存在兩個不同的振動幅值，此時系統會發生倍周期運動。外激勵幅值大小會改變系統發生亞諧振動的臨界轉速閾值，隨著外激勵幅值的減少，發生亞諧共振的轉速會隨之增加，由式（13）也可知系統亞諧振動非零解的起始點與外激勵幅值大小有關。綜上可知，轉子系統在進行了較好的動平衡后，在恒定工作轉速附近不易出現亞諧共振。但如果轉子-密封系統在運行過程中發生其他動力學參數改變可能會導致系統臨界轉速降低或系統轉速持續提高等，在動平衡較好的轉子-密封系統上一旦產生亞諧振動，其振動幅值將會增加較快，甚至會發生跳躍現象，導致系統不穩定。在工程實際中，汽輪機組曾經出現過:一旦機組發生由氣流激振引起的亞諧共振，系統振動幅值將會突然增大，短時間內就導致系統嚴重的失穩現象。

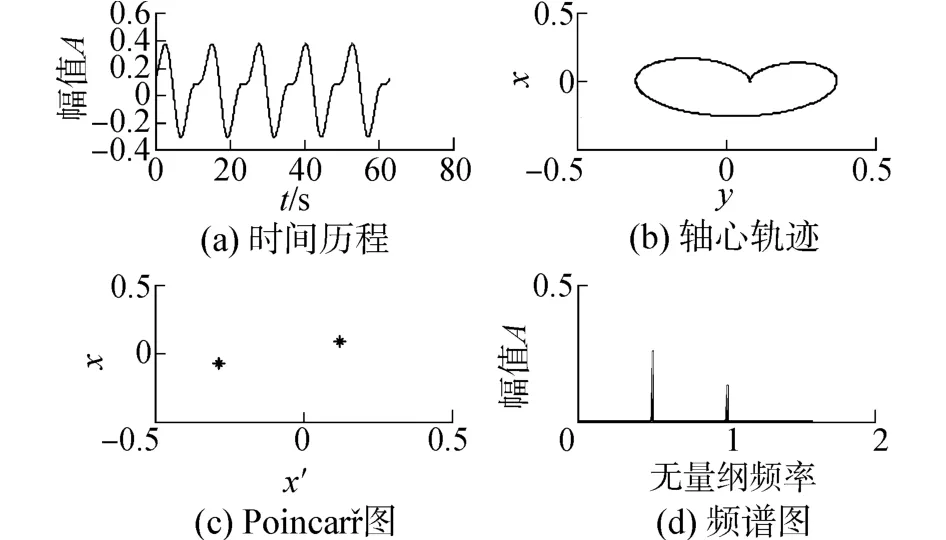
圖5 ω=310 rad／s系統分析圖Fig．5 Analysis charts of system with ω=310 rad／s

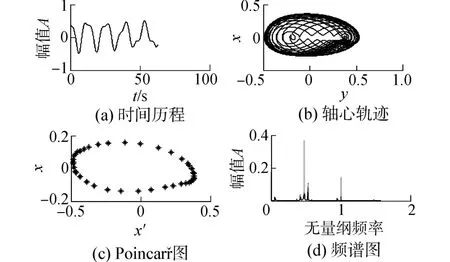
圖6 ω=470 rad／s系統分析圖Fig．6 Analysis charts of system with ω=470 rad／s

20世紀90年代，美國Texas大學Iwatsubo等［14］開展了大量實驗，通過改變密封結構增加氣流阻尼來抑制氣流激振，但實驗結果非常不理想。根據系統分岔方程（12），得到了系統在不同非線性剛度系數下，氣流阻尼對系統發生亞諧振動位置的影響，如圖8所示。不同的氣流激振力阻尼會導致系統發生亞諧振動的轉速不同；但是當非線性剛度發生變化后，氣流阻尼對動力學系統分岔點（臨界轉速）的影響也會不同，甚至可能會出現相反的作用效果。如圖8所示。因此可見轉子-密封系統中氣流阻尼對系統分岔點的影響，需要根據系統其他動力學參數而確定。

圖7 外激勵幅值對系統的影響Fig．7 Effect of the exitation amplitude on the system

圖8 氣流阻尼對系統的影響Fig．8 Effect of the gas damping on the system

4 結論

1）本文建立了轉子-密封系統非線性動力學模型，根據Hopf分岔條件，給出轉子-密封系統發生周期解失穩的臨界轉速計算公式，通過計算公式可知密封激振力對系統動力學顯著；

2）進一步應用非線性振動中的多尺度方法研究轉子-密封系統動力學解析解表達式，由平均方程獲得了轉子-密封系統分岔方程；

3）由分岔方程獲得了系統非零解的判斷條件，即發生Hopf分岔和1∶2亞諧共振產生條件，闡明了轉子-密封系統非線性動力學產生機理；

4）利用數值計算方法詳細闡明了轉子-密封系統的自激振動與亞諧共振動力學行為演變規律；

5）根據轉子-密封系統分岔方程理論分析了氣體阻尼增加未必會增加系統穩定性的原因，此理論分析結果與美國Texas大學實驗結論一致。

本文的分析結果對實際工程振動分析和設計具有一定的理論指導意義。

［1］黃文虎，武新華，焦映厚，等．非線性轉子動力學研究綜述［J］．振動工程學報，2000，13（4）:497-509．HUANG Wenhu，WU Xinhua，JIAO Yinghou，et al．Review of nonlinear rotor dynamics［J］．Journal of vibration engineering，2000，13（4）:497-509．

［2］DIMAROGONAS A D，GOMEZ-MANCILIA J C．Flow-excited turbine rotor instability［J］．International journal of rotating machinery，1994，1（1）:37-51．

［3］MARQUETTE O R，CHILDS D W，SAN ANDRES L．Eccentricity effects on the rotordynamic coefficients of plain annular seals:theory versus experiment［J］．Journal of tribology，1997，119（3）:443-447．

［4］曹浩，楊建剛，郭瑞，等．密封動力特性系數試驗識別方法及影響因素分析［J］．機械工程學報，2011，47（9）:85-89．CAO Hao，YANG Jiangang，GUO Rui，et al．Experimental identification method and influence factor analysis of seal dynamic characteristic［J］．Journal of mechanical engineering，2011，47（9）:85-89．

［5］KWANKA K．Dynamic coefficients of stepped labyrinth gas seals［J］．Journal of engineering for gas turbines and power，2000，122（3）:473-477．

［6］ALFORD J S．Protecting turbomachinery from self-excited rotor whirl［J］．Journal of engineering for power，1965，87（4）:333-343．

［7］ROSENBERG C．Investigating aerodynamics transverse force in labyrinth seals in case involving rotor eccentricity．C．E．Tran．083［J］．Translated from Energnmashinostrojohic，l974，8:15-17．

［8］MUSZYNSKA A．Whirl and whip—rotor／bearing stability problems［J］．Journal of sound and vibration，1986，110（3）:443-462．

［9］DING Q，COOPER J E，LEUNG A Y T．Hopf bifurcation analysis of a rotor／seal system［J］．Journal of sound and vibration，2002，252（5）:817-833．

［10］MA Hui，LI Hui，NIU Heqiang，et al．Nonlinear dynamic analysis of a rotor-bearing-seal system under two loading conditions［J］．Journal of sound and vibration，2013，332（23）:6128-6154．

［11］何洪軍，荊建平．非線性轉子-密封系統動力學模型研究［J］．振動與沖擊，2014，33（10）:73-76．HE Hongjun，JING Jianping．Dynamic model of a nonlinear rotor-seal system［J］．Journal of vibration and shock，2014，33（10）:73-76．

［12］WANG Weizhe，LIU Yingzheng，JIANG Puning．Numerical investigation on influence of real gas properties on nonlinear behavior of labyrinth seal-rotor system［J］．Applied mathematics and computation，2015，263:12-24．

［13］李忠剛，孔達，焦映厚，等．轉子-密封系統非線性動力學特性分析［J］．振動與沖擊，2009，28（6）:159-163．LI Zhonggang，KONG Da，JIAO Yinghou，et al．Research on nonlinear dynamic characteristics of a rotor-seal system［J］．Journal of vibration and shock，2009，28（6）:159-163．

［14］IWATSUBO T，FUKUMOTO K，MOCHIDA H．An experimental study of dynamic characteristics of labyrinth seal，NASA CP-3239［R］．NASA，1993:219-238．

Study on the mechanism and transformation of the dynamic behavior in a nonlinear rotor-seal system

LI Zhonggang1，2，CHEN Zhaobo1，CHEN Yushu2，ZHU Weidong2，3
（1．School of Mechatronics Engineering，Harbin Institute of Technology，Harbin 150001，China；2．School of Astronautics，Harbin Institute Technology，Harbin 150001，China；3．University of Maryland，Mechanical Engineering，Baltimore County 21250，USA；4．AVIC Shenyang Aeroengine Research Institute，Shenyang 110015，China）

Rotating machinery is widely used in civilian，aviation，aerospace，navigation，and other fields，and the stability behavior of the system dynamics is a prerequisite guaranteeing safe operation．In this paper，by using nonlinear dynamics theories，complicated transformation of the dynamic behaviors，Hopf bifurcation and 1∶2 sub-harmonic resonance，was investigated on a rotor-seal system，and the conditions and mechanism of the dynamic behavior were obtained．Furthermore，the evolution of subharmonic resonance dynamics in the nonlinear rotor-seal system caused by self-excited vibration was analyzed．Based on the theoretical analysis，it is observed that the damping and stiffness parameters of the nonlinear rotor-seal system affect its system stability dynamics．Finally，numerical calculation verifies the results from the theoretical analysis．It is significant that the results of the theoretical analysis can explain the vibration behavior of the system and guide the structural design of the system in practical engineering．

rotor-seal system；Muszynska′s gas model；nonlinear rotor dynamics；multiscale method；Hopf bifurcation；sub-harmonic resonance；self-excited vibration；critical speed

10．11990／jheu．201510041

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．006．html

O347．6

A

1006-7043（2016）12-1704-05

李忠剛，陳照波，陳予恕，等．非線性轉子-密封系統動力學行為演變機理研究［J］．哈爾濱工程大學學報，2016，37（12）:1704-1708．

2015-10-19．

2016-09-28．

國家自然科學基金項目（11302058；11272100）；中國博士后面上基金項目（2013M541360）．

李忠剛（1982-），男，助理研究員，博士．

李忠剛，E-mail:lizhonggang＠hit．edu．cn．

LI Zhonggang，CHEN Zhaobo，CHEN Yushu，et al．Study on the mechanism and transformation of the dynamic behavior in a nonlinear rotor-seal system［J］．Journal of Harbin Engineering University，2016，37（12）:1704-1708．