空氣聲源激發的淺海聲場的理論研究
周 偉
(中國艦船研究設計中心,湖北武漢 430064)
0 引 言
水聲探測反潛直升機是國內外水聲工作者研究的熱點之一。直升機輻射噪聲的頻譜是連續譜與強線譜[1-2]的疊加,尤其是在低頻段強線譜豐富。
目前公開發表的文獻中,水聽器探測直升機作用距離約為300 m[3-5],關于該結果一般采用射線理論解釋,認為由于空氣水界面處存在約為13° 的透射臨界角,水聽器僅能接收在此臨界角范圍內的飛機輻射噪聲。
對空氣、水和海底進行三層介質空間建模,利用波動理論求解直升機激發水下聲場的報道并不多見,Michael J. Buckingham曾在美國聲學雜志J.A.S.A上發表過相關內容的研究[6],他將空氣、水和海底建模為三層均勻介質空間,利用波動理論推導了聲場的形式解,并在此基礎上做了相關的研究,包括等效深度、以及聲源運動對水下聲場的各種影響等內容。作者在典型淺海及飛機輻射強線譜條件下,利用“有效深度”的概念得出水中有三階波導簡正波。若有波導簡正波存在,必能以較小傳播損失遠程傳播。這與作者先前發表的文獻[4-5]中利用射線理論解釋實驗結果有重大差別。作者沒有仔細甄別這兩種差別。
實際情況下,海面上空氣由于溫度、風等因素的影響,其聲速分布并非均勻的。為進一步分析空氣中聲速分布對直升機激發的水下聲場的影響,本文將空氣中聲速分布假設為 Epstein分布[7-9],海水和海底聲速分布假設為均勻分布,并利用波動方程求解聲場形式解,分析了聲壓場及振速場的特性。
1 三層Pekeris介質模型
三層介質Pekeris介質模型如圖1所示[6],z軸向下為正,海面為平面,聲源S坐標為其中,海深為H,如無特殊說明本文中指淺海,接收點R坐標為(r,z)。空氣、海水和海底為均勻介質,聲速和密度均為常量,分別為
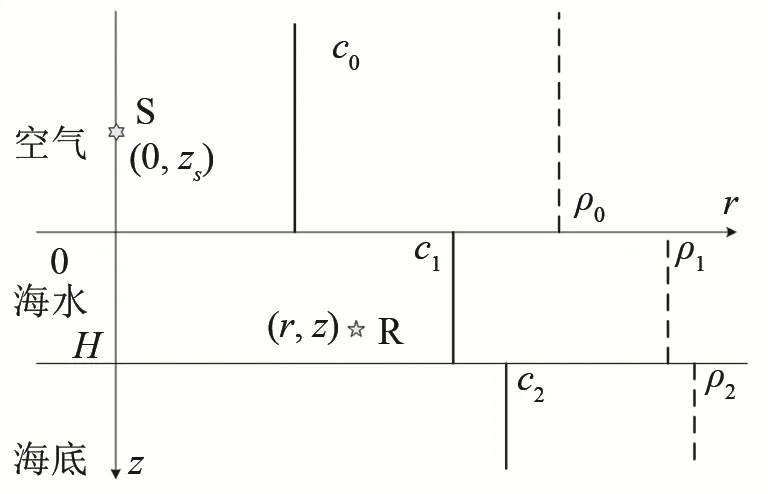
圖1 三層pekeris模型Fig.1 Three-layers Pekeris model
2 Epstein介質模型
空氣中聲速為 Epstein分布的三層介質模型如圖2所示,水層和海底的建模與三層Pekeris介質模型相同。空氣的密度這里同樣認為是常量ρ0,下文將該模型簡稱為“Epstein模型”,空氣中的聲速建模為Epstein分布。
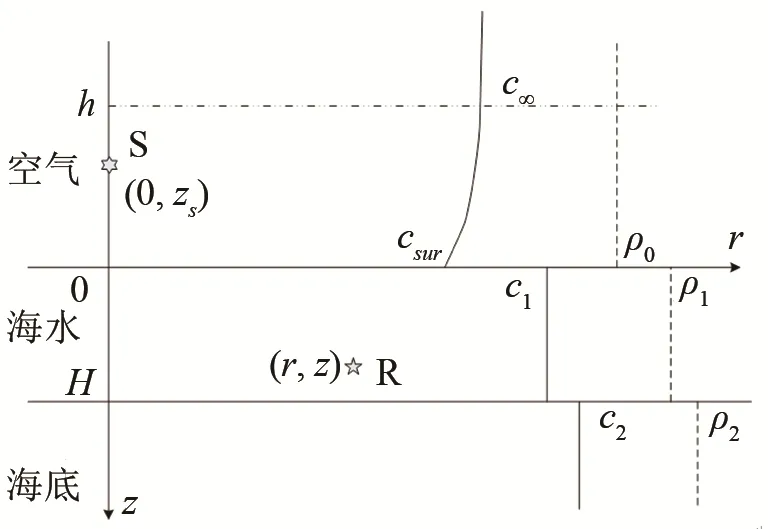
圖2 空氣中聲速為Epstein分布的三層介質模型Fig.2 Three-layer medium model with Epstein sound speed distribution in air
Epstein聲速分布表示式如式(1)所示。
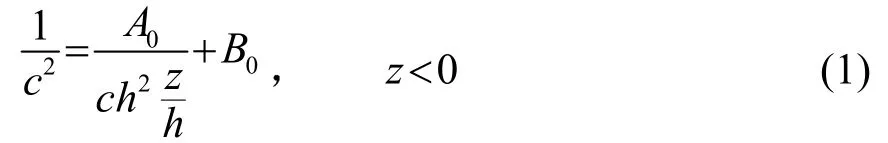
設空氣中各點密度相同,并假定聲速僅與直角坐標系(x,y,z)的 坐標有關。式(1)中是描述介質的參數,其中表示海面處空氣的聲速,c∞表示高空空氣聲速,h表征空氣中波導層的厚度。一般將的情況稱為Epstein波導,將的情況稱為Epstein反波導,而當時,空氣層為均勻聲速分布,此時Epstein模型與三層Pekeris介質模型相同。
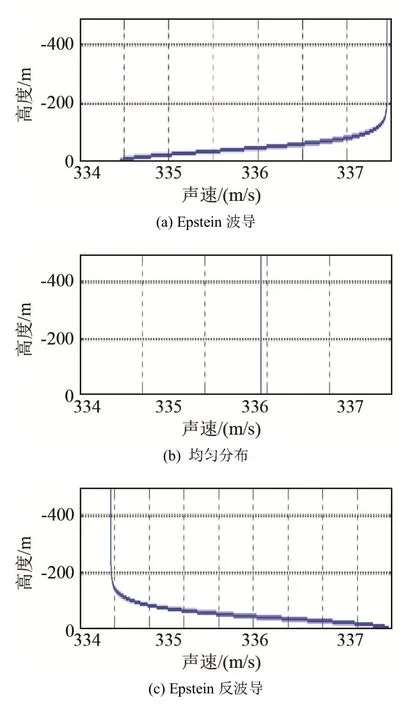
圖3 不同條件下的Epstein聲速分布Fig.3 Epstein sound speed distributions under different conditions
所以三層Pekeris介質模型可以看做是Epstein模型的一種特例。
3 聲場形式解的推導與分析
下面分析在上述兩種不同模型下,空氣中點源激發的聲場的形式解,取時間因子為e?jωt, 表示速度勢函數,在柱坐標系中頻域波動方程為:
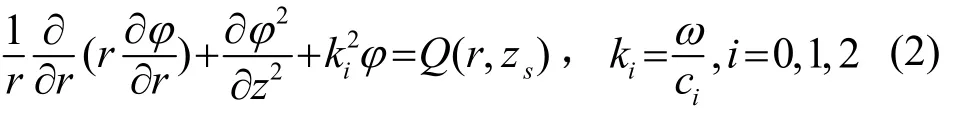
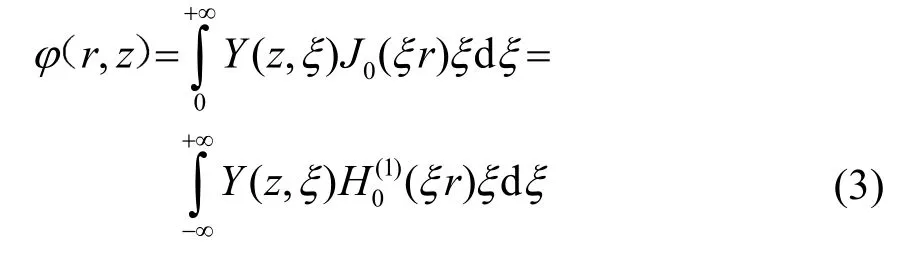
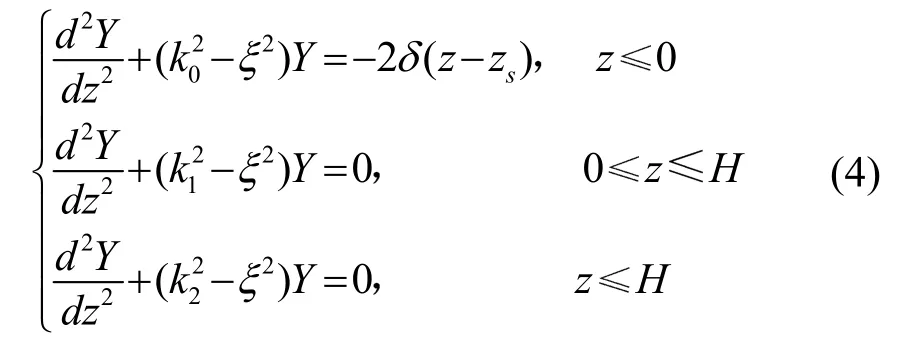
其中:ξ表示水平波數。記:為第i層介質中垂直方向波數。或稱ξ為波數水平分量,βi為波數的垂直分量。
3.1 三層Pekeris介質模型下的聲場解
在三層 Pekeris介質模型下,將Y(z,ξ)的通解表示為:
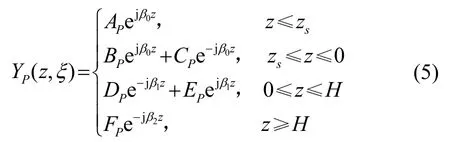
下腳標“P”表示三層Pekeris模型下的結果。利用邊界條件如式(6)所示和點源條件如式(7)所示(邊界條件與所建模型無關,故未加腳標):
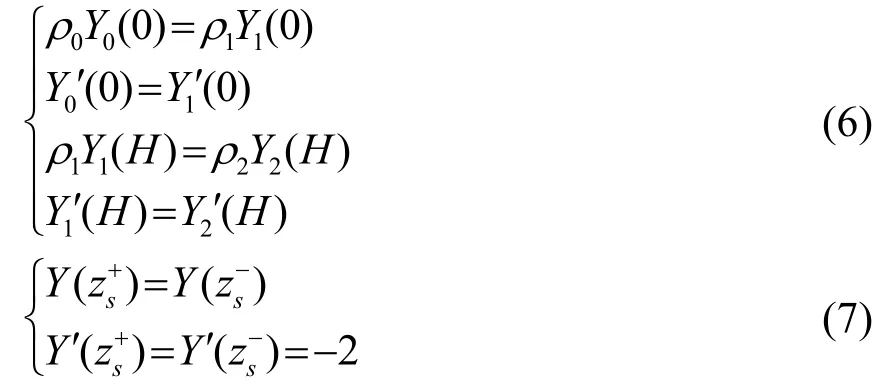
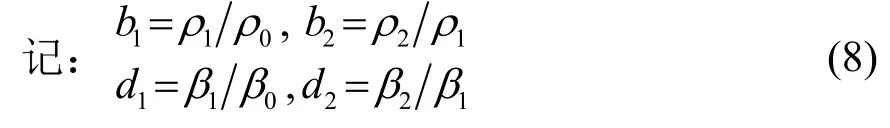
則水層和海底的速度勢函數為:

其中
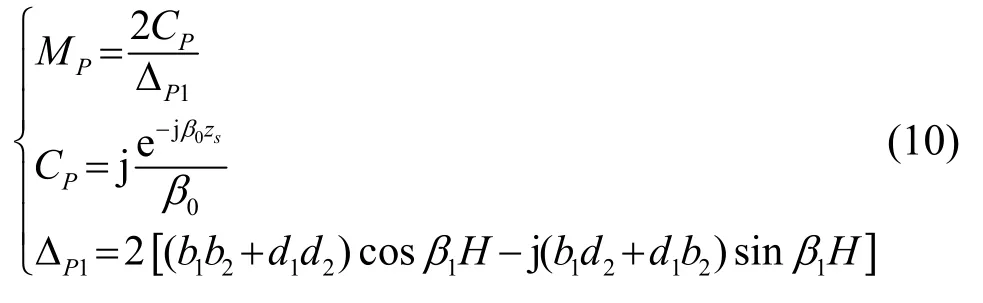
式中:?P1的下腳標“1”表示與水層波導相關的結果,若令即為水層波導簡正波的頻散方程,下文稱此類本征值對應的簡正波為水波。
3.2 Epstein模型下的聲場解推導
因空氣中聲速服從Epstein分布,如式(1)所示,聲場可以表示為[7]:
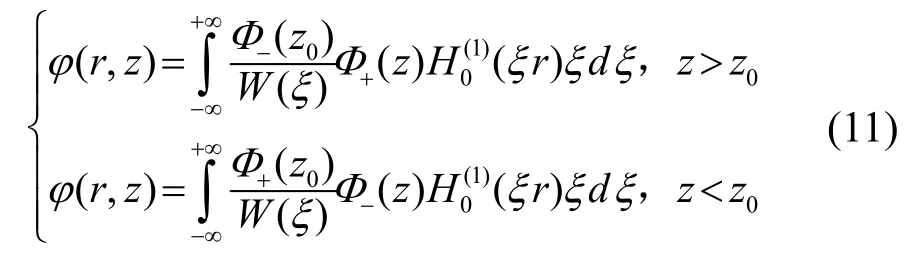
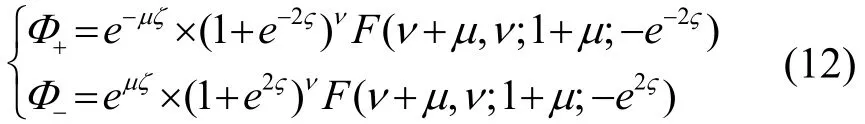
其中:“F(.)”表示超幾何方程,約定當ξ為實數時取Re(μ)≥0及Im(μ)≤0。當A→0時,ν=1代表均勻空間,此時有

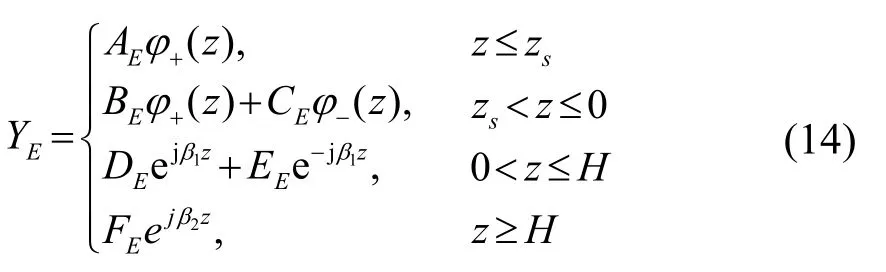
其中:下腳標“E”表示Epstein模型下得到的結果,的定義與式(8)相同,與式(12)中的表示形式相同。
利用式(6)、(7)所示的邊界條件和點源條件可得水層和海底的速度勢函數為:
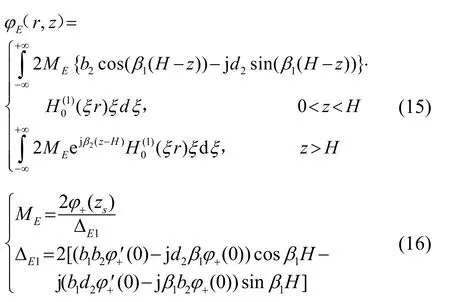
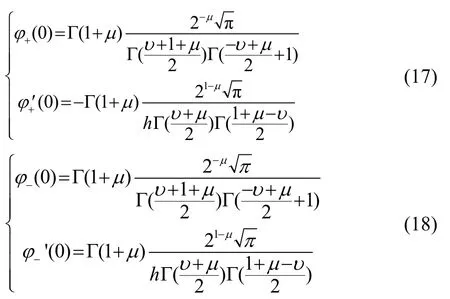
而對于空氣中的 Epstein波導層中存在的簡正波,其本征方程由朗斯基行列式為零得到[7],即:
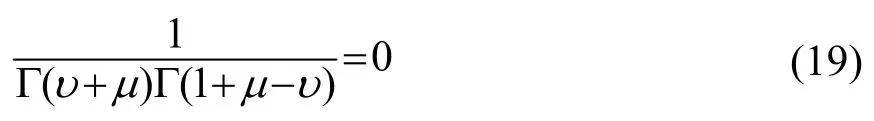

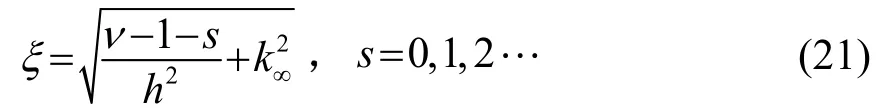
文中將此類本征值對應的在水中傳播的波稱為“水面波”,在水層中為非均勻波,在空氣中為Epstein波導簡正波。該類波在水層中近水面處強度大,隨著深度的增加,其強度激劇減小,所以稱之為“表面波”。
4 水層中兩種波的分析與數值計算
對比兩種不同模型下的結果,可以發現將空氣中聲速分布建模為 Epstein分布時,空氣中點源所激發的水下聲場存在水波和水面波,而三層Pekeris介質模型的結果,空氣中點源所激發的遠程水下聲場僅含有水波,近程有側面波。下面具體分析這兩類波的特點。
4.1 水 波
由式(10)和(16)可得兩種模型下水波的頻散方程為
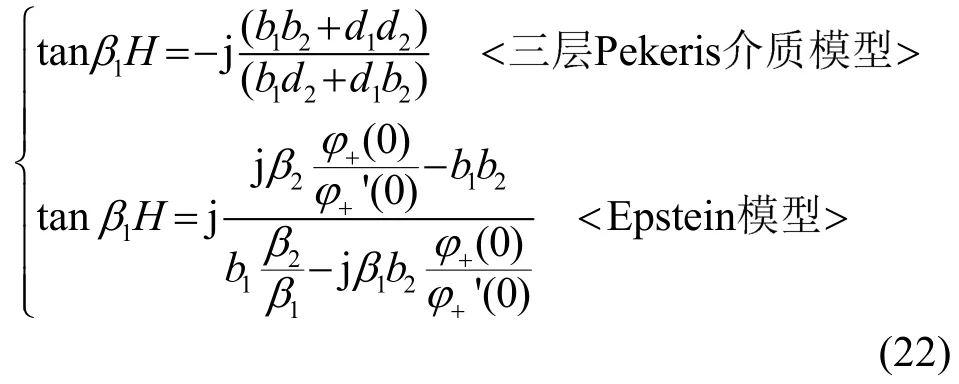

從式(23)可以看出空氣中的聲速分布對水波的影響不大。下面給一個具體算例。
算例1條件:海深H= 50m;影響空氣中Epstein波導厚度參數h=? 50m;海水中聲速為c1=1 500 m/s;密度ρ1= 1 000kg/m3;海底聲速為c2= 1600m/s;密度ρ2= 1800kg/m3;空氣密度ρ0= 1.25kg/m3。空氣中聲速與溫度關系:c= 331.45+ 0.6t,t單位為℃,假設海面處空氣溫度為 5℃,高空中空氣溫度為10℃,所以有c0=334.450 0 m/s,c∞=337.450 0 m/s。聲源參數zs=?8 0m,點源頻率為 100 Hz,由此可得水層中存在的兩階波導簡正波的本征值為:0.417 940、0.415 069。
圖4為兩種不同模型下,水波的前兩階波導簡正波的聲壓歸一化幅度沿垂直方向的分布對比。
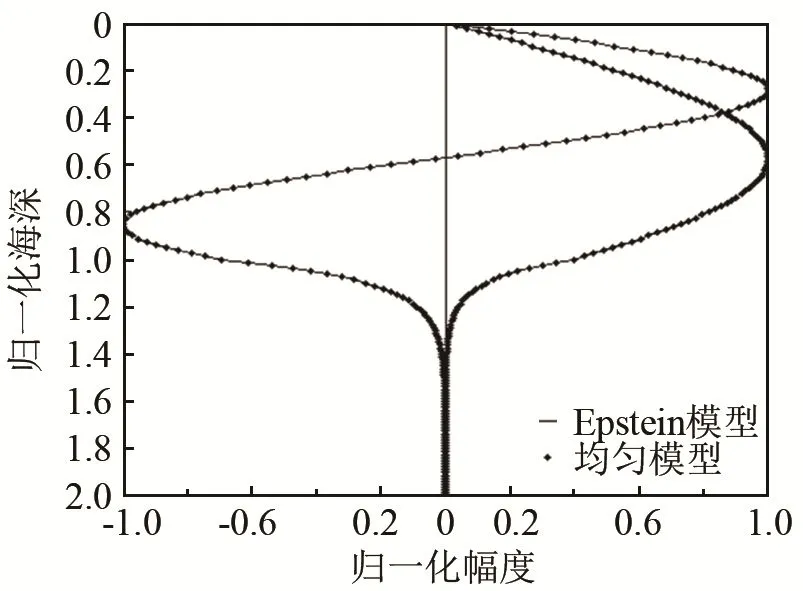
圖4 兩種模型下水波前兩階簡正波的歸一化幅度在垂直方向的分布Fig.4 Normalized amplitude distributions of the first two order modes of water wave in the vertical direction under two models
從圖4中可以發現,在兩種不同模型下,水波的簡正波振幅在深度方向分布的歸一化幅度分布關系相同。
圖5為當c∞=c0,其他條件與算例1相同時,水波的前兩階簡正波的聲壓的垂直分量沿垂直方向的歸一化幅度對比。
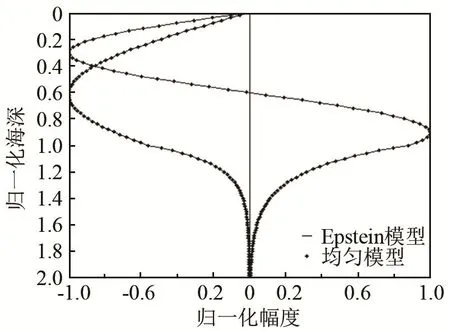
圖5 兩種模型下水波歸一化幅度對比Fig.5 Comparison between the normalized amplitude distributions of water wave under two models
從圖中可以看出兩種不同模型得到的結果完全一致,說明三層 Pekeris介質模型是本文所建的Epstein模型的一種特例。
4.2 水面波
式(21)給出了水面波本征值的計算方法,下面給出一個具體的算例結果。數值計算條件與算例 1相同。當頻率為20 Hz時,在空氣層中共有5階Epstein波導簡正波,本征值依次為:0.374 640、0.372 983、0.372 877、0.372 393、0.374 431,故在水層中存在5階相應的水面波。圖6為前兩階水面波的聲壓,在水層中的歸一化幅度與深度的關系圖,這里以第一階水面波在水中幅度最大值為參考。

圖6 前兩階水面波的歸一化幅度在垂直方向的分布Fig.6 Normalized amplitude distributions of the first two orders of surface water wave
從圖6中可以看出空氣中點源激發的水面波是一種非均勻波,隨著深度的增加強度逐漸減小,而且隨著頻率的升高衰減速度將加快。
4.3 傳播損失數值計算
下面給出的數值計算結果的條件與算例1中相同,圖7(a)、7(b)為三層Pekeris介質模型和Epstein模型下聲壓傳播損失的計算結果,接收深度分別為1 m、15 m和25 m,以聲源正下方1 m處的聲強為參考。
由圖7可以看出,當接收深度較深時,兩種模型下的傳播損失基本相同,而在近海面處兩種不同模型下的傳播損失差別較大,這說明了此時水面波起到了主要作用。
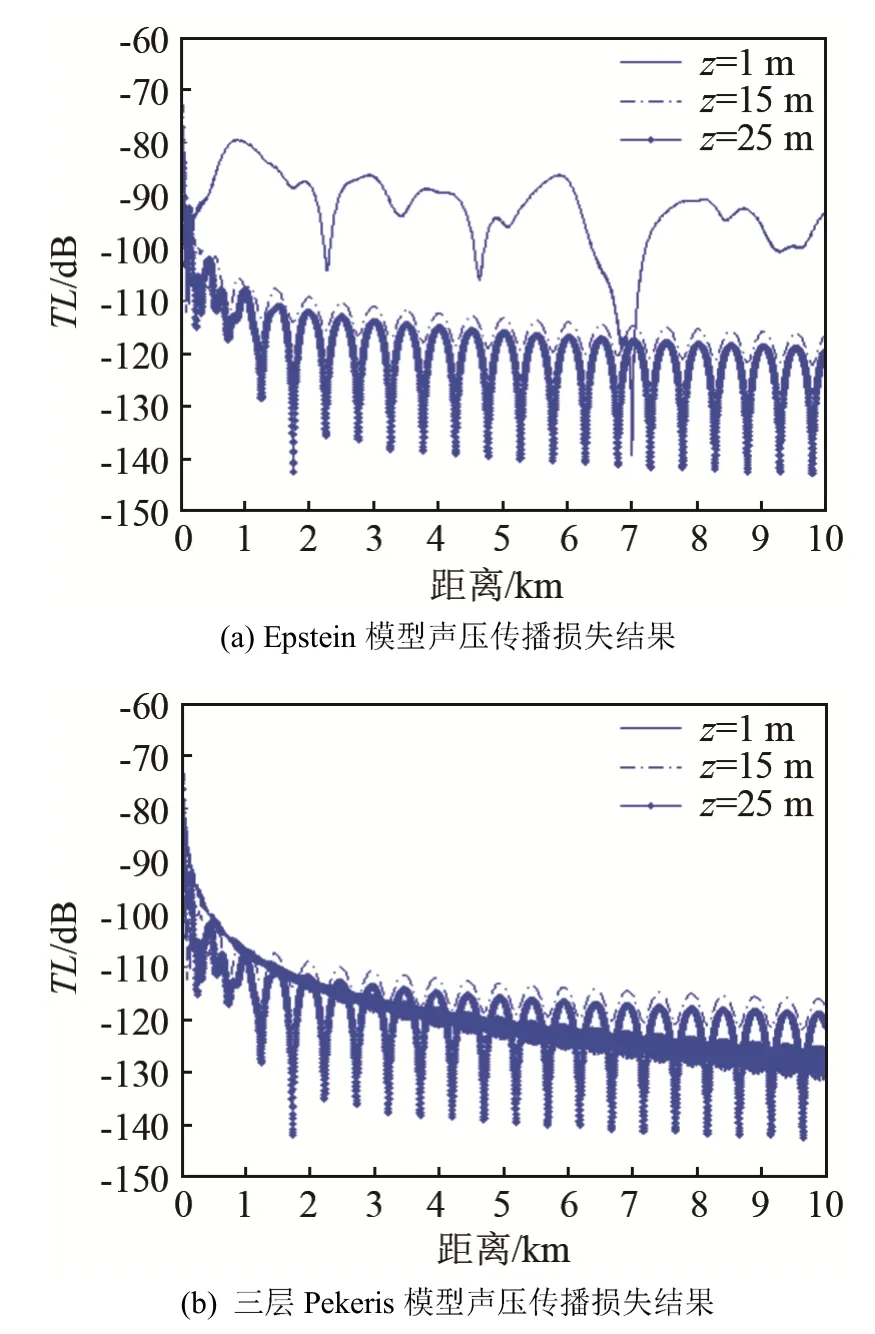
圖7 兩種不同模型下不同接收深度聲壓傳播損失對比Fig.7 Comparison of transmission loss at different depths undertwo models
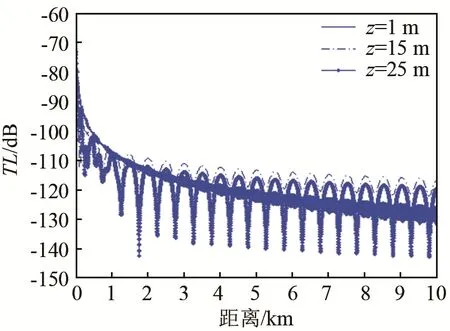
圖8 Epstein模型下,假定空氣中聲速為均勻分布時不同接收深度傳播損失對比Fig.8 Comparison of transmission loss at different depths under the Epstein model with a uniform sound velocity distribution in air
圖8為Epstein模型下,假設空氣中聲速分布為均勻分布時,聲壓在不同接收深度的傳播損失,以聲源正下方1 m處聲強為參考。
將圖8的結果與圖7(b)對比可以發現,兩者的傳播損失相同,進一步證明了,三層Pekeris介質模型是Epstein模型的一種特例。
5 結 論
本文對空氣、水和海底三層介質進行了建模,將空氣中聲速分布假定為 Epstein分布,水層和海底假定為均勻分布,并經推導得出了聲場的聲壓形式解。與文獻中的三層Pekeris介質模型結果相比,本文所得結果分析了空氣中聲速分布對空氣中聲源激發水下聲場的影響,即存在水面波。而三層Pekeris介質模型的結果是本文所得結果的一種特例,用數值計算的方法對其進行了驗證。
[1]R. J. Urick. Noie signature of an aircraft in level flight over a hydrophone in the sea[J]. J. Acoust. Soc. Am., 1972, 52(3): 993- 999.
[2]王華明, 張強, 胡章偉, 等. 直升機飛行噪聲的試驗研究[J]. 聲學學報, 2003, 28(3): 177-181.
WANG Huaming ZHANG Qiang, HU Zhangwei, et al. An experiment study of AS350B2 helicopter noise[J]. ACTA, 2003,28(3): 177-181.
[3]Buckingham M J. Acoustical remote sensing of the sea bed using propeller noise from a light aircraft[M]// H. Medwin. Sounds in the Sea: From Ocean Acoustics to Acoustical Oceanography. Cambridge Cambridge University Press, 2005: 581-597.
[4]Buckingham M J, Giddens E M, Simonet F, et al. Propeller noise from a light aircraft for low-frequency measurements of the speed of sound in a marine sediment[J]. J. Comput. Acoust., 2002, 10(1):445-464.
[5]Buckingham M J, Giddens E M, Pompa J B, et al. Sound from a light aircraft for underwater acoustics experiments[J]. Acta. Acust.Acust., 2002, 88(4): 752-755.
[6]Michael J. Buckinghamam, Eric M. Giddens. Theory of sound propagation from a moving source in a three-layer Pekeris waveguide[J]. J. Acoust. Soc. Am., 2006, 120(4): 1201825-1841.
[7]布列霍夫斯基赫著, 楊訓仁譯. 分層介質中的波[M]. 2版. 北京:科學出版社, 1985.
BREKHOVSKIKH L M. Waves in layered media[M]. 2ndEdition.Beijing: Science Press, 1985.
[8]周偉. 直升機激發水下聲場的理論及實驗研究[D]. 哈爾濱: 哈爾濱工程大學, 2010.
ZHOU wei. Study of theory and experiment of underwater acoustic field excited by a helicopter[D]. Harbin: Harbin Engineering University, 2010.
[9]周偉. 空氣中聲速為Epstein分布的空氣中聲源激發的水下聲場分析[C]//中國聲學學會水聲分會2013年全國水聲學術會議論文集.
ZHOU wei. The study of underwater acoustic field excited by a source in the air with Epstein distribution[C]//The 2013 national conference on underwater acoustics proceedings, 2013.

