基于粒子群優化算法的旋轉導彈姿態修正策略

張 泓，郭正玉

(1.空軍駐黑龍江地區軍事代表室，哈爾濱 150000； 2.中國空空導彈研究院，河南 洛陽 471000)

【裝備理論與裝備技術】

基于粒子群優化算法的旋轉導彈姿態修正策略

張 泓1，郭正玉2

(1.空軍駐黑龍江地區軍事代表室，哈爾濱 150000； 2.中國空空導彈研究院，河南 洛陽 471000)

針對某型無控火箭彈，對其進行制導化改造并設計了基于粒子群優化算法的直接力裝置工作策略，建立彈體六自由度模型，并進行仿真分析，研究結果表明所設計的直接力點火策略能夠保證彈體穩定的前提下，有效減小落點散布，為無控火箭彈制導化改造的控制策略設計及其工程化應用提供了參考。

旋轉導彈；直接力；粒子群優化；仿真分析

現代戰爭中，來自空中的威脅多種多樣，除了傳統的飛機和武裝直升機等大型目標外，巡航導彈、無人機等也在戰爭中起著重要的作用。除此之外，飛艇、浮空器等新型目標也都是戰爭中應該防范的低小慢目標種類。空空導彈有著極高的命中率，能夠在戰爭中有效地打擊空中目標。然而，其價格十分昂貴，如果大量使用空空導彈打擊低小慢目標，將會給作戰帶來巨大的經濟負擔。

目前，我國現存大量的火箭彈、炮彈等無控彈藥。這類彈藥，其特點是彈體自身在飛行過程中，通常采用斜置尾翼、弧形尾翼或者發動機噴管傾斜等方式使彈體以一定的旋轉角速度繞縱軸旋轉，由于飛行過程中始終處于無控狀態，彈藥的落點散布相對大。但是，彈體旋轉能夠降低發動機推力偏心和質量偏心等干擾因素造成的影響，提高動穩定性。針對無控彈藥，加入小型化的制導部件，利用旋轉特性，提高其打擊精度是一種可行的新型武器發展方向。這種帶有制導化部件的低成本導彈，不但能夠有效地打擊防區內的多種低小慢空中目標，而且能夠兼顧打擊幾十公里內的近距地面目標，此外火箭彈等無控彈藥與空空導彈等精確制導武器相比成本低，因此，采用制導化方法提高旋轉導彈的打擊精度，使其具備打擊高價值軍事目標的精確打擊能力，具有顯著的軍事意義和經濟價值。

目前，世界各國針對這一研究領域開展了大量的研究工作。針對不同的需求，國內外已經出現了多種艦載、便攜式和反坦克導彈型號產品。在20世紀80年代，美國裝備了“銅斑蛇”末制導炮彈?！般~斑蛇”末制導炮彈由155 mm榴彈炮發射，采用激光半主動尋的制導方式，是世界上較早的末制導炮彈之一，主要用于攻擊集群坦克或裝甲車等地面目標。1991年海灣戰爭中，美國發射了約90枚“銅斑蛇“制導炮彈，彈無虛發摧毀敵對目標，為奪取戰爭優勢起到積極作用。此后，美國不斷開展對低成本導彈技術的研究，主要代表型號有“神劍”制導彈藥，“XM395精確制導武器(PGMM)”。有報道稱，美國陸軍計劃與2015—2017年采購數萬枚該型精確制導彈藥，并將其部署在伊朗、阿富汗和以色列等中東國家，增強其對ISIS等恐怖組織目標的打擊能力。

蘇聯于20世紀80年代中期生產并裝備了“紅土地”制導彈藥。與美國“銅斑蛇”相比，其射程遠，質量輕。在1993年和1995年進行的發射試驗中，發射20發炮彈擊毀19輛坦克目標，命中率高達95%。近20年來，“紅土地”制導彈藥已成系列化產品，其威力、射程、精度等性能指標都有了大幅度提高。

在國內，從20世紀90年代開始，多家科研單位和高等院校都陸續開展了針對低成本制導武器的研究工作，進行了彈道解算與優化、修正機構設計、制導控制系統算法設計與仿真等關鍵技術的研究，取得了大量的研究成果[1-3]。

1 旋轉導彈制導化改造方案

1.1 控制方法和控制機構

通常，導彈采用三通道自動駕駛儀使其在飛行過程中彈體保持穩定姿態。基于火箭彈、炮彈等在飛行過程中彈體旋轉這一運動學特點，在彈體內部加入制導部件，使其具備能夠類似于導彈的精確打擊能力。

旋轉導彈在發動機點火后立即起旋，轉速大約為5～20 rad/s，彈體速度在很短時間(幾秒內)達到最大值。旋轉導彈提高打擊精確度是采用彈道修正技術。彈道修正技術是在飛行過程中實時測量彈體的位置信息，并將其與發射前彈體內部裝訂的預置彈道信息比對，得到彈道偏差信息，再將偏差量作為控制系統的反饋值，產生控制指令，控制執行機構動作，對實際彈道進行一次或多次修正，實現減小落點散布，提高打擊精度的功能。彈道修正力一般為附加空氣動力或脈沖推力，通常采用脈沖推力控制器、阻力環和舵面等機構實現修正功能。

目前，針對直接力裝置修正，已經在采用數值仿真計算脈沖發動機的修正閾值、脈沖工作個數、單個沖量大小、相鄰兩個脈沖之間的工作時間間隔等對彈道參數的影響等方面進行了分析研究。本文所研究的對于旋轉彈體的姿態修正，采用直接力裝置，在旋轉彈體頭部沿徑向布置多個脈沖推力器，作用時間為毫秒級，通過噴流反作用力為彈體提供直接力，其作用時間短、噴流速度大，設計與其適配的控制算法，能夠在短時間內達到調整彈體姿態，減小彈落點誤差目的。

1.2 坐標系和控制力方程

旋轉彈體工作時序與控制策略如圖1所示，執行機構由20個脈沖機構組成，動作的起始時刻由彈道偏差值決定，當偏差值大于系統所設定的允許值時，偏差信號將被控制系統轉化為發動機觸發信號，位于偏差方位上的脈沖機構工作，提供修正力調整彈體姿態，控制彈體在空間的運動，減小彈道偏差[4-6]。

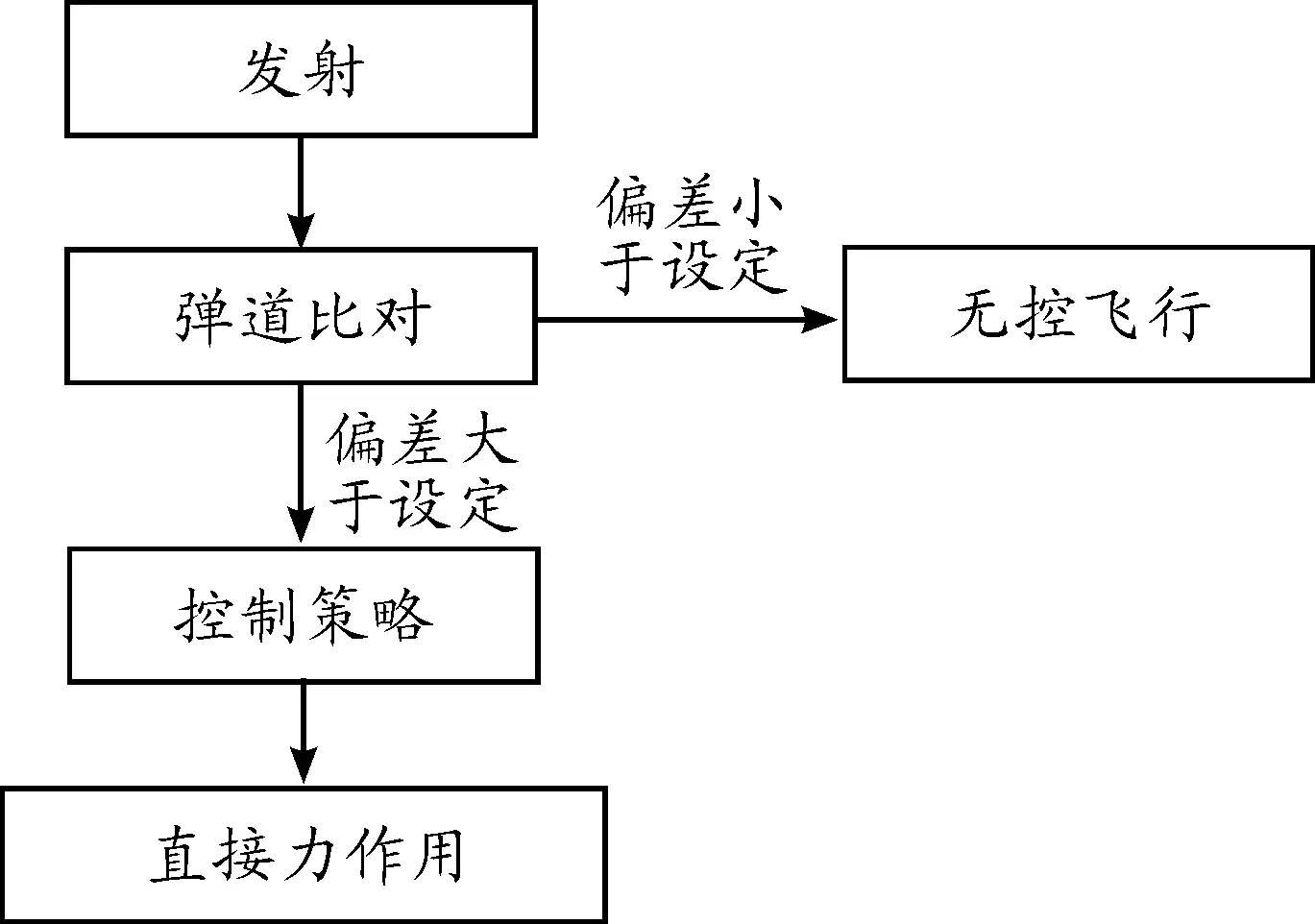
圖1 旋轉彈體工作時序與控制策略

脈沖機構安裝位置如圖2所示，設脈沖發動機距離彈體質心的距離為lj，每個噴管在彈體坐標系內的位置是固定的，脈沖力大小為Fp，它與Z1軸的夾角為λ(如圖3)。

圖2 彈體及修正機構位置示意圖

圖3 脈沖力大小及夾角示意圖

將脈沖力在彈體坐標系(OX1Y1Z1)中沿坐標軸分解，可以得到脈沖力及其對彈體質心產生的力矩分別為：

(1)

(2)

(3)

(4)

旋轉彈體飛行過程中彈體姿態不斷變化，為了定量描述平均作用效果，引入等效平均控制力。根據動量守恒原理，等效平均控制力和瞬時控制力在脈沖作用時間間隔內產生的沖量相等，設工作時間為t1，則有：

(5)

化簡可得直接力等效平均控制力如下：

(6)

1.3 控制系統模型

由于彈體內部空間限制，采用的脈沖機構沖量和個數有限，執行機構工作有離散式、有限次的特點，控制策略的設計轉化成為已知彈道初始條件及其彈道約束下，求滿足要求的最優脈沖機構修正控制參數，使其性能指標滿足最優條件的設計問題。采用最優控制理論方法，研究對象是一個以脈沖機構工作數量和落點誤差為優化目標的多目標優化問題?？蓪⒀芯繂栴}簡化為如下目標函數

(7)

式中:n′為工作的脈沖機構數量；n=20為脈沖機構總數；C′為目前系統的彈道偏差信息；C為系統設置的彈道偏差信息；k表示脈沖個數在優化算法中所占的比例系數；k取值范圍為大于0小于1的數。

2 粒子群優化算法

粒子群算法是一種基于群體的智能算法，它根據對環境的適應度將群體中的個體移動到好的區域，每次通過自身的飛行經驗和同伴的飛行經驗動態調整飛行速度，即通過兩個極值更新自己，一個極值是粒子本身找到的最優解，另一個極值是整個種群找到的最優解。采用粒子群優化算法驅動直接力裝置作用，優勢在于能夠精準確定起始時刻并依照彈體的位置信息確定需要起作用裝置的數量。

計算中以彈道偏差信息和直接力裝置工作數量為研究對象。假設將第i個粒子的位置和速度分別表示為：Xi=(Xi1,Xi2,…,XiD)和Vi=(Vi1,Vi2,…,ViD)，種群全局最優位置為Pg=(Pg1,Pg2,…,PgD)。粒子速度和位置更新為：

(8)

(9)

為了提高算法性能，本文采用粒子群優化算法，改進式(8)和式(9)：

(10)

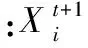
(11)

(12)

3 控制策略仿真分析

為了驗證所設計的基于粒子群優化算法的直接力工作策略，本研究基于旋轉導彈動力學和運動學模型，采用Matlab 軟件建立彈體六自由度模型，并編程仿真對比分析了3種不同工況的彈道落點誤差，分別是：① 無控狀態下的理論彈道信息；② 考慮側風干擾的彈道；③ 采用粒子群優化算法修正后的彈道。仿真計算參數和計算條件為：彈體質量為50 kg，發動機工作時間為1.2 s，轉速為15～20 r/s，發射角為45.8°，初始姿態角為45.8°，單個直接力等效作用力為1 900 N，作用時間為0.2 s，彈道落點誤差C小于50 m。計算結果如圖4所示。

圖4 不同工況彈道比較

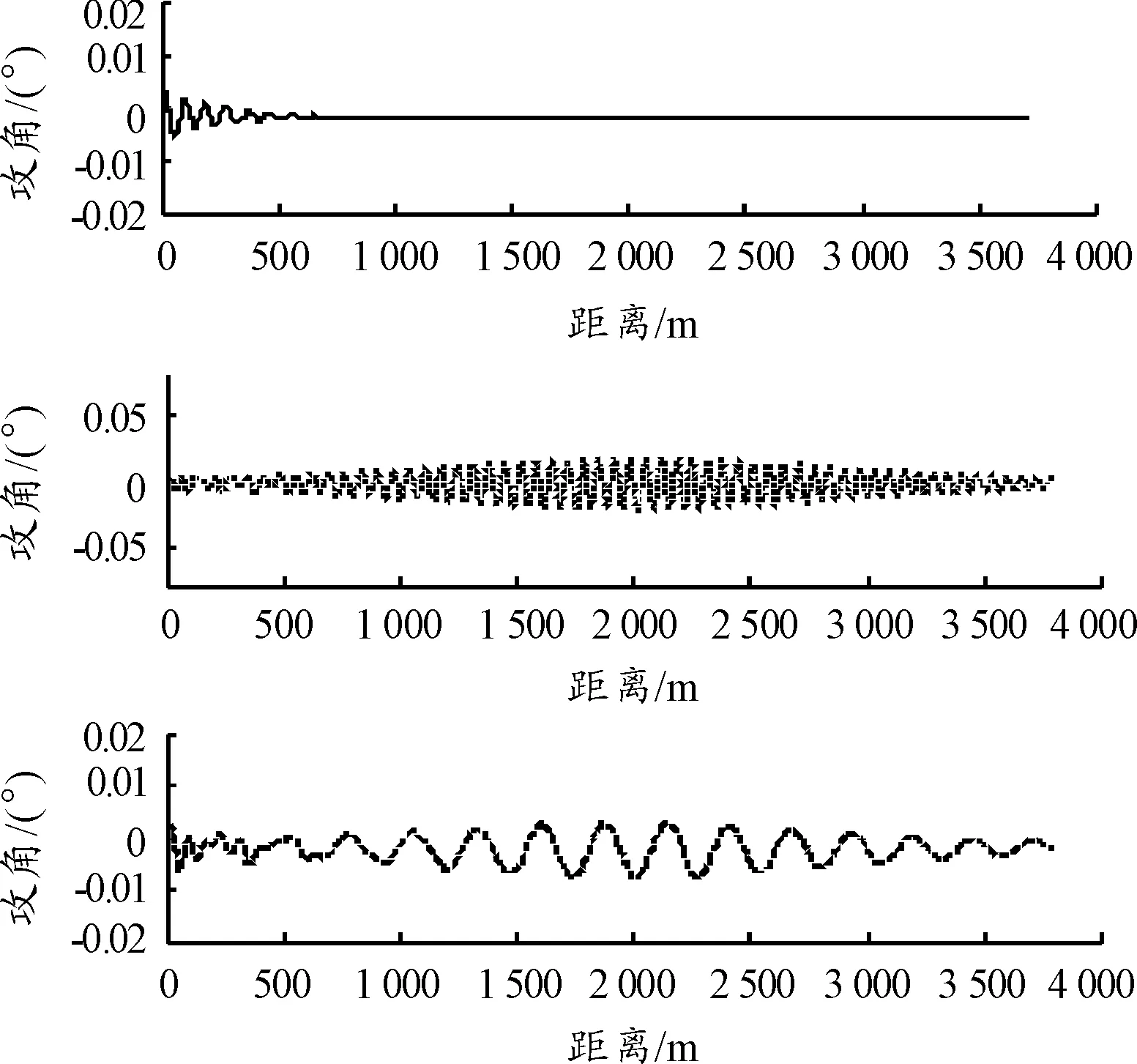
圖5 不同工況攻角比較

將修正彈道的仿真結果匯總列入表1。

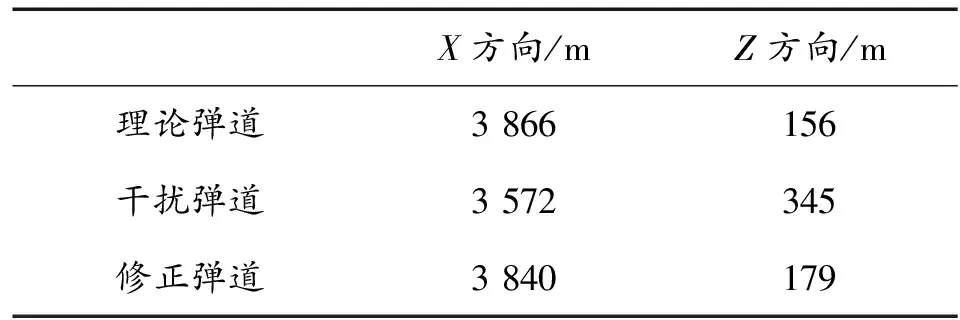
表1 彈道落點比較值(地面坐標系下)

通過仿真計算對比，在地面坐標系如果將理論彈道設為原點，則側風干擾條件下，彈道偏差值為X方向為294 m，Z方向為189 m，采用直接力裝置修正后的彈道偏差值為X方向26 m，Z方向為23 m。

4 結束語

通過彈體飛行過程中的攻角變化和落點誤差結果分析，表明基于粒子群優化算法的直接力修正能夠穩定彈體并減小落點誤差。本文研究工作驗證了所設計的控制算法的有效性，為旋轉導彈制導化改造的工程化應用提供了參考。

[1] 張明星，黃曉霞.國外遠程制導火箭彈技術現狀與趨勢[J].四川兵工學報，2013，34(7)：59-62.

[2] 李新國，方群.有翼導彈飛行動力學[M].西安:西北工業大學出版社，2005.

[3] 楊軍，楊晨，段朝陽,等.現代導彈制導控制系統設計[M].北京：航空工業出版社，2005.

[4] 李永亮.十字形鴨翼布局旋轉彈控制系統研究[D].南京:南京航空航天大學，2013.

[5] 郭正玉，梁曉庚.彈道修正彈模糊自適應PID控制器設計[J].四川兵工學報，2014，34(4)：1-4.

[6] 畢艷超，姚曉先，宋曉東，等.雙通道控制旋轉導彈的舵機控制研究[J].彈箭與制導學報，2014，34(2)：25-28.

[7] 鄭新，傅維賢，趙民.滾轉彈道導彈運動規律與控制研究綜述[J].航天控制，2011，32(4)：37-39.

[8] 任淼，王秀萍.國外空空導彈發展動態研究[J].航空兵器，2013，34(5)：1-4.

[9] 曹碩宏.基于柔性變結構控制理論的滾轉導彈飛行控制系統設計[D].南京:南京理工大學，2013.

[10]郭正玉，梁曉庚.制導火箭彈修正方法和控制精度分析[J].計算機仿真，2015，32(9)：91-94.

[11]PHILIPPE WERNERT.Stability analysis for canard guided dual-spin stabilized projectiles[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Chicago,Illinois,2009.

[12]ROGERS J,COSTELLO M.Design of a Roll-Stabilized Mortar Projectile with Reciprocating Canards[J].Journal of Guidance,Control,and Dynamics,2010,33(4):1026-1034.

(責任編輯周江川)

Research on Particle Swarm Optimization Control Method of Rotating Airframe Missile

ZHANG Hong1, GUO Zheng-yu2

(1.Military Representative Office of Heilongjiang, Harbin 150000, China; 2.China Airborne Academy, Luoyang 471000, China)

This paper, with a certain type of rotating airframe missile as the research object, according to the missile dynamics and kinematics model, formed a model of missile with direct force device, and simulated the effect of particle swarm optimization control method in ballistic characteristic point. Result shows that the way in the paper can reduce the circular error probable. The result provides reference for engineering application.

rolling airframe missile; direct force device; particle swarm optimization; simulation analysis

2016-07-05；

2016-08-25

航空科學基金(20140157002)

張泓(1977—)，男，碩士，主要從事軍事理論與科學、導彈控制系統設計理論研究; 郭正玉(1982—)，男，博士，主要從事導彈導航、制導與控制研究。

10.11809/scbgxb2017.01.008

張泓，郭正玉.基于粒子群優化算法的旋轉導彈姿態修正策略[J].兵器裝備工程學報，2017(1):32-35.

format:ZHANG Hong, GUO Zheng-yu.Research on Particle Swarm Optimization Control Method of Rotating Airframe Missile[J].Journal of Ordnance Equipment Engineering,2017(1):32-35.

TJ410.6

A