基于模態參數提取的隨機子空間辨識算法改進

李玉剛 葉慶衛 周 宇 方 寧寧波大學信息科學與工程學院，寧波,315211

基于模態參數提取的隨機子空間辨識算法改進

李玉剛 葉慶衛 周 宇 方 寧
寧波大學信息科學與工程學院，寧波,315211

隨機子空間辨識(SSI)算法在大型結構的振動檢測、損傷識別中有著重要的作用。引入稀疏優化取代最小二乘法來獲得盡可能稀疏的狀態矩陣，引入K-means算法從眾多模態參數中選出真實模態，以避免虛假模態的產生。實驗結果表明，所構建的稀疏改進SSI算法能準確提取模態參數，對工程應用具有較大的參考價值。

隨機子空間辨識算法；稀疏優化；最小二乘法：模態參數：K-means算法

0 引言

利用結構的動態響應識別結構損傷是近年來發展起來的結構損傷診斷新方法，而參數識別是結構健康監測領域中的重點。目前國內外模態參數的提取方法有頻域分解法[1]、PolyMax[2]、NexT[3]等，但是這些算法需要大量工作來確定具有最小量參數的模型，并進行迭代運算，往往存在發散或收斂緩慢等問題。隨機子空間識別算法 (stochastic subspace identification，SSI)[4]是基于隨機狀態空間模型的，只需要確定系統的階次，且由于算法中的奇異值分解，故該算法不存在收斂問題。

隨機子空間識別最關鍵的問題是確定系統階次，目前主要的兩種方法是奇異值跳躍法和穩定圖法。上述兩種方法的系統定階過程都需要人工參與，奇異值跳躍法需要人工找出奇異值跳躍點，受環境噪聲干擾較大；穩定圖法需要人工找出系統階次的范圍，受人的主觀判斷影響較大，很容易出現虛假模態現象。

稀疏表示[5-7]是一種高效的搜索算法，在壓縮感知中被廣泛地應用。在壓縮感知中，稀疏表示可以在不丟失原始信號信息的情況下，顯著減少觀測信號的次數，能有效實現信號的降維處理，具有很好的噪聲抗干擾能力。稀疏優化采用稀疏逼近來取代原始信號，從而顯著降低處理成本，特別對混合信號的分離有著顯著的效果。現階段的稀疏優化算法主要有梯度投影法[8]、匹配追蹤法[9]、正交匹配追蹤法(OMP)[10]等。

目前SSI算法能夠在系統低階情況下獲取較高精度的模態主頻參數和阻尼比，但是模態振型參數的提取還存在些許問題。另外SSI算法需要準確定階，且受噪聲的影響較大。本文在基于協方差的SSI方法(SSI-cov)[11-12]的基礎上用稀疏優化方法對其求狀態矩陣、輸出矩陣環節作了改進，用稀疏優化技術代替最小二乘法，并通過K-means算法來選擇系統模態，從而剔除系統虛假模態，減小系統階次對模態參數的影響，使模態參數更加精確。

1 基于協方差驅動的隨機子空間算法識別

在SSI-cov中，可以由采樣數據得到可觀矩陣Γ如下：

(1)

比較式(1)中兩式可得：

Γ2=Γ1Θ

(2)

其中，Θ是對角矩陣;C為系統輸出矩陣。然后通過最小二乘法求取狀態矩陣A。

現有SSI-cov算法首先需要確定系統階次，其系統定階的方法主要是奇異值(SVD)分解法[13]，可以得到較為準確的系統階次，但是當信號數據過大，外界環境產生的噪聲比較復雜時，在確定系統階次的時候往往會產生較大的偏差，很容易產生虛假模態。另外對輸出矩陣C的求解只計算了可觀矩陣Γ的第一行，可能會因為系統的復雜性而產生不可避免的偏差，導致結構模態振型出現紊亂。

2 SSI算法改進的稀疏求解

在現有的SSI-cov識別中，式(2)用最小二乘法求解狀態矩陣A，然后求解模態頻率ω*、阻尼比ξ*。這種方法對模型階次的限制較大，一旦模型階次確定不準確，虛假模態就會伴隨而生；在以往求取輸出矩陣C中，都是把可觀矩陣Γ的第一行作為C的固定值，然而當噪聲影響較大時，得到的C就會產生偏差，進而導致模態振型Ω*的求取精度出現較大的下降。

首先我們為模型階次nΔ賦一個較大的值，把可觀矩陣Γ轉化為

可得出狀態矩陣的等式方程：

ΓT=QTPT

(3)

對式(2)我們用高斯隨機測量矩陣H1進行觀測：

H1Γ2=H1Γ1Θ

(4)

將其轉化成稀疏等價模型：

(5)

這個優化問題是個NP難問題，DONOHO指出，當H1Γ1滿足RIP條件時，0范數的優化就可以轉化成1范數的優化問題，即

(6)

式中，σ1為誤差限度，是一個很小的正值。

對式(3)進行轉置并用高斯隨機測量矩陣H2觀測：

H2ΓT=H2QTPT

(7)

構建稀疏優化模型：

(8)

同樣，這也是一個NP難問題，當H2QT滿足RIP條件時，0范數的優化就可以轉化成1范數的優化問題：

(9)

式中，σ2為誤差限度，是一個很小的值。

經驗證，H1Γ1和H2QT能夠以很高的概率滿足RIP條件，符合稀疏求解的條件。但是我們通過式(6)和式(9)求取的稀疏解中有多于系統真實階次的非零解，這些較小的非零解屬于噪聲，不過稀疏解中的噪聲很小且極不穩定，通過多次運算可以很容易地統計找出，然后運用聚類的方法，對應得出真實模態參數，具體步驟如下。

(1)給系統的模型階次nΔ賦一個較大的值，選取合適的稀疏度k和誤差限度σ1、σ2。

(2)構建隨機高斯測量矩陣H1和H2，對式(6)用OMP方法進行稀疏求解，得到矩陣Θ，進而得到矩陣A，再對A進行特征值分解，得到特征值D；得到A之后，構建QT矩陣，然后對式(9)用OMP進行稀疏求解，得到矩陣PT，觀察PT的特點，就可以很容易地得到C。

(3) 由求得的A和C計算含有虛假模態的頻率向量ω*、阻尼比向量ξ*和模態振型Ω*。

(4)重復步驟N次，統計結果，得到最終的D*和C*，統計步驟如下：①對于步驟(2)，我們得到N個D和C，對每一個D和C求其均值，然后把D與C的元素的絕對值與其各自的均值比較，小于均值的強制置零，然后對照N個D在相同位置的非零個數，記為數組dD，同理，對照C在相同位置的非零個數，記為數組dC；②把數組dD和dC的元素與其均值相減，把差值數據的絕對值記為fD和fC，由K-means算法，我們把數組fD和fC任選兩個元素作為聚類中心，然后把剩下的元素與聚類中心比較，把離聚類中心較近的對象歸為一類，然后計算所獲得的新的聚類，不斷重復，直至標準測度函數開始收斂，然后我們統計出均值小的類的下標索引gD和gC；③把下標gD和gC對應的D和C值強制置零，然后得到最終的D*和C*。

(5)根據D*中非零元素的位置，從ω*、ξ*中選擇出系統模態ω、ξ；根據C*中非零元素的位置，從Ω*中選擇出模態振型Ω。

通過上述方法，如圖1所示，我們能夠把模型階次對模態參數提取的影響忽略不計，可以有效剔除虛假模態，并通過聚類的方法，很好地把噪聲剔除，較大程度地減小噪聲對結果的影響，從而提高算法的消噪能力和識別精度。

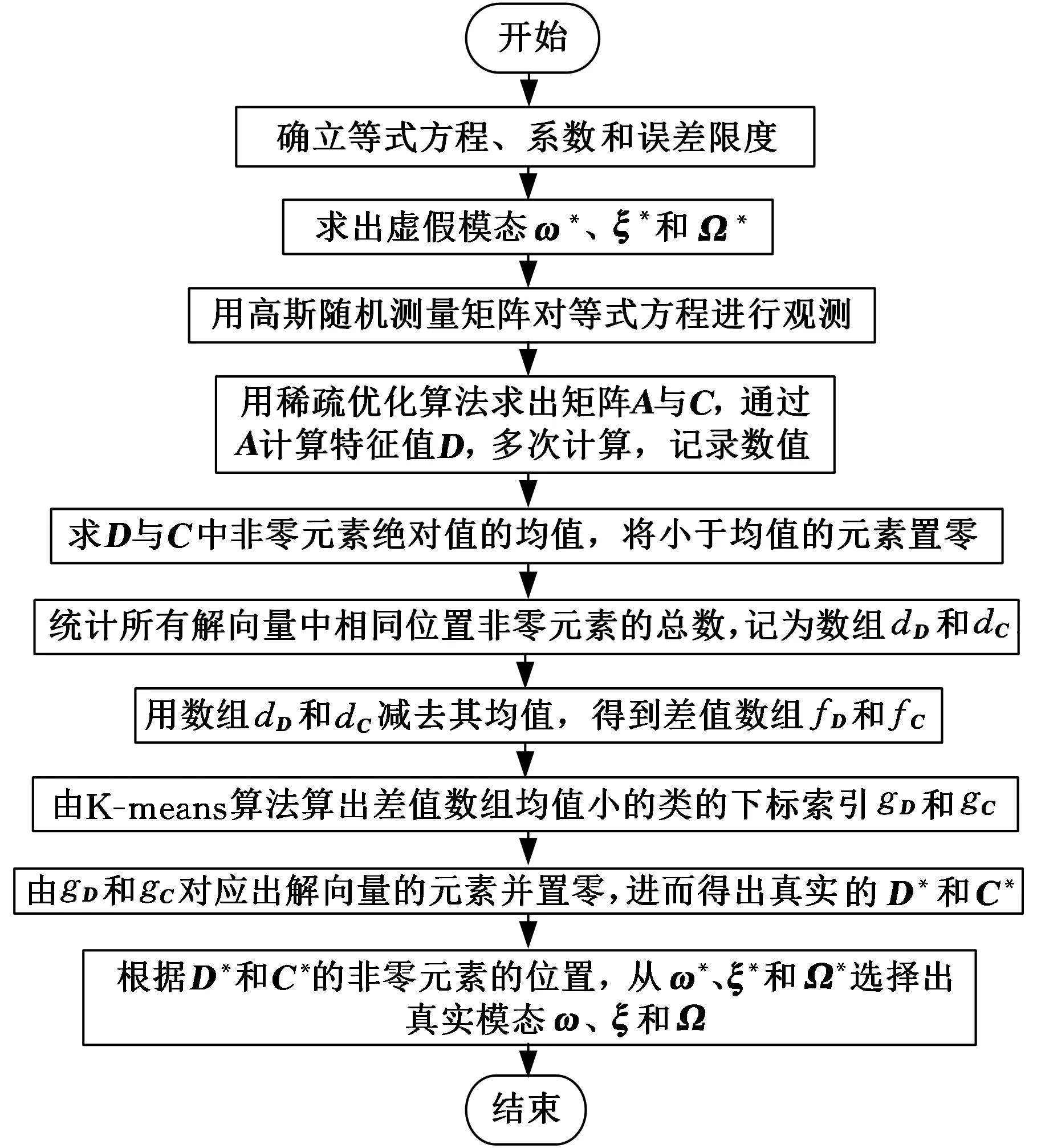
圖1 SSI算法改進稀疏求解Fig.1 Improvement and solution of SSI algorithm based on sparse representation

3 仿真實驗與分析

3.1 仿真實驗

本文以MATLAB 作為仿真工具，這里假設一個4次系統的仿真信號：

x=0.4e-0.012tcos(5.3t+0.25)+1.1e-0.057t·cos(3.9t+0.1)-1.3e-0.082tcos(6.6t+0.34)-0.8e-0.034tcos(4.4t+0.18)

(10)

由理論計算可得到系統的固有頻率ω、阻尼比ξ和模態振型系數Ω，如表1所示。

表1 系統固有模態參數
Tab.1 Inherent modal parameters of system

ω(Hz)ξ(N·S/m)Ω0.8440.0140.4000.6210.0921.1001.0510.078-1.3000.7010.049-0.800

對式(10)的仿真信號添加信噪比為5 dB的高斯白噪聲，以30 Hz的采樣頻率采集1000個采樣點，然后我們為系統階次n賦值80，然后計算頻率向量ω*、阻尼比向量ξ*、模態振型Ω*以及確立等式方程：

(Γ2)200×80=(Γ1)200×80Θ80×80

(11)

(12)

按照如下過程分步計算，最終可得到各階振型系數及模態。

(2)同樣地，構建高斯隨機測量矩陣(H2)24×200，對式(12)進行觀測，然后由式(9)得到矩陣C1×80。

(3) 重復步驟(1)8次，得到這8次計算的解集{A1,A2,…,A8}，計算特征解集{D1,D2,…,D8},對每一個特征值求取均值，然后將其元素的絕對值與其均值比較，小于均值的強制置零。然后對照8個特征值在相同位置的非零個數，記為數組dD。

(4) 重復步驟(2)8次，得到這8次計算的解集{C1,C2,…,C8},對每一個輸出矩陣求取均值，然后將其元素的絕對值與其均值比較，小于均值的強制置零。然后對照8個特征值在相同位置的非零個數，記為數組dC。

(5)將數組dD元素與其均值相減，差值數據的絕對值記為fD，由K-means算法統計出均值小的類的下標索引gD，排除下標索引gD之后，得出余下的下標2、7、24、37，從而求取特征值D*，通過D*就可以找出ω*和ξ*對應的位置。

(6) 將數組dC元素與其均值相減，差值數據的絕對值記為fC，由K-means算法我們統計出均值小的類的下標索引gC，排除下標索引gC之后，得出余下的下標3、13、25、42，從而求輸出矩陣C*，通過C*就可以找出對應的模態振型Ω*。

(7)步驟(5)與步驟(6)得出的D*、ω*、ξ*、C*、Ω*如表2所示。

表2 4階次系統的稀疏改進的模態參數
Tab.2 Modal parameters of sparse improvement based on 4 model order

D*ω*(Hz)ξ*(N·S/m)C*Ω*0.9950.8430.0131.5340.4320.9170.6240.0945.4621.1231.4841.0540.0800.948-1.3050.9340.7030.0510.859-0.812

通過表2，我們可以看出稀疏改進算法在模型階次過大和高斯白噪聲干擾的情況下，仍舊保證了很高的計算精度，很好地證明了稀疏改進算法的優越性。

3.2 模型階次對系統的影響

3.1節的稀疏求解具有一定的片面性，模型階次和稀疏度的選取較為主觀，所以為了使驗證結果更加準確，我們需要再次驗證。首先選用兩種差距比較明顯的較大模型階次，然后對每個模型階次下的稀疏度選取不同的值，以信噪比5 dB為干擾信號，各計算80次求均值，得到固有頻率見表3，阻尼比見表4，模態振型得到結果見表5。

表3 不同階次稀疏計算固有頻率Tab.3 Calculation of modal frequency of different order based on sparse algorithm Hz

表4 不同階次稀疏計算阻尼比Tab.4 Calculation of damping ratio of different order based on sparse algorithm N·S/m

表5 不同階次稀疏計算模態振型
Tab.5 Calculation of vibration pattem of different order based on sparse algorithm

階次稀疏度模態振型Ω1模態振型Ω2模態振型Ω3模態振型Ω450240.3981.098-1.295-0.79350480.4111.107-1.308-0.811100240.4031.104-1.302-0.803100480.4091.106-1.305-0.809

表3～表5顯示，兩種相差較大的模型階次計算結果基本一樣，且對稀疏度的敏感程度很低，這對我們稀疏度的選取提供了一個較大的范圍，因此，我們可以很容易地得出，稀疏改進算法對模型階次要求不高，可以很好地在剔除虛假模態的基礎上保持計算精度。

3.3 不同噪聲下的模態識別精度

為了更好地驗證稀疏改進算法的優越性，我們把稀疏改進算法與SSI-cov算法進行對比。

(13)

分別對信號添加不同的加性噪聲(脈沖噪聲和高斯白噪聲以及兩種噪聲的混合噪聲)，為了使結果更加精確，我們計算80次求其平均值，比較兩種算法在相同噪聲下對信噪比的敏感程度。因篇幅有限，這里只列舉4個比較典型的誤差對比。如圖2～圖5所示。

圖2 基于高斯白噪聲下頻率誤差對比Fig.2 Comparison of frequency error based on gauss white noise

圖3 基于混合噪聲下頻率誤差對比Fig.3 Comparison of frequency error based on mixed noise

圖4 基于高斯白噪聲下阻尼比誤差對比Fig.4 Comparison of damping ratio error based on gauss white noise

圖5 基于高斯白噪聲下模態振型誤差對比Fig.5 Comparison of vibration pattem error based on gauss white noise

從圖2中可以看出，在高斯白噪聲下，SSI-cov識別的頻率誤差起伏較大，在γSN為0～10 dB范圍內,波動特別明顯，可看出SSI-cov算法對噪聲較為敏感，而稀疏改進算法起伏波動比較平緩，有很高的穩定性；從圖3中可以看出，在混合噪聲下，SSI-cov識別的主頻精度比在高斯白噪聲下相對較差，對噪聲更加敏感，在信噪比15 dB以內，相對誤差變化起伏更大，而稀疏改進算法相對誤差變化平緩；從圖4中可以看出，SSI-cov識別的阻尼比在信噪比5 dB以內，已經產生了明顯的失真，當信噪比越小時，識別精度越差，而稀疏改進算法識別精度較高，表現出了很高的穩定性；從圖5中可以看出，稀疏改進算法的相對誤差始終在SSI-cov之下，特別當信噪比較小時，誤差值更為明顯。

4 實測信號分析

本文研究對象的工程數據采自寧波某斜拉索大橋。大橋全長67 m，由102根直徑為0.15 m的拉索構成拉索支撐系統。在采集過程中，采用WS-ZHT2振動設備和雙傳感器采集振動信號，雙傳感器安裝在拉索和梁端的鉸支部位，能有效感應索-梁耦合的拉索振動，如圖6所示。

圖6 傳感器安裝圖Fig.6 Sensors installation diagram

傳感器采集到的信號都是含噪信號，但是我們不知道噪聲的類型是否規則，不清楚無噪聲原始信號的波形，只清楚采集到的信號波形。這里我們以第6號到第12號斜拉索的振動采集信號為例，因篇幅有限，只顯示第10號斜拉索的振動波形圖，如圖7所示，信號具有較強的環境干擾，從而對模態參數提取的精度和噪聲抗干擾性要求較高。用本文算法對采集到的信號提取基頻參數，與SSI-cov算法作比較，來進一步驗證稀疏改進SSI算法的優越性。

圖7 第10號斜拉索振動波形圖Fig.7 Vibration waveform of No.10 stay cable

在圖7所示波形圖的基礎上，兩種算法的測定結果(測定10次，求其均值)如表6所示。

表6 兩種識別算法對斜拉索基頻識別情況
Tab.6 Frequency identification of two algorithms for the stay cable

斜拉索號參考基頻(Hz)識別方法計算結構基頻(Hz)相對誤差A60.7528稀疏改進SSI-cov0.75800.76520.00520.0124A80.7863稀疏改進SSI-cov0.79660.80380.01030.0175A100.8011稀疏改進SSI-cov0.80920.81530.00810.0142A120.7932稀疏改進SSI-cov0.80060.80580.00740.0126

從表6中數據可以看出，稀疏改進算法識別具有更好的精確度，相對誤差普遍較小，更加接近參考基頻(大橋管理服務有限公司提供)。稀疏改進算法解決了SSI-cov當階次確定有偏差的情況下，識別精度不準確的問題，另外稀疏改進算法對噪聲不敏感，本身在稀疏優化的過程中，就已經具有了很好的消噪能力。因此，我們得出如下結論：稀疏改進算法對系統階次的要求不高，即使出現定階錯誤對結果影響也可忽略，以及具有很好的抗噪性，在較大的噪聲干擾下，仍然具有良好的識別精度。

5 結論

綜上所述，稀疏改進SSI算法具有工程可行性。相較于經典的SSI算法的最小二乘法，稀疏優化的OMP算法在有噪聲或噪聲較大時，能夠較好地提取狀態矩陣和輸出矩陣，準確提取模態參數，表現出更好的抗噪聲性能，魯棒性有明顯的提升；相較于經典的SSI算法的系統定階，稀疏改進SSI的聚類算法在系統階次方面幾乎不需要定階，有效地解決了因模型階次過高而產生的虛假模態問題，擴大了模型階次的選擇范圍。

在仿真實驗中，通過與SSI-cov算法的對比，很好地驗證了稀疏改進SSI算法的抗噪性以及解決模型階次過高產生的虛假模態的能力；對寧波某大橋的斜拉索的基頻測定，更加有力地證明了稀疏改進算法的優越性。因此，稀疏改進SSI算法具有一定的工程應用價值。

[1] BRINCKER R, ZHANG L, ANDERSEN P. Modal Identification from Ambient Responses Using Frequency Domain Decomposition [C]//18thIMAC. San Antorio. Texas,2000:65-630.[2] GUILLAUME P, VERBOVEN P, VANLANDUIT S. Frequency-domain Maximum Llikelihood Identification of Modal Parameters with Confidence Intervals [C]//In Proceedings of ISMA 23, the International Confere-nce on Noise and Vibration Engineering. Leuven, Belgium,1998:16-18.

[3] JAMES G H, CARNE T G, LAUFFER J P. The Natural Excitation Technique for Modal Parameter Extraction from Operating Structures [J]. Modal Analysis: Int. J. Analytical and Experimental Modal Analysis,1995,10(4):260-227.

[4] PEETERS B, ROECK G D. Reference-based Stochastic Subspace Identification for Output-only Modal Analysis [J].Mechanical Systems and Signal Processing,1999,13(6):855-878.

[5] DONOHO D L. Compressed Sensing [J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[6] 宋歡歡，葉慶衛，王曉東，等. 基于稀疏AR建模信號去噪研究與應用[J].振動與沖擊,2015,34(6):127-131. SONG Huanhuan, YE Qingwei, WANG Xiaodong, et al. Study and Application of Signal Denoising Based on Sparse AR Model[J]. Journal of Vibration and Shock,2015,34(6):127-131.

[7] HAUPT J, BAJWA W U, RABBAT M, et al. Compressed Sensing for Networked Data [J]. IEEE Signal Processing Magazine,2008,25(2):92-101.

[8] BLUMENSATH T, DAVIES M E. Gradient Pursuits [J]. IEEE Trans. on Signal Processing,2008,56(6):2370-2382.

[9] MALLAT S G, ZHANG Z. Matching Pursuits with Time-frequency Dictionaries [J]. IEEE Transactions on Signal Processing,1993,41(12):3397-3415.

[10] TROPP J. Greed Is Good: Algorithmic Results for Sparse Approximation [J]. IEEE Trans. on Information Theory,2004,50(10):2231-2242.

[11] BOONYAPINYO V, JANESUPASAEREE T. Data-driven Stochastic Subspace Identification of Flutter Derivatives of Bridge Decks [J].Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(12):784-799.

[12] 李永軍，馬立元，王天輝，等.協方差驅動子空間模態參數辨識方法改進分析[J].中國機械工程，2012,23(13):1533-1536. LI Yongjun, MA Liyuan, WANG Tianhui, et al. An Improvement on Subspace Modal Parameter Identification Algorithm Driven by Covariance [J]. China Mechanical Engineering,2012,23(13):1533-1536.

[13] 趙學智，葉邦彥.分量形成方式對奇異值分解信號處理效果的影響[J].上海交通大學學報,2011,45(3):368-374. ZHAO Xuezhi, YE Bangyan. The Influence of Formation Manner of Component on Signal Processing Effect of Singular Value Decomposition[J]. Journal of Shanghai Jiaotong University,2011,45(3):368-374.

[14] CANDES E J, TAO T. Decoding by Linear Programming[J].IEEE Transactions on Information Theory,2010,34(4):435-443.

[15] 張成，楊海蓉，韋穗.基于隨機間距稀疏Toeplitz測量矩陣的壓縮傳感[J].自動化學報，2012,38(8):1362-1369. ZHANG Cheng, YANG Hairong, WEI Hui. Compressive Sensing Based on Deterministic Spar-se Toeplitz Measurement Matrices with Random Pitch [J]. Acta Automatica Sinica,2012,38(8):1362-1369.

(編輯 袁興玲)

Improvement of SSI Algorithm Based on Extraction of Modal Parameters

LI Yugang YE Qingwei ZHOU Yu FANG Ning

Faculty of Information Science and Enginner，Ningbo University， Ningbo，Zhejiang,315211

SSI algorithm played an important role in the large structure vibration detection and damage identification. Sparse optimization solution was introduced to replace the least square method that was used to get sparser state matrix. K-means algorithm was introduced to elect real modal parameters from many modal parameters so as to eliminate the false modals effectively. The experimental results show that optimization solution of SSI algorithm may accurately extract modal parameters. The work herein has reference values in engineering applications.

stochastic subspace identification (SSI) algorithm; sparse optimization; least square method; modal parameter; K-means algorithm

2016-07-20

國家自然科學基金資助項目(51675286，61071198)；浙江省自然科學基金資助項目(LY13F010015)；寧波市自然科學基金資助項目(2012A610019)；浙江省科技創新團隊資助項目(2013TD21)

TP391.4

10.3969/j.issn.1004-132X.2017.01.012

李玉剛，男，1991年生。寧波大學信息科學與工程學院碩士研究生。主要研究方向為振動信號處理。E-mail:630818644@qq.com。葉慶衛，男，1970年生。寧波大學信息科學與工程學院副教授。周 宇，男，1962年生。寧波大學信息科學與工程學院教授。方 寧，1992年生。寧波大學信息科學與工程學院碩士研究生。