軌道交通線網常乘客比例分析

鮑 楓，汪 波,3，黃建玲，何志瑩

（1.北京市交通信息中心，北京市 1 00161；2.綜合交通運行監測與服務北京市重點實驗室，北京市 1 00161；3.北京市交通委員會，北京市 1 00161）

軌道交通線網常乘客比例分析

鮑 楓1,2，汪 波1,2,3，黃建玲1,2，何志瑩1,2

（1.北京市交通信息中心，北京市 1 00161；2.綜合交通運行監測與服務北京市重點實驗室，北京市 1 00161；3.北京市交通委員會，北京市 1 00161）

根據城市軌道交通常乘客比例數據的節假日特點，在消除常乘客比例數據的趨勢項的時候，引入表示節假日特征的虛擬變量，量化節假日因素對常乘客比例的影響，建立常乘客比例數據與時間、具有節假日特征的虛擬變量之間的回歸模型,達到同時消除趨勢項和節假日特征的影響的目的，掌握節假日對常乘客比例的影響規律。通過自相關和偏自相關函數對消除趨勢項和節假日因素的數據序列進行平穩性和周期性分析，消除周期性特征影響。最后，構建基于虛擬變量線性回歸和季節ARIMA的組合預測模型，修正了原有的季節ARIMA。以2015年3月2日到2016年3月27日之間56周的北京軌道交通日常乘客比例數據進行實例驗證，表明本文構建的組合預測模型的精度高于原有的季節ARIMA模型。

軌道交通；常乘客比例；虛擬變量；回歸模型；修正季節ARIMA模型

0 引 言

城市軌道交通具有大容量、快速準點、安全高效等優點，近年來客流量增長迅猛，使得軌道交通面臨著嚴重的擁擠問題，這給有關部門的運營組織管理工作提出了新的課題。魯放等[1]提出軌道交通常乘客的概念，定義為“經常乘坐城市軌道交通出行，并熟練使用城市軌道交通，而且具備一定出行習慣的乘客”。常乘客的比例會受到假期、季節等因素的影響。本文以城市軌道交通一卡通使用量比例表征軌道交通線網常乘客比例，建立軌道交通線網常乘客比例預測模型，研究常乘客的比例變化趨勢，為軌道交通運營組織提供參考，提升軌道交通運輸服務水平。

統計期內的軌道交通常乘客比例是按照時間順序取得的一系列軌道交通常乘客比例觀測值。這些觀測值形成時間序列。基于時間序列的預測理論的基本思想是時間序列的任一時刻的值與其前期數據相關。通過建立這種相關關系的模型在歷史數據的基礎上預測將來的未知數據[2-4]。現實中的數據很多是非平穩的時間序列，如股價序列、氣候變化等，George E.P.Box和 Gwilym M.Jenkins提出自回歸整合滑動平均模型(ARIMA)能解決非平穩時間序列的處理問題。

在這種非平穩的時間序列中，有些序列存在明顯的周期性變化。這種周期是由于季節性變化（包括季度、月度、周度等變化）或其他一些固有因素引起的。這類序列稱為季節性序列，如季度時間序列、月度時間序列、周度時間序列等。處理季節性時間序列只用以上介紹的方法是不夠的。描述這類序列的模型之一是季節時間序列模型(seasonal ARIMA model)用SARIMA表示，較早文獻也稱其為乘積季節模型（multiplicative seasonal model）。居民季度用煤消耗量、某地區的月降水量、居民日用水量、軌道交通日客運量、軌道交通日常乘客比例等屬于季節性時間序列。國內已經有很多文獻探討了季節ARIMA模型在各行業的應用[5-8]。蔡昌俊等[9]基于城市軌道交通自動售檢票系統采集的進出站客流的歷史數據，構建了乘積ARIMA模型，實現對進出站客流量的精確預測；何九冉[10]構建了城市軌道交通某運營線路平常日客流預測ARIMA-RBF組合模型。

除了利用ARIMA模型及組合模型研究軌道交通客流規律，李春曉等[11]提出一種基于廣義動態模糊神經網絡（GD-FNN）的短時進站客流量預測方法，預測軌道交通車站每日分時進站量；王玉萍等[12]提出了包含可信度分析、客流特性分析、風險性分析和敏感性分析在內的城市軌道交通客流預測結果分析的結構體系；郝勇[13]構建了周客流日均量的回歸模型，測算上海地鐵周客流日均量趨勢值；徐瑞華等[14]研究了城市軌道交通線路客流分布的實時預測方法。但是在目前的研究中，時間序列的取值會受到節假日，例如元旦、春節、五一等的影響，如果只是使用差分方法，去除不了節假日的影響。

基于以上現狀，本文通過分析2015年3月2日到2016年3月27日之間56周的北京軌道交通日常乘客比例數據，引入表示節假日特征的虛擬變量，通過建立回歸方程的形式，去除趨勢項和節假日影響因素，建立城市軌道交通常乘客比例修正季節ARIMA模型，掌握常乘客比例隨日期及節假日變化的規律，預測短期內常乘客比例。

1 修正季節ARIMA模型構建

一般季節ARIMA模型通過逐步消除趨勢項、季節項，然后對得到的平穩序列建立ARMA預測模型。但是在日時間序列數據中，數據值還會受到節假日的影響，例如元旦、春節、五一等，通過傳統的差分方法消除不了節假日的影響。本文提出引入表示節假日特征的虛擬變量，建立基于虛擬變量的線性回歸模型來消除趨勢項和節假日的影響，對來消除趨勢項和節假日的影響之后的序列再構建季節ARIMA模型，最后得到基于虛擬變量線性回歸和季節ARIMA的組合預測模型，對原有的季節ARIMA模型進行修正。這種方法不需要人為的事先去除節假日的數據，避免了缺失信息的產生，保證了數據信息的連續性，同時有利于掌握節假日對常乘客比例的影響規律。具體步驟：

第一步：建立城市軌道交通常乘客比例數據與連續變量和具有節假日特征的虛擬變量的回歸模型，見式（1）：

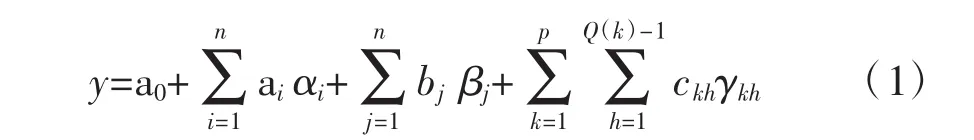
式中：y為城市軌道交通常乘客比例數據；a0為常數項；αi為第i個連續變量；ai為第i個連續變量的系數；n為連續變量的個數；βj為第j個節假日特征有序虛擬變量；bj為第j個節假日特征有序虛擬變量的系數；m為節假日特征有序虛擬變量的個數；γkh為第k個節假日特征無序虛擬變量的第h個啞元變量，如果某一節假日特征取值有Q（k）種情況，并且是無序的，應引入Q（k)-1個表示這一特征的啞元變量；ckh為第k個節假日特征無序虛擬變量的第h個啞元變量的系數；Q（k）為第k個節假日特征無序虛擬變量的取值個數；P為節假日特征無序虛擬變量的個數。

第二步：進行m個節假日特征有序虛擬變量與p個節假日無序特征變量（γ11，γ12，…，γ1，Q(1)-1），（γ21，γ22，…，γ2,Q(2)-1）…，（γp1，γp2，…，γp,Q(p）-1）相互之間相關關系的檢驗，得到分別獨立的節假日特征虛擬變量的組合。

第三步：y分別與第二步得到的獨立的節假日特征虛擬變量的組合建立回歸方程，應用最小二乘法得到參數組合，根據t檢驗、修正的R2、AIC、SC等檢驗規則，確定最優回歸方程，從而確定a0、ai、bj、ckh等系數的估計值、、、，并對y進行預測，得到y的預測值，見式（2）：

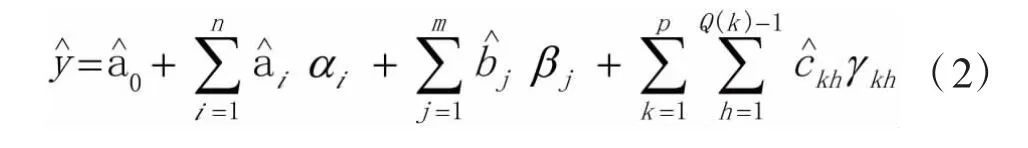
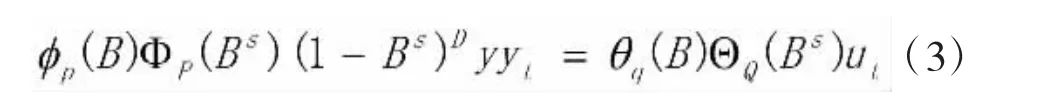
式中：P為季節自回歸階數；Q為季節移動平均階數；ΦP（BS）為季節P階自回歸算子；ΘQ（BS）為Q階移動平均算子。

第五步：結合式（2）和式（3），建立城市軌道交通常乘客比例數據組合預測模型，見式（4）：

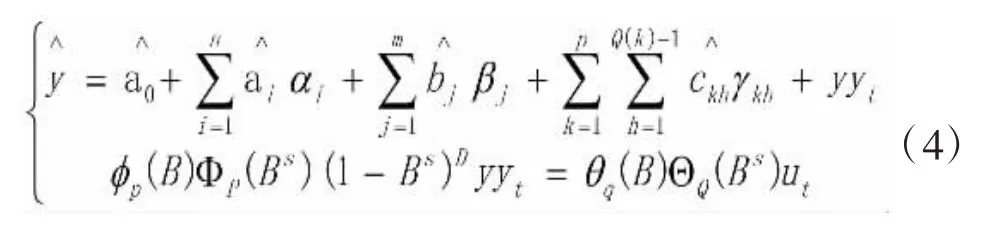
2 實例驗證

本節中，使用季節ARIMA方法（方法一）及修正后的基于虛擬變量線性回歸和季節ARIMA的組合預測模型（方法二，式（4））對城市軌道交通常乘客比例數據進行建模，并對比兩種方法的精確度，數據時間段為2015年3月2日到2016年3月27日之間56周的北京城市軌道交通常乘客比例數據，共392個數據。

2.1 季節ARIMA方法（方法一）

根據北京城市軌道交通常乘客比例數據的特征，建立ARIMA(2,1,3)(1,1,1)7的模型。模型展開式見式（5）：

利用式（5）預測2016年3月28日至4月4日（4月2日至4月4日為清明節假期）的日常乘客比例，結果見表1。

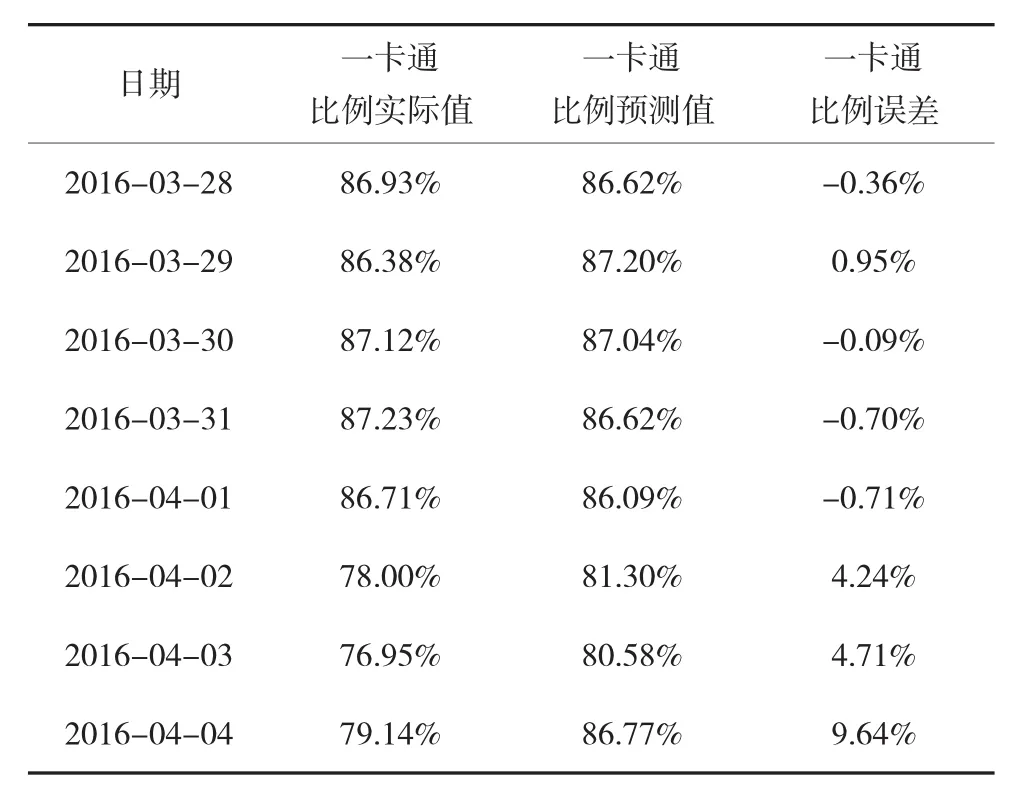
表1 方法一預測結果及誤差

2.2 基于虛擬變量線性回歸和季節ARIMA的組合預測模型（方法二，修正季節ARIMA模型）

2.2.1 模型建立

按照第1節描述的方法進行建模，引入表征節假日特征的有序和無序虛擬變量：

（1）表征節假日長短的虛擬變量β1：此虛擬變量為有序分類變量，所以取值用0，1，2來表示。0表示非節假日；1表示長度為3天的節假日，例如元旦、清明、五一、端午、元宵節；2表示長度為7天的節假日，例如春節、十一。

（2）表征節假日的回家、旅游特征變量γ11，γ12:此變量為無序變量，特征取值為回家、旅游及非節假日，所以需生成兩個啞變量γ11，γ12。在我國節假日中，春節、清明一般外地人回老家比較多，賦值為γ11=1，γ12=0；其他節假日旅游特征賦值為γ11=0，γ12=1；非節假日賦值為γ11=0，γ12=0。

（3）表征不同節假日的虛擬變量：每年節假日有7種，分別為元旦、春節、清明、五一、端午、元宵節、十一，但是有時會因為一些原因增加放假日期，例如2015年9月3日至5日調休放假，形成3天小長假，所以認為節假日有8種,分別為元旦、春節、清明、五一、端午、中秋節、十一、其他，再加上還需賦值非節假日，所以節假日種類有9種。節假日為無序變量，量化時需派生出8個啞變量，取值見表2。

根據修正的決定系數（Adjusted R2）、AIC、SC等檢驗規則，表征節假日長短虛擬變量β1與城市軌道交通常乘客比例時間序列數據建立回歸方程為最優方案。回歸方程為式（6）：

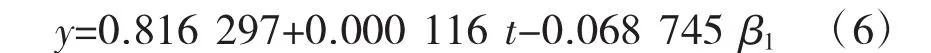
從式（6）可得出：節假日的長短對軌道交通日常乘客比例數據有明顯的影響，長度為7天的節假日常乘客比例值平均比長度為3天的節假日常乘客比例值低0.069左右。

記利用式（6）消除趨勢項和節假日影響后的數據序列為yy，對yy建立ARIMA（2,0,3）（1,1,1）7的模型。

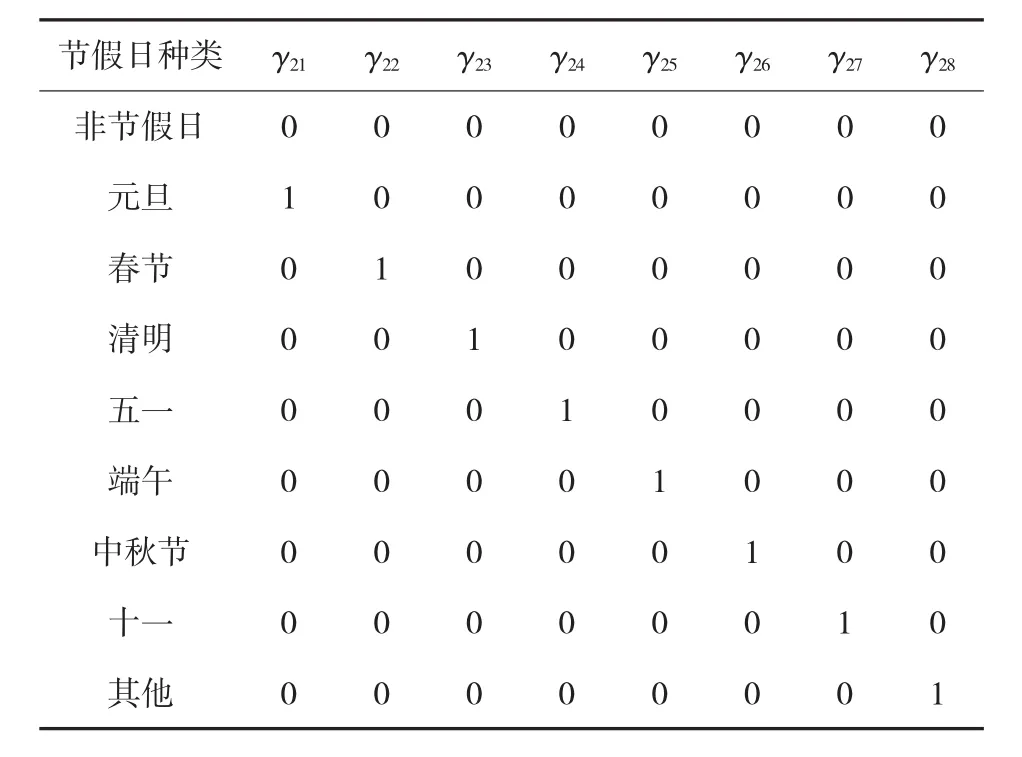
表2 節假日變量賦值

所以修正后的軌道交通常乘客比例數據y的組合預測模型為式（7）：

2.2.2預測

利用式（7）預測2016年3月28日至4月4日（4月2日至4月4日為清明節假期）的日常乘客比例，結果見表3。

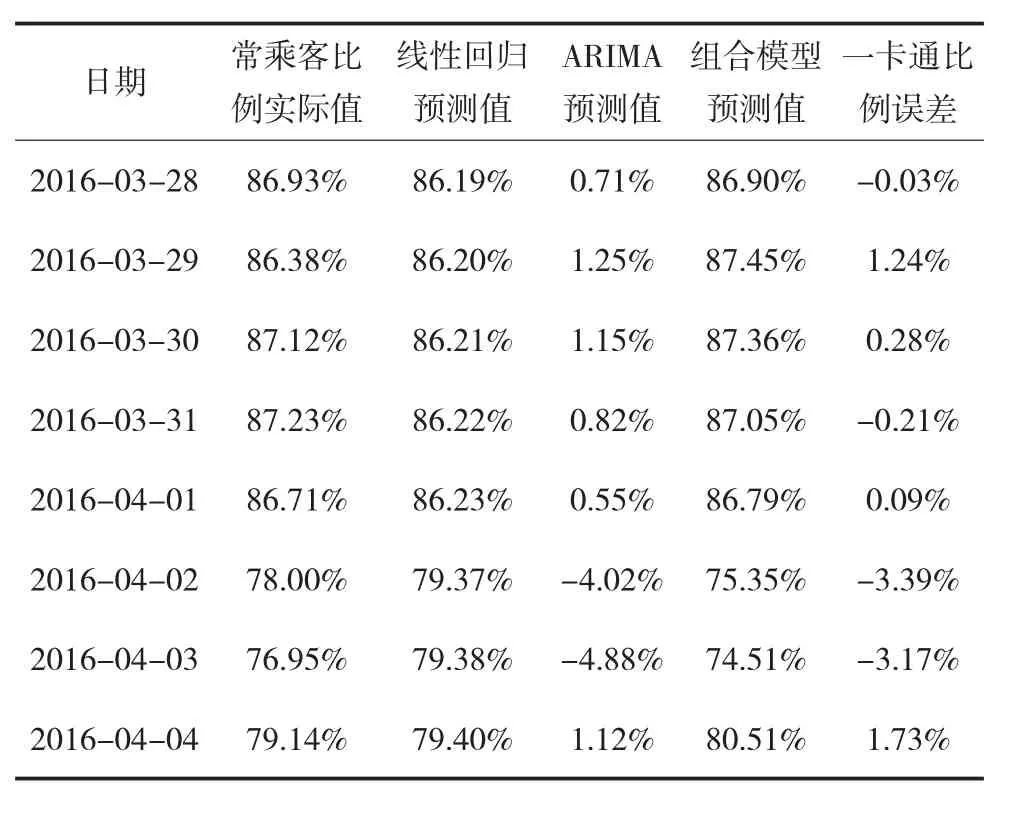
表3 方法二預測結果及誤差

2.2.3對比分析

對比表2和表3兩種方法的誤差，表2（方法一）的平均誤差為2.68%，表3（方法二）的平均誤差為1.26%，可見方法二的精度高于方法一，并且在節假日（4月2日至4月4日為清明節假期）的預測上，精度明顯高于方法一。所以本文構建的基于虛擬變量線性回歸和季節ARIMA的組合預測模型（式7），達到了對原有的季節ARIMA的修正效果。

3 結 論

本文依據2015年3月2日至2016年3月27日常乘客比例數據分別建立了常乘客比例ARIMA季節模型以及基于虛擬變量線性回歸和季節ARIMA的組合預測模型，對比了兩種方法的預測精度，得出以下結論：

（1）基于虛擬變量線性回歸和季節ARIMA的組合預測模型的精度高于原有的季節ARIMA的預測模型；

（2）常乘客比例數據具有緩慢遞增的趨勢和周期為7天的季節性趨勢，且遞增趨勢明顯弱于季節性趨勢；

（3）節假日的長短對軌道交通日常乘客比例數據有明顯的影響，長度為7天的節假日常乘客比例值平均比長度為3天的節假日常乘客比例值低0.069左右；

（4）模型的參數并不是越多越好，在滿足殘差序列具有較高的白噪聲檢驗的相伴概率（p-Q）情況下，可進行多個模型的比較，綜合考慮Adjusted R2、AIC、SC等檢驗方法，選擇最優模型。

基于本文建立的組合預測模型，可以預測近期城市軌道交通路網常乘客比例，掌握?？碗S時間變化的趨勢，為軌道交通運營管理部門提前做好運營組織、運營計劃提供量化的參考依據。

[1]魯放，韓寶明，蔡曉春.城市軌道交通常乘客行為研究[J].城市軌道交通研究，2012（2）：39-42.

[2]G.E.P.Box，G.M.Jenkins，G.C.Reinsel.時間序列分析：預測與控制[M].北京：中國統計出版社，1999．

[3]安鴻志，陳兆國，杜金觀，等.時間序列的分析與應用[M]．北京:科學出版社，1983.

[4]楊叔子，吳雅，軒建平，等．時間序列分析的工程應用[M]．武漢：華中科技大學出版社，2007．

[5]孫彩云，楊曉靜.乘積ARIMA模型的建立與應用[J].華北科技學院學報，2008，5(2)：85-89.

[6]李勇，吳寶亮，楊秀苔，等.基于乘積ARIMA模型的產品不確定性需求預測[J].系統工程與電子技術，2005，27(1)：60-62.

[7]湯巖，王福林，王吉權.基于季節ARIMA模型的電力系統負荷短期預測[J].數學的實踐與認識，2012，42(10)：74-80.

[8]童明榮，薛恒新，林琳.基于季節ARIMA模型的公路交通量預測[J].公路交通科技，2008，25(1)：124-128.

[9]蔡昌俊，姚恩建，王梅英，等.基于乘積ARIMA模型的城市軌道交通進出站客流量預測 [J].北京交通大學學報，2014，38(2)：135-140.

[10]何九冉.城市軌道交通客流統計特征分析及組合預測方法實證研究[D].北京：北京交通大學，2013.

[11]李春曉，李海鷹，蔣熙，等.基于廣義動態模糊神經網絡的短時車站進站客流量預測[J].都市快軌交通，2015，28(4)：57-61.

[12]王玉萍,陳寬民,楊富社，等.城市軌道交通客流預測結果的技術分析體系 [J].長安大學學報：自然科學版，2011，31(3)：72-79.

[13]郝勇.上海地鐵周客流量的數值分析與預測 [J].上海工程技術大學學報，2010，24(1)：60-65.

[14]徐瑞華，徐永實.城市軌道交通線路客流分布的實時預測方法[J].同濟大學學報：自然科學版，2011，39(6)：857-861.

U121

A

1009-7716（2017）01-0129-04

10.16799/j.cnki.csdqyfh.2017.01.038

2016-10-31

鮑楓（1976-），女，河南安陽人，副研究員，從事交通信息化研究.