N(2,2,0)代數的(∈δ,∈δ∨qδ(λ,μ))-模糊理想*

傅小波，廖祖華

1.無錫職業技術學院，江蘇 無錫 214121

2.江南大學 理學院，江蘇 無錫 214122

N(2,2,0)代數的(∈δ,∈δ∨qδ(λ,μ))-模糊理想*

傅小波1，廖祖華2+

1.無錫職業技術學院，江蘇 無錫 214121

2.江南大學 理學院，江蘇 無錫 214122

將模糊點和模糊集間的“∈（屬于）”和“q(λ,μ)（廣義重于）”關系推廣為“∈δ（Ω-屬于）”和“（Ω-重于）”關系，提出了-模糊代數。將-模糊代數與N(2,2,0)代數相結合，給出了點態化-模糊理想和Ω(λ,μ)-模糊理想的概念，證明了兩者之間的等價關系，研究了它們的一些基本性質；最后提出了點態化-模糊子代數和Ω(λ,μ)-模糊子代數的定義，研究了-模糊理想和-模糊子代數的相互關系。

N(2,2,0)代數；-模糊理想；-模糊子代數

1 引言

非經典數理邏輯理論是處理不確定性信息的有力工具。近年來，越來越多的學者運用代數學的相關理論研究非經典邏輯。1996年，鄧方安、徐揚從代數學的角度對fuzzy蘊涵代數[1]的蘊涵算子做進一步抽象，提出了N(2,2,0)代數[2]；隨后，眾多學者對N(2,2,0)代數的相關理論做了大量的研究，獲得了許多有意義的結果[3-7]。

1965年，美國控制論專家Zadeh創立了模糊集理論[8]，隨后模糊集的思想和理論引起了眾多學者的關注，并被廣泛地應用于各個領域；1980年，劉應明在文獻[9-10]中給出了模糊點和模糊集間的“∈（屬于）”和“q（重于）”關系，極大地促進了模糊集理論的發展；1992年，Bhakat和Das利用“∈（屬于）”和“q（重于）”關系，在文獻[11]中定義了(∈,∈∨q)-模糊子群。2012年，廖祖華等人將“q（重于）”關系推廣為“q(λ,μ)（廣義重于）”關系，在文獻[12]中引入了(∈,∈∨q(λ,μ))-模糊代數，豐富了模糊集理論，并獲得了許多有意義的結果[13-15]。

2001年，Young等人在文獻[16]中提出了Ω-模糊集，并將其與BCK/BCI代數相結合，給出BCK/BCI代數的Ω-模糊理想的概念。2005年，詹建明等人提出了BCK/BCI代數的Ω-模糊點理想的概念，進一步促進了Ω-模糊集的發展[17]。隨后，彭家寅對Ω-模糊集做了進一步的研究，給出了BCI代數的Ω-模糊p-理想、BCI代數的Ω-模糊H-理想、BCH代數的Ω-模糊正定關聯理想、BCH代數的Ω-模糊點理想等概念[18-21]；2013年，廖祖華等人將Ω-模糊集與群和環相結合，并對相關的性質進行了研究，獲得了許多有意義的結果[22-25]。同時，劉衛鋒將Ω-模糊集應用于布爾代數，給出了Ω-模糊子代數的概念[26]。2015年，湯華晶將Ω-模糊集與軟集理論相結合，提出了Ω-模糊軟環的概念[27]。

本文在上述工作的基礎上，給定一個集合Ω，提出了模糊點和模糊集間的“∈δ（Ω-屬于）”和“（Ω-重于）”關系。若模糊點和模糊集間具有“∈δ（Ω-屬于）”和“（Ω-重于）”關系的代數結構，稱之為(∈δ,∈δ∨)-模糊代數。由定義8及例3可知：若令A(x,δ)=A′(x)，則模糊點和模糊集間的“∈δ（Ω-屬于）”是“∈（屬于）”，“（Ω-重于）”是“（廣義重于）”，此時，(∈δ,∈δ∨)-模糊代數是(∈,∈∨q(λ,μ))-模糊代數。在一般情況下，(∈δ,∈δ∨)-模糊代數不一定是(∈,∈∨q(λ,μ))-模糊代數。因此，(∈δ,∈δ∨)-模糊代數是一種新的代數結構。本文將(∈δ,∈δ∨)-模糊代數與N(2,2,0)代數相結合，給出了點態化的(∈δ,∈δ∨)-模糊理想和(∈δ,∈δ∨)-模糊子代數的概念，并討論了其相關性質。

2 預備知識

定義1[2]設S是含有常元0的集合，在S中定義二元運算*和Δ，如果?x,y,z∈S，滿足下列條件：

（1）x?(yΔz)=z?(x?y)

（2）(xΔy)?z=y?(x?z)

（3）0?x=x

則稱(S,?,Δ,0)是一個N(2,2,0)代數，簡稱S是一個N(2,2,0)代數。

若(S,?,Δ,0)是一個N(2,2,0)代數，則(S,?)和(S,Δ)都是半群，因此N(2,2,0)代數是帶有一對對偶半群的雙半群；若將定義1中的條件（3）0?x=x，加強為0?x=x=x?0，則(S,?,Δ,0)代數是一個交換幺半群，且?=Δ。

例1設S={0,1}，S上的運算*和Δ的定義如表1、表2，則S={0,1}是一個N(2,2,0)代數[2]，同時也是一個交換幺半群。

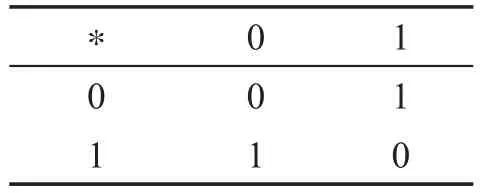
Table 1 Operator“*”表1 運算“?”

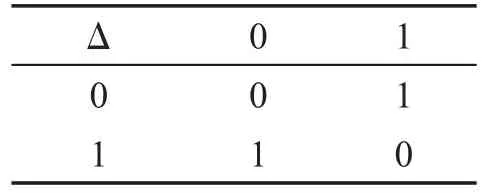
Table 2 Operator“Δ”表2 運算“Δ”

一般情況下，若(S,?,Δ,0)是一個N(2,2,0)代數，且?≠Δ，則(S,?,Δ,0)不一定是交換幺半群。

例2設S={0,a,b}，S上的運算?和Δ的定義如表3、表4，則S={0,a,b}是一個N(2,2,0)代數[3]，但不是交換幺半群。

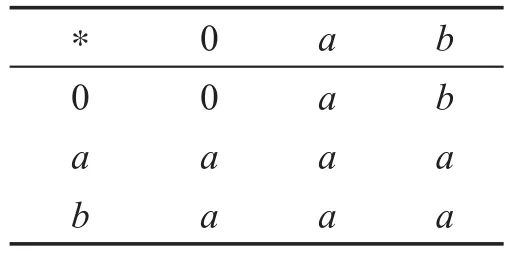
Table 3 Operator“*”表3 運算“?”

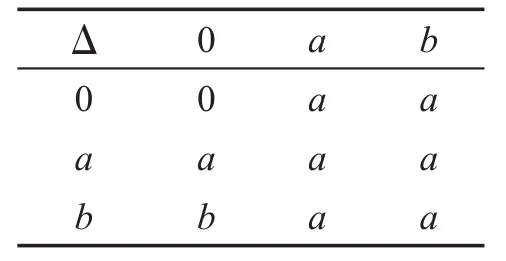
Table 4 Operator“Δ”表4 運算“Δ”

引理1[2]若S是一個N(2,2,0)代數，則?x,y,z∈S，恒有下列等式成立：

（1）x?y=yΔx；

（2）x?(y?z)=y?(x?z)，(xΔy)Δz=(xΔz)Δy；

（3）(x?y)?z=x?(y?z)，(xΔy)Δz=xΔ(yΔz)。

定義2[3]Q是S的子集，稱Q是S上的一個理想，如果滿足下列條件：

（1）0∈Q；

（2）?x∈Q，若x?y∈Q，則y∈Q。

定義3[15]Q是S的子集，稱Q是S上的一個子代數，如果滿足下列條件：

（1）0∈Q；

（2）?x,y∈Q，有x?y∈Q且yΔx∈Q。

定義4[15]設A是S上的一個模糊子集，稱A是S廣義模糊N(2,2,0)子代數，如果?x,y∈S，滿足下列條件：

（1）A(0)∨λ≥A(x)∧μ；

（2）A(x?y)∨λ≥A(x)∧A(y)∧μ；

（3）A(xΔy)∨λ≥A(x)∧A(y)∧μ。

定義5[15]設A是S上的一個模糊子集，稱A是S的(∈,∈∨q(λ,μ))-模糊N(2,2,0)子代數，如果?t,r∈(λ,1]及?x,y∈S，則有：

（1）若xt∈A，則0t∈∨q(λ,μ)A；

（2）若xt∈A且yr∈A，則(x?y)t∧r∈∨q(λ,μ)A；

（3）若xt∈A且yr∈A，則(xΔy)t∧r∈∨q(λ,μ)A。

引理2[15]A是S的(∈,∈∨q(λ,μ))-模糊N(2,2,0)子代數?A是S的(λ,μ)-模糊N(2,2,0)子代數。

定義6[12]設t,λ,μ∈[0,1]且λ〈μ，A是S上的一個模糊集，若A(x)≥t，則稱xt屬于A，記作xt∈A；若λ〈t且A(x)+t＞2μ，則稱xt廣義重于A，記作xtq(λ,μ)A；若xt∈A或者xtq(λ,μ)A，則記作xt∈∨q(λ,μ)A。

本文從現在開始恒假設λ,μ∈[0,1]且λ〈μ。

定義7[16]設Ω,X是非空給定集合，則稱映射A:X×Ω→[0,1]為X的Ω-模糊集。

3 N(2,2,0)代數的(∈δ,∈δ∨qδ(λ,μ))-模糊理想

4 N(2,2,0)代數的(∈δ,∈δ∨)-模糊子代數

5 結束語

給定一個集合Ω，提出了模糊點和模糊集間更為廣泛的“∈δ（Ω-屬于）”和“（Ω-重于）”關系的定義，并將其應用于N(2,2,0)代數，給出了(∈δ,∈δ∨)-模糊理想和(∈δ,∈δ∨)-模糊子代數的概念；研究了它們的一些基本性質及相互之間的關系，獲得了一些有學術意義的結論。在后續的工作中，將對(∈δ,∈δ∨)-模糊代數做進一步的研究。

[1]Wu Wangming.Fuzzy implication algebras[J].Fuzzy Systems and Mathematics,1990,4(1):56-64.

[2]Deng Fang'an,Xu Yang.OnN(2,2,0)algebras[J].Journal of Southwest Jiaotong University,1996,34(4):20-27.

[3]Deng Fang'an,Xu Yang,Yuan Jian.Ideal and relevanti deal ofN(2,2,0)algebras[J].Journal of Hanzhong Teachers College:Natural Science,1998,16(1):6-9.

[4]Chen Lu.Medial idempotents ofN(2,2,0)algebras[J].Pure andApplied Mathematics,2011,27(4):433-436.

[5]Li Xudong,Song Xuemei.A subalgebra ofN(2,2,0)algebras[J].Acta Scientiarum Naturalium Universitatis Nankaiensis:Natural Science,2012,45(3):57-61.

[6]Deng Fang'an,Yong Longquan.Regular semigroups ofN(2,2,0)algebras[J].Advances in Mathematics,2012,41 (6):665-671.

[7]Deng Fang'an.E-inversive semigroups ofN(2,2,0)algebra[J]. Journal of Mathematics,2014,34(5):977-984.

[8]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8 (3):338-353．

[9]Pu Paoming,Liu Yingming.Fuzzy topology(I)neighborhood structure of a fuzzy point and Moore-Smith convergence[J].Journal of Mathematical Analysis and Applications,1980,76(2):571-599．

[10]Pu Paoming,Liu Yingming.Fuzzy topology(II)product and quotient spaces[J].Journal of Mathematical Analysis and Applications,1980,77(1):20-37．

[11]Bhakat S K,Das P.On the definition of a fuzzy subgroup [J].Fuzzy Sets Systems,1992,51(2):235-241．

[12]Liao Zuhua,Yi Lihua,Hu Miaohan.(∈,∈∨q(λ,μ))-fuzzykideals of semigroups[J].Journal of Mathematics,2012,32 (2):191-205.

[13]Liao Zuhua,Hao Cuiyun,Chen Yunsheng.Generalized fuzzy completely semiprime(prime)ideals of a rings[J].Information an International Interdisciplinary Journal,2012, 15(6):2539-2542.

[14]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy positive implicative ideal ofN(2,2,0)algebra[J].Journal of Frontiers of Computer Science and Technology, 2014,8(5):622-629.

[15]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈∨q(λ,μ))-fuzzy associative ideal ofN(2,2,0)algebra[J].Computer Engineering andApplications,2014,50(12):54-58.

[16]Young B J,Kyung H K.OnΩ-fuzzy ideals of BCK/BCI-algebras[J].The Journal of Fuzzy Mathematics,2001,9(1): 173-180.

[17]Zhan Jianming,Tan Zhisong.Ω-fuzzy dot ideals of BCK/ BCI-algebras[J].Fuzzy Systems and Mathematics,2005,19 (2):54-57.

[18]Peng Jiayin.Ω-fuzzy P-ideals of BCI-algebras[J].Journal of Neijiang Normal University,2008,23(12):8-15.

[19]Peng Jiayin.Ω-fuzzy H-ideals of BCI-algebras[J].Journal of Neijiang Normal University,2009,24(2):5-10.

[20]Peng Jiayin.Ω-fuzzy dot ideals of BCH-algebras[J].Fuzzy Systems and Mathematics,2009,23(6):5-11.

[21]Peng Jiayin.Ω-fuzzy positive implicative ideals in BCK-algebras[J].Mathematics in Practice and Theory,2010,40 (2):157-163.

[22]Zhu Xiaoying,Liao Zuhua,Luo Xiaotang,et al.Ω-fuzzy subsemigroup of semigroups[J].Journal of Jiangnan University:Natural Science Edition,2013,12(3):343-346.

[23]Luo Xiaotang,Liao Zuhua,Zhu Xiaoying,et al.GeneralizedΩ-fuzzy bi-ideals of semigroups[J].Journal of Jiangnan University:Natural Science Edition,2013,12(4):480-484.

[24]Luo Xiaotang,Liao Zuhua,Zhu Xiaoying,et al.Ω-fuzzy interior ideals of semigroups[J].Journal of Jiangnan University:Natural Science Edition,2014,12(4):400-494.

[25]Zhu Chan,Liao Zuhua,Luo Xiaotang,et al.Ω-fuzzy complemented subsemiring[J].Fuzzy Systems and Mathematics, 2014,28(5):11-18.

[26]Liu Weifeng.Ω-fuzzy subalgebra of Boolean algebra[J]. Journal of Hubei University:Natural Science,2013,35(2): 144-148.

[27]Tang Huajing,Zhang Hui.Ω-fuzzy soft rings[J].Computer Engineering andApplications,2015,51(9):122-124.

附中文參考文獻：

[1]吳望名.Fuzzy蘊涵代數[J].模糊系統與數學,1990,4(1): 56-64．

[2]鄧方安,徐揚.關于N(2,2,0)代數[J].西南交通大學學報, 1996,34(4):20-27．

[3]鄧方安,徐揚,袁儉.N(2,2,0)代數的理想與關聯理想[J].漢中師范學院學報:自然科學版,1998,16(1):6-9.

[4]陳露.關于N(2,2,0)代數的中間冪等元[J].純粹數學與應用數學,2011,27(4):433-436．

[5]李旭東,宋雪梅.一個N(2,2,0)子代數[J].南開大學學報:自然科學版,2012,45(3):57-61．

[6]鄧方安,雍龍泉.N(2,2,0)代數的正則半群[J].數學進展, 2012,41(6):665-671．

[7]鄧方安.N(2,2,0)代數的E-反演半群[J].數學雜志,2014, 34(5):977-984.

[14]張建忠,傅小波,廖祖華.N(2,2,0)代數的(∈,∈∨q(λ,μ))-模糊正關聯理想[J].計算機科學與探索,2014,8(5):622-629.

[15]張建忠,傅小波,廖祖華.N(2,2,0)代數的(∈,∈∨q(λ,μ))-模糊結合理想[J].計算機工程與應用,2014,50(12):54-58.

[17]詹建明,譚志松.BCK/BCI-代數的Ω-模糊點理想[J].模糊系統與數學,2005,19(2):54-57.

[20]彭家寅.BCH-代數的Ω-模糊點理想[J].糊系統與數學, 2009,23(6):5-11.

[21]彭家寅.BCH-代數的Ω-模糊正定關聯理想[J].數學的實踐與認識,2010,40(2):157-163.

[22]朱曉英,廖祖華,羅曉棠,等.半群的Ω-模糊子半群[J].江南大學學報:自然科學版,2013,12(3):343-346.

[23]羅曉棠,廖祖華,朱曉英,等.半群的廣義Ω-模糊雙理想[J].江南大學學報:自然科學版,2013,12(4):480-484.

[24]羅曉棠,廖祖華,朱曉英,等.半群的Ω-模糊內理想[J].江南大學學報:自然科學版,2014,13(4):490-494.

[25]朱嬋,廖祖華,羅曉棠,等.Ω-模糊可補子半環[J].模糊系統與數學,2014,28(5):11-18.

[26]劉衛鋒.布爾代數的Ω-模糊子代數[J].湖北大學學報:自然科學版,2013,35(2):144-148.

[27]湯華晶,張慧.Ω-模糊軟環[J].計算機工程與應用,2015, 51(9):122-124.

FU Xiaobo was born in 1980.He is a lecturer at Wuxi Institute of Technology,and the member of CCF.His research interests include artificial intelligence and granular computing,etc.

傅小波（1980—），男，江蘇灌云人，無錫職業技術學院講師，CCF會員，主要研究領域為人工智能，粒計算等。

LIAO Zuhua was born in 1957.He is a professor and M.S.supervisor at Jiangnan University.His research interests include artificial intelligence and granular computing,etc.

廖祖華（1957—），男，江西奉新人，江南大學教授、碩士生導師，主要研究領域為人工智能，粒計算等。發表學術論文100多篇，主持省部級基金項目多項。

(∈δ,∈δ∨qδ(λ,μ))-Fuzzy Ideals ofN(2,2,0)Algebras*

FU Xiaobo1,LIAO Zuhua2+
1.Wuxi Institute of Technology,Wuxi,Jiangsu 214121,China
2.School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:liaozuhua57@aliyun.com

In this paper,“Ω-belongs to(∈δ)”and“Ω-quasi-coincident with()”relationships are generalized by the view of“belongs to(∈)”and“quasi-coincident with(q)”relationships between the fuzzy point and the fuzzy set.The definition of-fuzzy algebra is presented.Combining the-fuzzy algebras and theN(2,2,0)algebras,the concepts of pointwise-fuzzy ideals andΩ(λ,μ)-fuzzy ideals are introduced, and the equivalence relationship of this two definitions is discussed.Some basic properties of them are also studied.Finally,this paper proposes the concepts of pointwise-fuzzy subalgebras andΩ(λ,μ)-fuzzy subalgebras, and studies the mutual relationships between-fuzzy ideals and-fuzzy subalgebras.

N(2,2,0)algebra;-fuzzy ideals;-fuzzy subalgebras

10.3778/j.issn.1673-9418.1512084

A

TP18

*The National Natural Science Foundation of China under Grant Nos.611702121,11401259(國家自然科學基金);the Natural Science Foundation of Jiangsu Province under Grant No.BK2015117(江蘇省自然科學基金);the Scientific Research Subject of Wuxi Institute of Technology under Grant No.3116015931(無錫職業技術學院科研課題).

Received 2015-12,Accepted 2016-03.

CNKI網絡優先出版:2016-03-17,http://www.cnki.net/kcms/detail/11.5602.TP.20160317.1129.002.html

FU Xiaobo,LIAO Zuhua.(∈δ,∈δ∨qδ(λ,μ))-fuzzy ideals ofN(2,2,0)algebras.Journal of Frontiers of Computer Science and Technology,2017,11(2)：323-332.