基于簡(jiǎn)便約束粒子群優(yōu)化算法的空空導(dǎo)彈μ-PID控制器設(shè)計(jì)

張民，陳亮，陳欣

(南京航空航天大學(xué) 自動(dòng)化學(xué)院, 江蘇 南京 211106)

基于簡(jiǎn)便約束粒子群優(yōu)化算法的空空導(dǎo)彈μ-PID控制器設(shè)計(jì)

張民，陳亮，陳欣

(南京航空航天大學(xué) 自動(dòng)化學(xué)院, 江蘇 南京 211106)

針對(duì)現(xiàn)有約束粒子群優(yōu)化(PSO)算法存在的算法復(fù)雜、應(yīng)用范圍受限、優(yōu)化效果不佳等缺陷，提出一種新型約束粒子群算法。該算法采用目標(biāo)函數(shù)替換的方法將約束優(yōu)化問(wèn)題轉(zhuǎn)化為非約束優(yōu)化問(wèn)題，具有簡(jiǎn)便易用的優(yōu)點(diǎn)。通過(guò)典型測(cè)試函數(shù)測(cè)試并和其他具有代表性的約束PSO算法進(jìn)行對(duì)比，表明該算法在處理約束優(yōu)化問(wèn)題上的優(yōu)越性。為了驗(yàn)證該算法應(yīng)用于工程的可行性，以樣例導(dǎo)彈縱向模型為對(duì)象，針對(duì)經(jīng)典Raytheon控制結(jié)構(gòu)，采用該算法設(shè)計(jì)了μ-PID控制器。仿真結(jié)果表明，樣例導(dǎo)彈控制器可以在滿足多種時(shí)域指標(biāo)的同時(shí)具有良好的魯棒性能，達(dá)到了設(shè)計(jì)指標(biāo)要求，驗(yàn)證了所提出算法的有效性。

飛行器控制、導(dǎo)航技術(shù)；空空導(dǎo)彈；粒子群優(yōu)化；約束優(yōu)化；魯棒性

0 引言

近年來(lái)，采用非線性優(yōu)化算法來(lái)解決控制器優(yōu)化設(shè)計(jì)問(wèn)題的研究已逐步進(jìn)入應(yīng)用階段[1-2]。Kennedy等[3]在1995年提出的粒子群優(yōu)化(PSO)算法，作為其中有代表性的一種群體智能優(yōu)化算法，其具有如下優(yōu)點(diǎn)：1) 算法結(jié)構(gòu)簡(jiǎn)單，只需要很少的代碼就可以實(shí)現(xiàn)該算法；2) 算法程序在計(jì)算量和內(nèi)存占用方面很小，有利于在計(jì)算機(jī)上實(shí)現(xiàn)復(fù)雜系統(tǒng)的優(yōu)化；3) 與某些優(yōu)化算法不同，PSO算法對(duì)目標(biāo)函數(shù)沒(méi)有諸如線性、可微、凸集等要求；4) 算法對(duì)粒子的初值不敏感。目前，PSO算法已被廣泛應(yīng)用于多目標(biāo)優(yōu)化、神經(jīng)網(wǎng)絡(luò)系統(tǒng)訓(xùn)練、模糊系統(tǒng)控制和決策支持等各領(lǐng)域[1-2, 4]。

標(biāo)準(zhǔn)的PSO算法無(wú)法處理帶等式或不等式約束條件的優(yōu)化問(wèn)題，這限制了PSO算法在實(shí)際工程中的應(yīng)用。為了處理約束優(yōu)化問(wèn)題，大量的改進(jìn)算法相繼被提出[2, 4]，Michalewicz等[5]在1996年共同提出了罰函數(shù)PSO算法，Bouallègue等[6]在2011年將其應(yīng)用于定結(jié)構(gòu)H∞控制器的設(shè)計(jì)中。為了解決傳統(tǒng)的罰函數(shù)PSO算法難以選取合適的懲罰因子的缺陷，蔡海鸞等[7]在2015年提出了一種新的自適應(yīng)懲罰函數(shù)法，該方法通過(guò)依據(jù)每一步迭代過(guò)程中違背約束條件粒子所占比例來(lái)動(dòng)態(tài)調(diào)整懲罰因子，從而解決了懲罰因子選擇困難問(wèn)題，成為現(xiàn)今廣泛被采用的一種新型懲罰函數(shù)法。該算法的不足之處在于其收斂性能對(duì)于需調(diào)參數(shù)α有很強(qiáng)的依賴(lài)性，而該參數(shù)的選擇需要依據(jù)工程人員豐富的經(jīng)驗(yàn)。Sedlaczek等[8]在2006年提出了增廣拉格朗日PSO(ALPSO)算法來(lái)處理約束優(yōu)化問(wèn)題，Kim等[9]在2008年將其應(yīng)用于PID控制器的設(shè)計(jì)中。ALPSO算法的不足之處在于為了處理約束條件而引入了拉格朗日算子，這增加了算法的復(fù)雜性，并且該方法還對(duì)目標(biāo)函數(shù)有連續(xù)、可微的要求，限制了該方法的應(yīng)用范圍。上述算法是PSO算法在處理約束優(yōu)化問(wèn)題中目前具有代表性的方法。

本文提出了一種采用PSO算法處理約束優(yōu)化問(wèn)題的新穎且簡(jiǎn)便易用的算法，該方法的主要優(yōu)點(diǎn)是在處理約束條件時(shí)沒(méi)有引入任何新的需調(diào)參數(shù)，并且具有優(yōu)良的搜索性能，對(duì)目標(biāo)函數(shù)也沒(méi)有連續(xù)可微等要求。利用典型測(cè)試函數(shù)[10]對(duì)該簡(jiǎn)便約束PSO算法在處理約束優(yōu)化問(wèn)題上的性能進(jìn)行了綜合測(cè)試，并和其他算法進(jìn)行比較。同時(shí)，針對(duì)傳統(tǒng)魯棒控制方法如H∞方法、μ綜合方法設(shè)計(jì)的導(dǎo)彈控制器存在的階次過(guò)高、難以實(shí)現(xiàn)等問(wèn)題[11]，將所提出的簡(jiǎn)便約束PSO算法應(yīng)用到導(dǎo)彈控制律的優(yōu)化設(shè)計(jì)中，設(shè)計(jì)了一種能夠滿足現(xiàn)代空戰(zhàn)對(duì)于導(dǎo)彈魯棒性能要求的μ-PID定結(jié)構(gòu)控制器。仿真結(jié)果表明所設(shè)計(jì)的控制器在滿足多種時(shí)域指標(biāo)的同時(shí)具有良好的穩(wěn)定魯棒性和性能魯棒性，從而驗(yàn)證了簡(jiǎn)便約束PSO算法應(yīng)用于工程實(shí)際的可行性。

1 PSO算法

PSO算法是由美國(guó)社會(huì)心理學(xué)家Kennedy等[3]在1995年共同提出的一種進(jìn)化計(jì)算技術(shù)，它是一種通過(guò)模擬鳥(niǎo)類(lèi)群體行為進(jìn)行建模與仿真研究而發(fā)展起來(lái)的一種基于群體協(xié)作的隨機(jī)搜索算法，屬于群體智能搜索算法的一種，也稱(chēng)為微粒群算法。該算法原理是從一組隨機(jī)的初始值出發(fā)，采用基于鄰域的搜索技術(shù)，通過(guò)迭代來(lái)尋找最優(yōu)解，在每一次迭代中，粒子通過(guò)個(gè)體極值(粒子本身找到的最優(yōu)解)和群體極值(種群目前找到的最優(yōu)解)來(lái)更新自己。由于PSO算法本身結(jié)構(gòu)簡(jiǎn)單，并在多種復(fù)雜非凸優(yōu)化問(wèn)題的應(yīng)用中表現(xiàn)優(yōu)異，近年來(lái)引起了越來(lái)越多的關(guān)注。

1.1 標(biāo)準(zhǔn)PSO算法

在PSO算法中，每一個(gè)優(yōu)化問(wèn)題的解作為一只單個(gè)的鳥(niǎo)，或稱(chēng)為粒子，粒子的屬性包括其位置x和速度v. 每個(gè)粒子在多維空間中依據(jù)個(gè)體經(jīng)驗(yàn)和群體中其他粒子的經(jīng)驗(yàn)來(lái)動(dòng)態(tài)調(diào)整自身移動(dòng)的軌跡與速度。在第k次迭代中，第i個(gè)粒子xi=(xi,1,xi,2,…,xi,m)∈Rm依據(jù)以下公式對(duì)位置和速度進(jìn)行調(diào)整：

(1)

(2)

(3)

(5)

cw,max和cw,min分別為cw的最大值與最小值，kmax為最大進(jìn)化代數(shù)。

1.2 約束PSO算法

PSO算法最初是作為一種非約束優(yōu)化算法被提出的，然而在大量的工程實(shí)踐中，有相當(dāng)多的應(yīng)用屬于要求滿足一定不等式約束條件下的優(yōu)化問(wèn)題。典型的約束PSO算法有自適應(yīng)懲罰函數(shù)PSO算法和ALPSO算法，然而這兩種算法均有一些如前所述不足之處。為了克服這些不足，本文提出了一種新型簡(jiǎn)便易用的約束PSO算法。

一般約束優(yōu)化問(wèn)題可以描述為

(6)

式中：函數(shù)h(x)=[h1(x),h2(x),…,hn(x)]，(Rm→Rn)表示約束條件；F表示所有可行的區(qū)域，在本文中，假設(shè)F為非空集合。

本文采用如下一種新穎簡(jiǎn)便的方法將(6)式所描述的約束優(yōu)化問(wèn)題轉(zhuǎn)化為(7)式所示的非約束優(yōu)化問(wèn)題，在該過(guò)程中不需要增加任何新的算法參數(shù)。

(7)

式中：fm(x)定義為

(8)

本文提出的算法最大的優(yōu)勢(shì)在于其簡(jiǎn)便性，它不需要像ALPSO算法那樣要求目標(biāo)函數(shù)連續(xù)可微，也不需要像自適應(yīng)罰函數(shù)法那樣增加新的需調(diào)參數(shù)。在后續(xù)內(nèi)容中，該算法將與ALPSO算法、罰函數(shù)法進(jìn)行性能比較。

2 算法性能測(cè)試

目前，非線性優(yōu)化算法的優(yōu)劣尚不能從理論上進(jìn)行證明，通常只能通過(guò)測(cè)試函數(shù)的實(shí)測(cè)結(jié)果來(lái)進(jìn)行比較。為了驗(yàn)證所提出的約束PSO算法的性能，在本部分內(nèi)容中采用了多個(gè)標(biāo)準(zhǔn)測(cè)試函數(shù)[10]來(lái)對(duì)其性能進(jìn)行全面測(cè)試與驗(yàn)證。在文獻(xiàn)[10]中包含24個(gè)標(biāo)準(zhǔn)測(cè)試函數(shù)，我們選擇了其中帶不等式約束的單目標(biāo)優(yōu)化問(wèn)題共12個(gè)測(cè)試函數(shù)，這些測(cè)試函數(shù)在約束優(yōu)化算法的性能測(cè)試中被廣泛采用。

測(cè)試程序在Matlab 7.8環(huán)境下運(yùn)行，采用一臺(tái)Intel i5 CPU PC機(jī)，內(nèi)存為4 GB. 每個(gè)任務(wù)運(yùn)行30次，算法停止的條件是達(dá)到最大進(jìn)化代數(shù)1 000. 同時(shí)為了與前述自適應(yīng)罰函數(shù)法PSO算法、ALPSO算法進(jìn)行對(duì)比，對(duì)這兩種算法也進(jìn)行了同樣的測(cè)試。在進(jìn)行比較分析時(shí)，粒子群算法參數(shù)取為：粒子數(shù)量 30；粒子維數(shù)依測(cè)試函數(shù)；粒子最大移動(dòng)速度vmax,d=xmax,d/2；學(xué)習(xí)因子:cp=2,cs=2；慣性系數(shù)最大與最小值：wmax=0.9,wmin=0.4；最大搜索代數(shù): 1 000.

測(cè)試結(jié)果如表1所示。本文提出的簡(jiǎn)便約束PSO算法在處理帶約束的優(yōu)化問(wèn)題中具有優(yōu)越的性能，對(duì)測(cè)試函數(shù)尋優(yōu)的成功率明顯高于自適應(yīng)罰函數(shù)PSO算法和ALPSO算法，并且得到的最終優(yōu)化結(jié)果及其分布特性也優(yōu)于上述兩種算法。

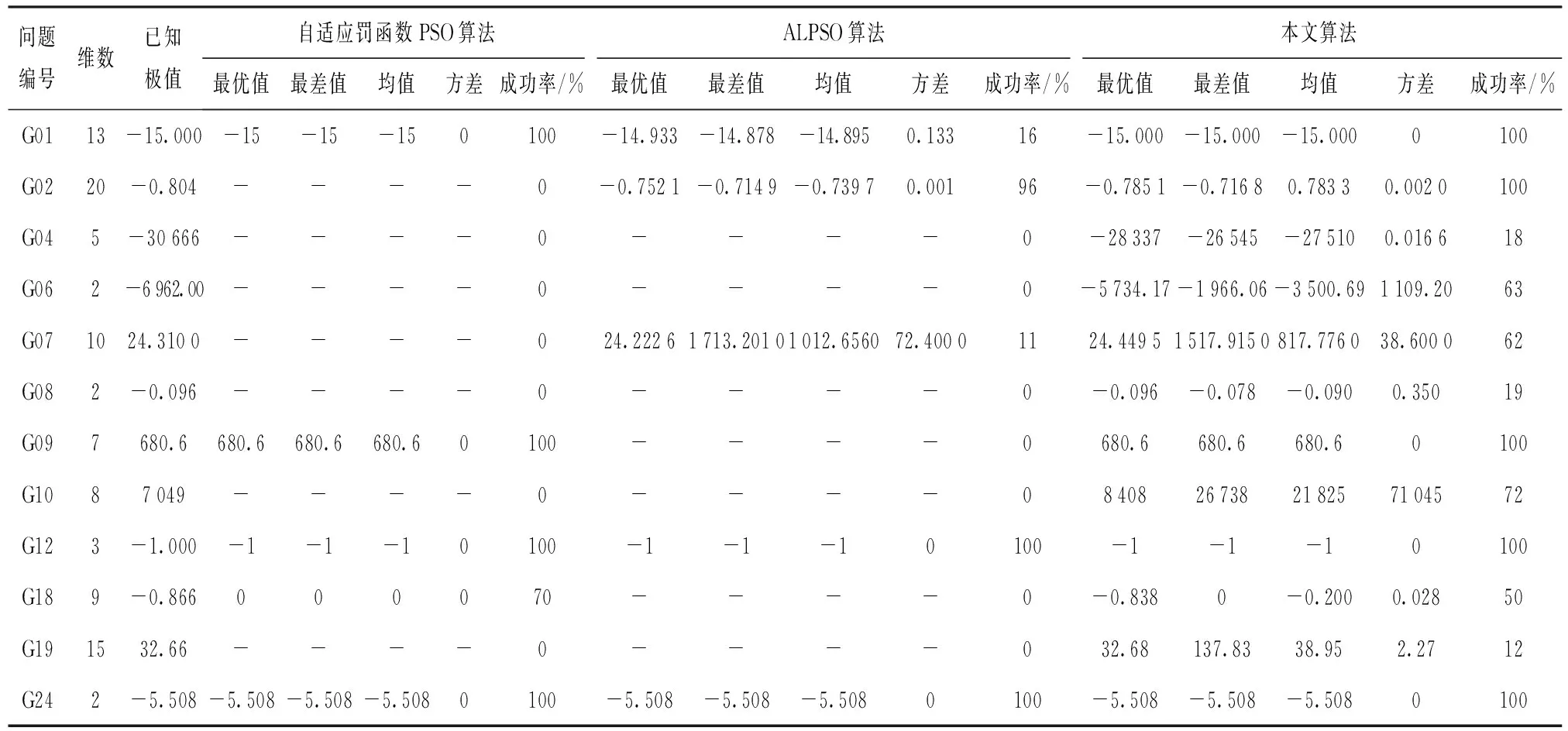
表1 3種約束優(yōu)化算法測(cè)試結(jié)果Tab.1 Test results of three constrained optimization algorithms

3 導(dǎo)彈μ-PID控制應(yīng)用

3.1 問(wèn)題描述

3.1.1μ分析方法

結(jié)構(gòu)奇異值μ是一種線性代數(shù)工具，用來(lái)定量的表征結(jié)構(gòu)化不確定性對(duì)線性動(dòng)態(tài)系統(tǒng)穩(wěn)定性及性能的影響。相比于H∞方法，μ綜合方法可以同時(shí)分析控制系統(tǒng)的魯棒穩(wěn)定性和魯棒性能[11-14]。

對(duì)任意多輸入不確定線性閉環(huán)系統(tǒng)，總可以由圖1所示的結(jié)構(gòu)來(lái)描述。其中M代表系統(tǒng)傳遞函數(shù)矩陣，由控制器和控制對(duì)象構(gòu)成。

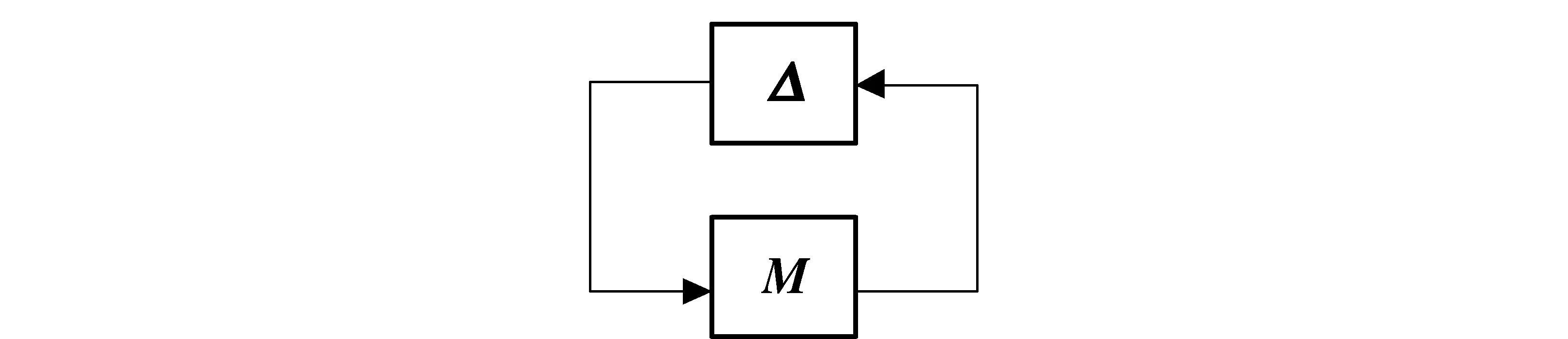
圖1 標(biāo)準(zhǔn)反饋控制結(jié)構(gòu)Fig.1 Standard feedback control structure

Δ代表模型不確定性，即作為控制對(duì)象的數(shù)學(xué)模型與實(shí)際對(duì)象存在的差異，且有

(9)

(10)

若系統(tǒng)不確定性Δ滿足(10)式，則系統(tǒng)傳遞函數(shù)矩陣M的結(jié)構(gòu)奇異值定義為

(11)

直接按照(11)式來(lái)求解結(jié)構(gòu)奇異值μ是非常困難的，通常采用的是一種逼近方法。首先計(jì)算μ值的上下界，當(dāng)上下界之差足夠小時(shí)，取其為近似值，該方法稱(chēng)為“D-K”迭代法，由Doyle等[15]在1985年提出。

3.1.2μ-PID控制器設(shè)計(jì)問(wèn)題

μ分析問(wèn)題可由圖2表示。

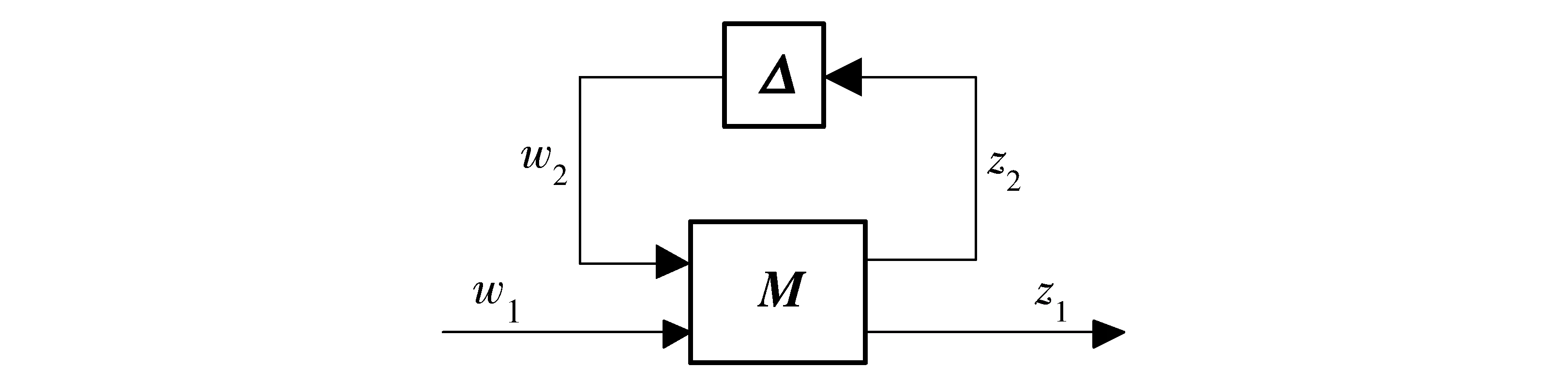
圖2 μ分析問(wèn)題結(jié)構(gòu)方塊圖Fig.2 Block diagram of μ analysis

在此結(jié)構(gòu)中，M代表廣義控制對(duì)象以及控制器，w1表示外部輸入信號(hào)，z2和w2分別表示模型不確定性的輸入和輸出信號(hào)，z1表示控制輸出信號(hào)。此時(shí)系統(tǒng)∑(s,x)可分解為

(12)

在本文中，基于約束優(yōu)化的μ-PID控制器設(shè)計(jì)可以描述為

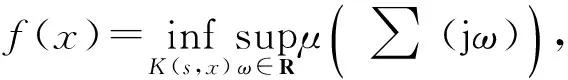
(13)

式中：K(s,x)表示控制器，x∈Rm為控制器參數(shù)。搜索其最小值并滿足由時(shí)域響應(yīng)指標(biāo)組成的約束條件。

3.2 導(dǎo)彈控制設(shè)計(jì)與仿真

樣例導(dǎo)彈采用基于多工作點(diǎn)線性化模型的控制律設(shè)計(jì)，6自由度非線性模型驗(yàn)證的方法，因此本文中控制律設(shè)計(jì)仍以線性化模型為設(shè)計(jì)對(duì)象。以樣例導(dǎo)彈在15 000 m高度、馬赫數(shù)為2.8、40°攻角下的特征工作點(diǎn)縱向通道狀態(tài)空間模型為例，其狀態(tài)方程為

輸出方程為

式中：u、w分別為縱向和法向速度；α為攻角；q為俯仰角速率；az為法向加速度；δe為等效升降舵偏角。

導(dǎo)彈的定結(jié)構(gòu)控制器可以有各種形式，如姿態(tài)控制器、迎角控制器和過(guò)載控制器等，每種控制器依據(jù)控制對(duì)象本身的特性和控制需求還可以細(xì)分為更多的回路控制結(jié)構(gòu)。不失一般性，本文以經(jīng)典Raytheon駕駛儀控制結(jié)構(gòu)為例，其縱向控制結(jié)構(gòu)如圖3所示。

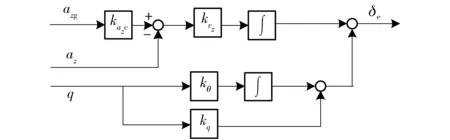
圖3 樣例導(dǎo)彈縱向Raytheon駕駛儀控制結(jié)構(gòu)Fig.3 Sample missile longitudinal Raytheon control structure

圖3中各項(xiàng)參數(shù)分別為：kazc為法向加速度指令增益系數(shù)；kvz為法向速度增益系數(shù)；kθ為俯仰角增益系數(shù)；kq為俯仰角速率增益系數(shù)；Azg為給定法向加速度。

樣例導(dǎo)彈縱向通道所需滿足的時(shí)域性能指標(biāo)如表2所示。

表2 縱向通道階躍響應(yīng)性能指標(biāo)Tab.2 Longitudinal channel step response performance index

采用如上所述性能指標(biāo)函數(shù)和約束條件，基于3種不同PSO算法的優(yōu)化結(jié)果如表3～表5所示。表3～表5中的Pm、Gm分別為相角裕度和幅值裕度。

本文方法的最終設(shè)計(jì)結(jié)果體現(xiàn)在表5中，并且由表3～表5可知，罰函數(shù)PSO算法所得到的3種μ值均最大，μ最小值大于1，表明該優(yōu)化方法所得到的控制器魯棒性較差；ALPSO算法總體性能次之；本文提出的簡(jiǎn)便約束PSO算法顯然具有最佳的性能，并且傳統(tǒng)的幅值和相角裕度指標(biāo)也驗(yàn)證了這一結(jié)果。基于上述3種PSO算法的目標(biāo)函數(shù)收斂性曲線如圖4～圖6所示。

表3 罰函數(shù)PSO算法優(yōu)化結(jié)果Tab.3 Statistical analysis of optimized results: PSO with adaptive penalty functions-design case

表4 ALPSO算法優(yōu)化結(jié)果Tab.4 Statistical analysis of optimizated results: ALPSO-design case

表5 本文算法優(yōu)化結(jié)果Tab.5 Statistical analysis of optimizated results: the proposed PSO-design case

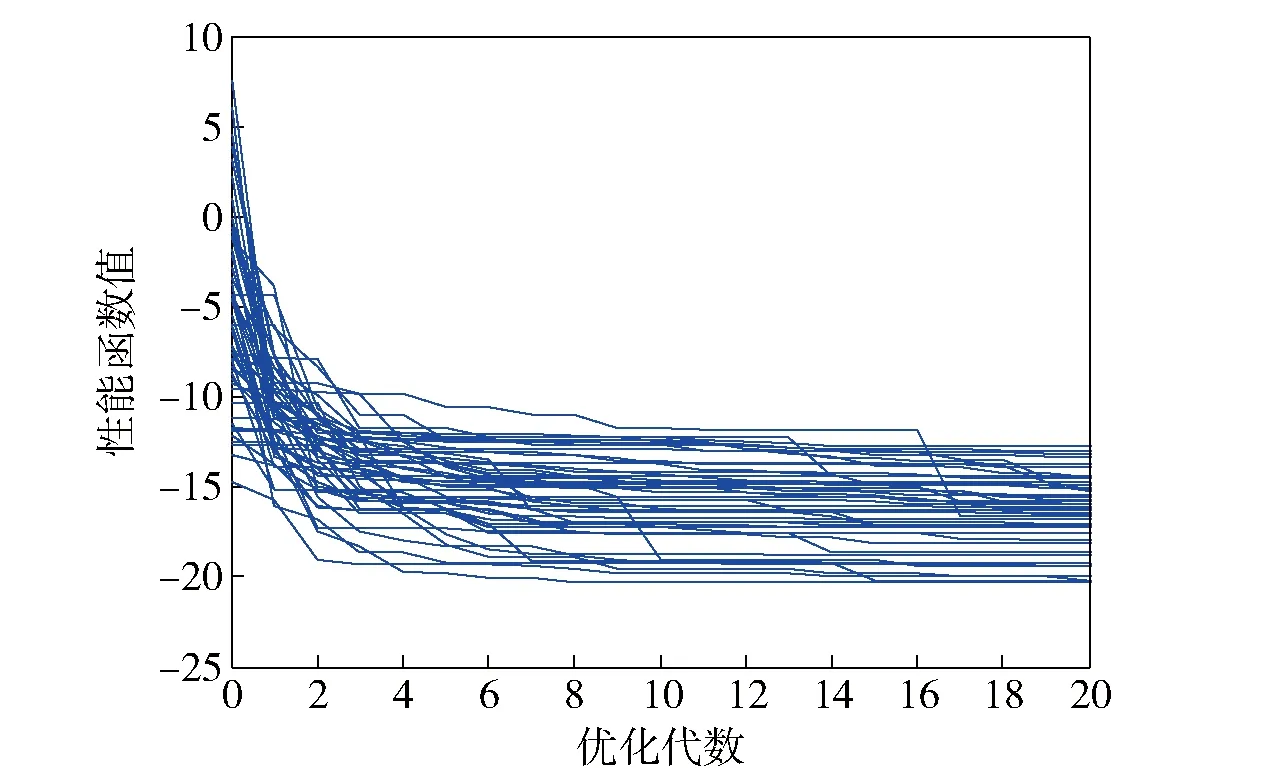
圖4 罰函數(shù)PSO算法目標(biāo)函數(shù)收斂性曲線Fig.4 Objective function convergence curves-PSO with adaptive penalty function

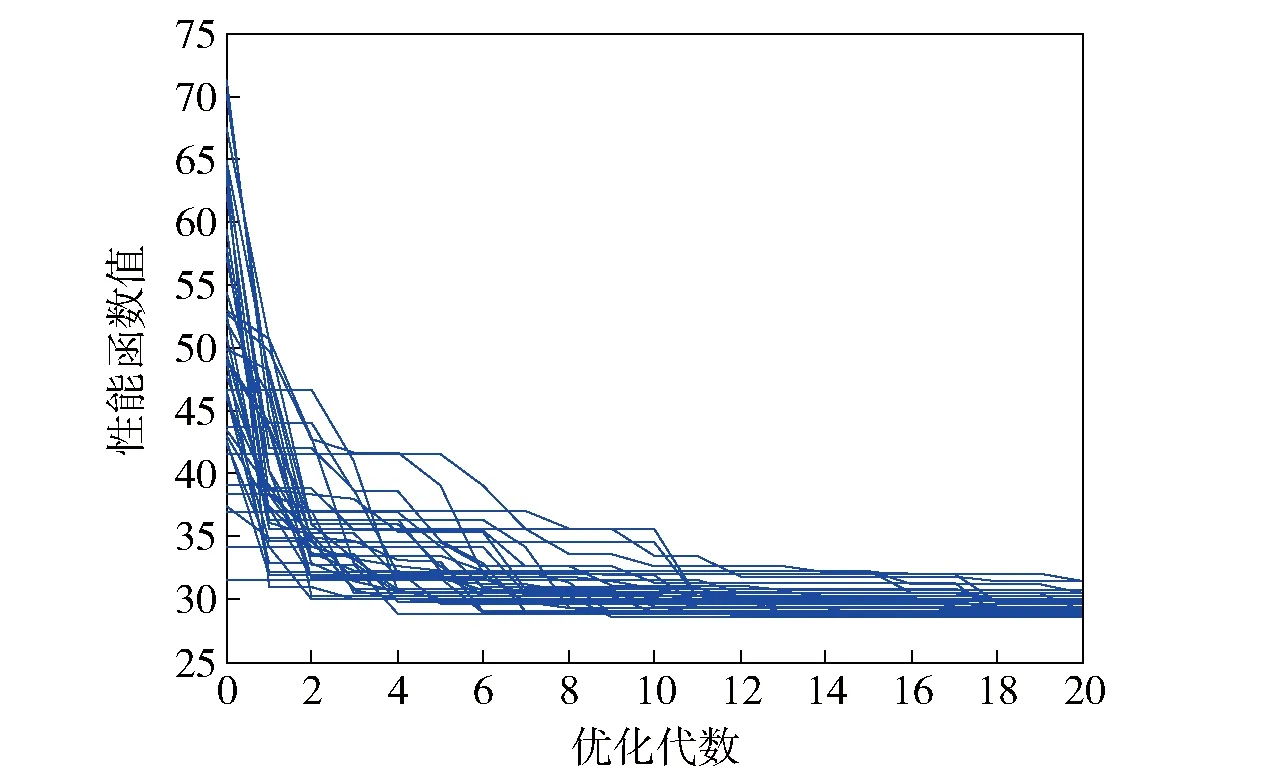
圖5 ALPSO算法目標(biāo)函數(shù)收斂性曲線Fig.5 Objective function convergence curves-ALPSO

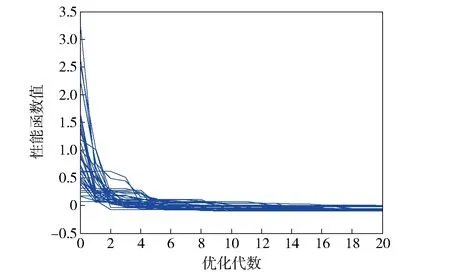
圖6 本文算法目標(biāo)函數(shù)收斂性曲線Fig.6 Objective function convergence curves-PSO presented in the present paper

由圖4～圖6明顯可見(jiàn)，相比于罰函數(shù)PSO算法和ALPSO算法，本文提出的簡(jiǎn)便約束PSO算法在設(shè)計(jì)樣例導(dǎo)彈縱向通道控制律過(guò)程中具有最好的統(tǒng)計(jì)收斂特性。

在簡(jiǎn)便約束PSO算法得到的50次結(jié)果中，選取最優(yōu)值結(jié)果:kazc=0.97，kvz=0.2，kθ=2.44,kq=0.41作為控制參數(shù)，并且在圖7所示的俯仰通道閉環(huán)系統(tǒng)中，wi為理想相應(yīng)權(quán)函數(shù)，wp為模型性能指標(biāo)權(quán)函數(shù)，win為模型不確定性權(quán)函數(shù)，wn為噪聲干擾權(quán)函數(shù)，Δin為模型不確定性,du為模型不確定性輸入的干擾信號(hào)，dn為噪聲輸入的干擾信號(hào)，zazo為az的輸出信號(hào)測(cè)量值。權(quán)函數(shù)取值參見(jiàn)參考文獻(xiàn)[16]。

對(duì)閉環(huán)控制系統(tǒng)的頻域和時(shí)域性能分析如下：

1)頻域性能分析。

①魯棒穩(wěn)定性分析。在圖7所示的俯仰通道閉環(huán)系統(tǒng)中，令外輸入為0，僅考慮輸入端乘型不確定性Δin作用下zazo的響應(yīng)。如圖8(a)所示為從du到zazo的傳遞函數(shù)的結(jié)構(gòu)奇異值上界曲線。由圖8(a)中可見(jiàn)結(jié)構(gòu)奇異值均在0.3以下，表明系統(tǒng)具有良好的魯棒穩(wěn)定性。

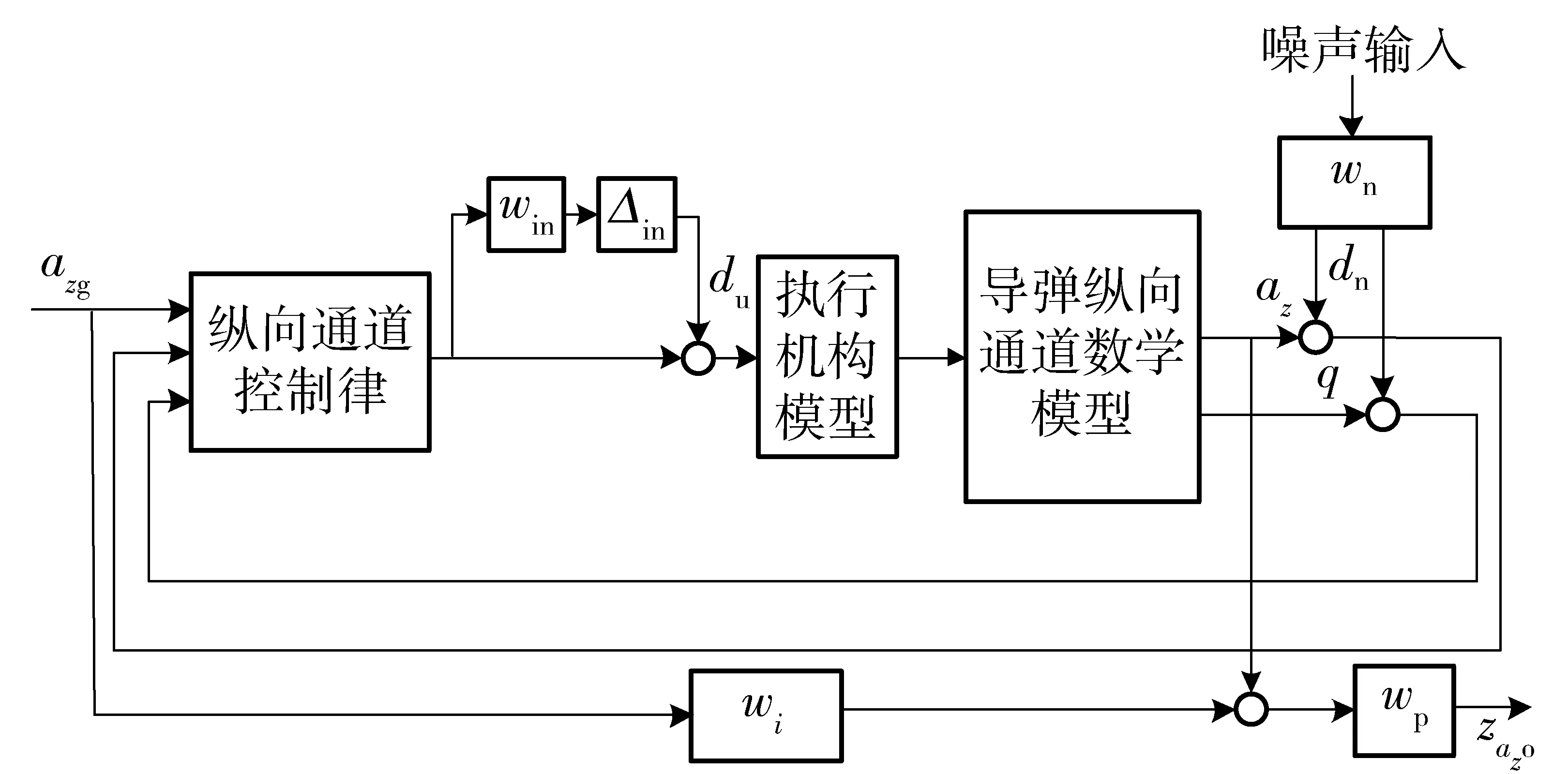
圖7 閉環(huán)系統(tǒng)魯棒性驗(yàn)證仿真結(jié)構(gòu)Fig.7 Closed-loop system robustness verification simulation structure

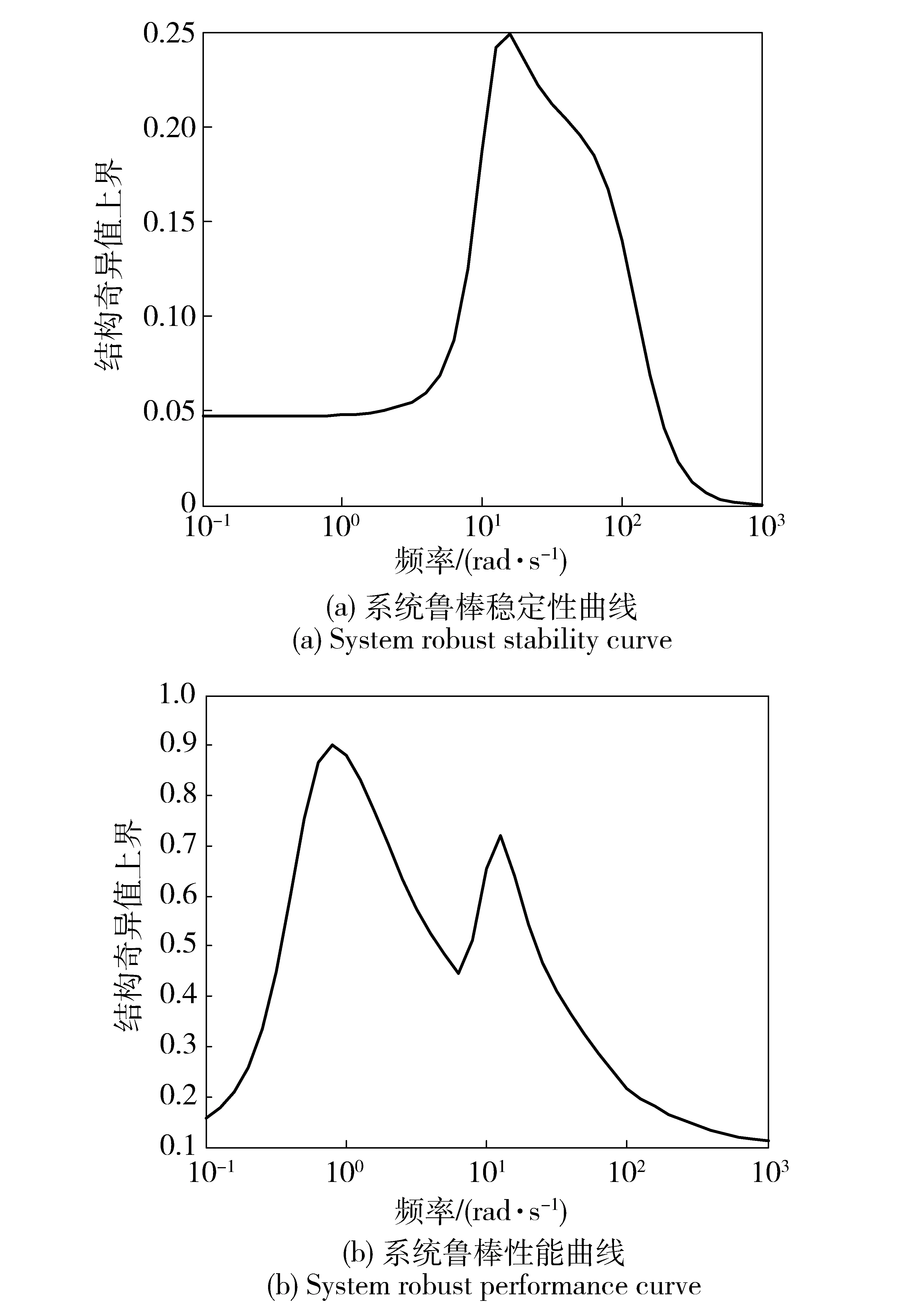
圖8 系統(tǒng)魯棒曲線Fig.8 System robust curve

②魯棒性能分析。考察在外輸入和輸入端乘型不確定性同時(shí)作用下系統(tǒng)的性能。如圖8(b)所示，結(jié)構(gòu)奇異值均在1以下，表明系統(tǒng)的魯棒性能也滿足指標(biāo)要求。

2)時(shí)域性能分析。

①標(biāo)稱(chēng)系統(tǒng)單位階躍響應(yīng)。在圖7所示的俯仰通道閉環(huán)系統(tǒng)中，令Δin=0且擾動(dòng)dn=0,僅考慮俯仰通道過(guò)載命令azg=1作用下系統(tǒng)的階躍響應(yīng)。從圖9可見(jiàn)，系統(tǒng)的標(biāo)稱(chēng)性能滿足表2所示的時(shí)域性能指標(biāo)。

②攝動(dòng)系統(tǒng)單位階躍響應(yīng)。在外輸入和輸入端乘型不確定性同時(shí)作用下系統(tǒng)的階躍響應(yīng)如圖10所示，可知系統(tǒng)在攝動(dòng)下的性能仍然滿足表2所示的時(shí)域性能指標(biāo)，從而印證了頻域分析的結(jié)果。

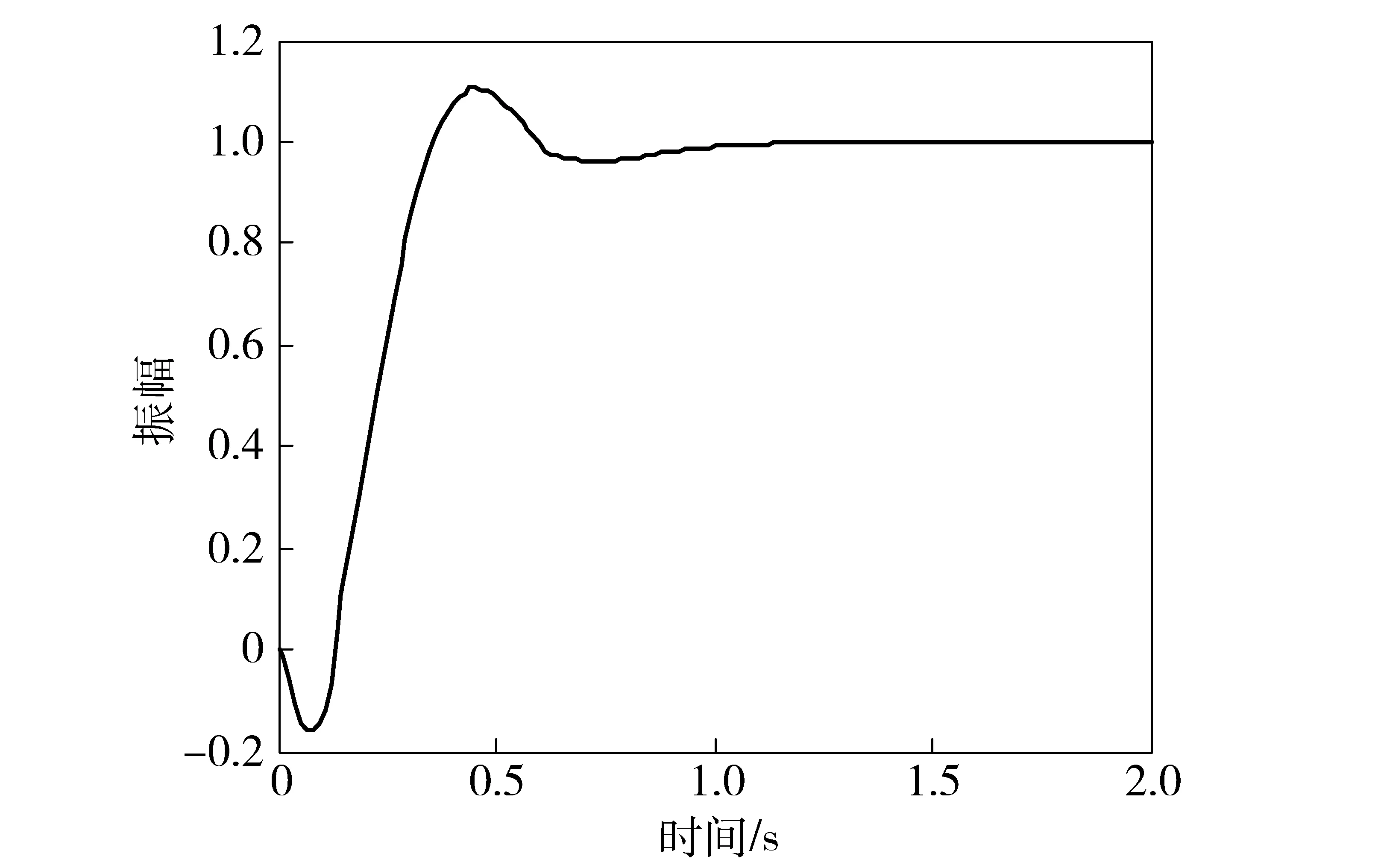
圖9 標(biāo)稱(chēng)系統(tǒng)階躍響應(yīng)曲線Fig.9 Nominal performance response curve

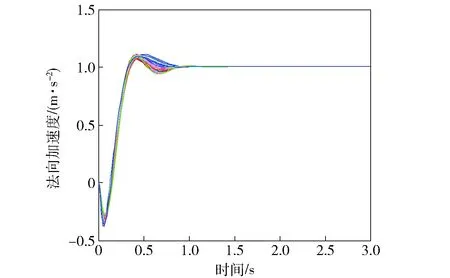
圖10 攝動(dòng)系統(tǒng)階躍響應(yīng)曲線Fig.10 Perturbation system performance curves

4 結(jié)論

1)本文提出了一種新穎且簡(jiǎn)便易用的約束PSO算法，并將其應(yīng)用到導(dǎo)彈駕駛儀定結(jié)構(gòu)魯棒控制器的設(shè)計(jì)中。通過(guò)典型測(cè)試函數(shù)的測(cè)試，并與其他約束優(yōu)化PSO算法進(jìn)行對(duì)比，表明了本文提出的算法在解決約束優(yōu)化問(wèn)題中的優(yōu)越性。

2)以某樣例導(dǎo)彈縱向通道數(shù)學(xué)模型為控制對(duì)象，采用該簡(jiǎn)便約束PSO算法設(shè)計(jì)了μ-PID控制器，并對(duì)其時(shí)域性能和魯棒性進(jìn)行了分析，結(jié)果各項(xiàng)性能指標(biāo)滿足要求，從而驗(yàn)證了該算法的有效性。在本文中，僅對(duì)樣例導(dǎo)彈縱向通道控制器進(jìn)行了設(shè)計(jì)，在建立了μ-PID魯棒控制器設(shè)計(jì)方法的基礎(chǔ)上，將其推廣到導(dǎo)彈的三通道的聯(lián)合設(shè)計(jì)是下一步值得研究的工作。

References)

[1] 楊希祥, 降振宇, 張為華. 基于粒子群優(yōu)化的固體運(yùn)載火箭上升段彈道優(yōu)化設(shè)計(jì)研究[J]. 宇航學(xué)報(bào), 2010, 31(5): 1304-1309. YANG Xi-xiang, JIANG Zhen-yu, ZHANG Wei-hua. Solid rocket based on particle swarm optimization on the ballistic optimization design research [J]. Journal of Aerospace, 2010, 31(5):1304-1309.(in Chinese)

[2] 傅陽(yáng)光, 周成平, 丁明躍. 基于混合量子粒子群優(yōu)化算法的三維航跡規(guī)劃[J]. 宇航學(xué)報(bào), 2010, 31(12): 2657-2664. FU Yang-guang, ZHOU Cheng-ping, DING Ming-yue. Quantum particle swarm optimization algorithm based on hybrid 3D path planning [J]. Journal of Aerospace, 2010, 31(12):2657-2664. (in Chinese)

[3] Kennedy J, Eberhart R. Particle swarm optimization[C]∥IEEE International Joint Conference on Neural Networks. Perth, Austra-lia:IEEE, 1995:1942-1948.

[4] Afshar M H. Large scale reservoir operation by constrained particle swarm optimization algorithms [J]. Journal of Hydro-environment Research, 2012, 6(1):75-87.

[5] Michalewicz Z, Dasgupta D, Riche R, et al. Evolutionary algorithms for constrained engineering problems[J]. Computers & Industrial Engineering, 1996, 30(4):851-870.

[6] Bouallègue S, Haggège J, Benrejeb M. Particle swarm optimization-based fixed-structureH∞control design[J]. International Journal of Control, Automation, and Systems,2011, 9(2):258-266.

[7] Cai H L. A new adaptive penalty function in the application of genetic algorithm[J]. Journal of East China Normal University:Natural Science, 2015, 6(6):36-52.

[8] Sedlaczek K, Eberhard P. Using augmented Lagrangian particle swarm optimization for constrained problems in engineering[J]. Structural and Multidisciplinary Optimization, 2006, 32(4):277-286.

[9] Kim T H, Maruta I, Sugie T. Robust PID controller tuning based on the constrained particle swarm optimization[J]. Automatica, 2008, 44(4):1104-1110.

[10] Liang J J, Runarsson T P, Mezura-Montes E, et al. Problem de-finitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization[EB/OL]. [2006-09-18]. http:∥www.lania.mx/～emezura/util/files/tr_cec06.pdf.

[11] 鄭建華, 楊滌. 魯棒控制理論在傾斜轉(zhuǎn)彎導(dǎo)彈中的應(yīng)用[M]. 北京:國(guó)防工業(yè)出版社, 2001. ZHENG Jian-hua, YANG Di. Robust control theory in the application of bank missile[M]. Beijing: National Defense Industry Press, 2001. (in Chinese)

[12] Doyle J C. A review ofμfor case studies in robust control[C]∥10th IFAC Triennial World Congress. Munich, FRG:Pergamon Press, 1988:365-370.

[13] Li T J, Ma Y J. Robust vibration control flexble tensegrity structure viaμsynthesis[J]. Structure Control and Health Monitoring, 2013, 20(2):173-186.

[14] 李偉杰，沈作軍. 基于μ分析的高超聲速飛行器再入軌跡評(píng)估[J]. 飛行力學(xué), 2016, 34(4):50-53, 58. LI Wei-jie, SHEN Zuo-jun. An evaluation of hypersonic vehicle reentry trajectory based onμ-analysis[J]. Flight Dynamics, 2016, 34(4):50-53, 58.(in Chinese)

[15] Doyle J C, John C, Chu C C. Matrix interpolation andH∞performance bounds[C]∥American Control Conference. Boston, MA:IEEE,1985:129-134.

[16] 臧月進(jìn). 空- 空導(dǎo)彈μ綜合控制器設(shè)計(jì)與研究[D]. 南京:南京航空航天大學(xué), 2012. ZANG Yue-jin. The design and research ofμ-Air-to-air Missile integrated controller[J]. Nanjing:Nanijng University of Aeronautics and Astronautics, 2012.(in Chinese)

A Simple Constrained PSO Algorithm and Its Application inμ-PID Controller Design for Missile Autopilot

ZHANG Min, CHEN Liang, CHEN Xin

(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, Jiangsu, China)

The existing constrained particle swarm optimization(PSO) algorithms have the disadvantages of algorithm complexity, limited application and poor optimization. A kind of novel constrained particle swarm optimization algorithm is proposed. The proposed algorithm converts a constrained optimization problem into an unconstrained one using the method of objective function substitution method. It is tested with the typical test functions. The algorithm shows its superiority in handling the constrained conditions clearly compared with other constrained PSO algorithms. In order to verify the feasibility of the proposed constrained PSO algorithm applying in the engineering, the proposed algorithm is used to design aμ-PID fixed-structure robust controller by taking a sample missile longitudinal model for the classical Raytheon control structure. The simulated results indicate that the sample missile controller can not only satisfy a variety of time domain indexes but also have strong robustness, and the proposed algorithm is effective.

control and navigation technology of aircraft; air-to-air missile; particle swarm optimization; constrained optimization; robustness

2016-05-03

張民(1973—)，男，副研究員，博士。E-mail: zhangmin@nuaa.edu.cn

V249.122+.4

A

1000-1093(2017)01-0089-08

10.3969/j.issn.1000-1093.2017.01.012