GeoPMF:距離敏感的旅游推薦模型

張 偉 韓林玉 張佃磊 任鵬杰 馬 軍 陳竹敏

(山東大學計算機科學與技術學院 濟南 250101) (will_zhang2014@outlook.com)

GeoPMF:距離敏感的旅游推薦模型

張 偉 韓林玉 張佃磊 任鵬杰 馬 軍 陳竹敏

(山東大學計算機科學與技術學院 濟南 250101) (will_zhang2014@outlook.com)

雖然目前旅游者可以利用Web搜索引擎來選擇旅游景點，但往往難以獲得較好符合自身需要的旅游規劃.而旅游推薦系統是解決上述問題的有效方式.一個好的旅游推薦模型應具有個性化并能考慮用戶時間和費用的限制.調研表明，用戶在選擇旅游景點時，目的地與用戶常居地的距離常常是一個需要考慮的問題.因為旅行距離往往可以間接地反映了時間和費用的影響.于是，在貝葉斯模型和概率矩陣分解模型的基礎上，提出一個旅行距離敏感的旅游推薦模型(geographical probabilistic matrix factorization, GeoPMF).主要思想是基于每個用戶的旅游歷史，推算出一個最偏好的旅游距離，并作為一種權重,添加到傳統的基于概率矩陣分解的推薦模型中.在攜程網站的旅游數據集上的實驗表明，與基準方法相比，GeoPMF 的RMSE(root mean square error)可以降低近10%；與傳統概率矩陣分解模型(PMF)相比，通過考慮距離因子，RMSE平均降幅近3.5%.

旅游推薦；推薦系統；概率矩陣分解模型；距離敏感;GeoPMF算法

近年來，旅游已成為人們娛樂消遣的重要方式.據國家統計局網站發布的《2014年國民經濟和社會發展統計公報》①http://www.stats.gov.cn/tjsj/zxfb/201502/t20150226_685799.html顯示，2014年全年，我國出國游的人數達1億人次,國內游達36億人次.旅游已成為推薦系統[1]的重要應用領域之一.目前國內攜程、途牛和去哪兒網等旅游網站收集了大量的用戶反饋數據，為用戶對景點的選擇提供了依據.顯然，若能通過旅游推薦系統，為用戶提供更具個性化的推薦，將會極大地提高推薦系統的可用性.

關于旅游推薦已有不少工作.Ge等人[2]認為旅行花費對景點選擇有重要的影響，這里花費包括費用和時間.他們把旅行花費表示為一個時間，資金二元組.對于每個旅游者，都對應一個時間，資金二元組，用以表示用戶的預期偏好；對于每個景點，也有一個時間，資金二元組，視為每個景點的固有屬性.然后利用貝葉斯模型，將這2個二元組作為評分預測概率的先驗條件進行建模，給出旅游推薦.在結合地理因素方面，Tobler[3]在對基于位置的社交網絡(LBSN)的研究中，通過對用戶移動設備GPS信息的記錄，發現了一種簽到地點的空間聚類現象[3]，即個人游覽地點趨向于聚在一起.在興趣點(point-of-interest, POI)推薦的研究中，Ye等人[4]提出了一種結合用戶社交行為和地理因素的推薦模型，該模型是基于傳統的協同過濾算法中對相似度的計算，首先找到與用戶興趣最近鄰的K個用戶，將這K個用戶對該景點評分的加權平均作為評分的預測，只是在計算權值的時候結合了社交和地理信息.在考慮地理因素時，Ye等人通過分析Foursquare和Whrrl數據集，也發現了空間聚類現象.進一步地，Ye提出了一種指數模型來建模簽到概率與距離的關系，并利用簽到概率來計算新的權值.最終，該模型提高了興趣點推薦的準確率.然而，這種模型不能很好地解決數據稀疏性問題，當有新數據加入時，還要重新計算權值.而且該模型需要計算每個用戶去過的地點兩兩之間的距離，增大了計算量.Horozov等人[5]提出一種基于權重的矩陣分解模型來解決這一問題.在用戶特征向量和興趣點特征向量的基礎上，他們提出了用戶活動區域矩陣和興趣點影響力矩陣.指出興趣點的影響力表現在用戶到過某個景點再去周圍景點的概率，是一種與距離有關的二維正態分布形式.Horozov的模型是利用用戶的簽到信息，不包含用戶的反饋打分，初始待分解矩陣中的元素是用戶對每個景點的簽到頻次.

已有的研究大多是利用用戶對地點的簽到數據.利用簽到的頻次作為待分解的矩陣中的元素，或者將簽到與否描述為一個布爾變量，利用形成的0-1矩陣計算用戶相似度.這些方法利用的信息過少；在推薦上考慮用戶的反饋不足；之前基于距離的推薦大多是景點之間的實地距離，而不是景點與用戶之間的距離，個性化不強.針對上述問題，本文利用用戶常居地到各個景點的距離這一地理信息，結合貝葉斯模型[6-7]，提出一種針對旅游景點的推薦算法，即距離敏感的旅游推薦模型(geographical probabilistic matrix factorization, GeoPMF).其主要思想是基于每個用戶的旅游歷史，推算出一個最偏好的旅游距離，并作為一種權重添加到傳統的基于概率矩陣分解的推薦模型中.我們模型中的目標函數是一個具有連續性的凸函數，能夠利用隨機梯度下降快速地訓練模型.在攜程網站的旅游數據集上的實驗表明，與基準方法相比，GeoPMF 的RMSE(root mean square error)可以降低近10%；與傳統概率矩陣分解模型(PMF)相比，通過考慮距離因子，RMSE平均降幅近3.5%.

1 基于距離因子的旅游推薦模型

1.1 GeoPMF模型基本框架

較之于傳統的推薦領域，如電影[8-10]、音樂[11-13]、在線商店[14]，旅游推薦數據稀疏性問題更加嚴重.其主要原因在于用戶旅游的頻度較小.相對影視、音樂等活動，旅游的花費通常偏高，使得用戶旅游的次數大大低于傳統推薦領域的行為頻次.我們將攜程網站數據的統計結果與其他領域的數據集進行了對比分析，如表1所示.可以看出，對于前4個數據集，最稀疏的是Ciao數據集，其打分矩陣取值為空的元素占了99.97%;相比而言，攜程數據更加稀疏，僅是Ciao的40%.

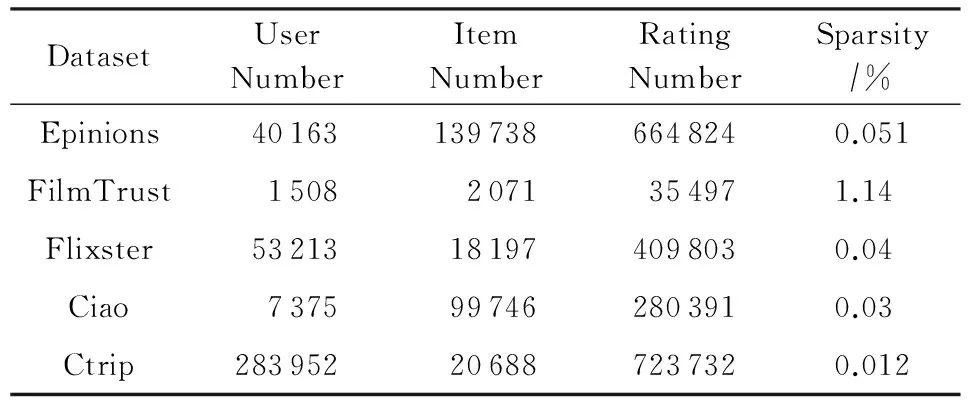
Table 1 The Sparsity Comparison Between Ctrip and

為了解決稀疏性問題，GeoPMF采用矩陣分解的思路，并將距離因素考慮進來.在選擇旅游景點時，用戶會考慮景點與自身所在地之間距離的可接受范圍.對于每一個用戶，我們將景點劃歸為不同的距離區段，比如在10 km范圍、10～20 km范圍等等，每一個距離區段用戶選擇的概率有差異；而且對每一個用戶來說，都有一個最偏好的距離區段.GeoPMF正是將這2個距離區段引入矩陣分解模型.圖1給出本模型的實現方法.首先，我們經過數據預處理操作，從攜程旅游數據中得到用戶對景點的打分矩陣；然后，利用百度LBS開放平臺根據景點地理信息獲得其GPS信息，并計算每個用戶-景點對之間的距離，得到距離區段矩陣；最后，將這2個矩陣作為GeoPMF模型的輸入，通過隨機梯度下降法訓練出模型參數，最終輸出用戶預測評分矩陣.

Fig. 1 The framework of GeoPMF model圖1 GeoPMF模型框架

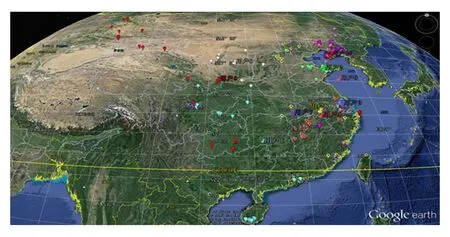
Fig. 2 Users’ tourism destination spots distribution on Ctrip website圖2 攜程網站不同用戶的旅游景點位置分布

1.2 距離對景點選擇影響的研究

本文在攜程網旅游數據中隨機選取了部分用戶，在地圖上標注他們的旅游目的地，結果如圖2所示.圖2中用不同顏色的圖標區分不同用戶的旅游歷史，圖釘用來標識用戶的常居地.這些信息都是從攜程網的旅游評論記錄中獲得.就旅游歷史與用戶常居地的相對距離來看，不同用戶的行為差異較大.有些用戶偏向僅去距離常居地較近的景點，如用戶2、用戶3和用戶10.而像用戶1、用戶9，卻偏向選擇較遠的景點.

基于對旅游行為的觀察，本文對該現象給出的解釋是，用戶選擇景點之前，首先對要去的距離區段有一個基本的定位.前面提到的Ye等人[4]利用指數模型對景點實地距離與選擇景點的概率進行了建模，但由于該模型本身具有計算概率值復雜、不能解決稀疏性等缺點，因此本文嘗試通過新的方式對二者關系進行建模.首先，基于上述解釋，我們認為景點所處的區段比實地距離更有考慮價值，鑒于此，在獲取用戶景點的經緯度信息后，我們計算出每個用戶與去過的景點的距離，然后按照10 km為單位為這些景點進行區段劃分.本文對不同區段內旅游數量統計處理，結果如圖3所示.橫坐標表示不同的距離區段，縱坐標是在每個區段內旅游頻數.從圖3中可以看出，用戶在不同區段內旅游頻次與距離區段有明顯相關性.

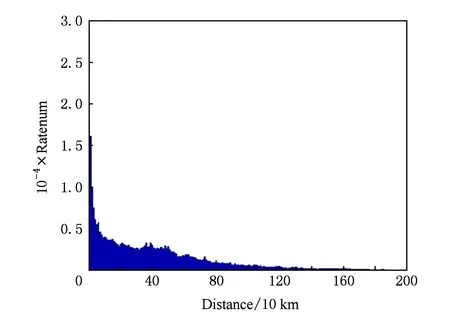
Fig. 3 The tourism frequency histogram in different distance sections圖3 不同距離區段內旅游頻次直方圖

然而，景點對用戶的吸引力不僅在于旅游頻次，還在于用戶的評分，用戶對景點的評分高低說明用戶對該景點的喜歡程度.為了描述用戶對不同區段景點的偏好，我們定義了一個概率函數，見式(1)：

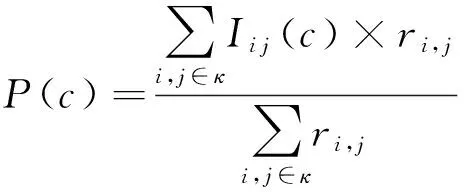
(1)

其中，c表示距離區段編號，以10 km為單位；κ表示用戶i去過的景點集合；Ii j(c)為指示函數，當景點j位于用戶i的第c個區段時為1，否則為0；ri j是用戶i對景點j的評分.我們用P(c)來估計用戶對不同距離區段的喜好程度.統計結果如圖4所示.橫坐標為不同距離區段;縱坐標表示用戶選擇該區段的概率，即P(c).從中看出，用戶對不同區段內景點的喜好程度與距離區段也存在明顯的相關性.而且，總體而言，用戶更喜好距離較近的景點.

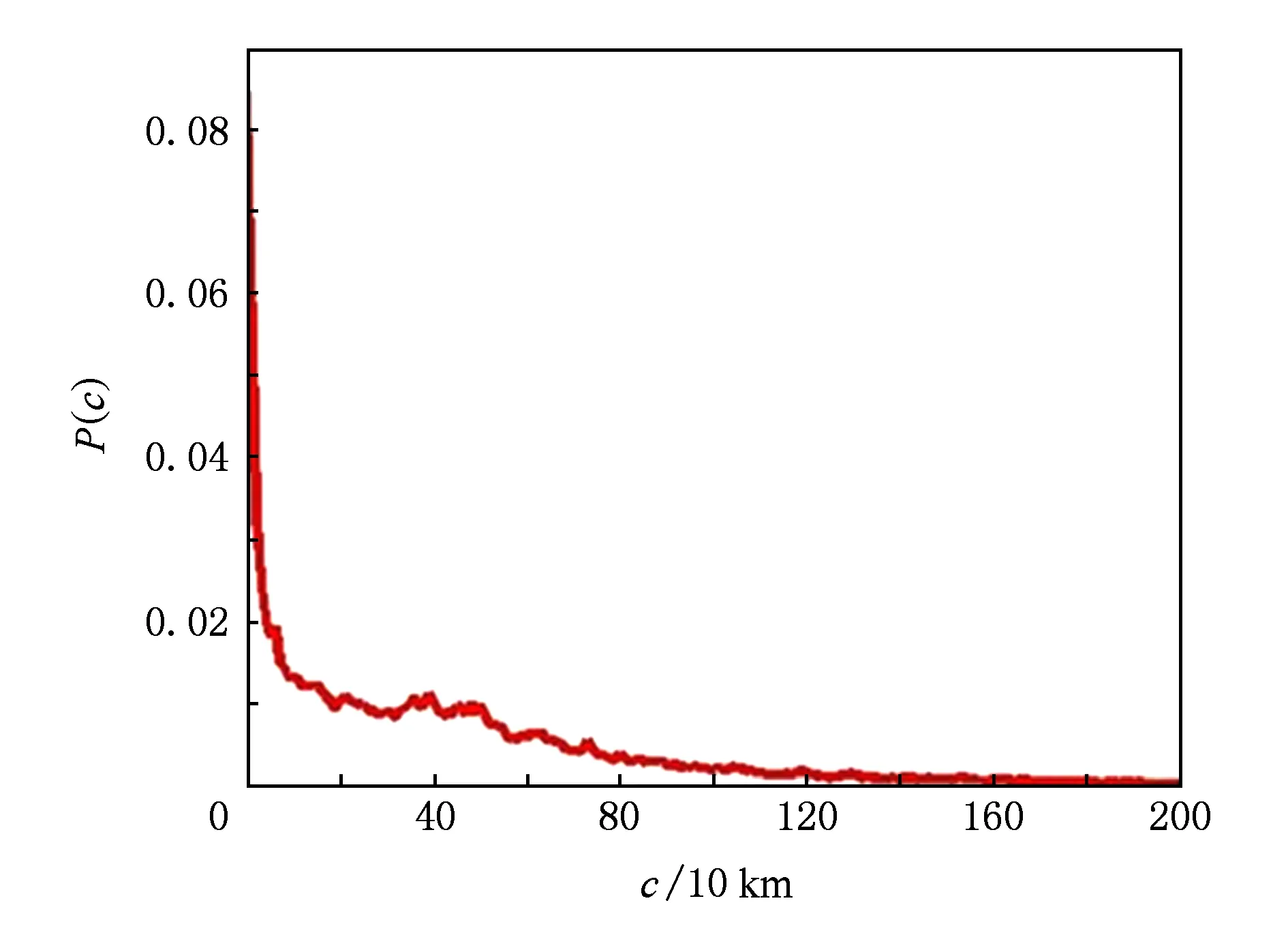
Fig. 4 The probability distribution of user preference with different tourist attractions圖4 用戶對不同景點偏好的概率分布

經過上述統計分析，我們得出結論：景點所處的距離區段不僅對用戶旅行目的地的選擇有重要影響，也間接地影響了用戶對去過景點的反饋評分.本文假設每個用戶在旅游的時候心中有一個最偏愛的距離區段即di，它與景點對應的距離區段Di j之間的偏差越小，用戶選擇的概率越大，給較高評分的概率也越大.因此，在1.3節中，我們將2個距離因子：用戶最偏愛的距離區段c和表示景點屬性的距離區段矩陣D作為考慮因素，建立一個對旅行距離敏感的旅游推薦模型GeoPMF.

1.3 GeoPMF模型的形式化

GeoPMF將景點相對于每個用戶所處的距離區段作為考慮因素.為此，本文引入距離區段矩陣D，其中每一個元素Di j表示相對于用戶i的常居地來說，景點j所處的距離區段.用戶i最偏愛的距離區段記為di.接著，我們將Si j引入到矩陣分解模型中.Si j表示用戶i最偏愛區段di與景點j所處區段Di j的相似度，取值范圍是[0,1].區別于傳統矩陣分解，我們對評分矩陣的分解見式(2)：

(2)

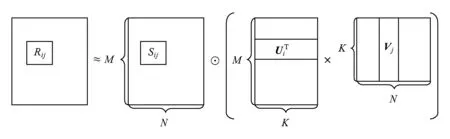
Fig. 5 Rating matrix decomposition of GeoPMF圖5 GeoPMF的評分矩陣分解

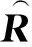
設評分的估計值與真實值之間存在誤差為ε，并假設ε服從高斯分布，則

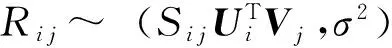
(3)

其中N(Ri j|μ,σ2)是滿足均值為μ、方差為σ2的高斯分布.

Si j的定義基于以下思想：對于用戶去過的景點，所處的距離區段Di j與di的差值會影響用戶的反饋評分，二者偏差越小，用戶給高分的可能性越大；對于用戶沒有去過的景點，Di j與di偏差越小，用戶選擇該景點作為旅游目的地的可能性也越大.因此，可采用歐氏距離來計算相似度，見式(4).對于每一個Si j，表示用戶最偏愛距離區段di與景點所處距離區段Di j的近似程度，值越大，二者越近似，用戶選擇該景點的概率越高.

Si j=S(di,Di j)=1-‖di-Di j‖2.

(4)

根據極大似然估計的思想，假設Ri j之間是獨立同分布的，我們得到用戶評分矩陣的似然函數為式(5)：

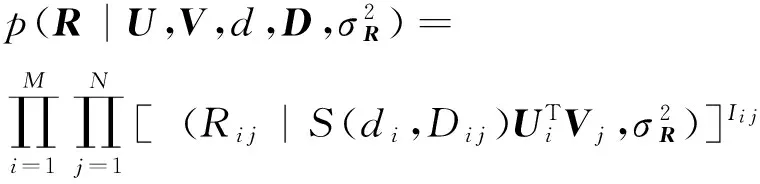
(5)

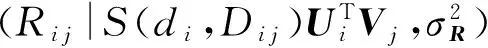
(6)

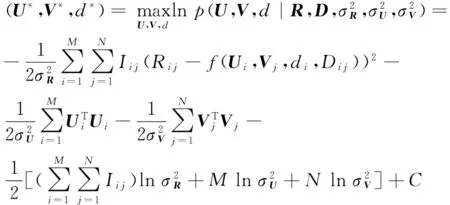
其中，C是一個與參數無關的常量.

使上述目標函數最大化，等價于最小化公式：

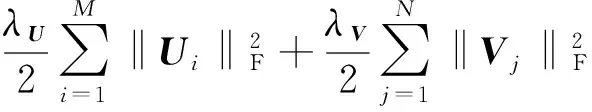
(7)

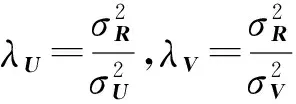
(8)

式(8)就是GeoPMF最終的目標函數.我們利用隨機梯度下降法(stochastic gradient descent, SGD)學習得到參數U，V，d.

GeoPMF的概率模型圖如圖6(b).較之于模型PMF(圖6(a))，本文在預測評分時，引入距離因子di和距離區段矩陣D.

2 實 驗

2.1 數據集

1) 攜程網旅游數據.本文實驗數據集采用攜程網旅游攻略的用戶評論信息.數據集包含用戶節點283 952個、景點節點20 688個、用戶打分723 732個，見表1所示.

2) 獲取地理信息.根據景點節點的名稱信息，使用百度地圖提供的開放API，生成景點以及用戶常居地的經緯度坐標.距離選取10 km為步長，每10 km表示一個區段.我們計算了每個用戶常居地到他去過的景點之間的距離，確定景點所屬的距離區段用以形成距離區段矩陣D.

3) 生成訓練集測試集.本文采用按時間分割的方式劃分測試集訓練集，見圖7所示.首先，去掉評論次數少于3條的用戶的所有評分數據；然后，按照每個用戶評論時間的順序對評分數據排序；最后，按照2∶1的比例將每個用戶前23的評分作為訓練集，剩余的作為測試集，并且對于訓練集中的每個用戶，保證在測試集中至少有一個評分數據.

經過數據處理，我們最終得到3個數據文件：訓練集文件(xctour_train.txt)、測試集文件(xtour_test.txt)和距離區段文件(distance_section.txt).訓練集和測試集所包含用戶數、景點數以及評分數等統計信息，見表2.距離區段文件保存了每個用戶去過的所有景點所屬的距離區段信息，共包含300 677個距離區段數據.

Fig. 7 Preprocessing on Ctrip dataset圖7 攜程數據集預處理

DatasetFileSize∕MBUserNumberSiteNumberRatingNumberorSectionNumberMinScoreorMinDistanceMaxScoreorMaxDistanceSetRatio∕%TrainingSet2.4631408171771935411564.37TestSet1.3731408204511071361535.63SectionFile4.0731408205883006770458

2.2 基準方法

1) GlobalAverage.用戶評分矩陣所有真實值的平均值作為評分預測值.

2) ItemAverage.對某一景點的評分等于該景點收到的所有評分的平均值.

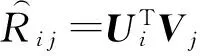
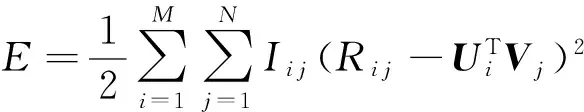
SVD是一種最基本的矩陣分解模型.

4) PMF.由Salakhutdinov等人[16]首先提出，其概率模型圖見圖6(a).他假設預測評分與真實評分之間存在高斯噪聲，并假設U,V滿足均值為0的高斯分布.最終得到的損失函數為式(10)：

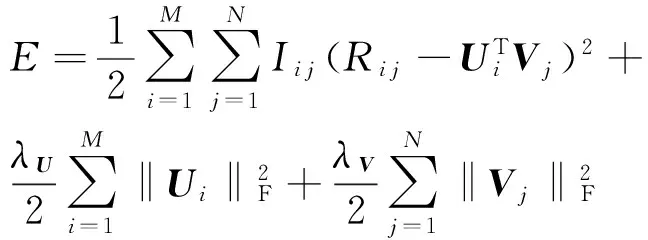
5) SocialMF.由Jamali和Ester[17]提出，將社交網絡中的信任關系結合到矩陣分解中，其目標函數形式為式(11)：

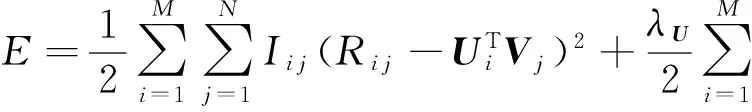
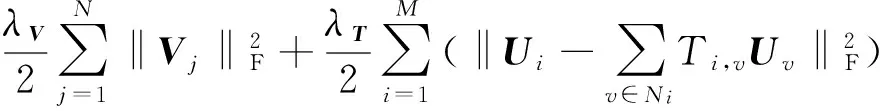
其中,T表示信任關系矩陣，當用戶v關注用戶i時，Ti,v=1;Ni表示用戶i所關注的其他用戶的集合.通過加入信任關系這一特征，Jamali和Ester通過實驗證明該方法能顯著降低RMSE.在攜程旅游數據中也能夠取得用戶之間的關注信息，而且GeoPMF和SocialMF都是以矩陣分解為基礎，區別在于選取的上下文信息以及建模形式不同，因此我們將SocialMF也作為比較對象進行實驗.

上述所有的推薦算法都在我們處理過的攜程訓練集xctour_train.txt上進行實驗.

2.3 評價指標

在推薦領域，評價一個推薦算法預測評分的好壞，常用的評價指標是RMSE，用來表示估計評分的誤差，定義為式(12)：

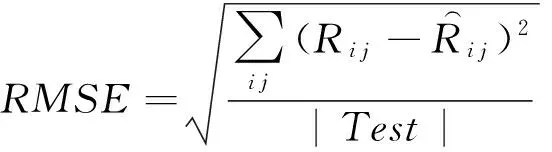
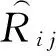
2.4 參數設置

PMF，SVD正規項λU=λV=0.001，GeoPMF正規項設置為λU=λV=0.01.d的每一項利用景點距離區段均值進行初始化，即di初值為D對應行向量元素的均值.矩陣U,V中元素取值服從均值為0、標準差為0.1高斯分布.

2.5 結果比較

1) GeoPMF與基準方法及傳統矩陣分解的比較.考慮特征向量Ui和Vj的維數K，即潛在因子數會對結果造成影響，我們設置了不同的特征向量維數進行實驗，得到圖8中的結果.最下面的一條線是GeoPMF的結果.總體來看，矩陣分解方法要比基準方法效果好.基準方法GlobalAverage和ItemAverage是直接利用均值進行預測，所以RMSE并不發生變化，在圖8中表現為直線.而PMF和SVD區別僅在于正規項的加入，所以2條曲線幾乎一致.在每個維度下，GeoPMF的結果都要優于其他方法.橫向來看，對于GeoPMF，SocialMF，SVD來說，隨著特征向量維數的增加，RMSE先減少后增加，均在維數為5達到最優.隨著特征向量維數的增加，GeoPMF的結果與PMF和SVD之間差距逐漸增大.當特征向量維數為5時，RMSE降低幅度近1%，在達到穩定狀態時，RMSE降低幅度達到5%.SocialMF的RMSE在特征向量維數為5時達到最優，但最優值也要稍差于GeoPMF，且維數繼續增加時，RMSE劇烈升高，SocialMF實驗結果惡化.最終實驗結果顯示，較之于基準方法，GeoPMF的RMSE平均降幅為9%，最優值降幅為10%；較之于矩陣分解方法PMF和SVD，RMSE平均降幅為3.5%，最優值降幅為1%.

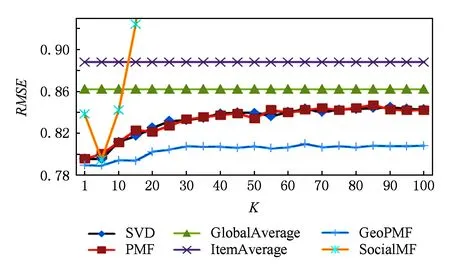
Fig. 8 Impact of dimensionality K on RMSE圖8 特征向量維數K對RMSE的影響

雖然從上述實驗結果我們看到GeoPMF模型的優越性，但是為了驗證GeoPMF實驗結果是真正優于基準方法，還是因為優化過程的隨機初始化等導致的性能提高，本文對圖8中實驗結果進行了顯著性檢驗[18].我們對PMF和GeoPMF的實驗數據進行顯著性分析，表3是對2組數據進行獨立T檢驗的結果.從結果中看出，顯著性為0.005，說明二者方差存在顯著性差異，在方差不等的情況下，雙尾顯著性為0.000;而當顯著性小于0.05時，認為配對樣本之間存在顯著差異，即后測與前測之間存在顯著差異，說明GeoPMF對于RMSE的降低效果顯著.

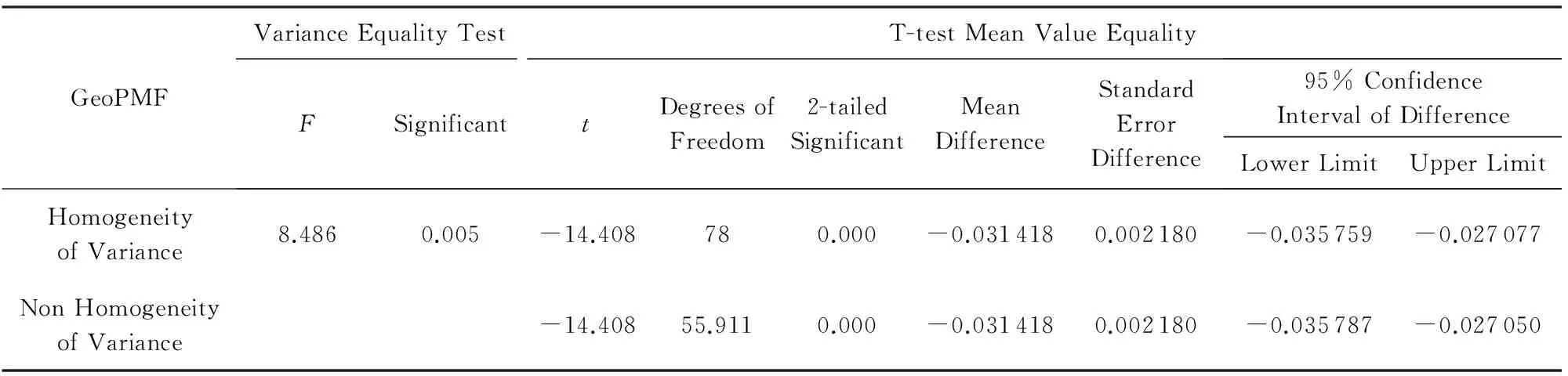
Table 3 T-test Result in SPSS表3 SPSS T-檢驗結果

接著，我們比較不同算法RMSE隨迭代次數的變化.根據上述實驗結果，我們將特征向量維數固定于5.實驗結果如圖9所示.從圖9可看出，GeoPMF效果也要優于其他推薦算法，當算法收斂時，RMSE達到0.79，較之于基準方法和PMF分別有10%和1%的提高，并且也稍優于SocialMF方法.總體來看，隨著迭代次數的增加，GeoPMF的RMSE不斷降低，收斂后較之于PMF和SVD，更加穩定.另外，可以看出，而SVD由于沒有引入正規項，當迭代次數達到30時，RMSE出現上升趨勢，說明存在過擬合現象.

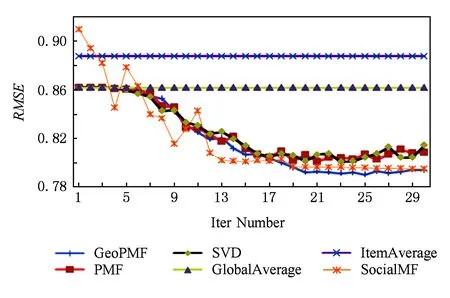
Fig. 9 Impact of iter number on RMSE (K=5)圖9 迭代次數對RMSE的影響(K=5)

2) 距離區段可視化.d是在模型假設中定義的區段向量，其中的每一個元素di代表用戶最偏好距離。我們通過隨機梯度下降學習矩陣U，V的同時，也學習得到d.為了直觀地展示距離區段這一距離因子，我們對d的學習結果和用戶已經去過的景點區段進行了可視化分析，如圖10所示.橫坐標表示隨機選取的13位用戶.每一位用戶對應縱軸的一列散點集合，我們用Du表示與用戶對應的一列點集.其中，每一列的每一個星型符號表示用戶去過的景點所屬距離區段即Di j，菱形表示GeoPMF模型學習得到的用戶最偏好區段di.注意，在訓練開始前，d中元素是用D中對應的每一行距離區段均值進行初始化的.從圖10中看出，在訓練結束后，菱形落在星型符號集中分布的區域周圍，即d更加靠近用戶最常去的距離區段，這與人們的經驗一致.

3) 模型效率.表4是對矩陣分解算法運行時間的統計結果.從表4可看出，GeoPMF運行時間較之于PMF和SVD有所增加.由于算法引入距離區段矩陣，并且在學習過程中要同時學習距離區段向量d，使得性能相對PMF和SVD來說有所降低.但這種運行時間的增加相對于RMSE的降低來說是在可接受范圍之內的.而SocialMF的運行時間較之于GeoPMF增加了近3倍，且從前面的實驗結果看，GeoPMF的實驗結果也要稍優于SocialMF，這也更加體現了GeoPMF的優越性.

Table 4 The Runtime of Recommendation Algorithms表4 推薦算法運行時間

3 總結及未來工作

本文中，我們對攜程網旅游數據進行統計分析，證明景點所處的距離區段在旅游目的地選擇中是一個重要的考慮因素.據此，我們提出了一種基于距離因子的旅游推薦模型GeoPMF，從矩陣分解的角度研究了旅游推薦算法，目的是降低評分估計誤差.我們結合PMF，將用戶最偏愛距離區段和景點實際所處的距離區段作為考慮條件，納入概率分解模型.這樣做的好處是，我們就既考慮用戶對景點本身的偏好，同時考慮了用戶對距離區段的偏好.在最終的實驗結果中，RMSE降低到0.79.通過與基準方法的比較，證明了GeoPMF對降低RMSE有顯著效果.同時，GeoPMF對用戶旅游景點的選擇上也有一定指導意義.

在未來的工作中，我們會將GeoPMF應用于其他旅游網站的數據以及其他包含地理信息的數據集，用來驗證該模型的適應性.另外，我們的GeoPMF也有一定局限性，首先，我們模型選擇用戶的常居地是一個定值，在現實生活中，用戶的地理位置往往伴隨著遷徙行為，比如一個用戶常居地從一個省份到另一個省份；其次，當用戶到達一個景點進行旅游時，常常會對所在目的地的周邊景點也產生興趣.另外，除了考慮物理距離，還應考慮交通的便利性.對于以上情況，我們會以GeoPMF為基礎，結合景點選擇中的各種影響因素，提出一種更具泛化能力的模型，為旅游者的行程做出更好的規劃.

[1]Adomavicius G, Tuzhilin A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions[J]. IEEE Trans on Knowledge and Data Engineering, 2005, 17(6): 734-749

[2]Ge Y, Liu Q, Xiong H, et al. Cost-aware travel tour recommendation[C] //Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 983-991

[3]Tobler W. A computer movie simulating urban growth in the detroit region [J]. Economic Geography, 1970, 46: 234-240

[4]Ye M, Yin P, Lee W C, et al. Exploiting geographical influence for collaborative point-of-interest recommendation [C] //Proc of the 34th ACM SIGIR Int Conf on Research and Development in Information Retrieval. New York: ACM, 2011: 325-334

[5]Horozov T, Narasimhan N, Vasudevan V. Using location for personalized poi recommendations in mobile environments [C] //Proc of the Int Symp on Applications Internet. Los Alamitos, CA: IEEE Computer Society, 2006: 625-636

[6]Ji Junzhong, Liu Chunnian, Sha Zhiqiang. Bayesian belief network model learning, inference and applications [J]. Computer Engineering and Applications 2003, 39(5): 24-27 (in Chinese)(冀俊忠, 劉椿年, 沙志強. 貝葉斯網模型的學習、推理和應用[J]. 計算機工程與應用, 2003, 39(5): 24-27)

[7]Cheng Lanlan, He Pilian, Sun Yueheng. Study on Chinese keyword extraction algorithm based on naive Bayes model [J]. Journal of Computer Applications, 2005, 25(12): 2780-2782 (in Chinese)(程嵐嵐, 何丕廉, 孫越恒. 基于樸素貝葉斯模型的中文關鍵詞提取算法研究[J]. 計算機應用, 2005, 25(12): 2780-2782)

[8]Lekakos G, Caravelas P. A hybrid approach for movie recommendation [J]. Multimedia Tools & Applications, 2008, 36(1/2): 55-70

[9]Biancalana C, Gasparetti F, Micarelli A, et al. Context-aware movie recommendation based on signal srocessing and machine learning [C] //Proc of the 2nd Challenge on Context-Aware Movie Recommendation. New York: ACM, 2011: 5-10

[10]Mirza B J, Keller B J, Ramakrishnan N. Studying recommendation algorithms by graph analysis [J]. Journal of Intelligent Information Systems, 2003, 20(2): 131-160

[11]Cano P, Koppenberger M, Wack N. Content-based music audio recommendation[C] //Proc of the 13th Annual ACM Int Conf on Multimedia. New York: ACM, 2005: 211-212

[12]Chen H, Chen A L P. A music recommendation system based on music data grouping and user interests [C] //Proc of the 10th Int Conf on Information and knowledge Management. New York: ACM, 2001: 231-238

[13]Li Ruimin, Lin Hongfei, Yan Jun. Mining latent semantic on user-tag-item for personalized music recommendation [J]. Journal of Computer Research and Development, 2014, 51(10): 2270-2276 (in Chinese)(李瑞敏, 林鴻飛, 閆俊. 基于用戶-標簽-項目語義挖掘的個性化音樂推薦[J]. 計算機研究與發展, 2014, 51(10): 2270-2276)

[14]Lee K C, Kwon S. Online shopping recommendation mechanism and its influence on consumer decisions and behaviors: A causal map approach[J]. Expert Systems with Applications, 2008, 35(4): 1567-1574

[15]Koren Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model [C] //Proc of the 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2008: 426-434

[16]Salakhutdinov R, Mnih A. Probabilistic matrix factorization[C/OL] //Proc of the Advances in Neural Information Processing Systems. 2007: 1257-1264 [2015-11-16]. http: //papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf

[17]Jamali M, Ester M. A matrix factorization technique with trust propagation for recommendation in social networks[C] //Proc of the 4th ACM Conf on Recommender Systems. New York: ACM, 2010: 135-142

[18]Zhou Yuzhu, Jiang Fenghua. The regression analysis of the experimental DATAS and the remarkable examination [J]. Physical Experiment of College, 2001, 14(4): 43-46 (in Chinese)(周玉珠, 姜奉華. 實驗數據的一元線性回歸分析及其顯著性檢驗[J]. 大學物理實驗, 2001, 14(4): 43-46)

Zhang Wei, born in 1993. PhD candidate in Shandong University. Student member of CCF. His main research interests include information retrieval, tweet summarization and recommender system.

Han Linyu, born in 1992. Master candidate in Shandong University. Student member of CCF. Her main research interests include information retrieval, Web data mining and recommender systems(zhangdianlei11@gmail.com).

Zhang Dianlei, born in 1993. Master candidate in Shandong University. Student member of CCF. His main research interests include information retrieval, data mining and recommender systems(zhangdianlei11@gmail.com).

Ren Pengjie, born in 1990. PhD candidate in Shandong University. Student member of CCF. His main research interests include information retrieval, data mining.

Ma Jun, born in 1956. Professor and PhD supervisor in Shandong University. Senior member of CCF. His main research interests include information retrieval, data mining, parallel computing, natural language processing.

Chen Zhumin, born in 1977. Associate professor and master supervisor in Shandong University. Senior member of CCF. His main research interests include Web information retrieval, data mining, and social computing(chenzhumin@sdu.edu.cn).

GeoPMF: A Distance-Aware Tour Recommendation Model

Zhang Wei, Han Linyu, Zhang Dianlei, Ren Pengjie, Ma Jun, and Chen Zhumin

(SchoolofComputerScienceandTechnology,ShandongUniversity,Jinan250101)

Although people can use Web search engines to explore scenic spots for traveling, they often find it very difficult to discover the sighting sites which match their personalized need well. Tour recommendation systems can be used to solve the issue. A good tour recommendation system should be able to provide personalized recommendation and take the time and cost factors into account. Furthermore, our investigation shows that often a useruwill consider the distance between herhis habitual residence and the tour destination when shehe makes herhis travel plan. It is because that the travel distance reflects the effect of time and cost indirectly. Therefore, we propose a distance-aware tour recommendation model, named GeoPMF (geographical probabilistic matrix factorization), which is developed based on the Bayesian model and PMF (probabilistic matrix factorization). The main idea of GeoPMF is that for each user we try to get a most preferred travel distance span by mining her past tour records. Then we use it as a kind of weight factors added into the traditional PMF model. Experiments on travel data of Ctrip show that, our new method can decreaseRMSE(root mean square error) nearly 10% compared with some baseline methods. And when compared with the traditional PMF model, the average decline onRMSEis nearly 3.5% in virtue of the distance factor.

tour recommendation; recommender system; probabilistic matrix factorization (PMF) model; distance-aware; GeoPMF

2015-09-15；

2015-12-22

國家自然科學基金項目(61272240,61672322)；山東省自然科學基金項目(ZR2012FM037)；微軟國際合作基金項目(FY14-RES-THEME-25) This work was supported by the National Natural Science Foundation of China(61272240,61672322), the Natural Science Foundation of Shandong Province(ZR2012FM037), and the Microsoft International Cooperation Fund Project (FY14-RES-THEME-25).

馬軍(majun@sdu.edu.cn)

TP301