求概率的常見錯誤分析

/

求概率的常見錯誤分析

文/王友峰

概率是中考的必考內容.下面以中考題為例，把求概率的常見錯誤歸納如下，以助你避免重蹈覆轍.

一、不能準確判斷事情的種類

例1（2016年天水卷）下列事件中，必然事件是（）

A.拋擲1枚骰子，6點朝上.B.兩條直線被第三條直線所截，同位角相等.

C.366人中至少有2人的生日相同.D.實數的絕對值是非負數.

錯解：選C.

錯因診斷：對于C中的事件，錯解認為一年365天，按照抽屜原理，將366人放到365個“抽屜”中，至少有一個“抽屜”中有2個人，因此它是必然事件.沒有考慮閏年有366天的特殊情況.

正解：實數的絕對值一定是非負數．選D．

二、不能正確理解概率的含義

例2（2016年常德卷）下列說法正確的是（）

A.袋中有形狀、大小、質地相同的5個紅球和1個白球，隨機取出一個球，一定是紅球.

B.天氣預報“明天降水概率是10%”，是指明天有10%的時間會下雨.

C.發行一種福利彩票，中獎概率是千分之一．那么，買這種彩票1000張一定會中獎.

D.連續擲一枚均勻硬幣，若5次都是正面朝上，則第六次仍然可能正面朝上.

錯解：選B或C.

錯因診斷：“明天降水概率是10%”表示明天降雨的可能性為10%，而不是有10%的時間會下雨，因此B不正確；彩票中獎的概率是千分之一表示彩票中獎的可能性為1‰，買1000張彩票不一定會中獎，因此C不正確.正解：投擲硬幣是隨機事件，第六次仍然可能正面朝上.選D．

三、沒有理解可能性與概率的關系

例3（2016年福州卷）下列說法中，正確的是（）

A.不可能事件發生的概率為0.

C.概率很小的事件不可能發生.

D．投擲一枚質地均勻的硬幣100次，正面朝上的次數一定為50次.

錯解：選B或C.

錯因診斷：隨機事件可能發生，也可能不發生，但發生與不發生的可能性不一定相同，所以B選項錯誤；概率很小的事件也可能發生，只是發生的可能性較小，所以C選項錯誤.

正解：不可能事件發生的概率為0，A選項正確；由上可知，B、C選項不正確；投擲一枚質地均勻的硬幣100次，正面朝上的次數可能為50次，也可能不是50次，D選項錯誤.選A.

四、畫錯樹狀圖

圖1

例4（2016年泰州卷）一只不透明袋子中裝有1個紅球、2個黃球，這些球除顏色外都相同.小明攪勻后從中任意摸出一個球，記錄顏色后放回、攪勻，再從中任意摸出一個球.用樹狀圖或列表法表示摸出球的所有等可能情況，并求兩次摸出的球都是紅色的概率．

圖2

錯因診斷：錯解沒有考慮紅球和黃球的個數不同這個隱含條件．

正解：把2個同一顏色的黃球編號為黃1和黃2，畫樹狀圖如圖2所示，兩次摸出的都是紅球的概率為

五、分不清放回與不放回

例5（2016年臨沂卷）某校九年級共有1、2、3、4四個班，現從這四個班中隨機抽取兩個班進行一場籃球比賽，則恰好抽到1班和2班的概率是（）

錯解：列表如下：

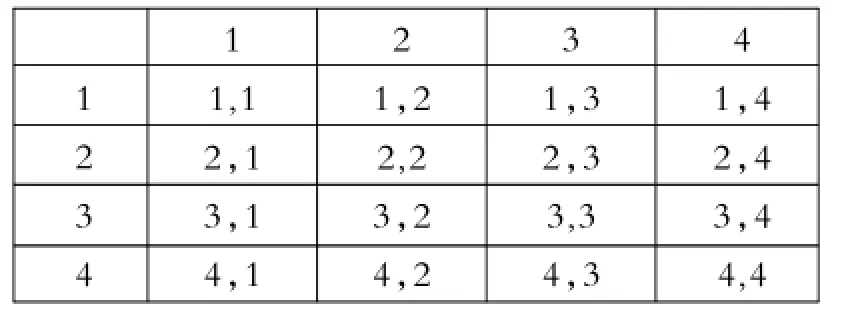
1 2 3 4 1 1 , 1 2，1 3，1 4，1 2 1，2 2 , 2 3，2 4，2 3 1，3 2，3 3 , 3 4，3 4 1，4 2，4 3，4 4 , 4

錯因診斷：本班不能與本班進行比賽，在表格中，不能出現相同的數字.正解：列表如下：

1 2 3 4 1 --2，1 3，1 4，1 2 1，2 --3，2 4，2 3 1，3 2，3 --4，3 4 1，4 2，4 3，4 --

六、考慮不周導致解答不完整

例6三人相互傳球，由甲開始發球，并作為第一次傳球．（1）用列表或畫樹狀圖的方法求經過3次傳球后，球回到甲的概率是多少？

（2）由（1）進一步探索：經過4次傳球后，球回到甲的傳球方法共有多少種？

（3）就傳球次數與球分別在甲、乙、丙手中的可能性大小，提出你的猜想（寫出結論即可）．

錯因診斷：（1）、（2）都正確；（3）錯解由于缺少分類意識，考慮不周而導致答案不完整.

（2）畫樹狀圖如圖4所示，經過4次傳球后，球在甲手中的傳球方法共有6種.

（3）猜想：當n為奇數時，

圖3

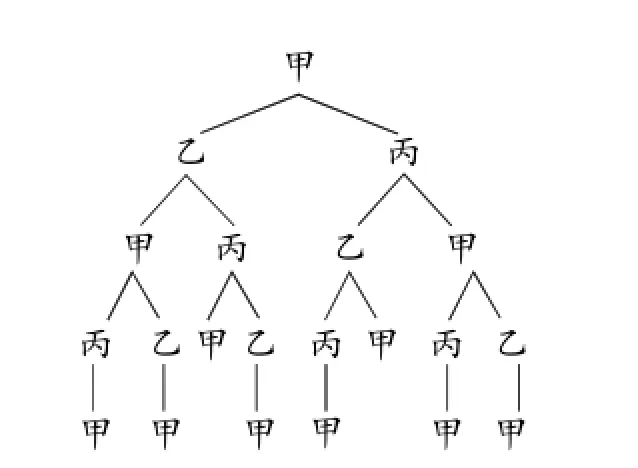
圖4