基于PSO的工業機器人時間-脈動最優軌跡規劃

沈 悅，李銀伢， 戚國慶，盛安冬

(南京理工大學 自動化學院，江蘇 210094)

基于PSO的工業機器人時間-脈動最優軌跡規劃

沈 悅，李銀伢， 戚國慶，盛安冬

(南京理工大學 自動化學院，江蘇 210094)

為提高工業機器人的工作效率，并且保持機器人關節平穩運動，提出一種基于粒子群優化算法的時間-脈動最優軌跡規劃方案；通過權重法將多目標優化轉化為單目標優化，再運用粒子群優化算法得到時間-脈動最優的運動軌跡；軌跡規劃中，采用了關節空間五次非均勻B樣條插值法，以確保脈動曲線的連續性；最后以GRB4016工業機器人為研究對象進行仿真實驗，結果表明，該方案可以得到較理想的運動軌跡，并驗證了方案的有效性。

B樣條曲線；粒子群優化；時間-脈動最優；軌跡規劃

0 引言

工業機器人的軌跡規劃是軌跡跟蹤控制的基礎，對工業機器人的工作效率、平穩運動、能量消耗等均具有重要意義，所規劃的軌跡函數都必須是連續和平滑的，從而使得工業機器人能平穩的運動。工業機器人的軌跡規劃可分為笛卡爾空間(也即工作空間)軌跡規劃和關節空間軌跡規劃[1-2]，笛卡爾空間軌跡規劃能夠直觀的觀察到工業機器人末端的運動軌跡及其位姿，但是，這種方法不能回避運動學奇異點的問題，從而給運算帶來了很大的麻煩；而關節空間的軌跡規劃方法則不存在這種問題。本文主要探討的是關節空間的軌跡規劃方法。如今，關節空間的軌跡規劃方法常用的有拋物線過渡的線性插值法[1-2]、多項式插值法[3-4]、B樣條插值法[5]等插值法，和從加速度曲線出發的矩形加速度曲線法、梯形加速度曲線法、正弦加速度曲線法及其組合法等[6]。其中，多項式插值具有階次高、沒有凸包性的缺點；矩形加速度法具有加速度曲線不連續的缺點；梯形加速度法具有加加速度曲線不連續的缺點；而B樣條曲線可以分段處理、具有局部支撐性、凸包性和導數連續性，應用廣泛，效果明顯優于其他插值法。

關節空間規劃的軌跡優化[7]根據性能指標劃分可分為時間最優[8-9]、脈動(即加加速度)最優[10-11]、能量最優[9]、距離最短等，其中時間最優算法是最早提出的。優化方法大多采用免疫算法[8]、遺傳算法[12]、粒子群算法等進化算法，以及上述算法的改進或混合算法。近年來，粒子群優化算法(PSO，particle swarm optimization)得到諸多研究學者的關注。相較于遺傳算法，粒子群算法具有參數設置簡單、易調節，算法簡單、易實現等優勢。

B樣條曲線具有局部支撐性、凸包性以及導數連續性等優點，而粒子群算法則具有參數設置簡單、易調節，算法簡單、易實現等優勢。因此，為提高工業機器人的工作效率，并且保持機器人平穩運動，本文提出一種基于PSO(particle swarm optimization)算法的五次B樣條插值的工業機器人軌跡規劃方法。具體的，先預設關節路徑點，再進行五次B樣條插值，得到C4連續的軌跡曲線，以確保脈動函數(即加加速度jerk函數)連續；然后運用PSO算法，以路徑點之間的時間間隔序列為粒子向量，考慮約束條件(速度、加速度、加加速度等)，最終達到優化的目的。

1 問題描述

關節空間點到點(PTP，PointtoPoint)軌跡規劃，即根據工作任務，得到一系列工作空間機械臂末端的期望路徑點，再根據逆運動學運算得到關節空間相應的關節角，最后對所得關節角路徑點進行插值運算，以關節角的函數來描述軌跡(時間和空間)。

圖1 GRB4016工業機器人模型

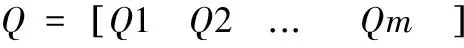
(1)

相應的速度、加速度、加加速度(脈動)函數表示如下：

(2)

(3)

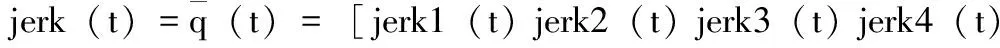
jerk5(t)jerk6(t)]T

(4)

進行軌跡優化過程中，為實現工業機器人關節空間軌跡規劃的優化，從機器人的運行效率和軌跡平滑性出發，定義如下性能指標：

(5)

(6)

上式中，S1為機器人關節軌跡運行總時間，也可用tall或tm表示，用來衡量機器人運行效率，m為預設路徑點個數，i為路徑點序號；S2為機器人關節平均脈動，用來衡量機器人軌跡平滑性，其中，N為關節數，本文N=6，j為關節序號，jerkj(t)為j關節的脈動函數，可由式(4)求得。

2 五次B樣條函數構造

本文在關節空間運用非均勻B樣條對關節路徑點進行插值，第j關節第i段k次非均勻B樣條插值的軌跡可描述為：

(7)

式(3)中Vj,r為j關節的控制點，共有1+k個控制點來定義該段軌跡，那么m-1段軌跡則有m-1+k個控制點，上述控制點可由已知路徑點反求得到；Br,k(u)為k次規范B樣條基函數，其每一個可稱為規范B樣條，有如下定義[5,13]：

(8)

(9)

為下文進一步分析軌跡的速度、加速度、加加速度曲線以及邊界條件，利用下式可遞推求得相應的階控制點，進而得到軌跡的階導數[13]：

(10)

本文中預期得到脈動(加加速度)連續的軌跡，采用了C4連續的非均勻五次B樣條插值法，因此得到的軌跡也是C4連續的。將k=5代入上述相關公式進行運算，針對j關節進行求解。對m+4個控制點進行反求，需要列出m+4個方程，其中m個方程可由已知路徑點列出：

(10)

(11)

最后可列出矩陣方程

AjDj=Pj，解得Dj=Aj-1Pj

(12)

3 基于PSO的最優時間-脈動求解

根據第1章節中定義的性能指標，將時間-脈動最優這一多目標優化，運用權重法轉化為單目標優化，得到算法所需的適應度函數如下：

fit=a·S1+b·S2

(13)

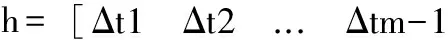
基本粒子群算法的描述及其各項參數定義如下[14-15]：

(14)

式(12)中參數按經驗選取：加速因子c1=1.49,c2=1.49，慣量因子ω=0.729，r1,r2為[0,1]之間的隨機數。pidk為粒子個體位置最優值，pgdk為群體位置最優值。

基于PSO的五次B樣條軌跡規劃方案的具體步驟如下：

1)根據經驗初始化粒子群規模N，慣性因子，加速因子等，一般地，N=20；

3)根據式(14)來更新粒子的速度向量和位置向量，超出搜索范圍的用該維數的最大值或最小值代替；

4)根據式(13)計算粒子當前位置的適應值，更新粒子歷史最優位置pidk和群體最優位置pgdk；

5)若滿足優化條件則停止迭代；由于本文所求沒有優化條件，需設置最大迭代次數DTMax，以確保算法達到收斂狀態，若未達到最大迭代次數，則需返回步驟③。

4 仿真與實驗結果分析

為驗證基于PSO的五次非均勻B樣條曲線插值軌跡規劃方案的有效性，即能得到運行時間S1較短、加加速度(脈動)曲線連續以及平均脈動S2較小的軌跡，并且探討將多目標優化轉化為單目標優化的適應度函數中S1、S2的權重系數的取值對上述兩種指標優化結果的影響，本文以GRB4016型六自由度工業機器人為研究對象，如圖1所示，其各軸運動范圍和運動約束(見表1)，預設8個路徑點(見表2)，在關節空間進行基于PSO算法的五次非均勻B樣條軌跡規劃。

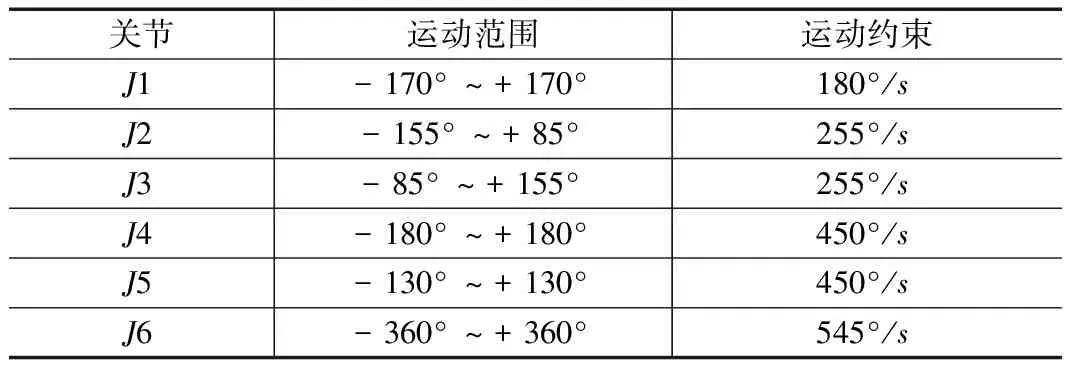
表1 軸運動范圍及約束

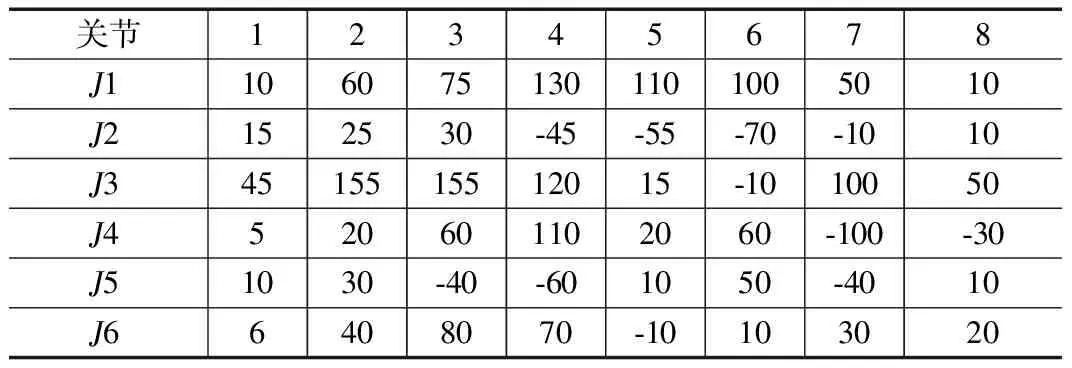
表2 關節路徑點 (單位：度)

在進行五次非均勻B樣條軌跡規劃時，需進行7段軌跡的規劃，時間序列長度為7。則運用PSO算法進行優化中，粒子的維數為7，設有20個粒子，DTMax設為100，加速因子、慣性因子等其他參數均按第三章所述設定，再設定不同的權重系數值a,b(a+b=1)，最后進行多次仿真實驗得到時間-脈動優化的結果如表3。

表3 基于PSO的時間-脈動優化時間序列及性能指標

由表3可知，a的值越大，權重就越大，S1就值越小，表明優化效果越明顯；同理，b的值越大，權重越大，S2值越小，其優化效果越明顯。其中對于變化幅度而言，隨著a的減小，相較于指標S1的增加的幅度，指標S2的下降的幅度較大，說明權重變化對指標S2的影響較大。具體的，a=1時，S1指標值(即工業機器人運行時間總和)可以達到一個較小的值，但由于沒有對S2(即加加速度平均值)進行優化，S2數值較大；當S2的比例大于0.05，其值就基本穩定在幾十的范圍內，因此結合指標S1，選取加權指標較小的第三組數據(a=0.9,b=0.1)進行五次非均勻B樣條插值，從而得到各關節的位置曲線(關節角變量曲線)、角速度曲線、角加速度曲線、角加加速度(脈動)曲線，如圖2～圖5所示。

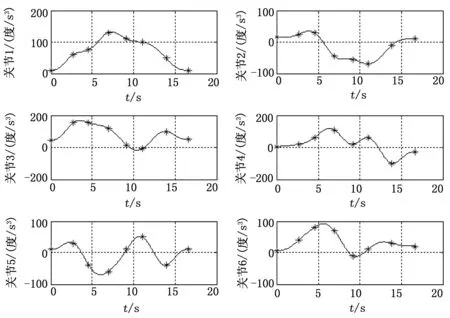
圖2 各關節位置曲線及路徑點

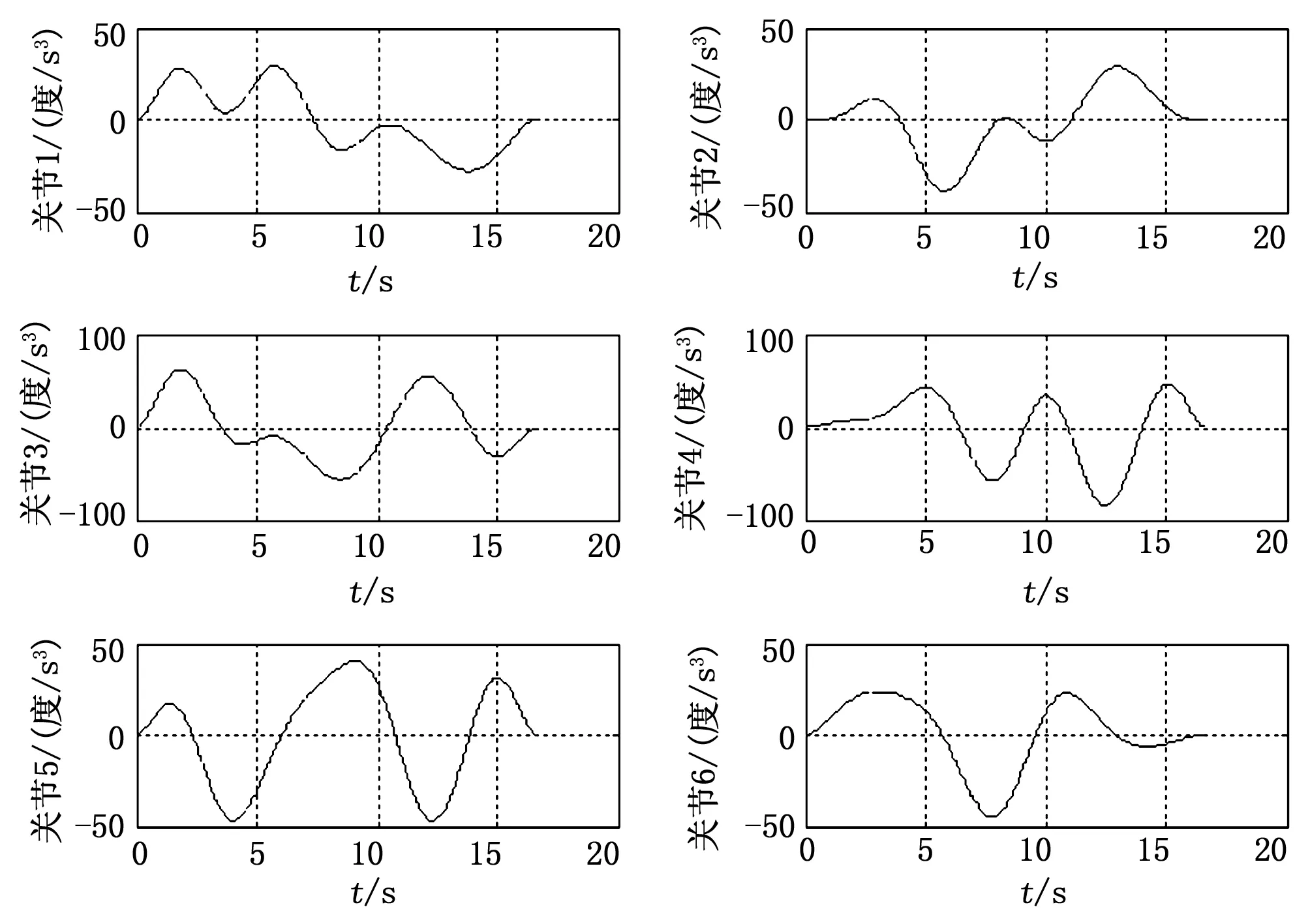
圖3 各關節角速度曲線

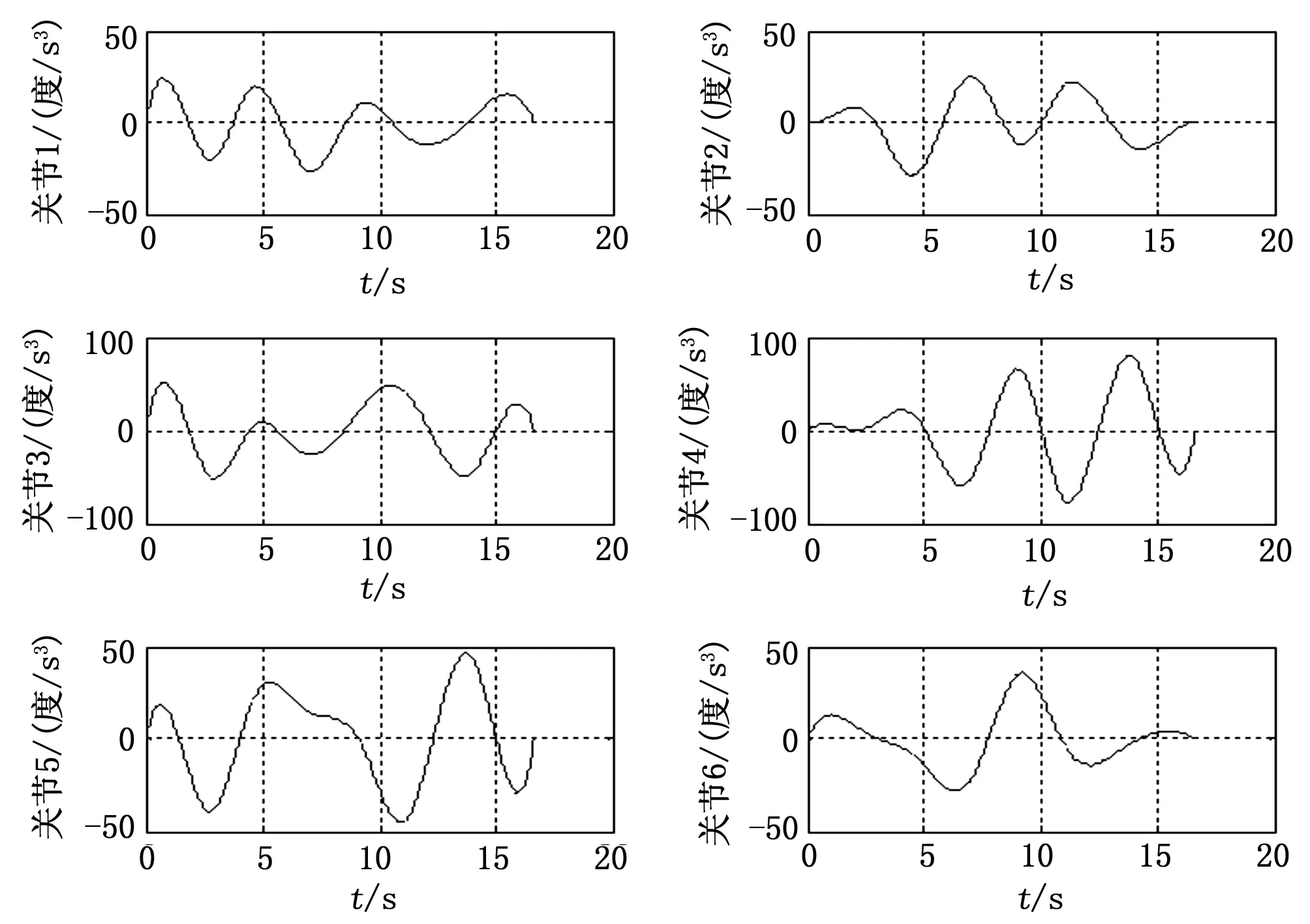
圖4 各關節角加速度曲線

圖5 各關節脈動曲線

由圖2可知根據上述算法所得的各關節軌跡均能通過設定的路徑點(“*”表示關節空間路徑點)；由圖3可知，各關節的角速度均在約束條件范圍內；由圖3、4可知，軌跡的啟停角速度、角加速度均為零；由圖4、5可知，得到的關節角加速度、角加加速度曲線均連續。

綜上，基于PSO算法的五次B樣條能得到運行時間較短、脈動連續且平均脈動較小的運動軌跡，確保了機器人較高的工作效率以及較高的平穩性。

運用正運動學計算出機器人執行器末端的軌跡，再利用MATLAB中的RobotToolbox可繪制出該機器人的三維模型，如圖6和圖7所示。

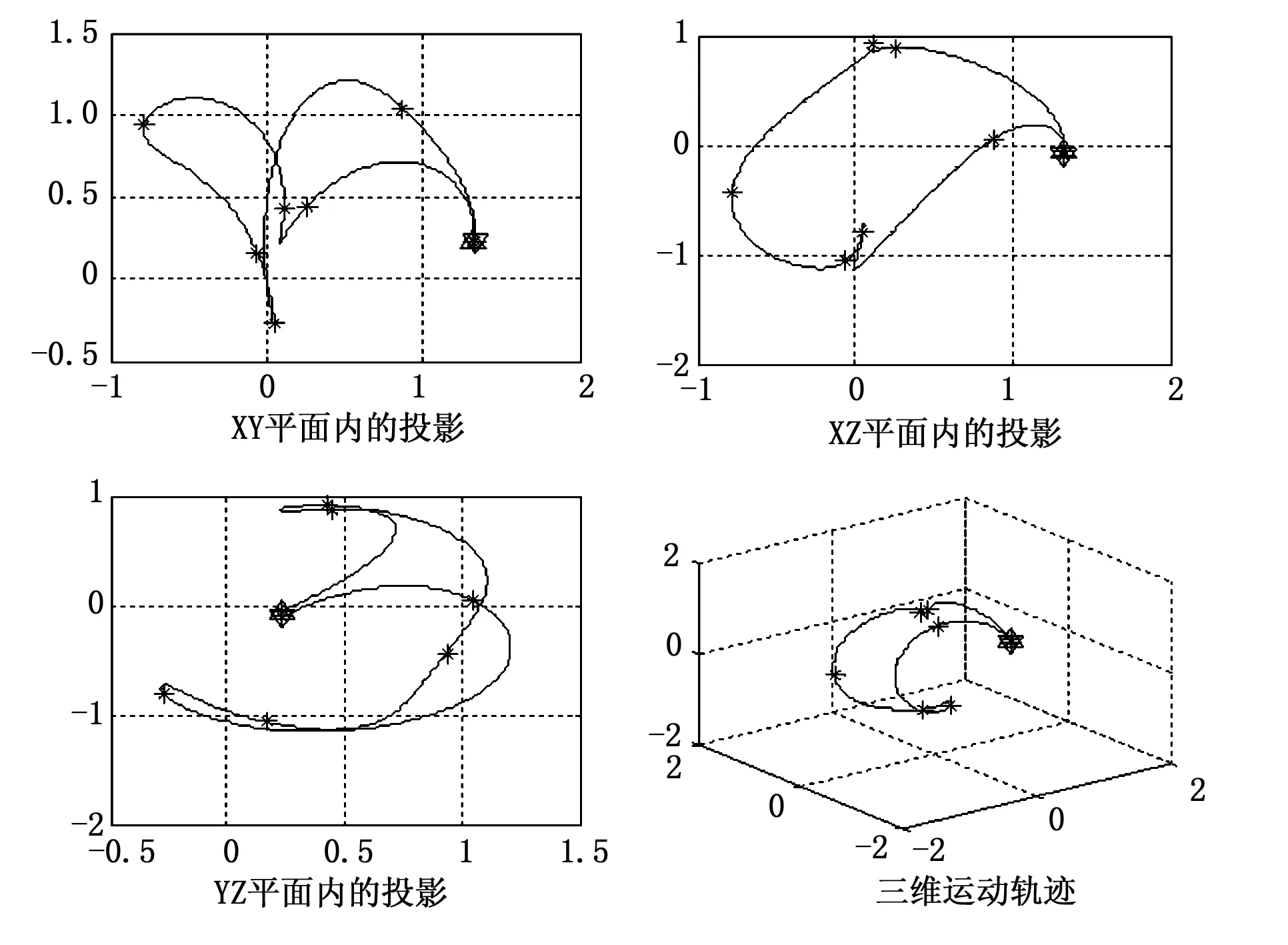
圖6 六自由度機器人執行器末端運動軌跡

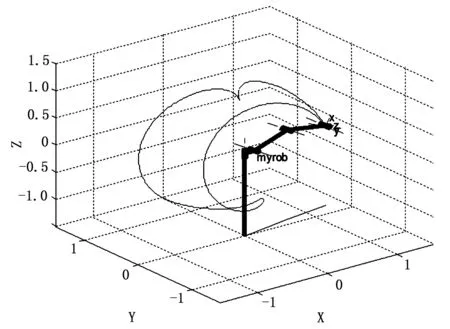
圖7 GRB4016工業機器人三維模型

圖6中，“＊”代表路徑點，“△”上三角代表起始點，“▽”下三角代表終止點，可看出，起止點基本重合。圖7為在MATLAB的RobotToolbox建立的GRB4016型號工業機器人的三維模型。

5 結論

本文運用了五次非均勻B樣條插值法，來進行關節空間的軌跡規劃，這種插值法相較于高階多項式插值法，具有凸包性和局部支撐性等優點。并通過PSO算法對規劃出的軌跡進行時間-脈動最優的優化。研究結果表明，本文提出的基于PSO優化算法的五次B樣條軌跡規劃方案，能夠得到時間-脈動較優的軌跡，實現了六自由度機器人較高的運行效率和平穩性的研究目標。

[1] 蔡自興.機器人學[M].北京:清華大學出版社,2000.

[2]JohnJ.Craig.機器人學導論[M].贠 超,等譯.北京：機械工業出版社,2006.

[3]LinCS,ChangPR,LuhJYS.Formulationandoptimizationofcubicpolynomialjointtrajectoriesforindustrialrobots[J].IEEETransactionsonAutomaticControl, 1984, 28(12): 1066-1074.

[4]Planningofmanipulatormotiontrajectorywithhigher-degreepolynomialsuse[J].MechanismandMachineTheory.2008,44(7):1400-1419.

[5] 王幼民.機械臂關節空間B樣條曲線軌跡規劃[J].安徽機電學院學報,2000,15(2):21-26.

[6] 田西勇.機器人軌跡規劃方法研究[D].北京:北京郵電大學,2008.

[7]ZhaXF.Optimalposetrajectoryplanningforrobotmanipulators[J].Mechanism&MachineTheory,2002,37(10):1063-1086.

[8] 徐海黎,解祥榮,莊 健,等.工業機器人的最優時間與最優能量軌跡規劃[J]. 機械工程學報,2010,46(9):19-25.

[9] 楊國軍,崔平遠.機械手時間最優軌跡規劃方法研究[J].中國機械工程,2002,13(20):1715-1717.

[10] 余 陽,林 明,林永才.基于混合遺傳算法的工業機器人最優軌跡規劃[J].計算機工程與設計,2012,33(4):1574-1580.

[11]GasparettoA,LanzuttiA,VidoniR,ZanottoV.Experimentalvalidationandcomparativeanalysisofoptimaltime-jerkalgorithmsfortrajectoryplanning[J].RoboticsandComputer-IntegratedManufacturing, 2012,28(2):164-181.

[12]GasparettoA,ZanottoV.Atechniquefortime-jerkoptimalplanningofrobottrajectories[J].RoboticsandComputer-IntegratedManufacturing, 2008,24(3):415-426.

[13]皮 格.非均勻有理B樣條[M].北京：清華大學出版社,2010.

[14]潘 峰.粒子群優化算法與多目標優化[M]. 北京:北京理工大學出版社,2013.

[15]高衛峰,劉三陽.一種高效粒子群優化算法[J].控制與決策.2011,26(8):1158-1162.

Time-jerk Optimal Trajectory Planning for Industrial Robots Based on PSO Algorithm

Shen Yue，Li Yinya，Qi Guoqing，Sheng Andong

(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

In order to improve the work efficiency and guarantee the joints’ smooth movement of industrial robots, this paper proposes a scheme of time-jerk optimal trajectory planning based on PSO(particle swarm optimization) algorithm. First, the multi-objective optimization is transformed into single-objective optimization by the approach of weighting. Then, the time-jerk optimal trajectory is obtained by using PSO algorithm. And the trajectory planning is fulfilled in joint space coordinate by quintic non-uniform B-spline interpolation, and which can guarantee the jerk curves’ continuity. Finally, this scheme is applied to GRB4016—an industrial robot. The simulation results show that this scheme can generate ideal trajectory, and demonstrate the effectiveness of the proposed scheme.

B-spline curve; PSO; time-jerk optimal; trajectory planning

2016-07-19；

2016-08-17。

國家自然科學基金資助項目(61273076)。

沈 悅(1991-)，女，江蘇南通人，碩士研究生，主要從事機器人方向的研究。

李銀伢(1976-)，男，江蘇南京人，副研究員，博士生導師，主要從事滿意待機控制、非線性估計理論及其工程應用方向的研究。

1671-4598(2017)01-0158-05DOI：10.16526/j.cnki.11-4762/tp

TP

A