有限域上多項式的指數(shù)和及其L-函數(shù)

韓山猛,祝美玲,曹煒

(寧波大學(xué)數(shù)學(xué)系,浙江 寧波 315211)

有限域上多項式的指數(shù)和及其L-函數(shù)

韓山猛,祝美玲,曹煒

(寧波大學(xué)數(shù)學(xué)系,浙江 寧波 315211)

L-函數(shù)蘊藏著深刻的算術(shù)信息,是數(shù)論中重要的研究對象.有限域上多項式的指數(shù)和及其L-函數(shù)在一般情形下難以計算.通過利用高斯和及多項式的次數(shù)矩陣的Smith標(biāo)準(zhǔn)形,得到了在特定情形下有限域上一類多項式的指數(shù)和及其L-函數(shù)的具體公式.

有限域;Smith標(biāo)準(zhǔn)形;指數(shù)和;L-函數(shù)

1 引言

用 Fq表示特征為p的q元有限域,F?q為其乘法群.對給定的正整數(shù) r,用表示Fq的 r次擴域.設(shè) f是 Fq上的 n元 d次多項式,用 Nq(f)和 Nq?(f)分別表示方程 f=0在Fq和F?q中的解的個數(shù).由于在一般情形下要給出Nq(f)和Nq?(f)的具體表達式是困難的,研究者們努力尋找它們在特定情形下的表達式或某種形式的估計;參見文獻 [1-3].著名的Chevalley-Warning定理給出了Nq(f)的p-adic估計:若n＞d,則p|Nq(f).Ax[4]改進了該定理,他證明了,其中為不小于x的最小整數(shù),ordq是q進制加法賦值,且滿足ordqq=1.2005年,王文松和孫琦[5]得到了一類三角方程

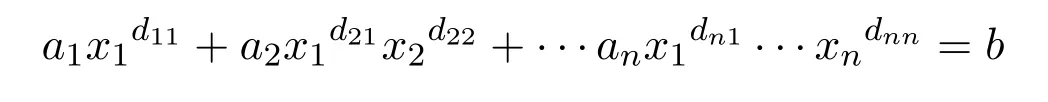
在gcd(d11d22…dnn,q?1)=1條件下的解數(shù)公式.2007年,曹煒和孫琦[6]發(fā)現(xiàn)如果多項式f的次數(shù)矩陣非奇異,則可給出Nq(f)的具體表達式.2009年,曹煒[7]通過Smith標(biāo)準(zhǔn)形將文獻[6]中的結(jié)果推廣到了增廣次數(shù)矩陣上.2013年,陳建明和曹煒[8]利用Smith標(biāo)準(zhǔn)形給出了Nq?(f)的一個估計.

2 預(yù)備知識

定義 1.1設(shè)

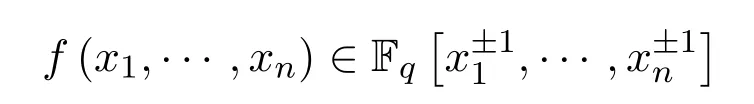
是一個洛朗多項式,定義指數(shù)和:

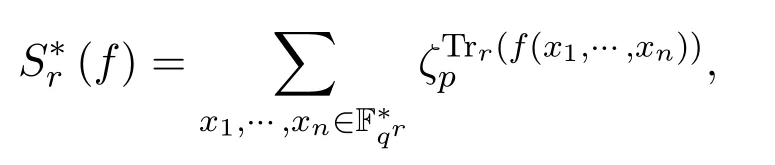
其對應(yīng)的L-函數(shù)定義如下:

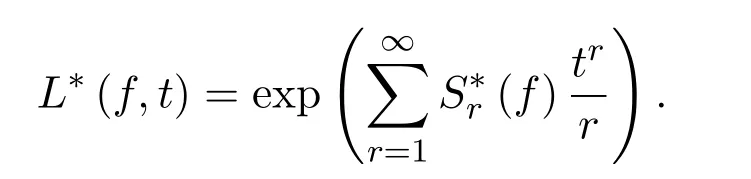
從定義1.1中可以看到,S?r(f)和L?(f,t)中的f可以是洛朗多項式,即其變量的次數(shù)可以為負整數(shù).但為了敘述的統(tǒng)一,下文中均討論f為多項式的情形;須注意的是,關(guān)于S?r(f)和L?(f,t)的結(jié)果均可推廣到洛朗多項式上.

定義 1.2設(shè)

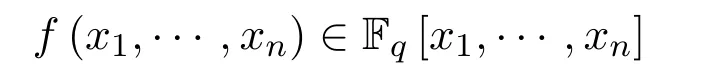
是一個多項式,定義指數(shù)和:

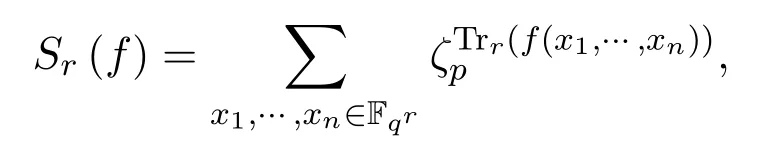
其對應(yīng)的L-函數(shù)定義如下:

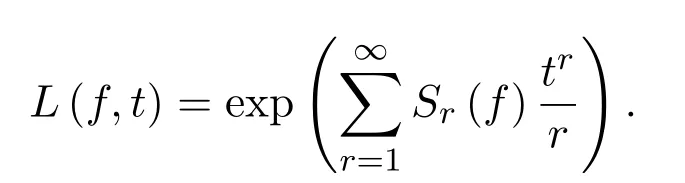
由Dwork-Bombieri-Grothendieck定理知,L?(f,t)是有理函數(shù),即

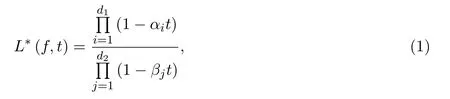
其中有限多個零點αi(1≤i≤d1)和極點βj(1≤j≤d2)是非零的代數(shù)整數(shù).等價地,對每個正整數(shù)r,均有以下公式:

對于指數(shù)和Sr(f)及其相應(yīng)的L-函數(shù)L(f,t),亦有類似的結(jié)論,不再贅述.下面將會發(fā)現(xiàn),相對而言計算S?r(f)和L?(f,t)比計算Sr(f)和L(f,t)更容易些.

下面介紹多項式的次數(shù)矩陣及Smith標(biāo)準(zhǔn)形的相關(guān)概念,它是本文研究指數(shù)和及其L-函數(shù)的重要工具.

定義 1.3假設(shè)f(x1,…,xn)∈Fq[x1,…,xn]有如下稀疏表達式:

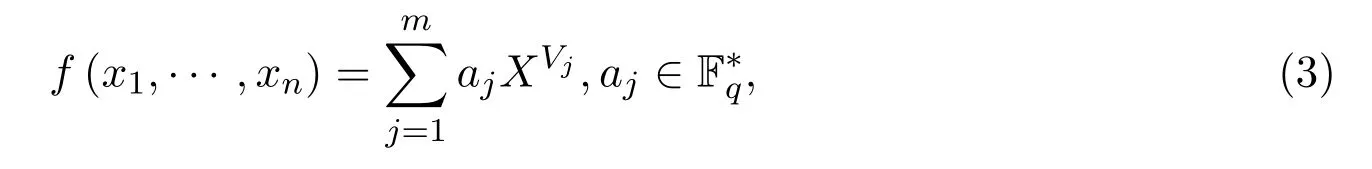
對于任意的環(huán)R,用GLn(R)表示R上階為n的一般線性群,即R上所有n×n階可逆方陣關(guān)于矩陣乘法構(gòu)成的群.特別地,當(dāng)R=?時,GLn(?)里的元稱為幺模矩陣.當(dāng)我們考慮f∈Fq[x1,...,xn]的次數(shù)矩陣D時,由于對任意的α∈Fq,有αq=α,因此不妨將其看成是剩余類環(huán) ?q?1上的一個矩陣.若D在?q?1上可逆,則記為D∈GLn(?q?1).如無特別提示,下文中出現(xiàn)的f和D均指定義1.3中的f和D.

引理1.1[10]設(shè)A∈?n×m的秩為k,則存在兩個幺模矩陣H∈GLn(?)和K∈GLm(?),使得A等價于HAK=(λij),其中λij=0若i≠j,對角元λi:=λii滿足:λi|λi+1,λi＞0,這里1≤i≤k?1,且λk＞0.

上面引理1.1中的λi(1≤i≤k)由A唯一確定,稱為A的第i個不變因子,HAK 稱為A的Smith標(biāo)準(zhǔn)形,記作SNF(A).

引理1.2[7]設(shè)A為整數(shù)矩陣.則同余式方程組AX=0的整數(shù)解和SNF(A)Y=0的整數(shù)解之間存在一一對應(yīng)的關(guān)系.特別地,AX=0只有零解當(dāng)且僅當(dāng)SNF(A)Y=0只有零解.

引理 1.3[7]DX≡0(mod qr?1)只有零解當(dāng)且僅當(dāng)

只有零解.

3 S?r(f)和 L?(f,t)的計算

本節(jié)將要用到Teichm¨uller特征與高斯和,詳細介紹參見文獻[9-12].回憶上一節(jié)中固定ζp為一個復(fù)本原單位根,Trr表示從Fqr到素域Fp的絕對跡映射.設(shè)ω是的Teichm¨uller特征,對于是(qr?1)次復(fù)單位根.因ω的階為(qr?1),故的所有乘法特征可由ω生成.定義上的(qr?1)個高斯和

定理 2.1假設(shè) D ∈?n×m(m≤n),r為給定的正整數(shù).若 SNF(D)的不變因子為λ1≤…≤λm且滿足gcd(λm,qr?1)=1,則有

推論 2.1 假設(shè) D ∈?n×m(m≤n),r為給定的正整數(shù).若 D 有一個 m 階子方陣M∈GLm(?qr?1),則有

證明由題設(shè),此時D的最大不變因子為第m個且它與qr?1互素.應(yīng)用定理2.1即得.

定理 2.2假設(shè)D∈?n×m(m≤n).若SNF(D)的不變因子為λ1≤…≤λm,且對所有的正整數(shù)r,均有

則有

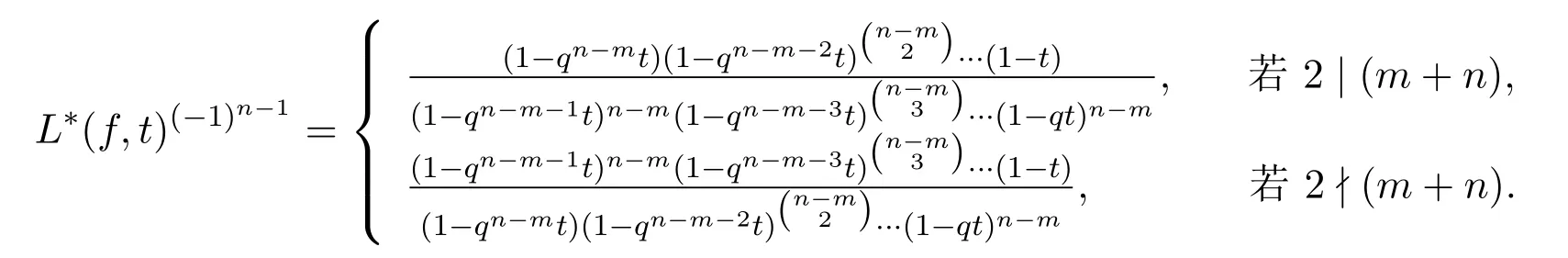
下面我們給出定理2.2中L?(f,t)另一種更為緊湊的表達式.它需要用到下面這個引理.

引理 2.1若

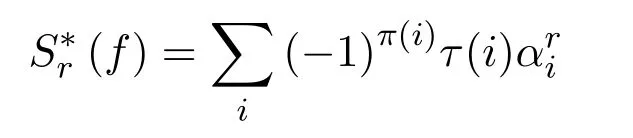
對所有的正整數(shù)r都成立,其中π(i)和τ(i)是取值于非負整數(shù)的數(shù)論函數(shù),則有

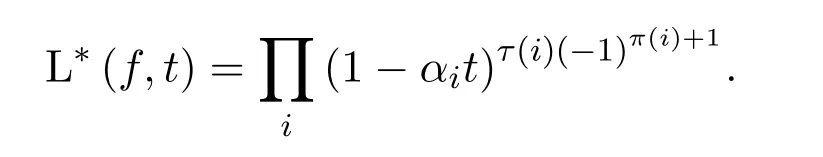
證明由(1)和(2)即可證得.

定理 2.3假設(shè)D∈?n×m(m≤n).若SNF(D)的不變因子為λ1≤…≤λm,且對所有的正整數(shù)r,均有g(shù)cd(λm,qr?1)=1.則有

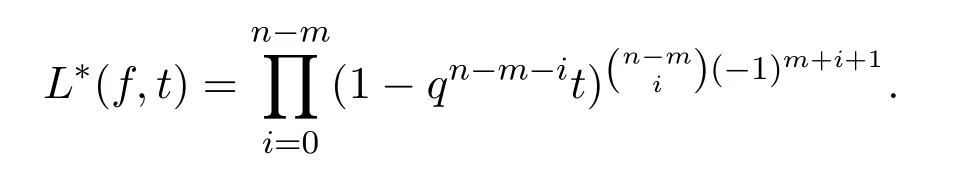
證明注意此時有

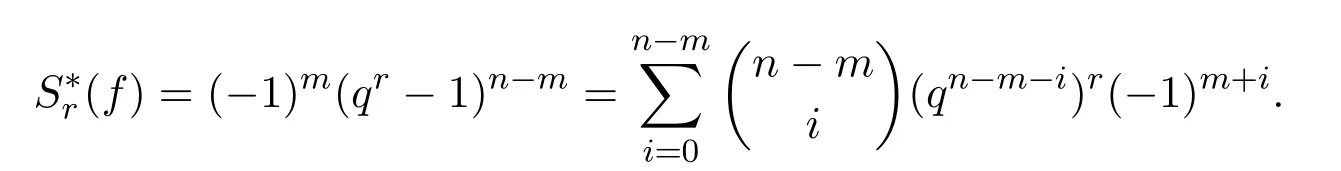
應(yīng)用引理2.1即可得.

注 2.1定理 2.2中 L?(f,t)(?1)n?1的表達式并非沒有意義.事實上,在一些特殊情形下, L?(f,t)(?1)n?1比L?(f,t)具有更好的性質(zhì),因而有不少研究前者的文獻（如[10,13-14]等）.

推論2.2假設(shè)D∈?n×m(m≤n).若SNF(D)的不變因子為λ1=…=λm=1,則有

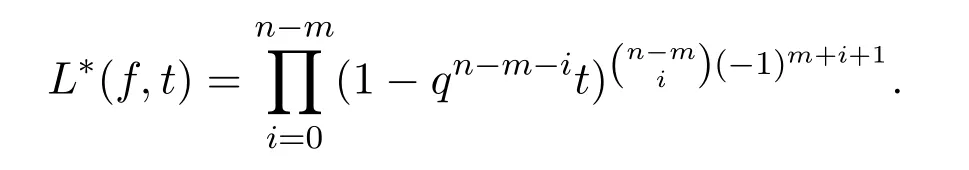
4 Sr(f)和 L(f,t)的計算

本節(jié)討論Sr(f)和L(f,t)的計算.類似于前一節(jié)的討論,定義Fqr上的(qr?2)個高斯和

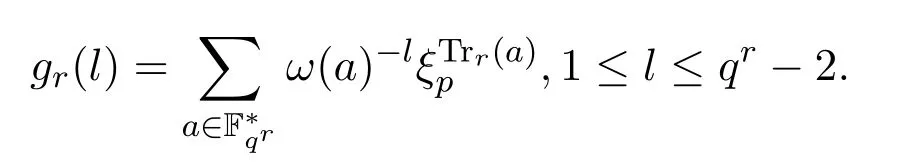
令

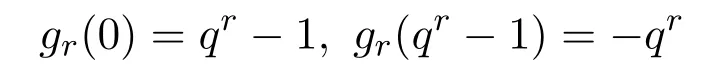
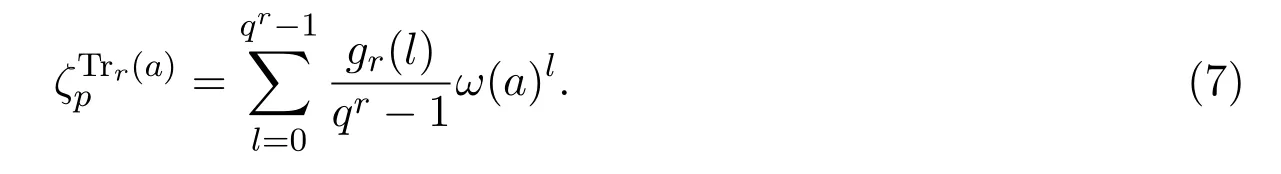
由特征的正交性質(zhì)(5),有

令

及

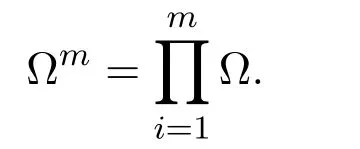
對于給定的一個向量l=(l1,…,lm)∈?m,令

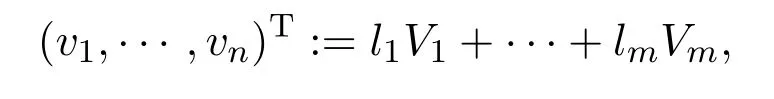
并用σ(l)和s(l)分別表示向量(l1,…,lm)和(v1,…,vn)中非零元的個數(shù).由(7)和(8),我們計算得

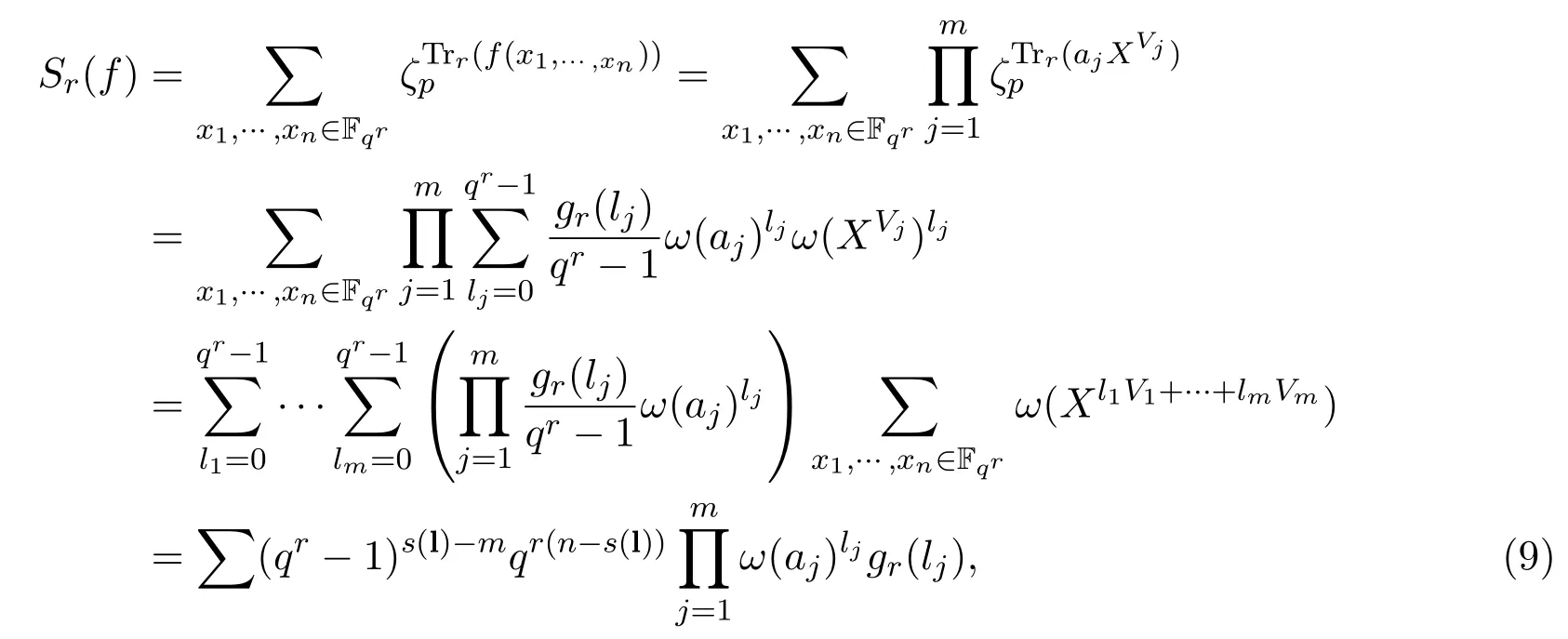
其中和號遍歷所有的向量l=(l1,…,lm)∈?m,且滿足

注意到gr(0)=qr?1,gr(qr?1)=?qr及對任意的aj∈F?q,有ω(aj)0=1,類似于上一節(jié)定理2.1和定理2.3的證明,可得以下結(jié)論:

定理 3.1假設(shè)D∈?n×m(m≤n),且SNF(D)的不變因子為λ1≤…≤λm.若對某個正整數(shù)r有g(shù)cd(λm,qr?1)=1,則有

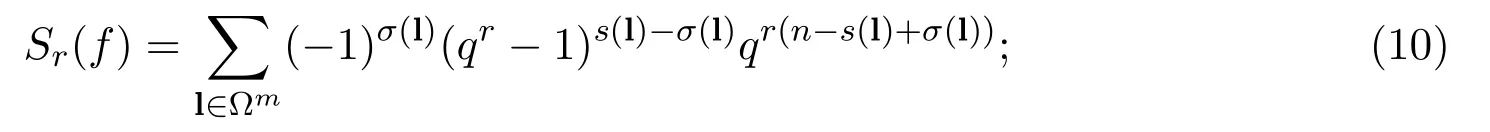
若對所有的正整數(shù)r均有g(shù)cd(λm,qr?1)=1,則有

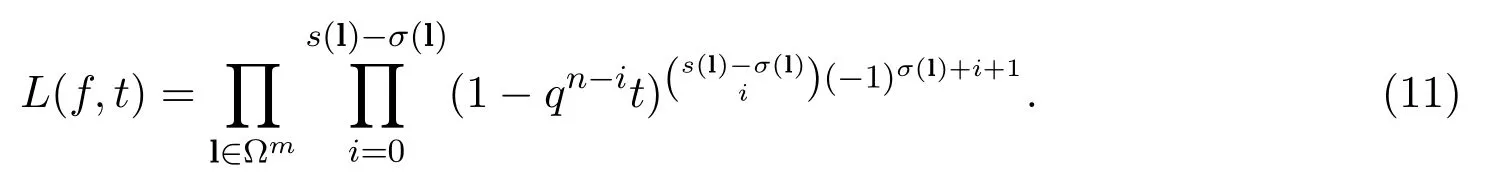
推論 3.1假設(shè)D∈?n×m(m≤n).若對某個正整數(shù)r,D存在一個m階子方陣M∈GLm(?qr?1),則(10)成立;若對任意的正整數(shù)r,D均有一個m階子方陣M∈GLm(?qr?1),則(11)成立.

5 例子

在最后一節(jié)給出一個簡單的例子,說明如何應(yīng)用前兩節(jié)中的結(jié)論計算S?r(f),L?(f,t),Sr(f)及L(f,t),并利用指數(shù)和與有理點個數(shù)之間的關(guān)系,給出Nq(f)和Nq?(f)的具體值.設(shè)多項式

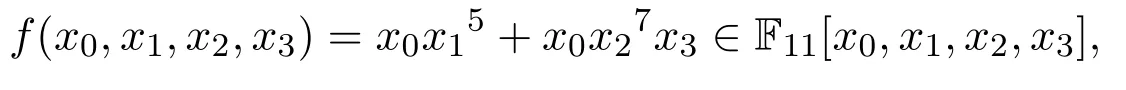
則f的次數(shù)矩陣為:

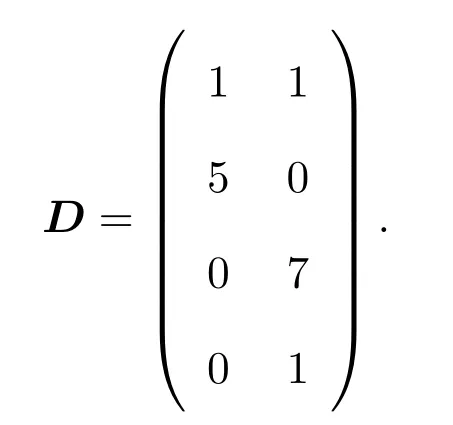
顯見,D中由第一行和最后一行組成的2階子方陣M是幺模矩陣,故對于所有正整數(shù)r,均有M∈GL2(?/(11r?1)).同余式方程組

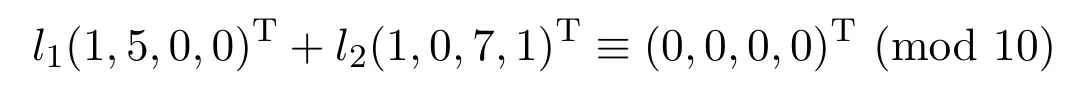
的每個解l=(l1,l2)9A?σ(l)與s(l)值見表1.

No.l=(l1,l2)σ(l)s(l) 1 (0,0) 0 0 2 (0,10) 1 3 3 (10,0) 1 2 4 (10,10) 2 4

這里q=11,n=4,m=2,?={0,10}.利用定理 2.1,定理 2.3和定理 3.1分別計算及L(f,t)可得:

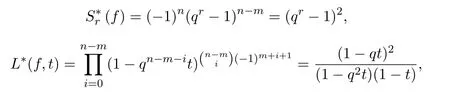
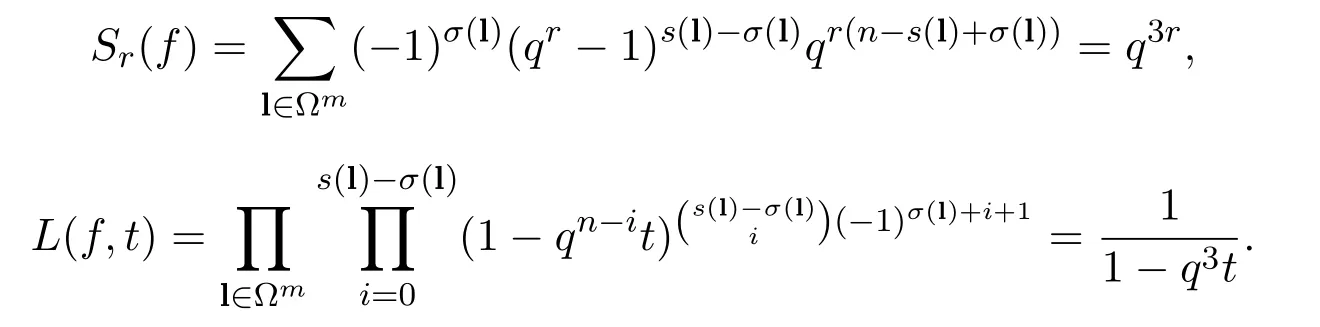
下面考察多項式

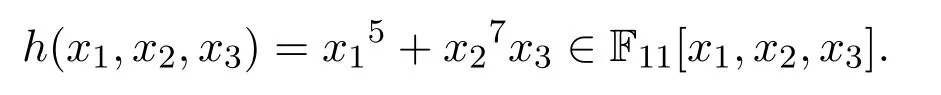
顯見,

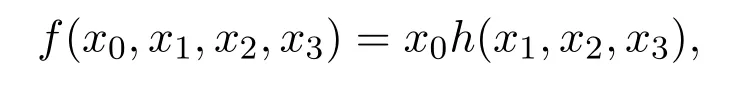
其中x0是作為一個新變量出現(xiàn)的.由解數(shù)與指數(shù)和的關(guān)系可得:

通過 Maple編程,易計算出多項式 h(x1,x2,x3)的 Fq-有理點個數(shù)為 121,有理點個數(shù)為100,與上述結(jié)果完全相符.

[1]馮克勤,廖群英.有限域及其應(yīng)用[M].大連:大連理工大學(xué)出版社,2011.

[2]Lidl R,Niederreiter H.Finite Fields[M].Cambridge UK:Cambridge Univ Press,1997.

[3]Schmidt W M.Equations over Finite Fields:An Elementary Approach[M].New York:Springer-Verlag, 1976.

[4]Ax J.Zeros of polynomials over fi nite fi elds[J].Amer J Math.,1964,2:255-261.

[5]Wang W S,Sun Q.The number of solutions of certain equations over fi nite fi elds[J].Finite Fields Appl., 2005,2:182-192.

[6]Cao W,Sun Q.On a class of equations with special degrees over fi nite fi elds[J].Acta Arith.,2007,130:195-202.

[7]Cao W.Smith normal form of augmented degree matrix and its applications[J].Linear Algebra Appl., 2009,431:1778-1784.

[8]Chen J M,Cao W.Smith normal form of augmented degree matrix and rational points on toric hypersurface[J].Algebra Colloq.,2013,20:327-332.

[9]Hong S F.L-functions of twisted diagonal exponential sums over fi nite fi elds[J].Proc.Amer.Math.Soc., 2007,135:3099-3108.

[10]Smith J S.On systems of linear indeterminate equations and congruences[J].Philos.Trans.Royal.Soc.London,1861,151:293-326.

[11]Berndt B,Evans R,Williams K.Gauss and Jacobi Sums[M].New Yock:Wiley Interscience,1998.

[12]陳國華,武艷麗,張艷娜.某種特定類型三角和的定量估計[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2013,29:325-330.

[13]Adolphson A,Sperber S.Exponential sums and Newton polyhedra:cohomology and estimates[J].Ann.Math., 1989,130:367-406.

[14]Adolphson A,Sperber S.Newton polyhedra and the degree of the L-function associated to an exponential sum[J].Invent Math.,1987,88:555-569.

Exponential sums and L-functions of polynomials over fi nite fi elds

Han Shanmeng,Zhu Meiling,Cao Wei
(Department of Mathematics,Ningbo University,Ningbo 315211,China)

L-functions contains rich information of arithmetic and are an important study object in number theory.In general it is difficult to compute the exponential sums and the corresponding L-functions of the polynomials over fi nite fi elds.Using Gauss sums and the Smith normal form of the degree matrix for polynomials over fi nite fi elds,we obtain the explicit formulas for the exponential sums and the corresponding L-functions of polynomials over fi nite fi elds under certain conditions.

fi nite fi eld,Smith normal form,exponential sum,L-function

O156

A

1008-5513(2017)01-0092-10

10.3969/j.issn.1008-5513.2017.01.0010

2017-01-18.

國家自然科學(xué)基金(11371208);寧波市自然科學(xué)基金(2016A610079).

韓山猛(1991-),碩士生,研究方向：數(shù)論、有限域及其應(yīng)用.

2010 MSC:11M06